Parametric Surfaces We can use parametric equations to








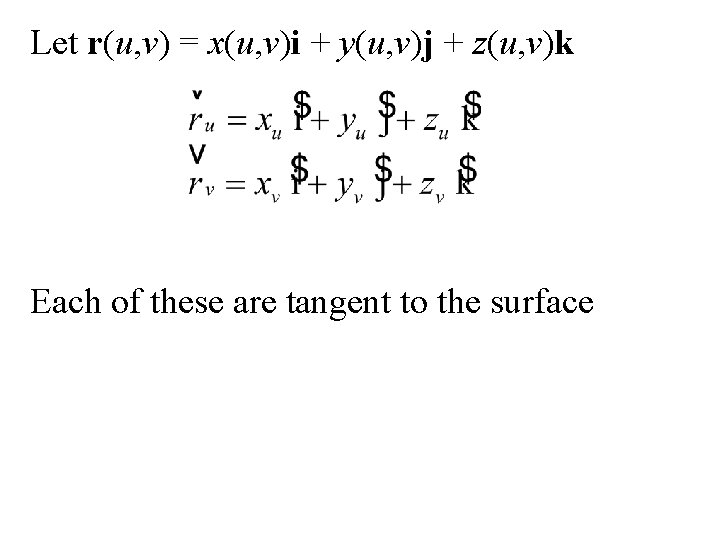







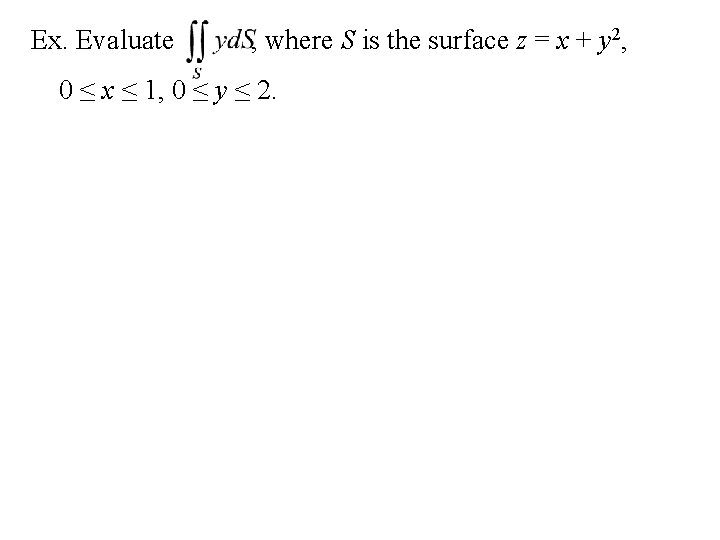


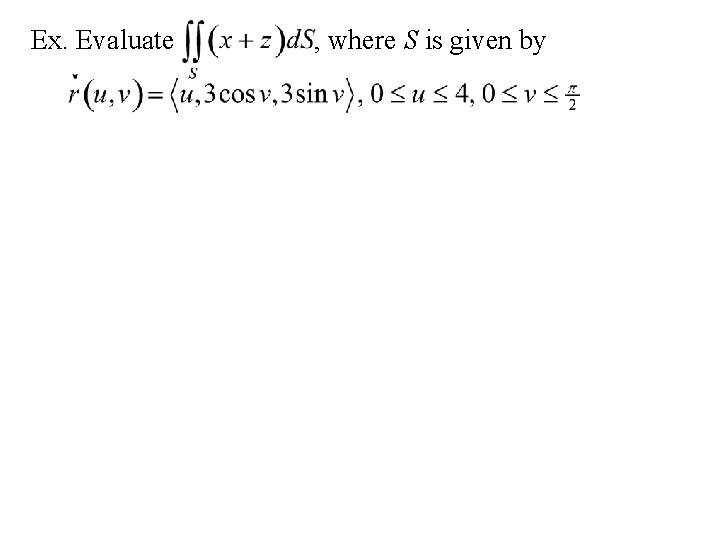





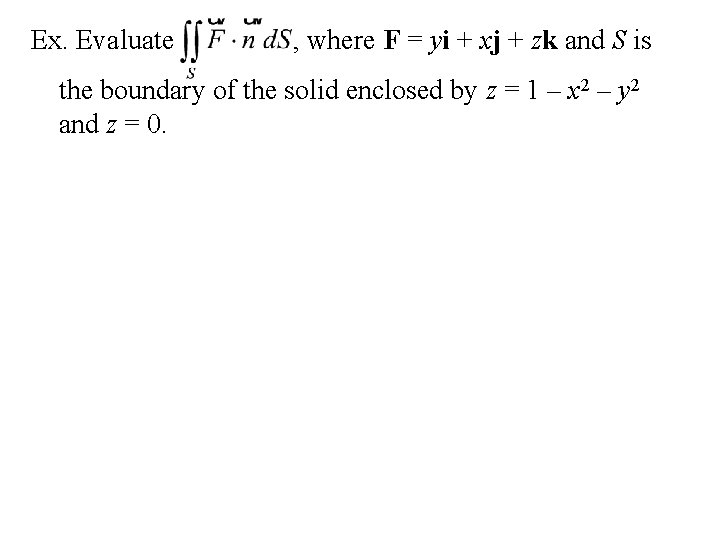


- Slides: 28

Parametric Surfaces We can use parametric equations to describe a curve. Because a curve is one dimensional, we only need one parameter. If we want to describe a surface (two dimensions) using parametric equations, we will need two parameters. r(u, v) where the domain refers to values in the uv-plane.

Ex. Identify the surface with vector equation r(u, v) = 2 cos ui + vj + 2 sin uk.

Ex. Identify the surface with vector equation r(u, v) = 5 ui + (2 u + v)j + v 2 k.

Ex. Find the rectangular equation of the surface with vector equation r(u, v) = 2 ucos vi + ½u 2 j + 2 usin vk.

Ex. Find a parametric representation of the sphere x 2 + y 2 + z 2 = a 2.

Ex. Find a parametric representation of the elliptic paraboloid z = 2 x 2 + y 2.

For surfaces created by rotating the function y = f (x) about the x-axis, the parametric equations would be x=u y = f (u) cos v z = f (u) sin v These can be adapted for rotation around the y- or z-axis.

Ex. Find the parametric equation of the surface generated by rotating z = ln y about the y-axis.
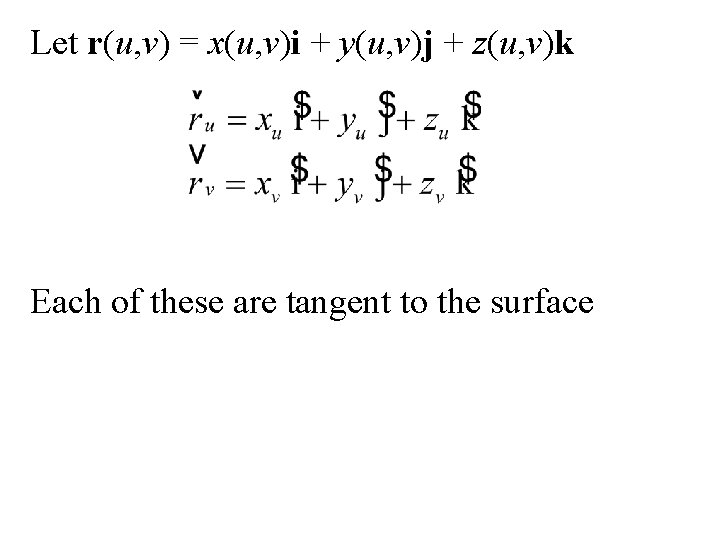
Let r(u, v) = x(u, v)i + y(u, v)j + z(u, v)k Each of these are tangent to the surface

Ex. Find the equation of the plane tangent to the surface r(u, v) = u 2 i + v 2 j + (u + 2 v)k at the point (1, 1, 1).

Thm. If a surface S is defined by the vector function r(u, v), defined on the region D in the uv-plane, then the surface area of S is

Ex. Find the surface area of the sphere of radius a.

Ex. Find the area of the surface defined by z = f (x, y).

Ex. Find the area of the part of the paraboloid z = x 2 + y 2 that lies under the plane z = 9.

Surface Integrals Line integrals added the values of a function at every point on a curve. Surface integrals add the value of a 3 -D function at every point on a surface.

Let S be a surface with equation z = g(x, y), and let R be the projection of S onto the xy -plane.
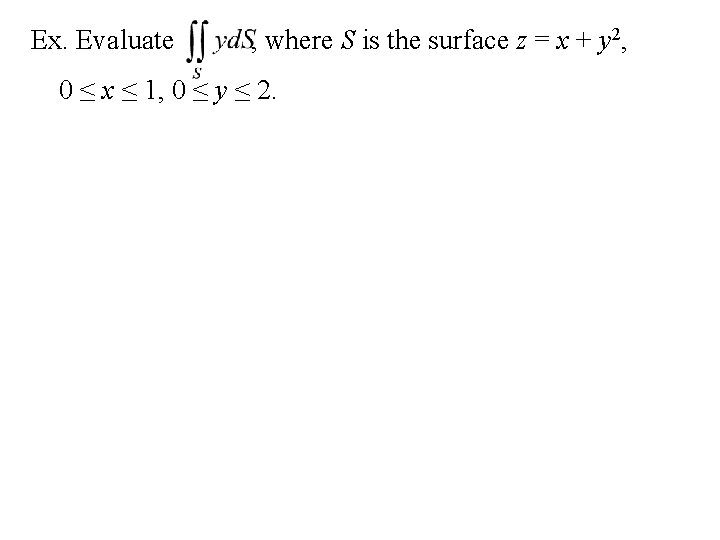
Ex. Evaluate , where S is the surface z = x + y 2, 0 ≤ x ≤ 1, 0 ≤ y ≤ 2.

Ex. Evaluate , where S is the first octant portion of 2 x + y + 2 z = 6.

If the surface can not be written as z = g(x, y), then we need to parameterize it like last time. Thm. If S can be represented parametrically by , then where D is the domain in the uv-plane.
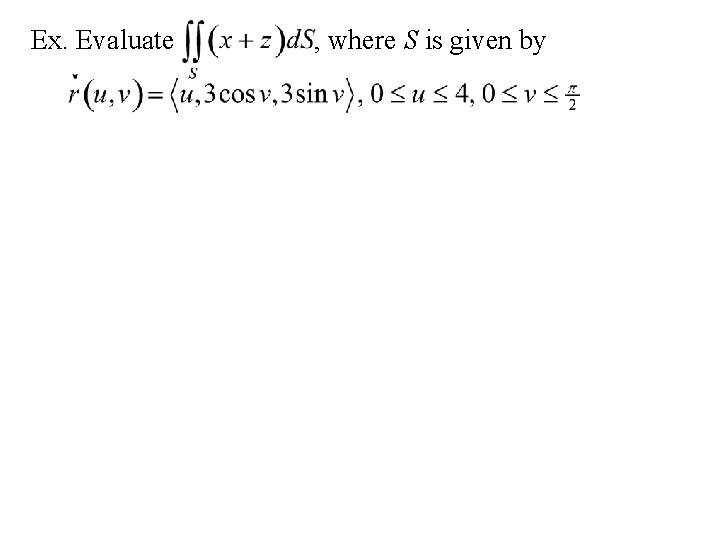
Ex. Evaluate , where S is given by

Ex. Evaluate , where S is the unit sphere.

Ex. Evaluate , where S is the surface of the region bounded by x 2 + y 2 = 1, z = 0, and z = 1 + x.


Surface Integrals of Vector Fields Let S be an oriented surface with unit normal vector n. The surface integral of F over S is also called the flux integral of F over S. If F is a force causing energy to flow through our surface, the flux integral gives the rate of flow through S.

For surface defined by z = g(x, y), the unit normal vector is
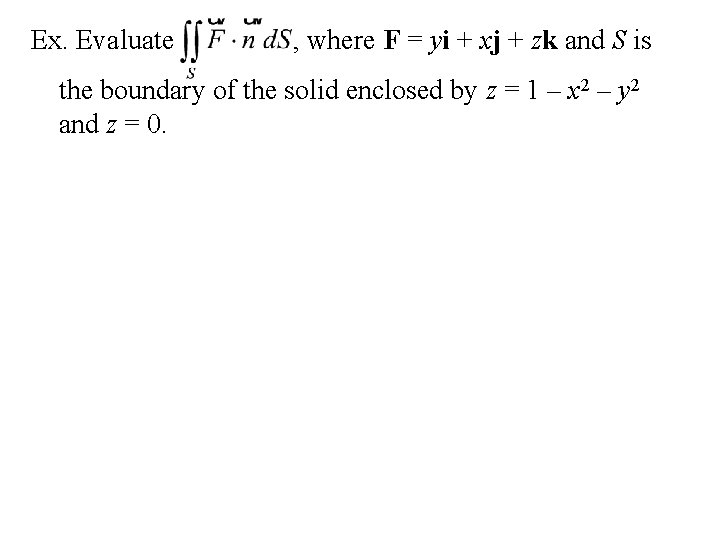
Ex. Evaluate , where F = yi + xj + zk and S is the boundary of the solid enclosed by z = 1 – x 2 – y 2 and z = 0.

For a surface that is defined parametrically, the unit normal vector is

Ex. Find the flux of the vector field F = zi + yj + xk across the unit sphere.