Parametric Polymorphism Antonio Cisternino Giuseppe Attardi Universit di

Parametric Polymorphism Antonio Cisternino Giuseppe Attardi Università di Pisa

Parametric Polymorphism l l l C++ templates implement a form of parametric polymorphism PP is implemented in many flavors and many languages: Eiffel, Mercury, Haskell, ADA, ML, C++, … Improve the expressivity of a language May improve the performance of programs It is a form of Universal polymorphism

C++ templates and macros l l Macros are dealt by the preprocessor C++ templates are implemented on the syntax tree The instantiation strategy is lazy The following class compiles unless the method foo is used: template <class T>class Foo { T x; int foo() { return x + 2; } }; Foo<char*> f; f. x = “”; f. foo();

A more semantic approach l Parametric polymorphism has been introduced also in Java and C# § Java Generics and Generic C# for. NET In both cases the compiler is able to check parametric classes just looking at their definition l Parametric types are more than macros on AST l Syntax for generics is similar l

Generics in a Nutshell l Type parameterization for classes, interfaces, and methods e. g. In GJ is class Set<T>. . . } // parameterized class <T> T[]{ Slice(…) class Dict<K, D> {. . . } // two-parameter class interface IComparable<T> {. . . } // parameterized interface struct Pair<A, B> {. . . } // parameterized struct (“value class”) T[] Slice<T>(T[] arr, int start, int count) // generic method l Very few restrictions on usage: • Type instantiations can be primitive (only C#) or class e. g. Set<int> Dict<string, List<float>> Pair<Date. Time, My. Class> • Generic methods of all kinds (static, instance, virtual) • Inheritance through instantiated types e. g. class Set<T> : IEnumerable<T> class Fast. Int. Set : Set<int> Virtual methods only in GC#!

More on generic methods l l Generic methods are similar to template methods in C++ As in C++ JG tries to infer the type parameters from the method invocation C# requires specifying the type arguments Example: template <class T> T sqr(T x) { return x*x; } std: : cout << sqr(2. 0) << std: : endl; C++ class F { <T> static void sort(T[] a) {…} } String[] s; F. sort(s); JG class F { static void sort<T>(T[] a) {…} } string[] s; F. sort<string>(s); C#

Generic Stack class Stack<T> { private T[] items; How does private int nitems; the compiler Stack<T>() { nitems = 0; items = new T[] (50); } check the T Pop() { definition? if (nitems == 0) throw Empty(); return items[--nitems]; } bool Is. Empty() { return (nitems == 0); } void Push(T item){ if (items. Length == nitems) { T[] temp = items; items = new T[nitems*2]; Array. Copy(temp, items, nitems); } items[nitems++] = item; } }

The semantic problem The C++ compiler cannot make assumptions about type parameters l The only way to type-check a C++ class is to wait for argument specification (instantiation): only then it is possible to check operations used (i. e. comp method in sorting) l From the standpoint of the C++ compiler semantic module all types are not parametric l

Checking class definition l l l To be able to type-check a parametric class just looking at its definition the notion of bound is introduced Like method arguments have a type, type arguments are bound to other types The compiler will allow to use values of such types as if upcasted to the bound type Example: class Vector<T: Sortable> Elements of the vector should implement (or inherit from) Sortable

Example interface Sortable<T> { int compare. To(T a); } class Vector<T: Sortable<T>> { T[] v; int sz; Vector() { sz = 0; v = new T[15]; } Not possible in Java, void add. Element(T e) {…} because Sortable is an void sort() { interface and type T is lost. … if (v[i]. compare. To(v[j]) > 0) … } } Compiler can typecheck this because v contains values that implement Sortable<T>

Pros and Cons A parameterized type is checked also if no instantiation is present l Assumptions on type parameters are always explicit (if no bound is specified Object is assumed) l Is it possible to make assumptions beyond bound? l Yes, you can always cheat by upcasting to Object and then do whatever you want: l class Foo<T : Button> { void foo(T b) { String s = (String)(Object)b; } } l Still the assumption made by the programmer is explicit

Implementation l Different implementations of parametric polymorphism: § C++ only collects definition at class definition; code is produced at first instantiation § Java deals with generic types at compile time: the JVM is not aware of parametric types § C# exploits support by the CLR (Common Language Runtime) of parametric types • the CIL (Common Intermediate Language) has special instructions for dealing with type parameters

Java Generics strategy The Java compiler verifies that generic types are used correctly l Type parameters are dropped and the bound is used instead; downcasts are inserted in the right places l Generated code is a normal class file unaware of parametric polymorphism l

Example class Vector<T> { T[] v; int sz; Vector() { v = new T[15]; sz = 0; } <U implements Comparer<T>> void sort(U c) { … c. compare(v[i], v[j]); … } } … Vector<Button> v; v. add. Element(new Button()); Button b = v. element. At(0); class Vector { Object[] v; int sz; Vector() { v = new Object[15]; sz = 0; } void sort(Comparer c) { … c. compare(v[i], v[j]); … } } … Vector v; v. add. Element(new Button()); Button b = (Button)b. element. At(0);

Wildcard class Pair<X, Y> { X first; Y second; } public String pair. String(Pair<? , ? > p) { return p. first + “, “ + p. second; }

Expressivity vs. efficiency l l l JG does not improve execution speed; though it helps to express genericity better than inheritance Major limitation in JG expressivity: exact type information is lost at runtime All instantiations of a generic type collapse to the same class Consequences are: no virtual generic methods and pathological situations Benefit: old Java < 5 classes could be seen as generic types! Reuse of the existing codebase

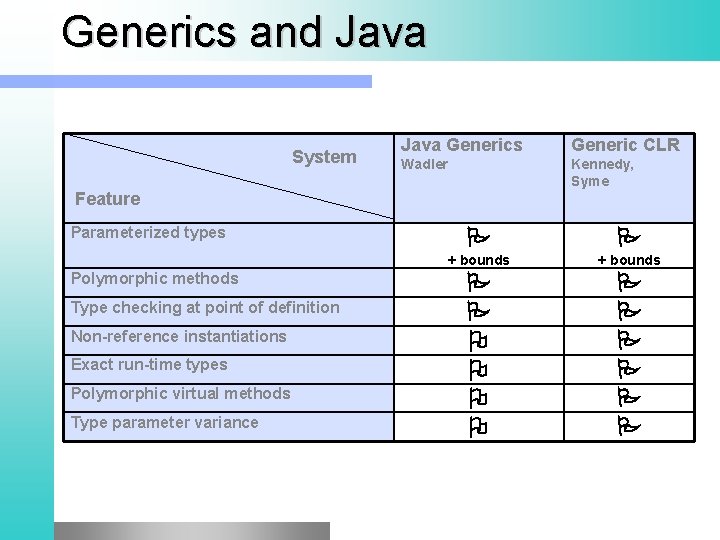
Generics and Java System Java Generics Generic CLR Wadler Kennedy, Syme Feature Parameterized types Polymorphic methods Type checking at point of definition Non-reference instantiations Exact run-time types Polymorphic virtual methods Type parameter variance + bounds

Compilation Strategies l Java compiler compiles to Java bytecode: § Java bytecode is loaded and compiled at run time by the JIT + Hot. Spot l C# (and other CLR) compilers generate CIL code which is compiled to binary at load time

Problem with Java Generics Stack<String> s = new Stack<String>(); s. push("Hello"); Stack<Object> o = s; Stack<Button> b = (Stack<Button>)o; // Class cast exception Button mb = b. pop(); Cast authorized: both Stack<String> and Stack<Button> map to class Stack

Type Erasure Array. List<Integer> li = new Array. List<Integer>(); Array. List<Float> lf = new Array. List<Float>(); if (li. get. Class() == lf. get. Class()) { // evaluates to true System. out. println("Equal"); }

Generic C# The CLR supports parametric types l In IL placeholders are used to indicate type arguments (!0, !1, …) l When the program needs an instantiation of a generic type the loader generates the appropriate type l The JIT can share implementation of reference instantiations (Stack<String> has essentially the same code of Stack<Object>) l

Generic C# compiler l l l Template-like syntax with notation for bounds NO type-inference on generic methods: the type must be specified in the call The compiler relies on GCLR to generate the code Exact runtime types are granted by the CLR so virtual generic methods are allowed All type constructors can be parameterized: struct, classes, interfaces and delegates.

Example using System; namespace n { public class Foo<T> { T[] v; Foo() { v = new T[15]; } public static void Main(string[] args) { Foo<string> f = new Foo<string>(); f. v[0] = "Hello"; string h = f. v[0]; Console. Write(h); } } } . field private !0[] v. method private hidebysig specialname rtspecialname instance void . ctor() cil managed { . maxstack 2 ldarg. 0 call instance void [mscorlib]System. Object: : . ct or() ldarg. 0 ldc. i 4. s 15 newarr !0 stfld !0[] class n. Foo<!0>: : v ret } // end of method Foo: : . ctor

Performance of CLR Generics Despite instantiation being performed at load time, the overhead is minimal l Code sharing reduces instantiations, improving execution speed l A technique based on dictionaries is employed to keep track of previous instantiated types l

Expressive power of Generics l l System F is a typed -calculus with polymorphic types While Turing-equivalence is a trivial property of programming languages, for a type-system being equivalent to System F it is not Polymorphic languages such as ML and Haskell cannot fully express System F (both languages have been extended to fill the gap) System F can be transposed into C# http: //www. cs. kun. nl/~erikpoll/ftfjp/2002/Kenn edy. Syme. pdf

Liskov Substitution Principle l Sub-Typing/Sub-Classing defines the class relation “B is a sub-type of A”, marked B <: A. According to the substitution principle, if B <: A, then an instance of B can be substituted for an instance of A. l Therefore, it is legal to assign an instance b of B to a variable of type A l A a = b;

Inheritance as Subtyping l Simple assumption: § If class B derives from class A then: B <: A

Generics and Subtyping l Do the rules for sub-types and assignment work for generics? If B <: A, then G<B> <: G<A>? Counter example List<String> ls = new List<String>(); List<Object> lo = ls; // Since String <: Object, so far so good. lo. add(new Object()); String s = (String)ls. get(0); // Error! The rule B <: A G<B> <: G<A> defies the principle of substitution!

Other example class B extends A { … } class G<E> { public E e; } G<B> gb = new G<B>(); G<A> ga = gb; ga. e = new A(); B b = gb. e; // Error! Given B <: A, and assuming G<B> <: G<A>, then: G<A> ga = gb; would be legal. In Java, type is erased.

Bounded Wildcard A wildcard does not allow doing much To provide operations with wildcard types, one can specify bounds: Upper Bound The ancestor of unknown: G<? extends X> Java G<T> where T : X C# Lower Bound The descendant of unknown: G<? super Y> Java G<T> where Y : T C#

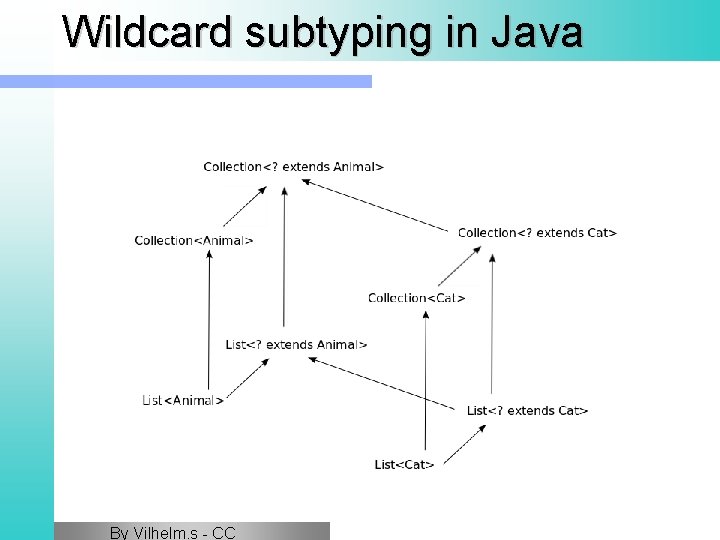
Bounded Wildcards Subtyping Rules For any B such that B <: A: l G<B> <: G<? extends A> l G<A> <: G<? super B>

Bounded Wildcards - Example G<A> ga = new G<A>(); G<B> gb = new G<B>(); G<? extends A> gea = gb; // Can read from A a = gea. e; G<? super B> gsb = ga; // Can write to gsb. e = new B(); G<B> <: G<? extends A> hence legal G<A> <: G<? super B> hence legal

Wildcard subtyping in Java By Vilhelm. s - CC

Generics and Polymorphism class Shape { void draw() {…} } class Circle extends Shape { void draw() {…} } class Rectangle extends Shape { void draw() {…} } public void draw. All(Collection<Shape> shapes) { for (Shape s: shapes) s. draw(); } l l Does not work. Why? Cannot be used on Collection<Circle>

Bounded Polymorphism l Bind the wildcard: replace the type Collection<Shape> with Collection<? extends Shape>: public void draw. All(Collection<? extends Shape> shapes) { for (Shape s: shapes) s. draw(); } Now draw. All() will accept lists of any subclass of Shape l The ? Stands for an unknown subtype of Shape l The type Shape is the upper bound of the wildcard l

Bounded Wildcard l There is a problem when using wildcards: public void add. Circle(Collection<? extends Shape> shapes) { shapes. add(new Circle()); } l What will happen? Why?

Covariance, Contravariance, Invariance Given types A and B such that B <: A, a type constructor G is said: l Covariant: if G<B> <: G<A> l Contravariant: if G<A> <: G<B> l Invariant: if neither covariant nor contravariant

C# Variance Declaration interface IEnumerator<out T> { T Current { get; } bool Move. Next(); The type of a result is covariant } public delegate void Action<in T>(T obj); a function argument is contravariant Action<Shape> b = (shape) => { shape. draw(); }; Action<Circle> d = b; // Action<Shape> <: Action<Circle> d(new Circle()); Action<Object> o = b; // illegal l A covariant type parameter can be used as the return type of a delegate l A contravariant type parameters can be used as parameter types

Substitutability Principle l If S is a subtype of T, then objects of type T may be replaced with objects of type S without altering any of the desirable properties of that program (e. g. correctness).

Liskov Substitution Principle Let (x) be a true property of objects x of type T. Then (y) should be true for objects y of type S where S is a subtype of T. l Behavioral subtyping is a stronger notion than nominal or structural subtyping

Nominal Subtyping (Duck Typing) l If objects of class A can handle all of the messages that objects of class B can handle (that is, if they define all the same methods), then A is a subtype of B regardless of inheritance. If it walks like a duck and swims like a duck and quacks like a duck, I call it a duck.

Structural Subtyping In structural typing, an element is considered to be compatible with another if, for each feature within the second element's type, there is a corresponding and identical feature in the first element's type. l Subtype polymorphism is structural subtyping l Inheritance is not subtyping in structurallytyped OO languages: l § if a class defines a methods that takes arguments or returns values of its own type

Liskov Signature Requirements Matching function or method types involves deciding on subtyping on method signatures l Methods argument types must obey contravariance l Return types must obey covariance l

Examples l Assuming § Cat <: Animal § Enumerable<T> is covariant on T § Action<T> is contravariant on T Enumerable<Cat> is a subtype of Enumerable<Animal>. The subtyping is preserved. l Action<Animal> is a subtype of Action<Cat>. The subtyping is reversed. l Neither List<Cat> nor List<Animal> is a subtype of the other, because List<T> is invariant on T. l

A Typical Violation l Class Square derived from class Rectangle, if for example methods from class Rectangle are allowed to change width/height independently

Contravariance of Arguments Types public class Super. Type { public virtual string Age. String(short age) { return age. To. String(); } } public class LSPLegal. Sub. Type : Super. Type { public override string Age. String(int age) { // This is legal due to the Contravariance requirement // widening the argument type is allowed return age. To. String(); } } public class LSPIllegal. Sub. Type : Super. Type { public override string Age. String(byte age) { // illegal due to the Contravariance requirement return base. Age. String((short)age); } }

Covariance of return Type public class Super. Type { public virtual int Days. Since. Last. Login(User user) { return int. Max. Value; } } public class LSPLegal. Sub. Type : Super. Type { public override short Days. Since. Last. Login(User user) { return short. Max. Value; // Legal because it will always fit into a n int } } public class LSPIllegal. Sub. Type : Super. Type { public override long Days. Since. Last. Login(User user) { return long. Max. Value; // Illegal because it will not surely fit into an int } }

To wildcard or not to wildcard? l That is the question: interface Collection<E> { public boolean contains. All(Collection<? > c); public boolean add. All(Collection<? extends E> c); } interface Collection<E> { public <T> boolean contains. All(Collection<T> c); public <T extends E> boolean add. All(Collection<T> c); }

Lower Bound Example interface sink<T> { flush(T t); } public <T> T flush. All(Collection<T> col, Sink<T> sink) { T last; for (T t: col) { last = t; sink. flush(t); } return last; }

Lower Bound Example (2) Sink<Object> s; Collection<String> cs; String str = flush. All(cs, s); // Error!

Lower Bound Example (3) public <T> T flush. All(Collection<T> col, Sink<T> sink) { …} … String str = flush. All(cs, s); // Error! T is now solvable as Object, but it is not the correct type: it should be String

Lower Bound Example (4) public <T> T flush. All(Collection<T> col, Sink<? Super T> sink) { … } … String str = flush. All(cs, s); // OK!

Combining generics and inheritance l The inheritance relation must be extended with a new subtyping rule: Given class C<T 1, . . . , Tn> extends B we have C<t 1, . . . , tn> <: B[t 1/T 1, . . . , tn/Tn] Can now cast up and down to Object safely l Note: types must be substituted because the super-class can be parametric l

Manipulating types l l Grouping values into types has helped us to build better compilers Could we do the same with types? Types can be grouped by means of inheritance which represents the union of type sets Parametric types combined with inheritance allow expressing function on types: class Stack<T: Object> : Container Function name Function arguments Result type

Example: generic containers class Row<T : Control> : Control { /* row of graphic controls *> } class Column<T : Control> : Control { /* column of graphic controls */ } class Table<T : Control> : Row<Column<T>> { /* Table of graphic controls */ } … // It generates the keypad of a calculator Table<Button> t = new Table<Button>(3, 3); for (int i = 0; i < 3; i++) for (int j = 0; j < 3; j++) t[i, j]. Text = (i * 3 + j + 1). To. String();