Parametric functions areas KUS objectives BAT Find the

Parametric functions: areas KUS objectives BAT Find the area under a curve when it is given in parametric equations Find the point on the curve y = f(x) when t = -1 Find the Cartesian equation y = f(x) from the parametric equations Find the Area under the curve y = f(x) between t = 1 and t = 2

Notes areas under curves When a curve is given in parametric equations we can use the following

Work out dx/dt Then substitute in y and Use calculator to check dx/ dt

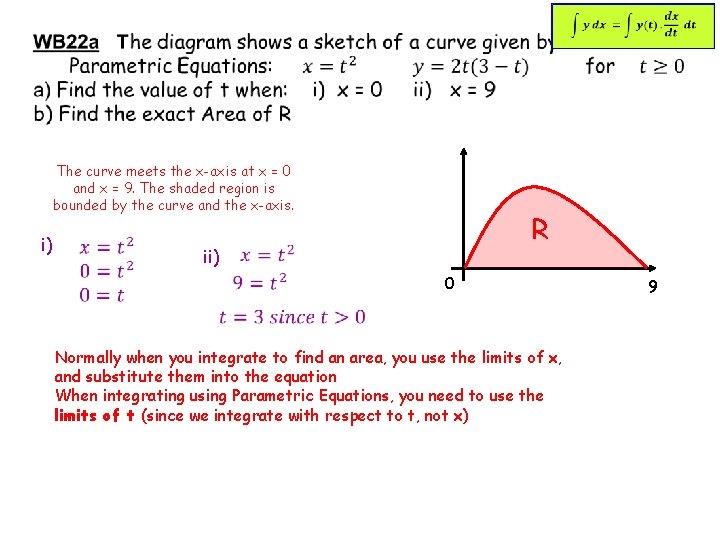
The curve meets the x-axis at x = 0 and x = 9. The shaded region is bounded by the curve and the x-axis. i) R ii) 0 Normally when you integrate to find an area, you use the limits of x, and substitute them into the equation When integrating using Parametric Equations, you need to use the limits of t (since we integrate with respect to t, not x) 9

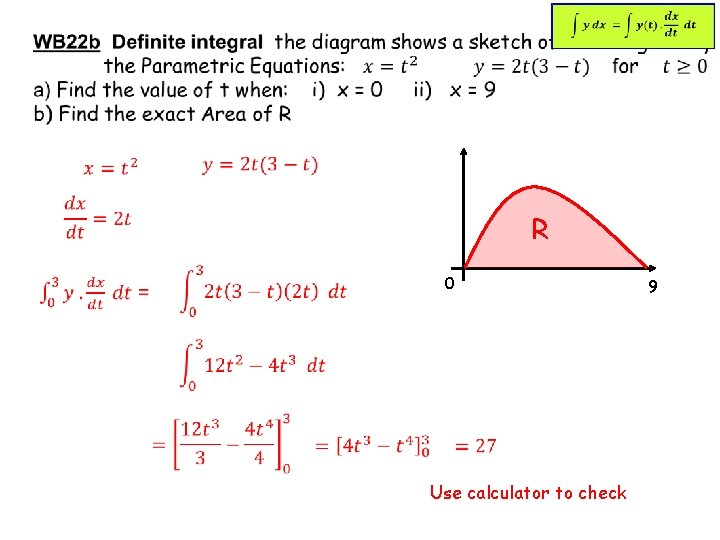
R 0 Use calculator to check 9

We have the x limits, we need the t limits 0 8 Our t values are 0 and ± 2 We have 3 t values. We now have to integrate twice, once using 2 and once using -2 One gives the area above the x-axis, and the other the area below (in this case the areas are equal since the graph is symmetrical) At this point we could just double the answer (as the graph is symmetrical), but to show you the other pair gives the same answer keep going

0 Same area as before so Double gives Total area 8

Use calculator to check

The boundaries/limits for have been given in the Question Use Trig identity Use calculator to check

You should be able to: KUS objectives BAT Find the area under a curve when it is given in parametric equations Write one thing you have learned Write one thing you need to improve

END