Parameter Redundancy and Identifiability in Ecological Models Diana

Parameter Redundancy and Identifiability in Ecological Models Diana Cole, University of Kent
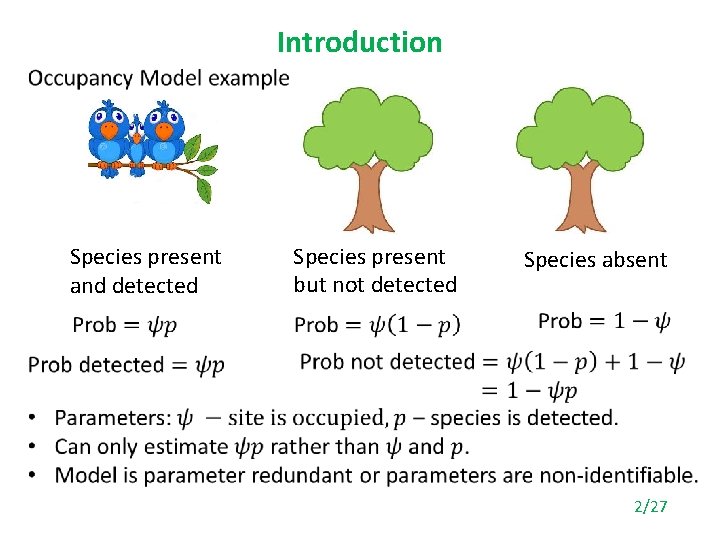
Introduction • x Species present and detected Species present but not detected Species absent 2/27

Parameter Redundancy and Identifiability • 3/27

Problems with Parameter Redundancy • There will be a flat ridge in the likelihood of a parameter redundant model (Catchpole and Morgan, 1997), resulting in more than one set of maximum likelihood estimates. • Numerical methods to find the MLE will not pick up the flat ridge, although it could be picked up by trying multiple starting values and looking at profile log-likelihoods. • The Fisher information matrix will be singular (Rothenberg, 1971) and therefore the standard errors will be undefined. • However the exact Fisher information matrix is rarely known. Standard errors are typically approximated using a Hessian matrix obtained numerically. Can parameter redundancy be detected from the standard errors? 4/27

Is example 1 parameter redundant? Parameter Estimate 0. 39 0. 64 0. 09 0. 18 Standard Error imaginary 0. 061 imaginary 5/27

Is example 2 parameter redundant? Parameter Estimate 0. 41 0. 83 0. 10 0. 19 Standard Error 0. 70 0. 07 0. 11 0. 33 6/27

Is example 3 parameter redundant? Parameter Estimate 0. 37 0. 48 0. 39 0. 34 0. 40 0. 65 0. 10 0. 18 Standard Error 0. 19 0. 20 0. 17 0. 20 0. 06 0. 03 0. 09 • 7/27
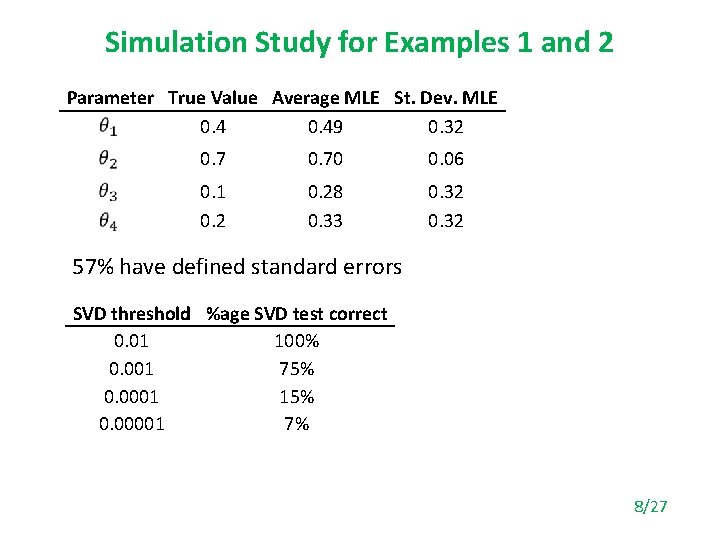
Simulation Study for Examples 1 and 2 Parameter True Value Average MLE St. Dev. MLE 0. 49 0. 32 0. 70 0. 06 0. 1 0. 28 0. 33 0. 32 57% have defined standard errors SVD threshold %age SVD test correct 0. 01 100% 0. 001 75% 0. 0001 15% 0. 00001 7% 8/27

Mark-Recovery Models • ¬ 63 ¬ 64 ¬ 65 Ringing yr 63 64 65 Recapture yr 63 64 65 9/27
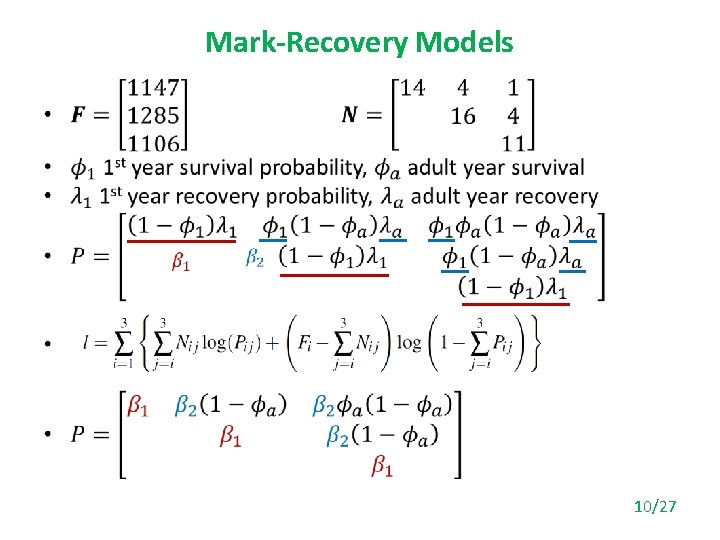
Mark-Recovery Models • 10/27

Symbolic Method (Cole et al, 2010 and Cole et al, 2012) • Exhaustive summary – unique representation of the model • Parameters 11/27

Symbolic Method • 12/27

Estimable Parameter Combinations • 13/27

Other uses of symbolic method • Uses of symbolic method: – Catchpole and Morgan (1997) exponential family models, mostly used in ecological statistics, – Rothenberg (1971) original general use, econometric examples, – Goodman (1974) latent class models, – Sharpio (1986) non-linear regression models, – Pohjanpalo (1982) first use for compartment models, – Cole et al (2010) General exhaustive summary framework, – Cole et al (2012) Mark-recovery models. • Finding estimable parameters: – Catchpole et al (1998) exponential family models, – Chappell and Gunn (1998) and Evans and Chappell (2000) compartment models, – Cole et al (2010) General exhaustive summary framework.

Problem with Symbolic Method • The key to the symbolic method for detecting parameter redundancy is to find a derivative matrix and its rank. • Models are getting more complex. • The derivative matrix is therefore structurally more complex. • Maple runs out of memory calculating the rank. Wandering Albatross Multi-state models for sea birds Hunter and Caswell (2009) Cole (2012) Striped Sea Bass Tag-return models for fish Jiang et al (2007) Cole and Morgan (2010) • How do you proceed? – Numerically – but only valid for specific value of parameters. But can’t find combinations of parameters you can estimate. Not possible to generalise results. – Symbolically – involves extending theory, again it involves a derivative matrix and its rank, but the derivative matrix is structurally simpler. – Hybrid-Symbolic Numeric Method. 15/27
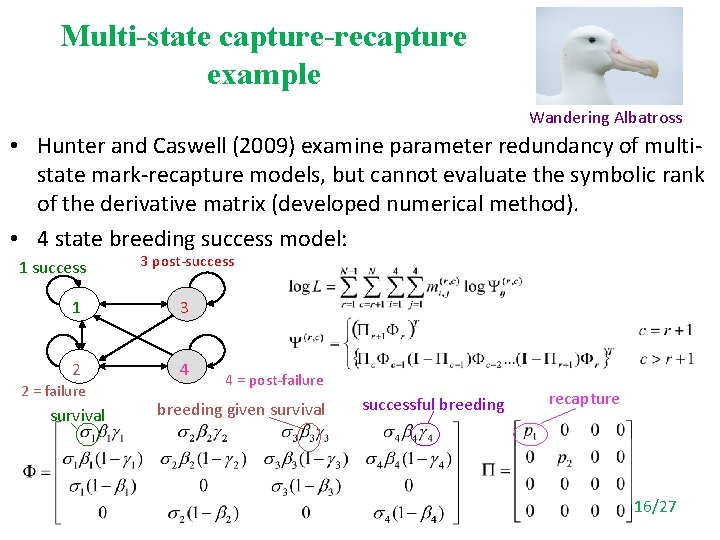
Multi-state capture-recapture example Wandering Albatross • Hunter and Caswell (2009) examine parameter redundancy of multistate mark-recapture models, but cannot evaluate the symbolic rank of the derivative matrix (developed numerical method). • 4 state breeding success model: 1 success 3 post-success 1 3 2 4 2 = failure survival 4 = post-failure breeding given survival successful breeding recapture 16/27

Extended Symbolic Method Cole et al (2010) 1. Choose a reparameterisation, s, that simplifies the model structure. 2. Rewrite the exhaustive summary, ( ), in terms of the reparameterisation - (s). 17/27

Extended Symbolic Method 3. Calculate the derivative matrix Ds. 4. The no. of estimable parameters =rank(Ds) = 12, no. est. pars = 12, deficiency = 14 – 12 = 2 5. If Ds is full rank s = sre is a reduced-form exhaustive summary. If Ds is not full rank solve set of PDE to find a reduced-form exhaustive summary, sre.

Extended Symbolic Method 6. Use sre as an exhaustive summary. Survival Constraint Breeding Constraint 1 = 2 = 3 = 4 1 = 3 , 2 = 4 1 = 2 , 3 = 4 1 , 2 , 3, 4 1= 2= 3= 4 0 (8) 0 (9) 1 (11) 1= 3 , 2= 4 0 (9) 0 (10) 2 (12) 1= 2, 3= 4 0 (9) 0 (10) 1 (12) 1, 2, 3, 4 0 (11) 0 (12) 2 (14)
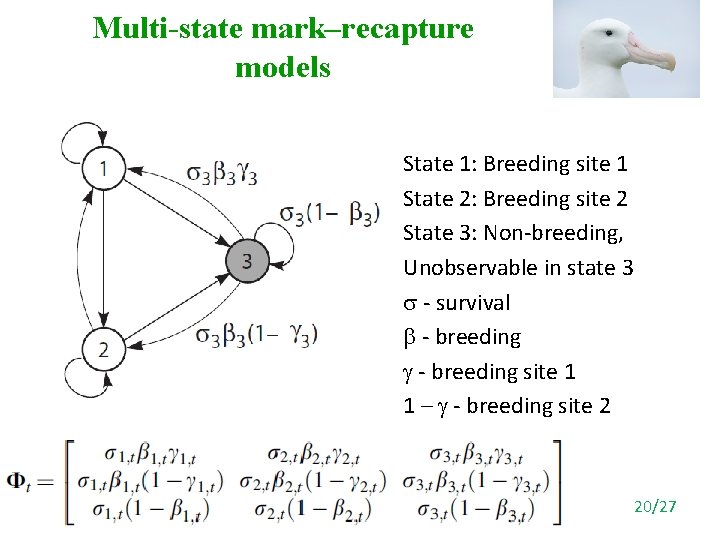
Multi-state mark–recapture models State 1: Breeding site 1 State 2: Breeding site 2 State 3: Non-breeding, Unobservable in state 3 - survival - breeding site 1 1 – - breeding site 2 20/27

Multi-state mark–recapture models – General Model • General Multistate-model has S states, with the last U states unobservable with N years of data. • Survival probabilities released in year r captured in year c: • t is an S S matrix of transition probabilities at time t with transition probabilities i, j(t) = ai, j(t). • Pt is an S S diagonal matrix of probabilities of capture pt. • pt = 0 for an unobservable state, 21/27

General simpler exhaustive summary Cole (2012) r = 10 N – 17 d=N+3 22/27

Hybrid Symbolic-Numeric Method Choquet and Cole (2012) • 23/27

Example – multi-site capture-recapture model • 24/27
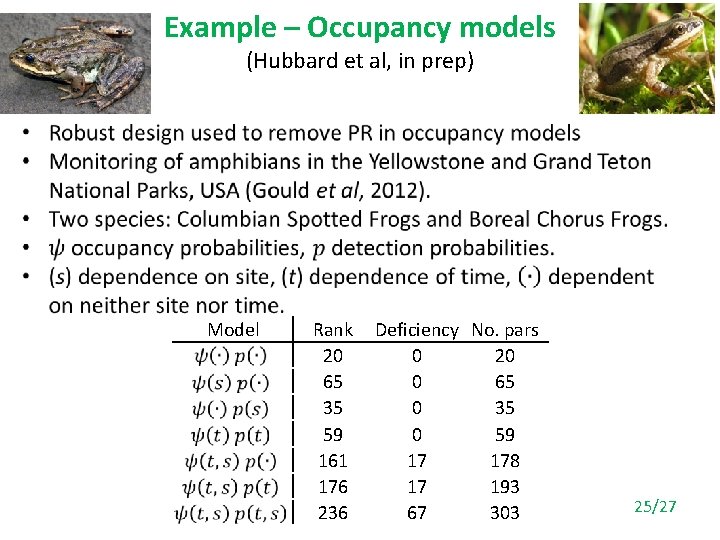
Example – Occupancy models (Hubbard et al, in prep) • Model Rank 20 65 35 59 161 176 236 Deficiency No. pars 0 20 0 65 0 35 0 59 17 178 17 193 67 303 25/27
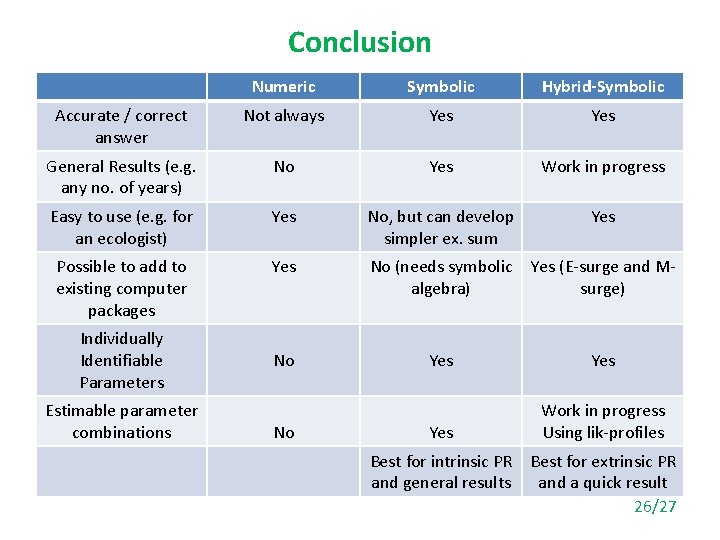
Conclusion Numeric Symbolic Hybrid-Symbolic Accurate / correct answer Not always Yes General Results (e. g. any no. of years) No Yes Work in progress Easy to use (e. g. for an ecologist) Yes No, but can develop simpler ex. sum Yes Possible to add to existing computer packages Yes No (needs symbolic Yes (E-surge and Malgebra) surge) Individually Identifiable Parameters Estimable parameter combinations No No Yes Yes Work in progress Using lik-profiles Best for intrinsic PR Best for extrinsic PR and general results and a quick result 26/27

References http: //www. kent. ac. uk/smsas/personal/djc 24/parameterredundancy. htm – – – – – Brownie, C. Hines, J. , Nichols, J. et al (1993) Biometrics, 49, p 1173. Catchpole, E. A. and Morgan, B. J. T. (1997) Biometrika, 84, 187 -196 Catchpole, E. A. , Morgan, B. J. T. and Freeman, S. N. (1998) Biometrika, 85, 462 -468 Chappell, M. J. and Gunn, R. N. (1998) Mathematical Biosciences, 148, 21 -41. Choquet, R. and Cole, D. J. (2012) Mathematical Biosciences, 236, p 117. Cole, D. J. and Morgan, B. J. T. (2010) JABES, 15, 431 -434. Cole, D. J. , Morgan, B. J. T and Titterington, D. M. (2010) Mathematical Biosciences, 228, 16– 30. Cole, D. J. (2012) Journal of Ornithology, 152, S 305 -S 315. Cole, D. J. , Morgan, B. J. T. , Catchpole, E. A. and Hubbard, B. A. (2012) Biometrical Journal, 54, 507 -523. Cole, D. J. , Morgan, B. J. T. , Mc. Crea, R. S, Pradel, R. , Gimenez, O. and Choquet, R. (2014) Ecology and Evolution, 4, 2124 -2133, Evans, N. D. and Chappell, M. J. (2000) Mathematical Biosciences, 168, 137 -159. Gould, W. R. , Patla, D. A. , Daley, R. , et al (2012). Wetlands, 32, p 379. Goodman, L. A. (1974) Biometrika, 61, 215 -231. Hunter, C. M. and Caswell, H. (2009). Ecological and Environmental Statistics, 3, 797 -825 Jiang, H. Pollock, K. H. , Brownie, C. , et al (2007) JABES, 12, 177 -194 Pohjanpalo, H. (1982) Technical Research Centre of Finland Research Report No. 56. Rothenberg, T. J. (1971) Econometrica, 39, 577 -591. Shapiro, A. (1986) Journal of the American Statistical Association, 81, 142 -149. Viallefont, A. , Lebreton, J. D. , Reboulet, A. M. and Gory, G. (1998) Biometrical Journal, 40, 313 -325. 27/27
- Slides: 27