Parameter Estimation Covered only ML estimator n Given

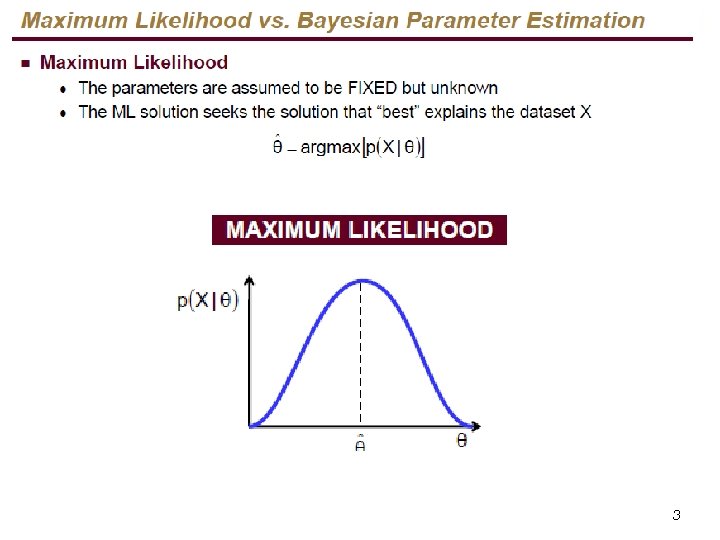
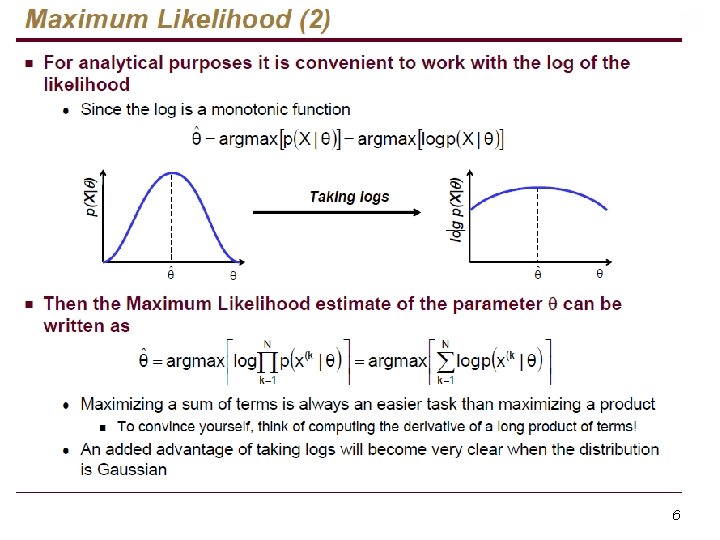
Parameter Estimation Covered only ML estimator

n Given an i. i. d data set X, sampled from a distribution with parameters q, we would like to determine these parameters, given the samples. n Once we have those, we can estimate p(x) for any given x, given the known distribution. n Two approaches in parameter estimation: Maximum Likelihood approach ¨ Bayesian approach (will not be covered in this course) ¨ 2

3

4

5

6

ML estimates for Binomial and Multinomial distributions

Examples: Bernoulli/Multinomial n Bernouilli: Binary random variable x may take one of the two values: ¨ success/failure, 0/1 with probabilities: P(x=1)= po ¨ P(x=0)=1 -po ¨ ¨ Unifying the above, we get: P (x) = pox (1 – po ) (1 – x) n n Note that the single formula helps rather than having two separate formulas (one for x=1 and one for x=0) Given a sample set X={x 1, x 2, …}, we can estimate p 0 using the ML estimate by maximizing the log-likelihood of the sample set: t t Log likelihood (po) : log P(X|po) = log ∏t pox (1 – po ) (1 – x ) 8

Examples: Bernoulli log L=log P(X|po) = log ∏t poxt (1 – po ) (1 – xt) t=1, N and xt in {0, 1} = St log ( poxt (1 – po ) (1 – xt) ) St log poxt + log (1 – po ) (1 – xt) = St ( xt log po + (1 – xt) log (1 – po ) ) = In solving for the necessary condition for extrema, we must have dlog. L/dpo = 0. Take derivative, set to 0 and solve. . . : dlog. L/dpo = St xt. (1/po) + St (1 – xt). 1/ (1 – po ). -1 = 0 Remember: derivative of log x is 1/x. St x. (1/po) St (1 – xt). 1/ (1 – po ) => St xt. (1 – po ) = St (1 – xt). po t t S x - po S x = S po – po S xt t t = => St xt = St po = Npo => MLE: po = ∑t xt /N 9

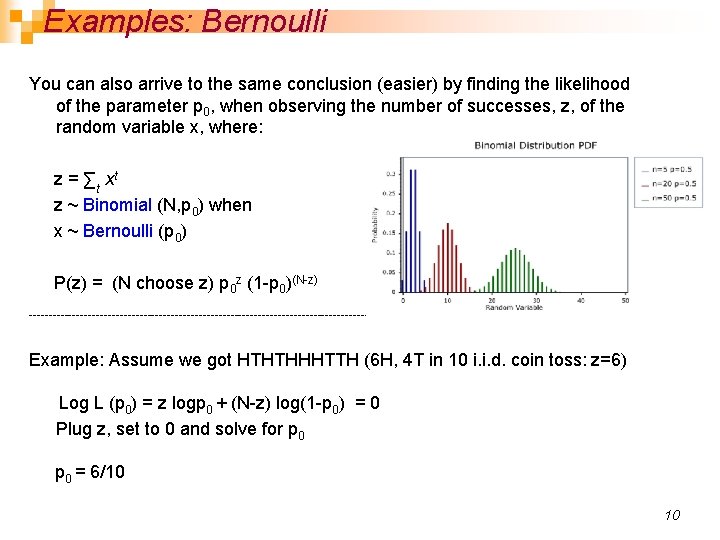
Examples: Bernoulli You can also arrive to the same conclusion (easier) by finding the likelihood of the parameter p 0, when observing the number of successes, z, of the random variable x, where: z = ∑t xt z ~ Binomial (N, p 0) when x ~ Bernoulli (p 0) P(z) = (N choose z) p 0 z (1 -p 0)(N-z) -------------------------------------------------- Example: Assume we got HTHTHHHTTH (6 H, 4 T in 10 i. i. d. coin toss: z=6) Log L (p 0) = z logp 0 + (N-z) log(1 -p 0) = 0 Plug z, set to 0 and solve for p 0 = 6/10 10

Examples: Categorical Bernoulli -> Binomial Categorical –> Multinomial n Categorical: K>2 states, xi in {0, 1} n Instead of two states, we now have K mutually exclusive and exhaustive events, with probability of occurence of pi where Sipi = 1. Ex. A dice with 6 possible outcomes. n P(x=1)= p 1 ¨ P(x=2)= p 2. . P(x=6)= p 6 ¨ ¨ x = [1 0 0 0] = [x 1. . . x 6] Unifying the above, we get: P (x) = ∏i pixi where xi is 1 if outcome is state i 0 otherwise Similar to p(x) = px(1 -p)(1 -x) when there were two possible outcomes for x log L(p 1, p 2, . . . , p. K|X) = log ∏t ∏i pixit MLE: pi = ∑t xit / N Ratio of experiments with outcome of state i (e. g. 60 dice throws, 15 of them were 6 p 6 = 15/60 11

ML estimates for 1 D-Gaussian distributions

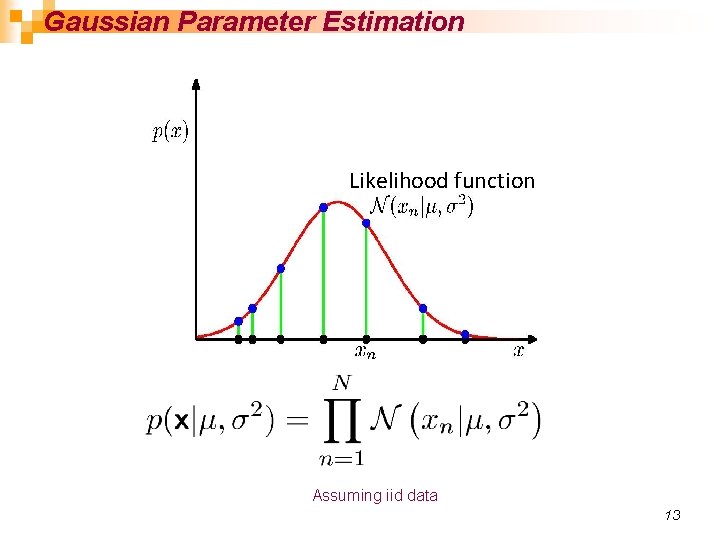
Gaussian Parameter Estimation Likelihood function Assuming iid data 13

14

Reminder n In order to maximize or minimize a function f(x) w. r. to x, ¨ we compute the derivative df(x)/dx and set to 0, since a necessary condition for extrema is that the derivative is 0. n Commonly used derivative rules are given on the right. 15

Derivation – general case 16

Maximum (Log) Likelihood for a 1 D-Gaussian In other words, maximum likelihood estimates of mean and variance are the same as sample mean and variance. 17