Parallelizing Legacy Applications in Message Passing Programming Model

Parallelizing Legacy Applications in Message Passing Programming Model and the Example of MOPAC Tseng-Hui (Frank) Lin thlin@npac. syr. edu tsenglin@us. ibm. com April 7, 2000

Legacy Applications • Performed functions still useful • Large user population • Invested big money • Rewriting is expensive • Rewriting is risky • Changed through long time period • Modified by diff people • Historical code • Dead code • Old concepts • Major bugs fixed April 7, 2000 2

What Legacy Applications Need • Provide higher resolution • Run bigger data • Graphic representation for scientific data • Keep certified April 7, 2000 3

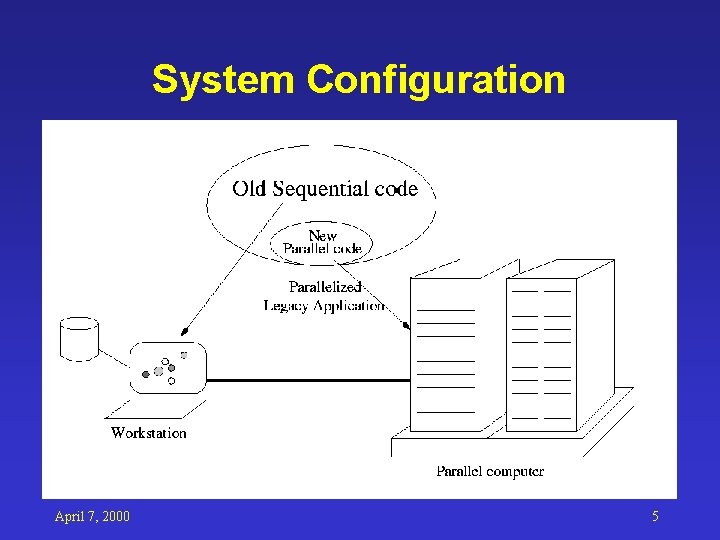
How to Meet the Requirements Ö Improve performance: Parallel computing Ö Keep Certified: Change critical parts only • Better user interface: Add GUI April 7, 2000 4

System Configuration April 7, 2000 5

Distributed vs Shared Memory April 7, 2000 6

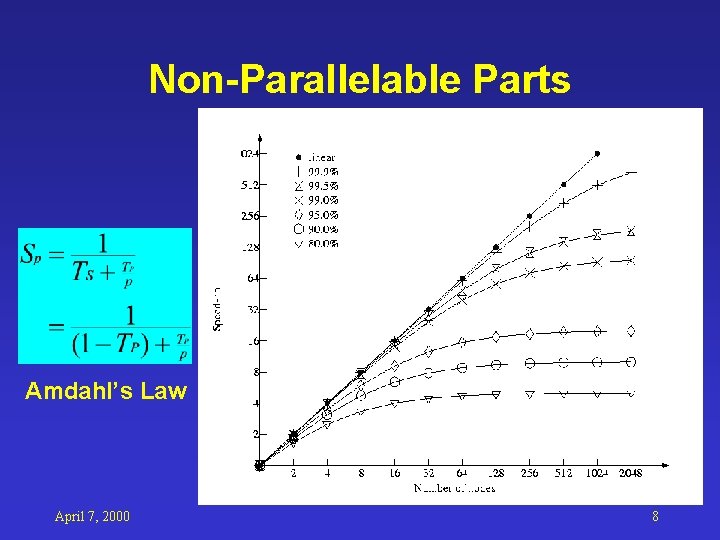
Message Passing Programming • Non-parallelizable parts – Data dependent forces sequential execution – Not worthy to parallelize • Workload distribution • Input data distribution • Distributed Computation – Load balance • Results collection April 7, 2000 7

Non-Parallelable Parts Amdahl’s Law April 7, 2000 8

MOPAC • Semi-empirical molecular orbital pkg – MNDO, MINDO/3, AM 1, PM 3 • MOPAC 3 submitted to QCPE in 1985 • MOPAC 6 ported to many platforms – VMS – UNIX (our work based on this version) – DOS/Windows • MOPAC 7 is current April 7, 2000 9

MOPAC input file Keywords L 1 : L 2 : L 3 : L 41: L 42: L 43: L 44: L 45: L 46: L 5 : UHF PULAY MINDO 3 VECTORS DENSITY LOCAL T=300 Title EXAMPLE OF DATA FOR MOPAC MINDO/3 UHF CLOSED-SHELL D 2 D ETHYLENE C Comments C 1. 400118 1 H 1. 098326 1 123. 572063 1 180. 000000 0 2 1 3 H 1. 098326 1 123. 572063 1 90. 000000 0 1 2 3 H 1. 098326 1 123. 572063 1 270. 000000 0 1 2 3 April 7, 2000 Blank Line End-of-Data Molecule Structure in Z-matrix (Internal Coordinate) 10

Hartree-Fock Self Consistent Field Schrödinger equation Matrix equation form (3. 1. 3) Matrix representation of Fock matrix (3. 1. 4) April 7, 2000 11

HF-SCF Procedure S 1: Calc molecular integrals O(n 4) S 2: Guess initial eigenvector C S 3: Use C to compute F O(n 4) S 4: Transform F to orthogonal basis O(n 3) diagonalize F to get a new C O(n 3) S 5: Stop if C converged S 6: Guess new C and goto S 3 April 7, 2000 12

MOPAC computation • Ab initio HF-SCF – evaluate all integrals rigorously – accuracy – requires high computing power – limited molecule size • Semi-empirical HF-SCF – use the same procedure – reduce computational complexity – support larger molecule size April 7, 2000 13

Semi-empirical SCF • Ignore some integrals • Use experiment results to replace integrals • Assume AO basis is orthogonal S 1, S 3: O(n 4)=>O(n 2) S 4 orthogonalization not needed New bottle neck: diagonalization Complexity: O(n 3) April 7, 2000 14

Parallelization Procedure • Sequential analysis – Time profiling analysis – Program flow analysis – Complexity analysis • Parallel analysis – Data dependence resolution – Loop parallelization • Integration – Communication between modules April 7, 2000 15

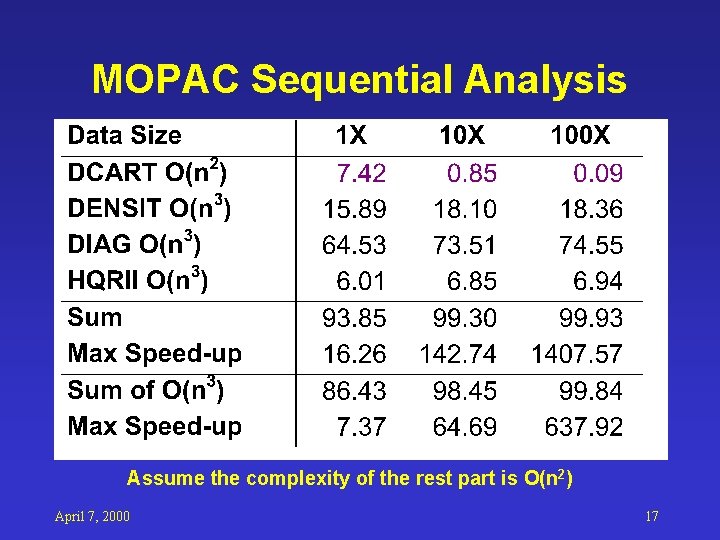
Sequential Analysis • Time profiling analysis – Pick up the computational intensive parts – Usually use smaller input data • Program flow analysis – Verify the chosen ones are commonly used – Domain expert not required • Complexity analysis – Workload distribution changed significantly for different data sizes April 7, 2000 16

MOPAC Sequential Analysis Assume the complexity of the rest part is O(n 2) April 7, 2000 17

Loop Parallelization • Scalar forward subst: remove temp vars • Induction variable subst: resolv depend • Loop interchange/merge enlarge granularity, reduce synchronization • Scalar expansion resolve data dependence on scalars • Variable copying resolve data dependence on arrays April 7, 2000 18

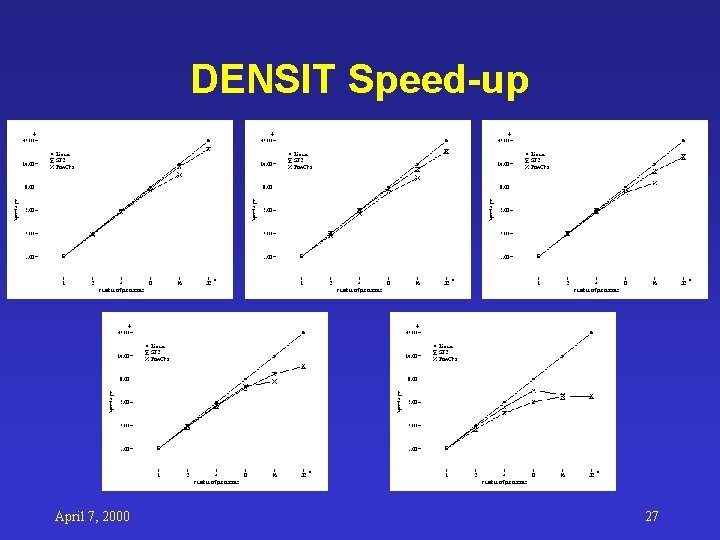
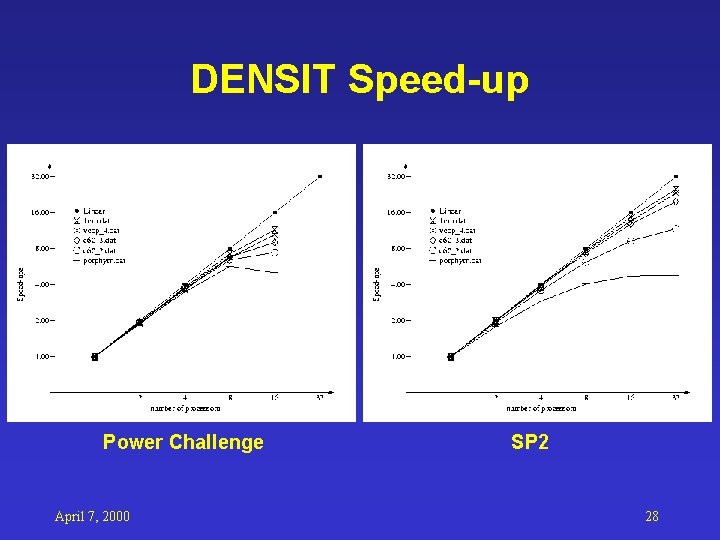
MOPAC Parallelization: DENSIT • • Function: compute density matrix 2 1 -level loops inside of a 2 -level loop Triangular computational space Merge the outer 2 -level loop to 1 loop with range [1. . n(n+1)/2] • Lower comp/comm ratio (when n small) • benefit from low latency communication when n is small April 7, 2000 19

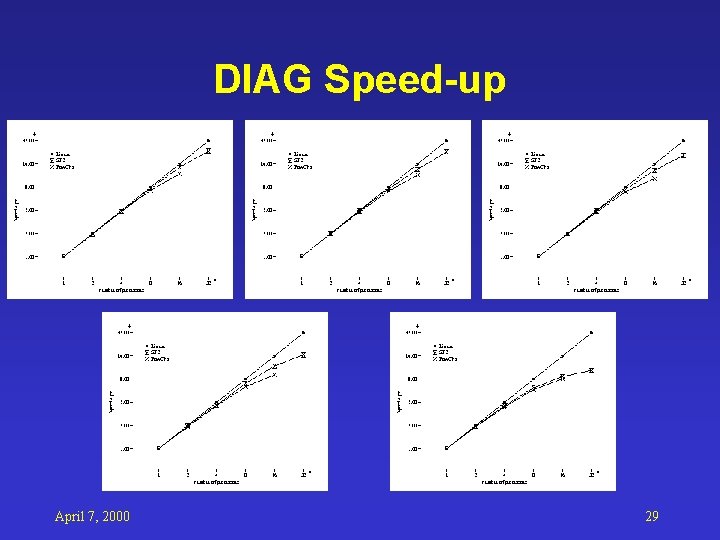
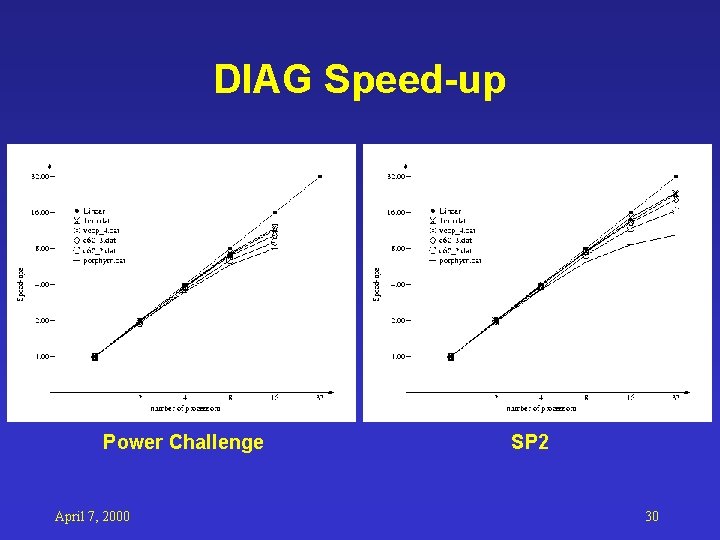
MOPAC Parallelization: DIAG • P 1: Generate Fock modular orbital matrix – Higher comp/comm ratio – Find global maximum TINY from local ones – Need to re-distribute matrix FMO for Part 2 • P 2: 2 X 2 rotation to eliminate significant off-diagonal elements – “if” structure cause load imbalance – Need to exchange the inner most loop out – Some calculations run on all nodes to save comm April 7, 2000 20

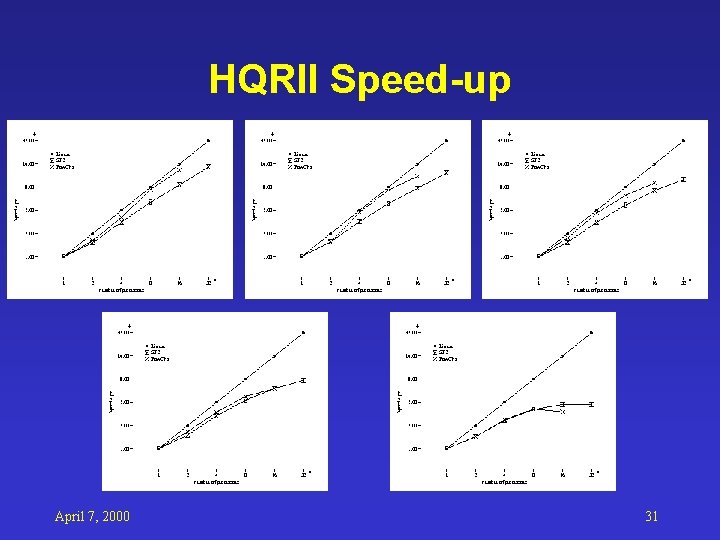
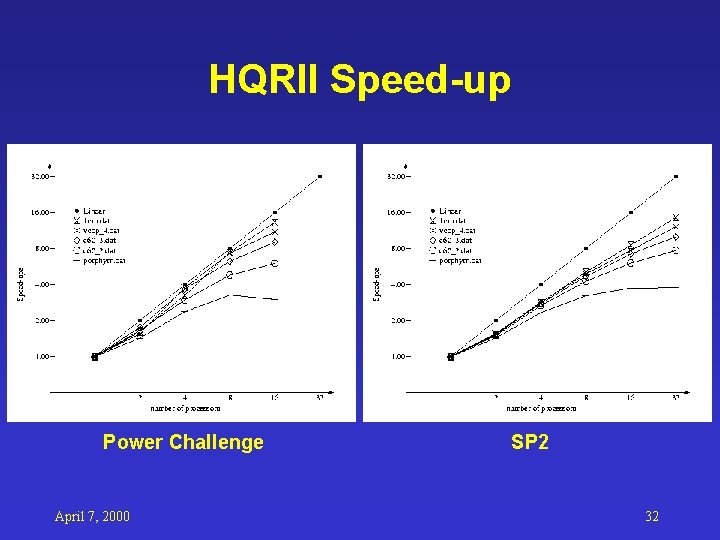
MOPAC Parallelization: HQRII • • • Function: standard eigensolver R. J. Allen survey Use PNNL Pe. IGS pdspevx() function Use MPI communication library Small chunk data exchange, good if n/p>8 Implemented in C, different way to pack matrix (row major) April 7, 2000 21

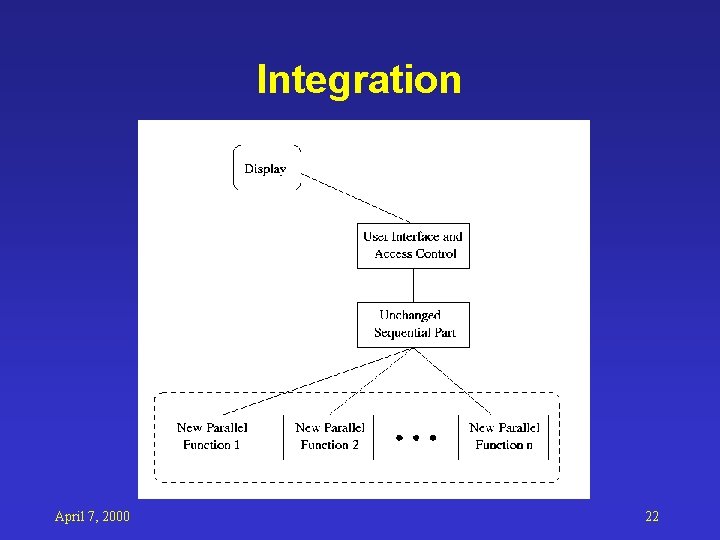
Integration April 7, 2000 22

Comm between Modules • Parallel - sequential – Use TCP/IP – Auto upgrade to shared memory if possible • Sequential - user interface – Input and output files – Application/Advanced Visualization System (AVS) remote module communication • User interface - display – AVS April 7, 2000 23

MOPAC Cntl Panel & Module April 7, 2000 24

MOPAC GUI April 7, 2000 25

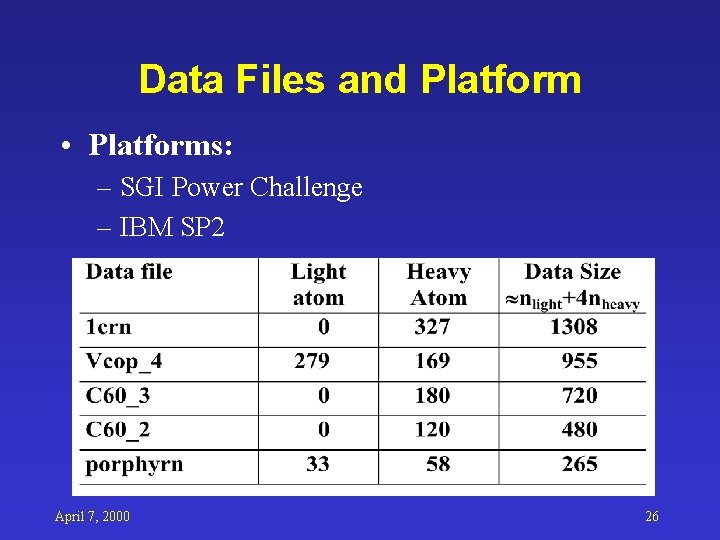
Data Files and Platform • Platforms: – SGI Power Challenge – IBM SP 2 April 7, 2000 26

DENSIT Speed-up April 7, 2000 27

DENSIT Speed-up Power Challenge April 7, 2000 SP 2 28

DIAG Speed-up April 7, 2000 29

DIAG Speed-up Power Challenge April 7, 2000 SP 2 30

HQRII Speed-up April 7, 2000 31

HQRII Speed-up Power Challenge April 7, 2000 SP 2 32

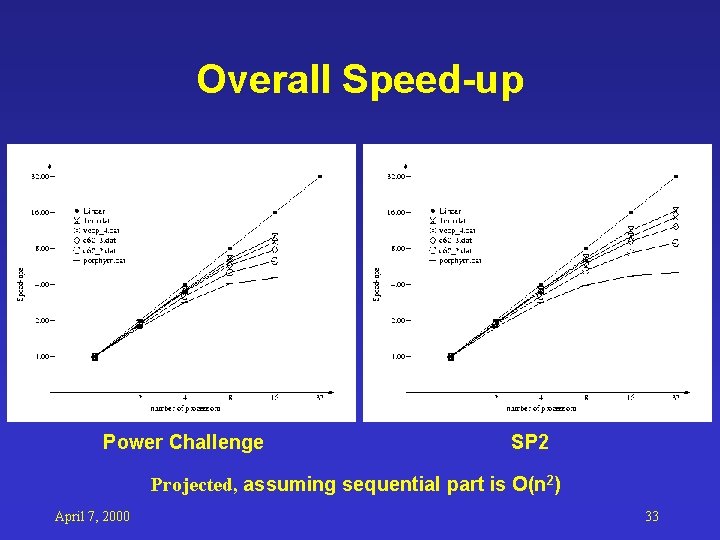
Overall Speed-up Power Challenge SP 2 Projected, assuming sequential part is O(n 2) April 7, 2000 33

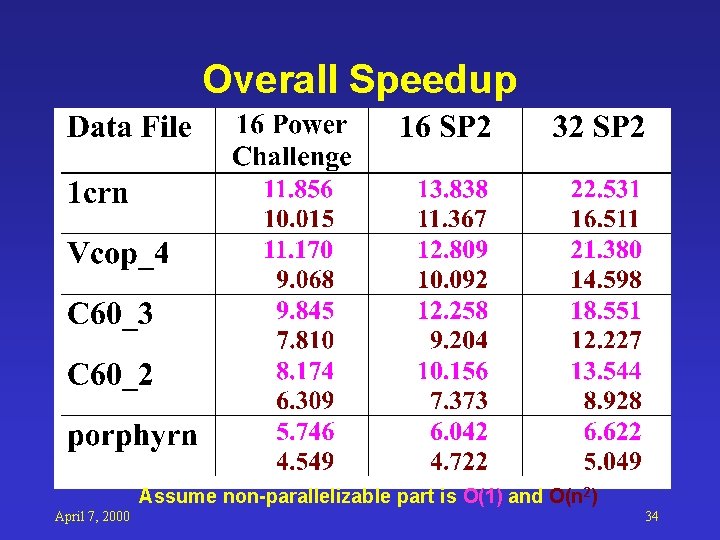
Overall Speedup Assume non-parallelizable part is O(1) and O(n 2) April 7, 2000 34

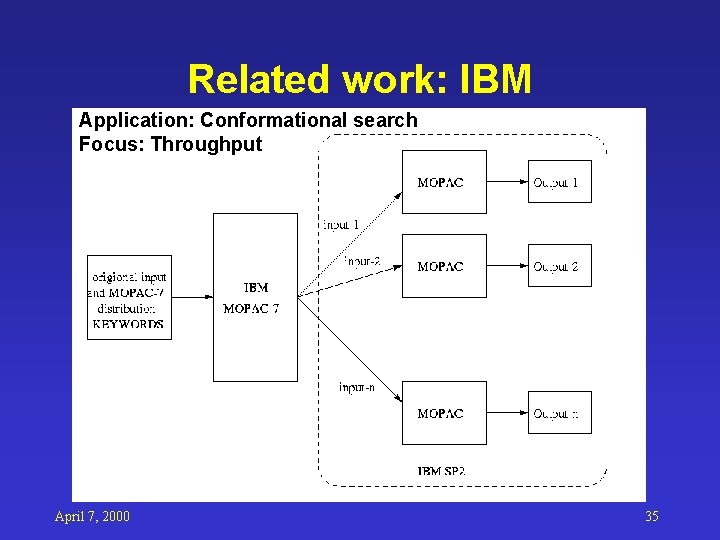
Related work: IBM Application: Conformational search Focus: Throughput April 7, 2000 35

Related work: SDSC • Focus: performance • Parallelizing: – Evaluate electronic repulsion integrals – Calculate first and second derivatives – Solve eigensystem • Platform: 64 -node i. PSC/860 • Results: – Geometry optimization: speedup=5. 2 – Vibration analysis: speedup=40. 8 April 7, 2000 36

Achievements • • Parallelize legacy apps from CS perspective Keep code validated Performance analysis procedures Predict large data performance Optimize parallel code Improve performance Improve user interface April 7, 2000 37

Future Work • • Shared memory model Web based user interface Dynamic node allocation Parallelization of subroutines with lower computational complexity April 7, 2000 38