Parallel Sparse Operations in Matlab Exploring Large Graphs

Parallel Sparse Operations in Matlab: Exploring Large Graphs John R. Gilbert University of California at Santa Barbara Aydin Buluc (UCSB) Brad Mc. Rae (NCEAS) Steve Reinhardt (Interactive Supercomputing) Viral Shah (ISC & UCSB) with thanks to Alan Edelman (MIT & ISC) and Jeremy Kepner (MIT-LL) 1 Support: DOE, NSF, DARPA, SGI, ISC

3 D Spectral Coordinates 2

2 D Histogram: RMAT Graph 3

Strongly Connected Components 4

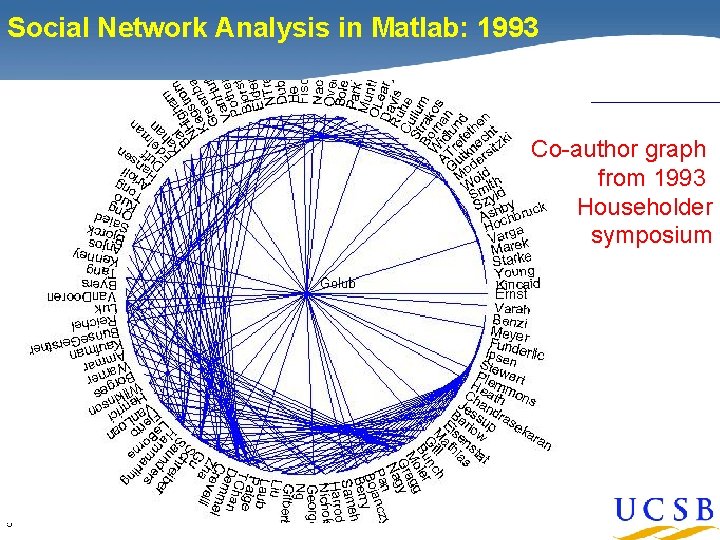
Social Network Analysis in Matlab: 1993 Co-author graph from 1993 Householder symposium 5

Combinatorial Scientific Computing Emerging large scale, high-performance applications: • Web search and information retrieval • Knowledge discovery • Computational biology • Dynamical systems • Machine learning • Bioinformatics • Sparse matrix methods • Geometric modeling • . . . How will combinatorial methods be used by nonexperts? 6

Outline 7 • Infrastructure: Array-based sparse graph computation • An application: Computational ecology • Some nuts and bolts: Sparse matrix multiplication

Matlab*P A = rand(4000*p, 4000*p); x = randn(4000*p, 1); y = zeros(size(x)); while norm(x-y) / norm(x) > 1 e-11 y = x; x = A*x; x = x / norm(x); end; 8

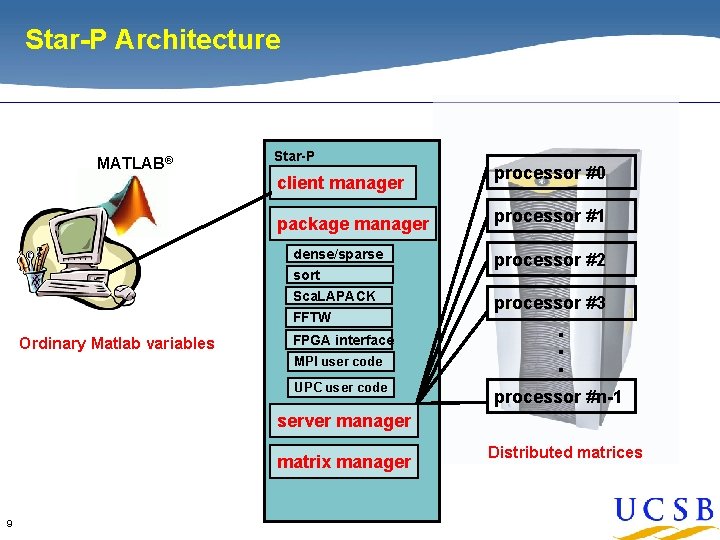
Star-P Architecture Star-P client manager package manager processor #1 dense/sparse sort processor #2 Sca. LAPACK processor #3 FFTW Ordinary Matlab variables processor #0 FPGA interface MPI user code UPC user code . . . MATLAB® processor #n-1 server manager matrix manager 9 Distributed matrices

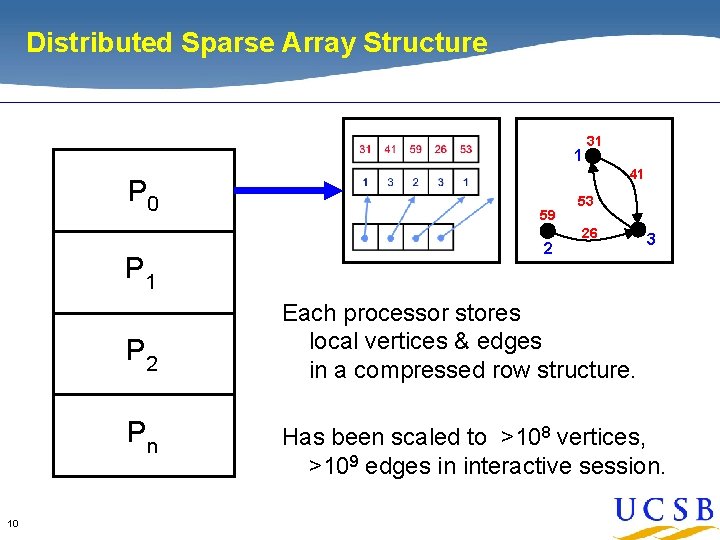
Distributed Sparse Array Structure 1 P 0 P 1 P 2 Pn 10 31 41 59 2 53 26 3 Each processor stores local vertices & edges in a compressed row structure. Has been scaled to >108 vertices, >109 edges in interactive session.

Sparse Array and Matrix Operations • dsparse layout, same semantics as ordinary full & sparse • Matrix arithmetic: +, max, sum, etc. • matrix * matrix and matrix * vector • Matrix indexing and concatenation A (1: 3, [4 5 2]) = [ B(: , J) C ] ; 11 • Linear solvers: x = A b; using Super. LU (MPI) • Eigensolvers: [V, D] = eigs(A); using PARPACK (MPI)

Large-Scale Graph Algorithms 12 • Graph theory, algorithms, and data structures are ubiquitous in sparse matrix computation. • Time to turn the relationship around! • Represent a graph as a sparse adjacency matrix. • A sparse matrix language is a good start on primitives for computing with graphs. • Leverage the mature techniques and tools of highperformance numerical computation.

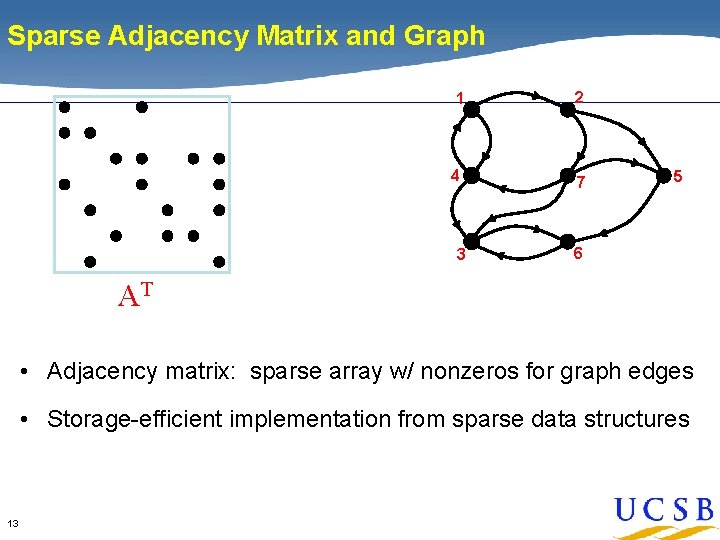
Sparse Adjacency Matrix and Graph 1 2 4 7 3 AT x 5 6 AT x • Adjacency matrix: sparse array w/ nonzeros for graph edges • Storage-efficient implementation from sparse data structures 13

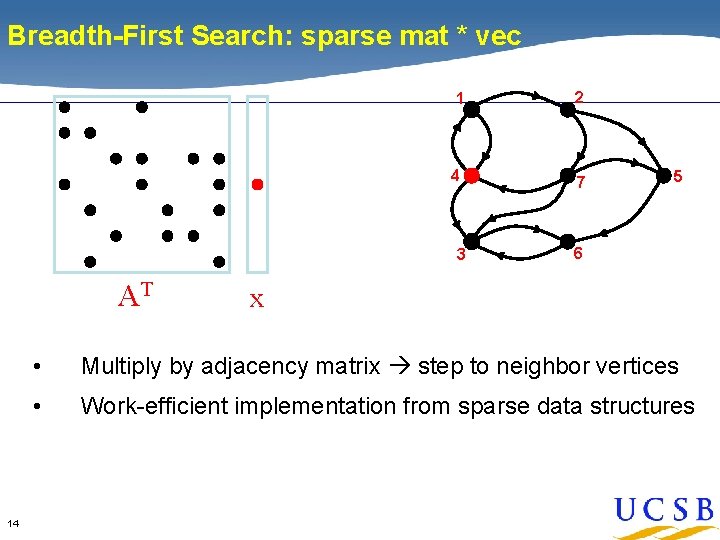
Breadth-First Search: sparse mat * vec 1 2 4 7 3 AT 14 x 5 6 AT x • Multiply by adjacency matrix step to neighbor vertices • Work-efficient implementation from sparse data structures

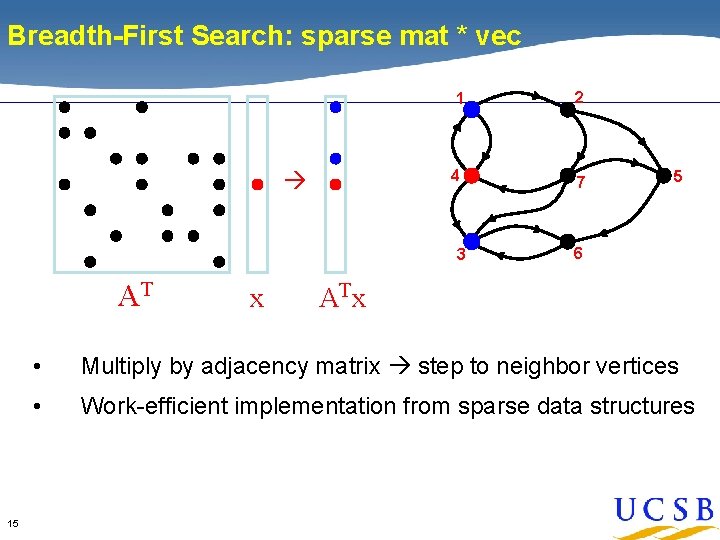
Breadth-First Search: sparse mat * vec 1 2 4 7 3 AT 15 x 5 6 AT x • Multiply by adjacency matrix step to neighbor vertices • Work-efficient implementation from sparse data structures

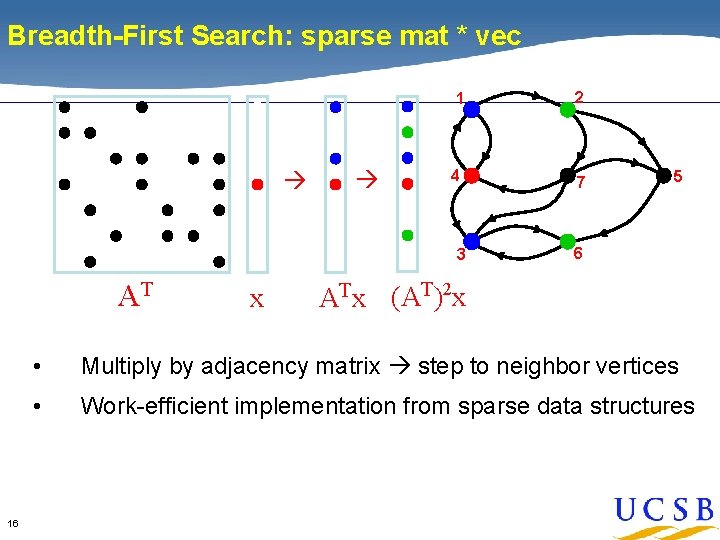
Breadth-First Search: sparse mat * vec 1 2 4 7 3 AT 16 x 5 6 ATx (AT)2 x • Multiply by adjacency matrix step to neighbor vertices • Work-efficient implementation from sparse data structures

HPCS Graph Clustering Benchmark Fine-grained, irregular data access Searching and clustering 17 • Many tight clusters, loosely interconnected • Input data is edge triples < i, j, label(i, j) > • Vertices and edges permuted randomly

Clustering by Breadth-First Search • Grow local clusters from many seeds in parallel • Breadth-first search by sparse matrix * matrix • Cluster vertices connected by many short paths % Grow each seed to vertices % reached by at least k % paths of length 1 or 2 C = sparse(seeds, 1: ns, 1, n, ns); C = A * C; C = C + A * C; C = C >= k; 18

Toolbox for Graph Analysis and Pattern Discovery Layer 1: Graph Theoretic Tools 19 • Graph operations • Global structure of graphs • Graph partitioning and clustering • Graph generators • Visualization and graphics • Scan and combining operations • Utilities

Typical Application Stack Computational ecology, CFD, data exploration Applications CG, Bi. CGStab, etc. + combinatorial preconditioners (AMG, Vaidya) Preconditioned Iterative Methods Graph querying & manipulation, connectivity, spanning trees, geometric partitioning, nested dissection, NNMF, . . . Graph Analysis & PD Toolbox Arithmetic, matrix multiplication, indexing, solvers (, eigs) Distributed Sparse Matrices 20

Landscape Connnectivity Modeling 21 • Landscape type and features facilitate or impede movement of members of a species • Different species have different criteria, scales, etc. • Habitat quality, gene flow, population stability • Corridor identification, conservation planning

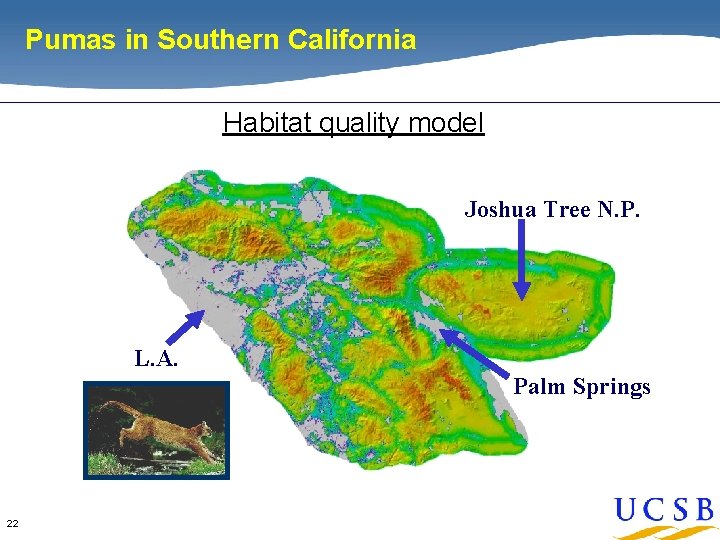
Pumas in Southern California Habitat quality model Joshua Tree N. P. L. A. Palm Springs 22

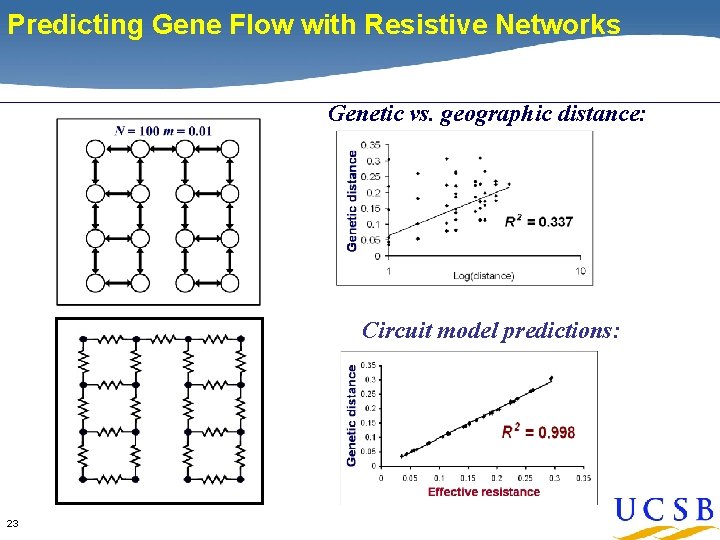
Predicting Gene Flow with Resistive Networks Genetic vs. geographic distance: Circuit model predictions: 23

Early Experience with Real Genetic Data • Good results with wolverines, mahogany, pumas • Matlab implementation • Needed: 24 – Finer resolution – Larger landscapes – Faster interaction 5 km resolution(too coarse)

Circuitscape: Combinatorics and Numerics • Model landscape (ideally at 100 m resolution for pumas). • Initial grid models connections to 4 or 8 neighbors. • Partition landscape into connected components via GAPDT • Use GAPDT to contract habitats into single graph nodes. • Compute resistance for pairs of habitats. • Direct methods are too slow for largest problems. • Use iterative solvers via Star-P: Hypre (PCG+AMG) 25

Parallel Circuitscape Results Pumas in southern California: – 12 million nodes – Under 1 hour (16 processors) – Original code took 3 days at coarser resolution Targeting much larger problems: – 26 Yellowstone-to-Yukon corridor Figures courtesy of Brad Mc. Rae, NCEAS

Sparse Matrix times Sparse Matrix • 27 A primitive in many array-based graph algorithms: – Parallel breadth-first search – Shortest paths – Graph contraction – Subgraph / submatrix indexing – Etc. • Graphs are often not mesh-like, i. e. geometric locality and good separators. • Often do not want to optimize for one repeated operation, as in matvec for iterative methods

Sparse Matrix times Sparse Matrix • 28 Current work: – Parallel algorithms with 2 D data layout – Sequential and parallel hypersparse algorithms – Matrices over semirings

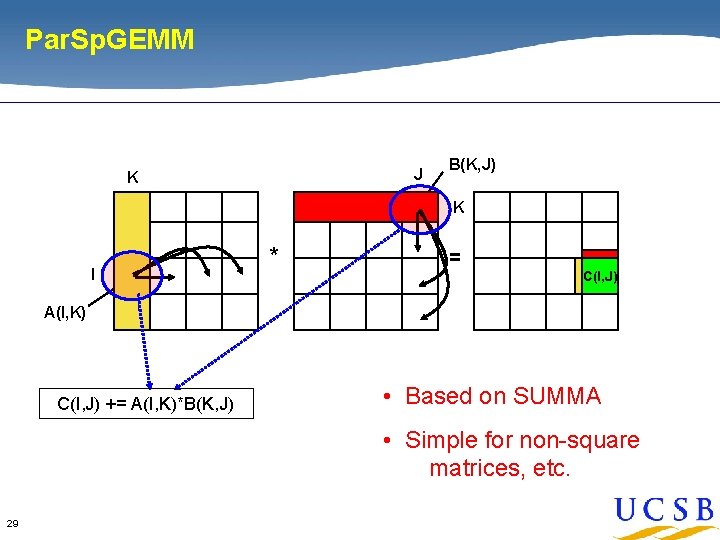
Par. Sp. GEMM J K B(K, J) K I * = C(I, J) A(I, K) C(I, J) += A(I, K)*B(K, J) • Based on SUMMA • Simple for non-square matrices, etc. 29

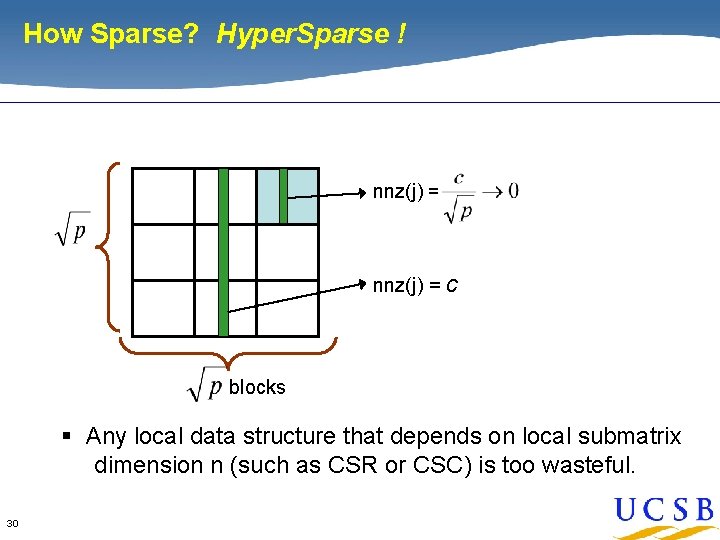
How Sparse? Hyper. Sparse ! nnz(j) = c blocks § Any local data structure that depends on local submatrix dimension n (such as CSR or CSC) is too wasteful. 30

Sparse. DComp Data Structure 31 • “Doubly compressed” data structure • Maintains both DCSC and DCSR • C = A*B needs only A. DCSC and B. DCSR • 4*nnz values communicated for A*B in the worst case (though we usually get away with much less)

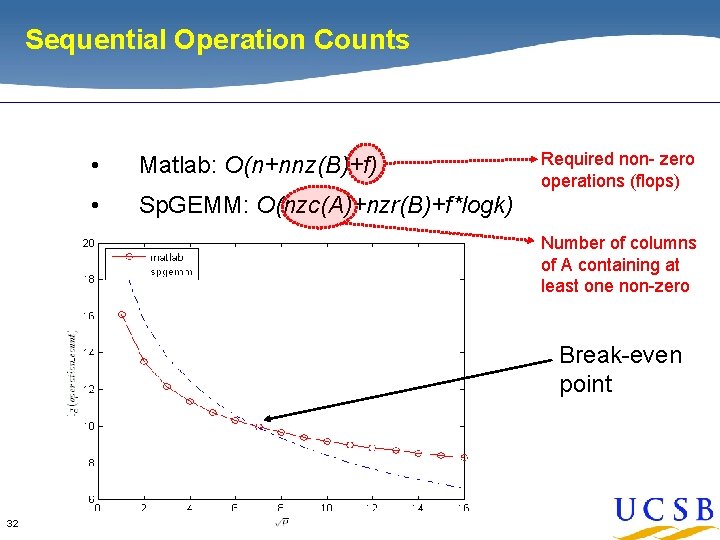
Sequential Operation Counts • Matlab: O(n+nnz(B)+f) • Sp. GEMM: O(nzc(A)+nzr(B)+f*logk) Required non- zero operations (flops) Number of columns of A containing at least one non-zero Break-even point 32

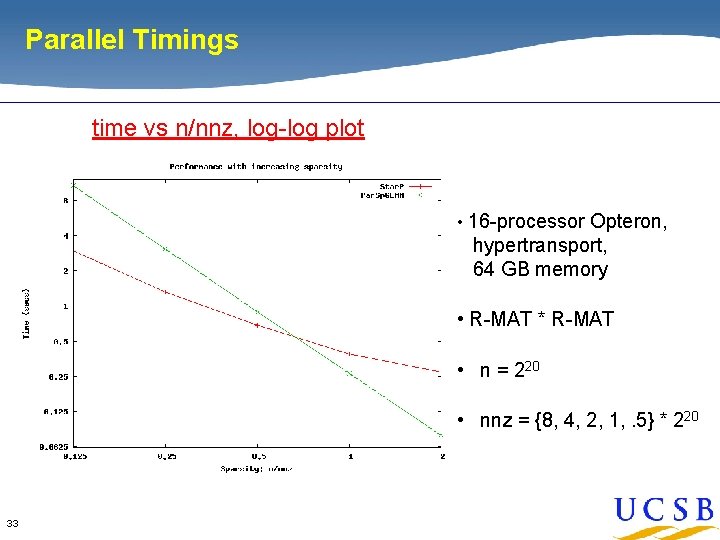
Parallel Timings time vs n/nnz, log-log plot • 16 -processor Opteron, hypertransport, 64 GB memory • R-MAT * R-MAT • n = 220 • nnz = {8, 4, 2, 1, . 5} * 220 33

Matrices over Semirings • Matrix multiplication C = AB (or matrix/vector): Ci, j = Ai, 1 B 1, j + Ai, 2 B 2, j + · · · + Ai, n Bn, j • Replace scalar operations and + by : associative, distributes over , identity 1 : associative, commutative, identity 0 annihilates under 34 • Then Ci, j = Ai, 1 B 1, j Ai, 2 B 2, j · · · Ai, n Bn, j • Examples: ( , +) ; (and, or) ; (+, min) ; . . . • Same data reference pattern and control flow

Remarks • Tools for combinatorial methods built on parallel sparse matrix infrastructure • Easy-to-use interactive programming environment – Rapid prototyping tool for algorithm development – Interactive exploration and visualization of data • Sparse matrix * sparse matrix is a key primitive • Matrices over semirings like (min, +) as well as (+, *) 35