Parallel solution of highfrequency Helmholtz equation using highorder

Parallel solution of high-frequency Helmholtz equation using highorder finite difference schemes Dan Gordon Rachel Gordon Computer Science University of Haifa Aerospace Eng. Technion July 2011 High-order schemes for high-frequency Helmholtz equation 1

Outline u Background u The on Helmholtz equation CARP-CG parallel algorithm u Comparative results using low- and high-order finite difference schemes July 2011 High-order schemes for high-frequency Helmholtz equation 2

The Helmholtz Equation Eqn: -Δu - k 2 u = g (k = "wave no. ") u c = speed of sound, f = frequency u Wave length: l = c/f = 2 p/k u No. of grid pts per l: Ng = l/h, h=mesh size u Shifted Laplacian approach: – Bayliss, Goldstein & Turkel, 1983 – Erlangga, Vuik & Oosterlee, 2004/06 introduced imaginary shift: -Δu – (1 - i b) k 2 u = f u July 2011 High-order schemes for high-frequency Helmholtz equation 3

The Helmholtz Equation u Some other approaches: – Elman, Ernst & O'Leary, 2001 – Plessix & Mulder, 2003 – Duff, Gratton, Pinel & Vasseeur, 2007 – Bollhöfer, Grote & Schenk, 2009 – Osei-Kuffuor & Saad, 2010 u This work: hi-order schemes following – Singer & Turkel, 2006 – Erlangga & Turkel, 2011 (to appear) July 2011 High-order schemes for high-frequency Helmholtz equation 4

Difficulties with Helmholtz u High frequencies small diagonal u 2 nd order schemes require many grid points/wavelength u "Pollution effect": high frequency requires more than fixed number of grid points/wavelength (Babuška & Sauter, 2000) u high-order schemes required July 2011 High-order schemes for high-frequency Helmholtz equation 5

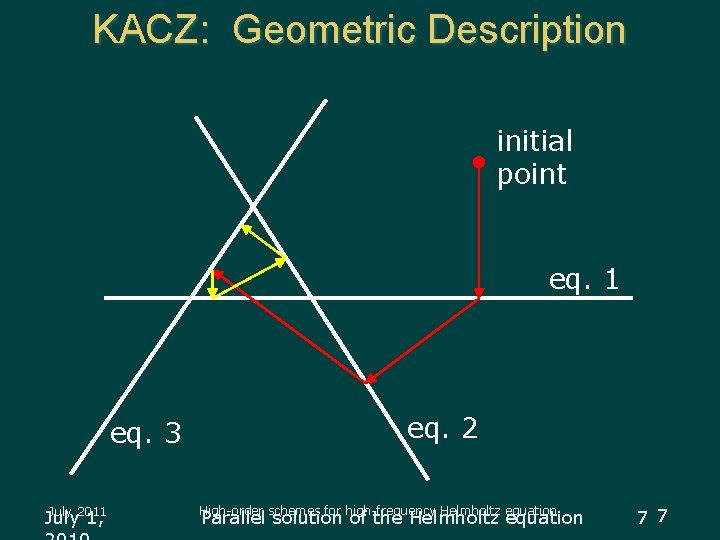
CARP: block-parallel Kaczmarz u Given: Ax=b u "Normal equations": AATy=b, x=ATy u Kaczmarz algorithm (1937) "KACZ" is SOR on normal equations u Relaxation parameter of KACZ is the usual relax. par. of SOR u Cyclic relax. par. : each eq. gets its own relax. par. July 2011 High-order schemes for high-frequency Helmholtz equation 6

KACZ: Geometric Description initial point eq. 1 eq. 3 July 2011 July 1, eq. 2 High-order schemes for high-frequency Helmholtz equation Parallel solution of the Helmholtz equation 7 7

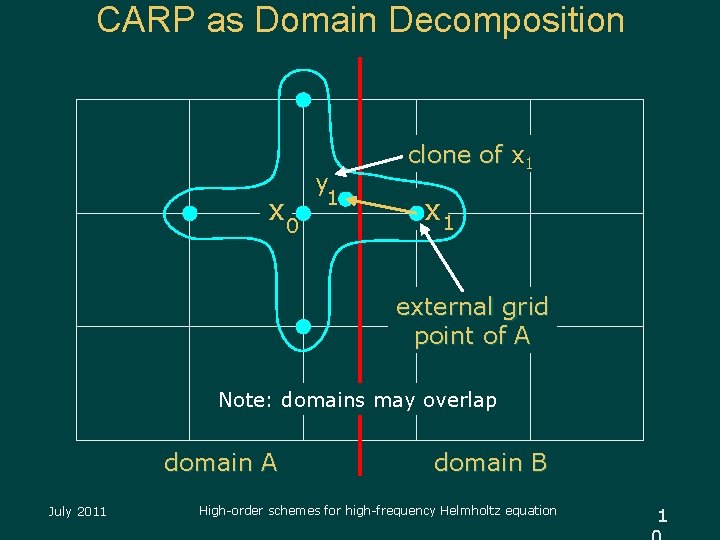
CARP: Component-Averaged Row Projections u. A block-parallel version of KACZ u Equations divided into blocks (not necessarily disjoint) u Initial estimate: vector x=(x 1, …, xn) u Suppose component x 1 appears in 3 blocks u x 1 is “cloned” as y 1 , z 1 , t 1 in the different blocks. u Perform a KACZ iteration on each block (independently, in parallel) July 2011 High-order schemes for high-frequency Helmholtz equation 8

CARP – Explanation (cont) u The internal iterations in each block produce 3 new values for the clones of x 1 : y 1’ , z 1’ , t 1’ u The next iterative value of x 1 is x 1’ = (y 1’ + z 1’ + t 1’)/3 u The next iterate is x’ = (x 1’ , . . . , xn’) u Repeat iterations as needed for convergence July 2011 High-order schemes for high-frequency Helmholtz equation 9

CARP as Domain Decomposition x 0 y 1 clone of x 1 external grid point of A Note: domains may overlap domain A July 2011 domain B High-order schemes for high-frequency Helmholtz equation 1

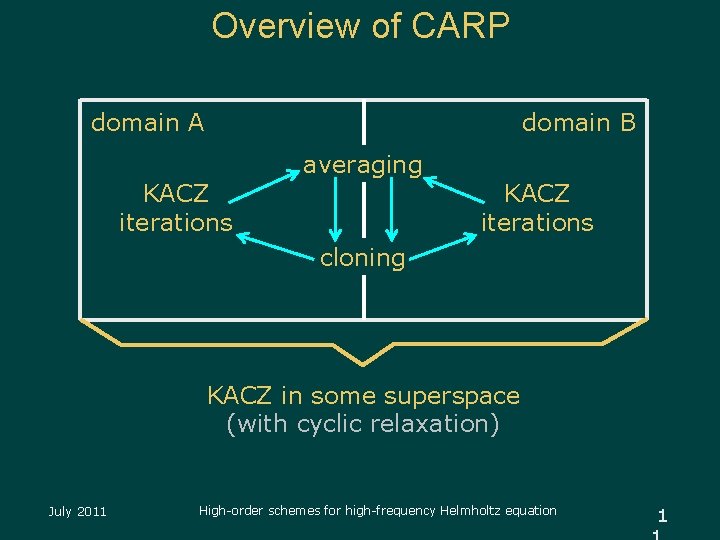
Overview of CARP domain A domain B KACZ iterations averaging KACZ iterations cloning KACZ in some superspace (with cyclic relaxation) July 2011 High-order schemes for high-frequency Helmholtz equation 1

Convergence of CARP u Averaging Lemma: the component- averaging operations of CARP are equivalent to KACZ row-projections in a certain superspace (with w=1) u CARP is equivalent to KACZ in the superspace, with cyclic relaxation parameters – known to converge July 2011 High-order schemes for high-frequency Helmholtz equation 1

CARP Applications u Elliptic PDEs w/large convection term result in stiff linear systems (large off -diagonal elements) – CARP very robust on such systems, compared to leading solver & preconditioner combinations – Downside: Not always efficient u Electron tomography (ET) – joint work with J. -J. Fernández July 2011 High-order schemes for high-frequency Helmholtz equation 1

CARP-CG: CG acceleration of CARP u CARP is KACZ in some superspace (with cyclic relaxation parameters) u Björck & Elfving (1979): developed CGMN, which is a (sequential) CGacceleration of KACZ (double sweep, fixed relax. parameter) u We extended this result to allow cyclic relaxation parameters u Result: CARP-CG July 2011 High-order schemes for high-frequency Helmholtz equation 1

CARP-CG: Properties u Same robustness as CARP u Very significant improvement in performance on stiff linear systems derived from elliptic PDEs u Very competitive runtime compared to leading solver/preconditioner combinations on systems derived from convection-dominated PDEs u Highly scalable on Helmholtz eqns July 2011 High-order schemes for high-frequency Helmholtz equation 1

CARP-CG: Properties u On one processor, CARP-CG is identical to CGMN u Particularly useful on systems with LARGE off-diagonal elements – example: convection-dominated PDEs u Discontinuous coefficients are handled without requiring domain decomposition (DD) July 2011 High-order schemes for high-frequency Helmholtz equation 1

Robustness of CARP-CG u KACZ inherently "normalizes" the eqns (eqn i is divided by ║Ai║ 2) u Normalization is generally useful for discontinuous coefficients u After normalization, the diagonal elements of AAT are all 1, and strictly greater than the off-diagonal elements u This is not diagonal dominance, but it makes the normal eqns manageable u Also: when diag of A decreases, sum of off-diag of AAT decreases. July 2011 High-order schemes for high-frequency Helmholtz equation 1

Experiments with Hi-Order u Relax. par. = 1. 5 for all problems u 2 nd, 4 th & 6 th order central difference schemes, following – Singer & Turkel, 2006 – Erlangga & Turkel, 2011 u Hi-order schemes 9 -pt. stencil u Complex eqns: separated real & imag. , interleaved equations (following Day & Heroux, 2001) July 2011 High-order schemes for high-frequency Helmholtz equation 1

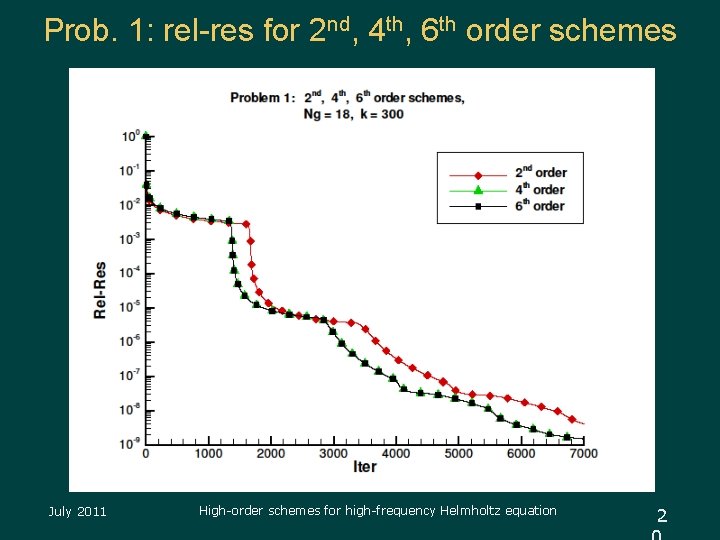
Problem 1 (with analytic sol'n) u u u Based on Erlangga & Turkel, 2011 Eqn: (Δ+k 2)u = 0, on [-0. 5, 0. 5] [0, 1] bndry condition: Dirichlet on 3 sides: – u=0 for x=-0. 5 and x=0. 5 – u=cos(px) for y=0 – Sommerfeld: uy+iβu=0 for y=1, β 2=k 2 -p 2 u u u Analytic solution: u = cos(px)exp(-iβy) Grid points per l: Ng = 9, 12, 15, 18 Approx. 186, 000 – 742, 000 complex variables One processor k = 300 July 2011 High-order schemes for high-frequency Helmholtz equation 1

Prob. 1: rel-res for 2 nd, 4 th, 6 th order schemes July 2011 High-order schemes for high-frequency Helmholtz equation 2

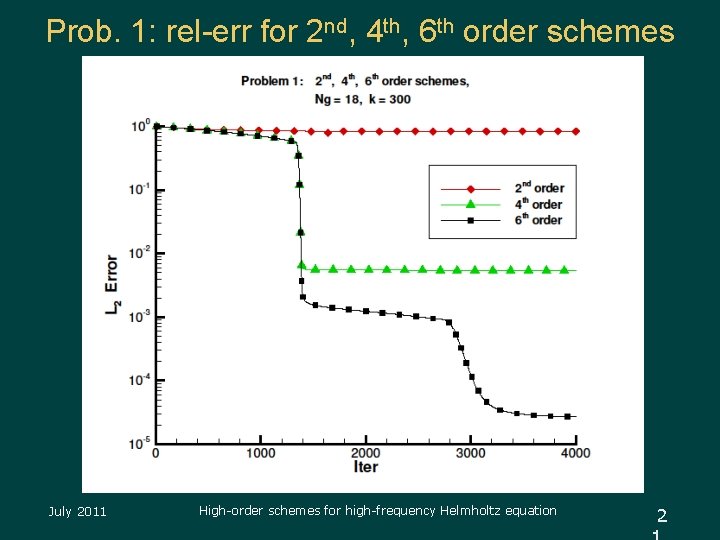
Prob. 1: rel-err for 2 nd, 4 th, 6 th order schemes July 2011 High-order schemes for high-frequency Helmholtz equation 2

Prob. 1: rel-err for 2 nd, 4 th, 6 th order schemes July 2011 High-order schemes for high-frequency Helmholtz equation 2

Problem 2 (with analytic soln) u u u u u Eqn: Δu + k 2 u = 0 Domain: [0, 1] Analytic sol'n: u=sin(px)cos(βy), β 2=k 2 -p 2 Dirichlet bndry cond determined by u on the boundaries Grid points per l: Ng = 9 to 18 Approx. 186, 000 – 742, 000 real variables One processor k = 300 2 nd, 4 th, 6 th order schemes July 2011 High-order schemes for high-frequency Helmholtz equation 2

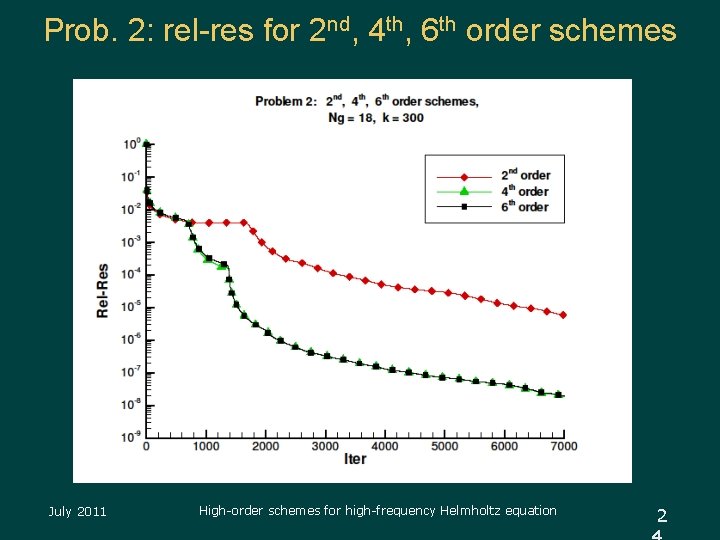
Prob. 2: rel-res for 2 nd, 4 th, 6 th order schemes July 2011 High-order schemes for high-frequency Helmholtz equation 2

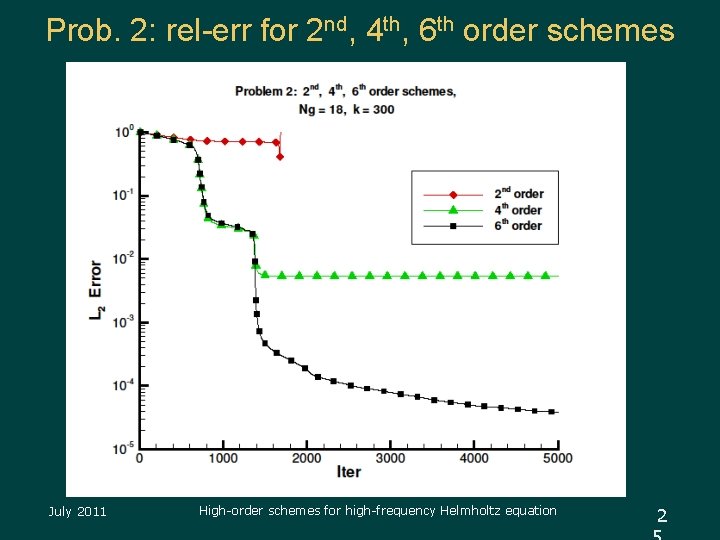
Prob. 2: rel-err for 2 nd, 4 th, 6 th order schemes July 2011 High-order schemes for high-frequency Helmholtz equation 2

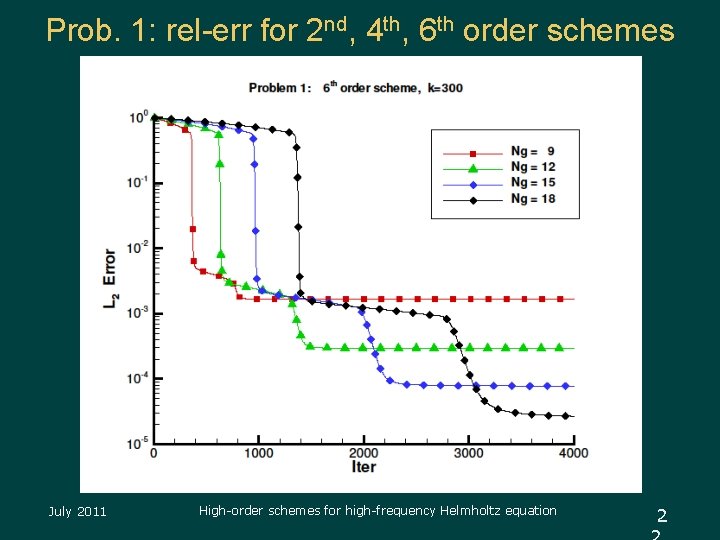
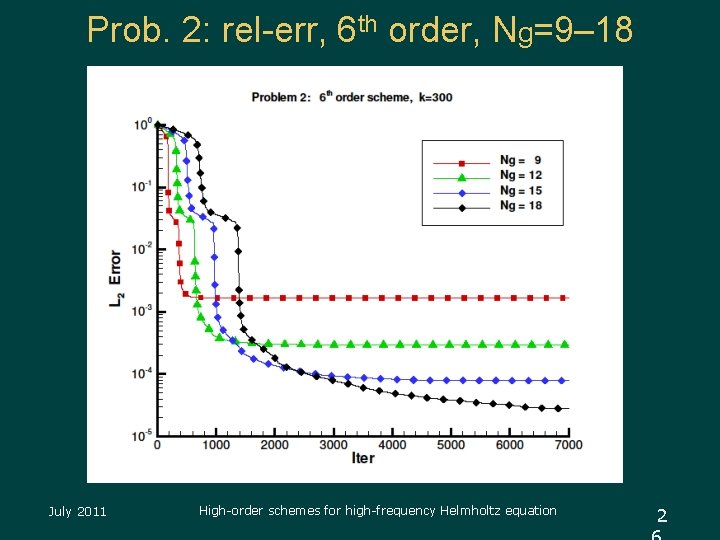
Prob. 2: rel-err, 6 th order, Ng=9– 18 July 2011 High-order schemes for high-frequency Helmholtz equation 2

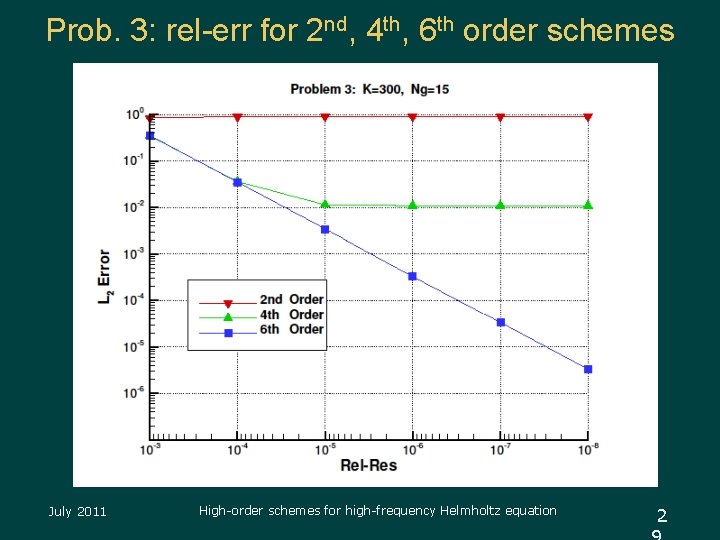
Problem 3 (no analytic soln) u Eqn: Δu + k 2 u = 0 Domain: [0, 1] u Bndry cond on y=0: discontinuity at midpt. : u(0. 5, 0)=1, u(x, 0) = 0 for x ≠ 0 other sides: 1 st order absorbing u Approx. 515, 000 complex variables u Grid points per l: Ng = 15 u One processor u k = 300 u 2 nd, 4 th, 6 th order schemes u July 2011 High-order schemes for high-frequency Helmholtz equation 2

Problem 3: evaluating the error u No analytic solution u Run 6 th order scheme to rel-res=10 -13 u Saved result as “true” solution u Compared results of 2 nd, 4 th and 6 th order schemes with the “true” solution July 2011 High-order schemes for high-frequency Helmholtz equation 2

Prob. 3: rel-err for 2 nd, 4 th, 6 th order schemes July 2011 High-order schemes for high-frequency Helmholtz equation 2

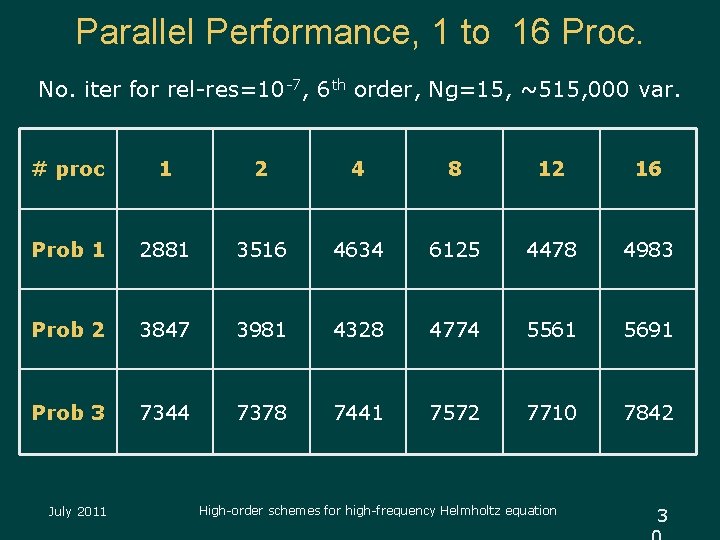
Parallel Performance, 1 to 16 Proc. No. iter for rel-res=10 -7, 6 th order, Ng=15, ~515, 000 var. # proc 1 2 4 8 12 16 Prob 1 2881 3516 4634 6125 4478 4983 Prob 2 3847 3981 4328 4774 5561 5691 Prob 3 7344 7378 7441 7572 7710 7842 July 2011 High-order schemes for high-frequency Helmholtz equation 3

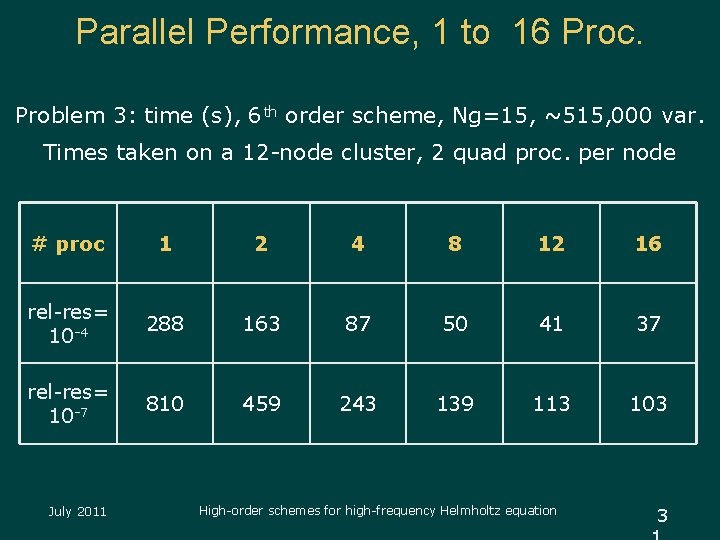
Parallel Performance, 1 to 16 Proc. Problem 3: time (s), 6 th order scheme, Ng=15, ~515, 000 var. Times taken on a 12 -node cluster, 2 quad proc. per node # proc 1 2 4 8 12 16 rel-res= 10 -4 288 163 87 50 41 37 rel-res= 10 -7 810 459 243 139 113 103 July 2011 High-order schemes for high-frequency Helmholtz equation 3

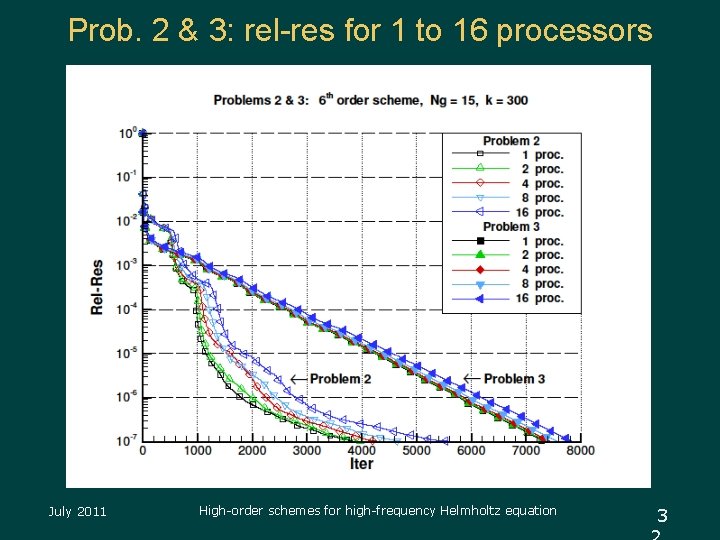
Prob. 2 & 3: rel-res for 1 to 16 processors July 2011 High-order schemes for high-frequency Helmholtz equation 3

Summary u Hi-freq Helmholtz require hi-order schemes u CARP-CG is applicable to hi-freq Helmholtz with hi-order schemes u Parallel and simple u General-purpose – for problems with large off-diagonal elements and discontinuous coefficients July 2011 High-order schemes for high-frequency Helmholtz equation 3

Other Potential Applications u Hi-order schemes for Helmholtz in homog & heterog 3 D domains u Maxwell equations u Other physics equations u Saddle-point problems u Circuit problems u Linear solver in some eigenvalue methods July 2011 High-order schemes for high-frequency Helmholtz equation 3

Publications and Software http: //cs. haifa. ac. il/~gordon/pub. html CARP: SIAM J Sci Comp 2005 CGMN: ACM Trans Math Software 2008 Microscopy: J Parallel & Distr Comp 2008 Large convection + discont coef: CMES 2009 CARP-CG: Parallel Comp 2010 Normalization for discont coef: J Comp & Appl Math 2010 CARP-CG software: http: //cs. haifa. ac. il/~gordon/soft. html THANK YOU! July 2011 High-order schemes for high-frequency Helmholtz equation 3