Parallel Programming Techniques and Applications Using Networked Workstations

Parallel Programming: Techniques and Applications Using Networked Workstations and Parallel Computers Barry Wilkinson and Michael Allen Chapter 11: Numerical Algorithms Sec 11. 2: Implementing Matrix Multiplication Modified 5/11/05 by T. O’Neil for 3460: 4/577, Fall 2005, Univ. of Akron. Previous revision: 7/28/03. (c) Prentice-Hall Inc. , 2002. All rights reserved.

Implementing Matrix Multiplication Sequential Code Assume throughout that the matrices are square (n n matrices). The sequential code to compute A B could simply be for (i=0; i<n; i++) for (j=0; j<n; j++) { c[i][j] = 0; for (k=0; k<n; k++) c[i][j] = c[i][j] + a[i][k]* b[k][j]; } This algorithm requires n 3 multiplications and n 3 additions, leading to a sequential time complexity of O(n 3). Very easy to parallelize. Wilkinson & Allen, Parallel Programming: Techniques & Applications Using Networked Workstations & Parallel Computers, 1999. 2

Parallel Code With n processors (and n n matrices), can obtain: • Time complexity of O(n 2) with n processors Each instance of inner loop independent and can be done by a separate processor. Cost optimal since O(n 3)=n O(n 2). • Time complexity of O(n) with n 2 processors One element of A and B assigned to each processor. Cost optimal since O(n 3)=n 2 O(n). • Time complexity of O(log n) with n 3 processors By parallelizing the inner loop. Not cost-optimal since O(n 3) n 3 O(log n) lower bound for parallel matrix multiplication. Wilkinson & Allen, Parallel Programming: Techniques & Applications Using Networked Workstations & Parallel Computers, 1999. 3

Partitioning into Submatrices Suppose matrix divided into s 2 submatrices. Each submatrix has n/s elements. Using notation Ap, q as submatrix in submatrix row p and submatrix column q: for (p=0; p<s; p++) for (q=0; q<s; q++) { /* clear elements of submatrix */ Cp, q = 0; /* submatrix mult and */ /* add to accum submatrix */ for (r=0; r<m; r++) Cp, q = Cp, q + Ap, r * Br, q; } Wilkinson & Allen, Parallel Programming: Techniques & Applications Using Networked Workstations & Parallel Computers, 1999. 4

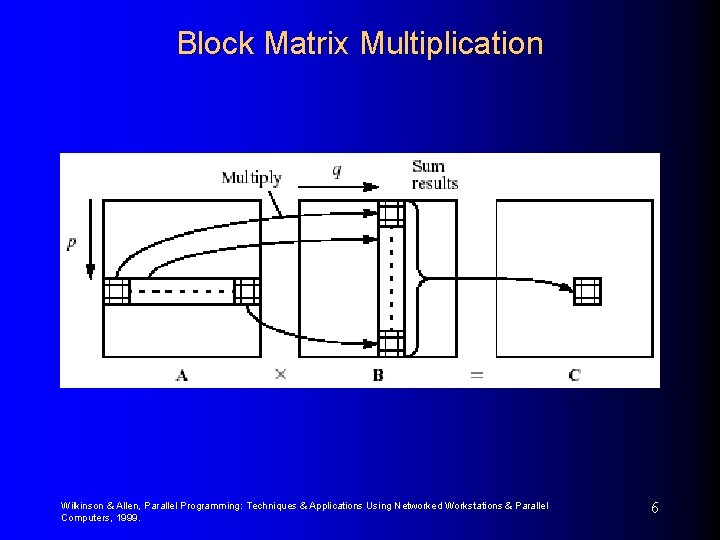
Partitioning into Submatrices (cont) for (p=0; p<s; p++) for (q=0; q<s; q++) { Cp, q = 0; for (r=0; r<m; r++) Cp, q = Cp, q + Ap, r * Br, q; } The line Cp, q=Cp, q+Ap, r*Br, q; means multiply submatrix Ap, r by Br, q using matrix multiplication and add to submatrix Cp, q using matrix addition. Known as block matrix multiplication. Wilkinson & Allen, Parallel Programming: Techniques & Applications Using Networked Workstations & Parallel Computers, 1999. 5

Block Matrix Multiplication Wilkinson & Allen, Parallel Programming: Techniques & Applications Using Networked Workstations & Parallel Computers, 1999. 6

Submatrix multiplication Matrices Wilkinson & Allen, Parallel Programming: Techniques & Applications Using Networked Workstations & Parallel Computers, 1999. 7

Submatrix multiplication Multiplying A 0, 0 B 0, 0 to obtain C 0, 0 Wilkinson & Allen, Parallel Programming: Techniques & Applications Using Networked Workstations & Parallel Computers, 1999. 8

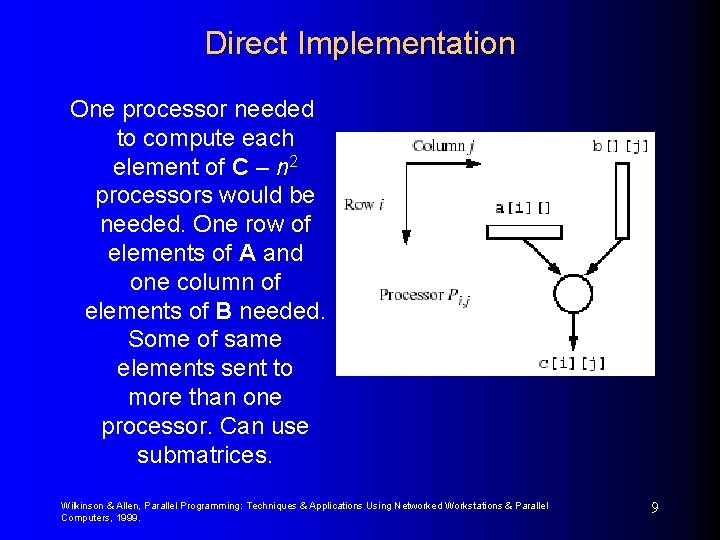
Direct Implementation One processor needed to compute each element of C – n 2 processors would be needed. One row of elements of A and one column of elements of B needed. Some of same elements sent to more than one processor. Can use submatrices. Wilkinson & Allen, Parallel Programming: Techniques & Applications Using Networked Workstations & Parallel Computers, 1999. 9

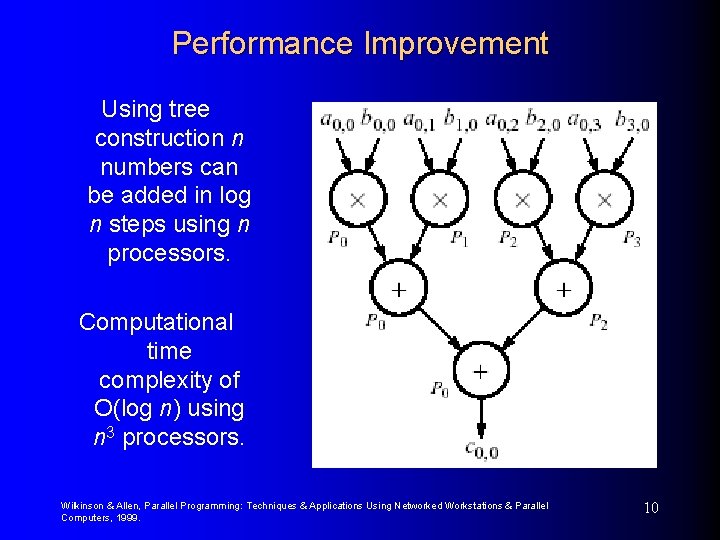
Performance Improvement Using tree construction n numbers can be added in log n steps using n processors. Computational time complexity of O(log n) using n 3 processors. Wilkinson & Allen, Parallel Programming: Techniques & Applications Using Networked Workstations & Parallel Computers, 1999. 10

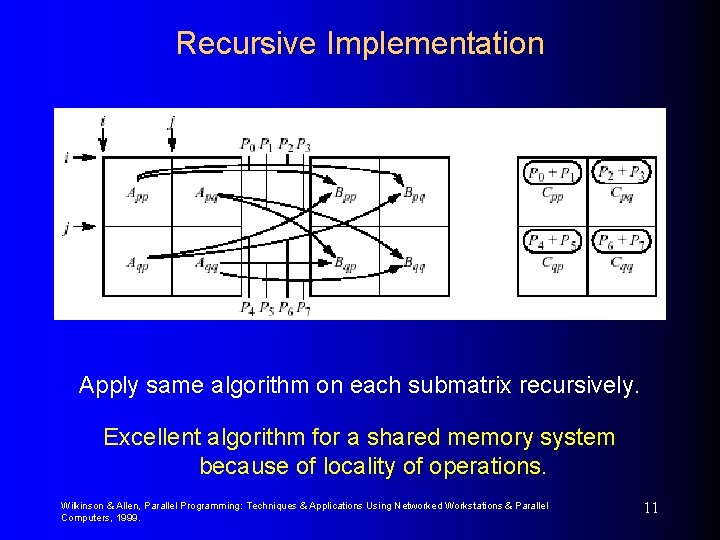
Recursive Implementation Apply same algorithm on each submatrix recursively. Excellent algorithm for a shared memory system because of locality of operations. Wilkinson & Allen, Parallel Programming: Techniques & Applications Using Networked Workstations & Parallel Computers, 1999. 11

Recursive Algorithm mat_mult(App, Bpp, s) { /* if submatrix has one elt multiply */ if (s==1) C = A*B; /* continue to make recursive calls */ else { s = s/2; /* no elts in each row/column */ P 0 = mat_mult(App, Bpp, s); P 1 = mat_mult(Apq, Bqp, s); P 2 = mat_mult(App, Bpq, s); P 3 = mat_mult(Apq, Bqq, s); Wilkinson & Allen, Parallel Programming: Techniques & Applications Using Networked Workstations & Parallel Computers, 1999. 12

Recursive Algorithm (cont) P 4 P 5 P 6 P 7 /* /* Cpp Cpq Cqp Cqq = mat_mult(Aqp, Bpp, s); = mat_mult(Aqq, Bqp, s); = mat_mult(Aqp, Bpq, s); = mat_mult(Aqq, Bqq, s); add submatrix products to form */ submatrices of final matrix */ = P 0 + P 1; = P 2 + P 3; = P 4 + P 5; = P 6 + P 7; } return(C); /* return final matrix */ } Wilkinson & Allen, Parallel Programming: Techniques & Applications Using Networked Workstations & Parallel Computers, 1999. 13

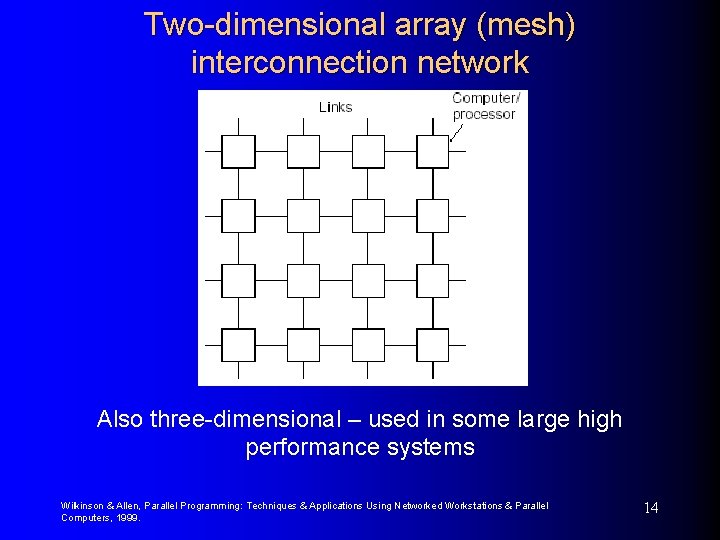
Two-dimensional array (mesh) interconnection network Also three-dimensional – used in some large high performance systems Wilkinson & Allen, Parallel Programming: Techniques & Applications Using Networked Workstations & Parallel Computers, 1999. 14

Mesh Implementations • Cannon’s algorithm • Fox’s algorithm • Not in textbook but similar complexity • Systolic array All involve using processors arranged in a mesh and shifting elements of the arrays through the mesh. Accumulate the partial sums at each processor. Wilkinson & Allen, Parallel Programming: Techniques & Applications Using Networked Workstations & Parallel Computers, 1999. 15

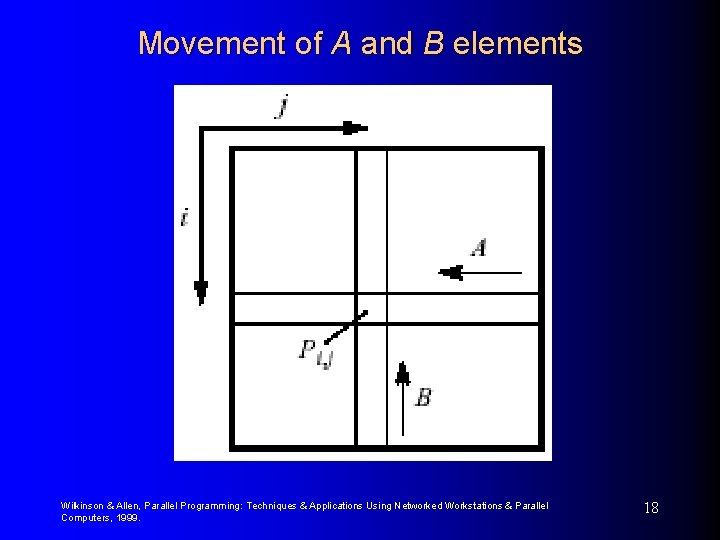
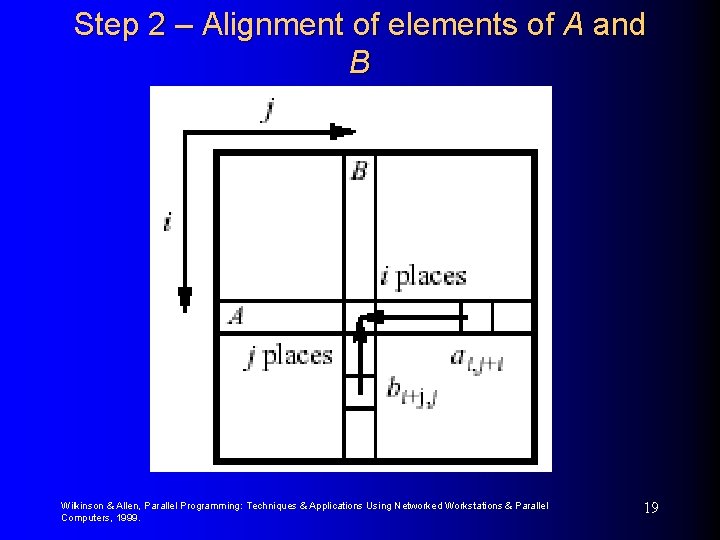
Mesh Implementations Cannon’s Algorithm Uses a mesh of processors with wraparound connections (a torus) to shift the A elements (or submatrices) left and the B elements (or submatrices) up. 1. Initially processor Pi, j has elements ai, j and bi, j (0 i, k<n). 2. Elements are moved from their initial position to an “aligned” position. The complete ith row of A is shifted i places left and the complete jth column of B is shifted j places upward. This has the effect of placing the element ai, j+i and the element bi+j, j in processor Pi, j. These elements are a pair of those required in the accumulation of ci, j. Wilkinson & Allen, Parallel Programming: Techniques & Applications Using Networked Workstations & Parallel Computers, 1999. 16

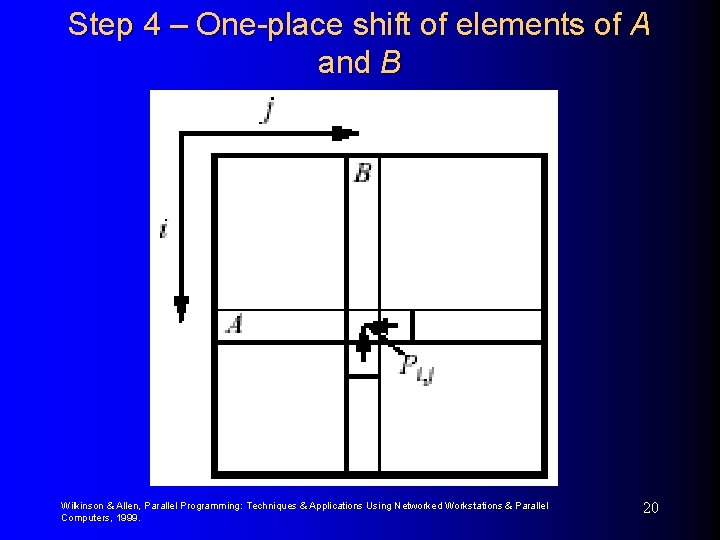
Mesh Implementations Cannon’s Algorithm (cont) 3. Each processor Pi, j multiplies its elements. 4. The ith row of A is shifted one place left, and the jth column of B is shifted one place upward. This has the effect of bringing together the adjacent elements of A and B, which will also be required in the accumulation. 5. Each processor Pi, j multiplies the elements brought to it and adds the result to the accumulating sum. 6. Steps 4 and 5 are repeated until the final result is obtained (n-1 shifts with n rows and n columns of elements). Wilkinson & Allen, Parallel Programming: Techniques & Applications Using Networked Workstations & Parallel Computers, 1999. 17

Movement of A and B elements Wilkinson & Allen, Parallel Programming: Techniques & Applications Using Networked Workstations & Parallel Computers, 1999. 18

Step 2 – Alignment of elements of A and B Wilkinson & Allen, Parallel Programming: Techniques & Applications Using Networked Workstations & Parallel Computers, 1999. 19

Step 4 – One-place shift of elements of A and B Wilkinson & Allen, Parallel Programming: Techniques & Applications Using Networked Workstations & Parallel Computers, 1999. 20

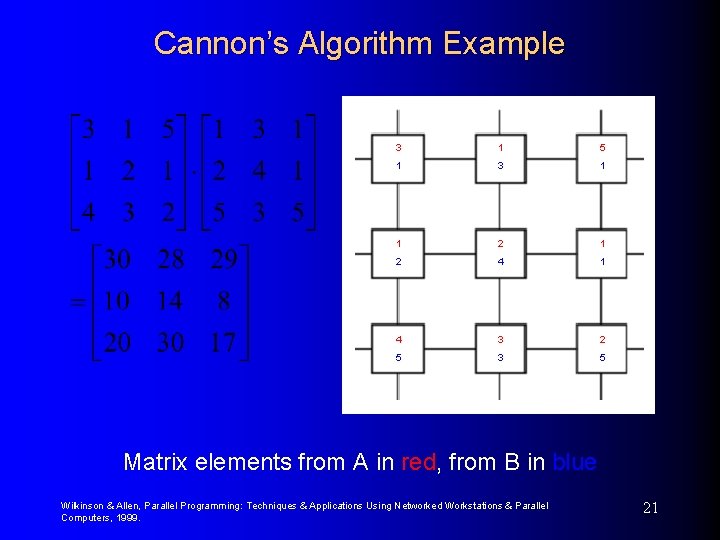
Cannon’s Algorithm Example 3 1 5 1 3 1 1 2 4 1 4 3 2 5 3 5 Matrix elements from A in red, from B in blue Wilkinson & Allen, Parallel Programming: Techniques & Applications Using Networked Workstations & Parallel Computers, 1999. 21

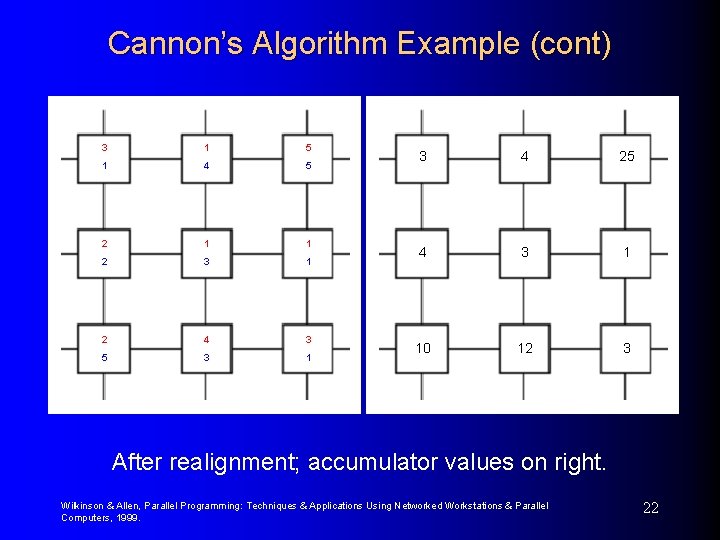
Cannon’s Algorithm Example (cont) 3 1 5 1 4 5 2 1 1 2 3 1 2 4 3 5 3 1 3 4 25 4 3 1 10 12 3 After realignment; accumulator values on right. Wilkinson & Allen, Parallel Programming: Techniques & Applications Using Networked Workstations & Parallel Computers, 1999. 22

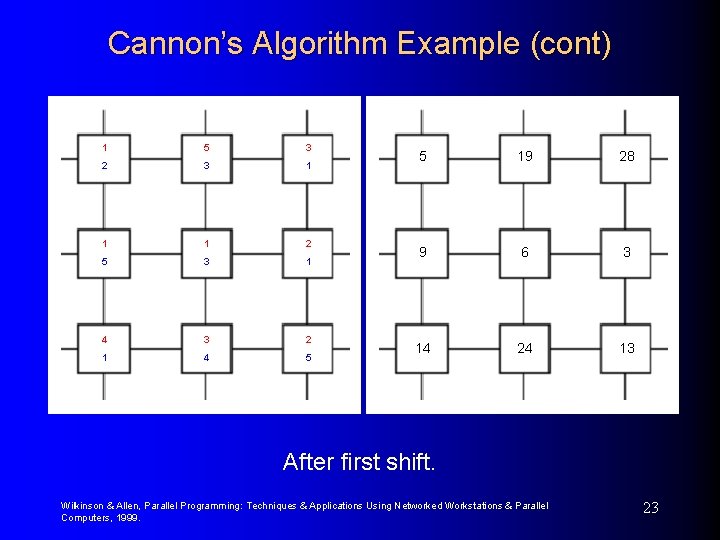
Cannon’s Algorithm Example (cont) 1 5 3 2 3 1 1 1 2 5 3 1 4 3 2 1 4 5 5 19 28 9 6 3 14 24 13 After first shift. Wilkinson & Allen, Parallel Programming: Techniques & Applications Using Networked Workstations & Parallel Computers, 1999. 23

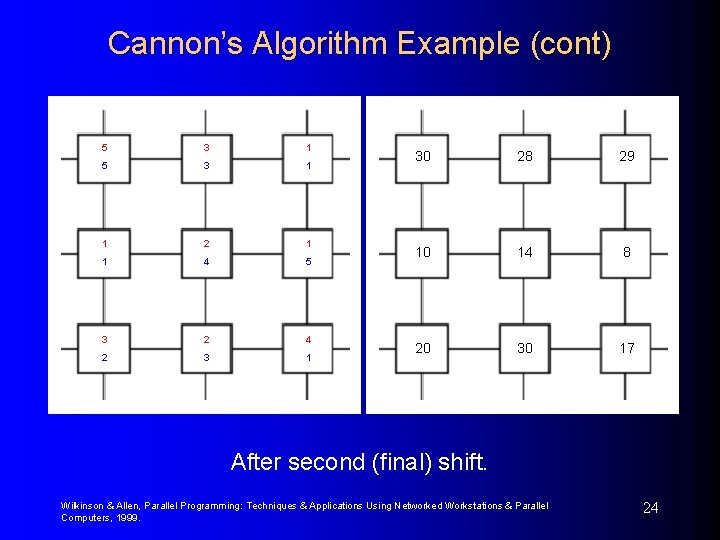
Cannon’s Algorithm Example (cont) 5 3 1 1 2 1 1 4 5 3 2 4 2 3 1 30 28 29 10 14 8 20 30 17 After second (final) shift. Wilkinson & Allen, Parallel Programming: Techniques & Applications Using Networked Workstations & Parallel Computers, 1999. 24

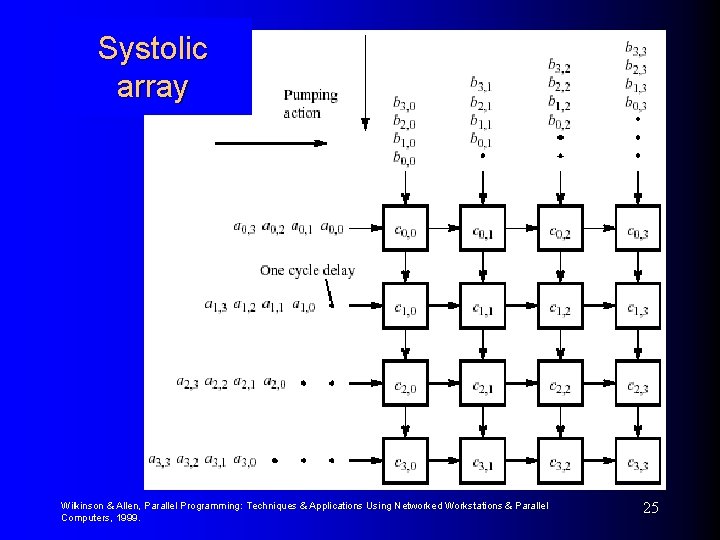
Systolic array Wilkinson & Allen, Parallel Programming: Techniques & Applications Using Networked Workstations & Parallel Computers, 1999. 25

Pseudocode Each processor Pi, j repeatedly performs the same algorithm (after c is initialized to zero): recv(&a, Pi, j-1); recv(&b, Pi-1, j); c = c + a * b; send(&a, Pi, j+1); send(&b, Pi+1, j); /* /* /* receive from left */ receive from above */ accumulate value */ send right */ send downwards */ which accumulates the required summations. Wilkinson & Allen, Parallel Programming: Techniques & Applications Using Networked Workstations & Parallel Computers, 1999. 26

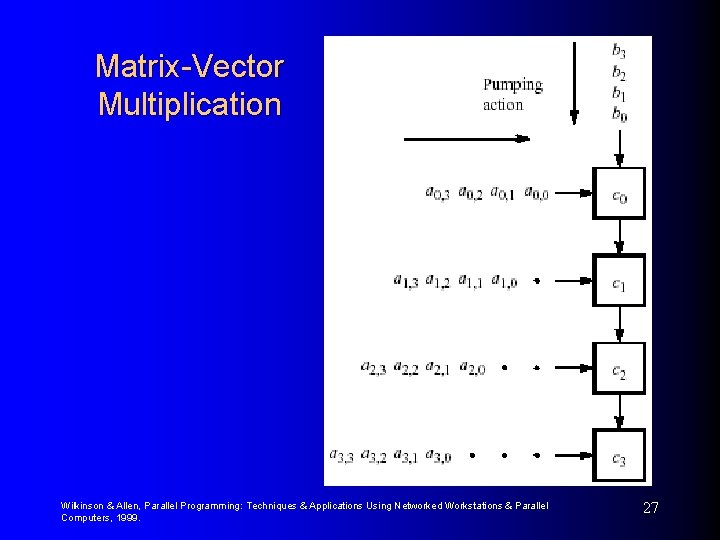
Matrix-Vector Multiplication Wilkinson & Allen, Parallel Programming: Techniques & Applications Using Networked Workstations & Parallel Computers, 1999. 27

Other Matrix Multiplication Methods Strassen’s method (1969) Suppose we wish to multiply n n matrices A and B to produce C. Divide each of these into four n/2 submatrices as follows: Wilkinson & Allen, Parallel Programming: Techniques & Applications Using Networked Workstations & Parallel Computers, 1999. 28

Strassen’s Method (cont) A traditional recursive approach executes in O(n 3) time so no faster. Strassen discovered a different recursive approach that executes in O(nlog 7) time: 1. Divide the input matrices into quarters as above. 2. Use O(n 2) scalar additions and subtractions to recursively compute seven matrix products Q 1 through Q 7. 3. Compute the desired submatrices of C by adding and/or subtracting various combinations of the Qi matrices, using O(n 2) scalar operations. Wilkinson & Allen, Parallel Programming: Techniques & Applications Using Networked Workstations & Parallel Computers, 1999. 29

Strassen’s Method (cont) To this end set • Q 1 = (A 11 + A 22)·(B 11 + B 22) • Q 2 = (A 21 + A 22)·B 11 • Q 3 = A 11·(B 12 – B 22) • Q 4 = A 22·(B 21 – B 11) • Q 5 = (A 11 + A 12)·B 22 • Q 6 = (A 21 – A 11)·(B 21 + B 22) • Q 7 = (A 12 – A 22)·(B 21 + B 22) As indicated above can be done recursively. Wilkinson & Allen, Parallel Programming: Techniques & Applications Using Networked Workstations & Parallel Computers, 1999. 30

Strassen’s Method (cont) Now • C 11 = Q 1 + Q 4 – Q 5 + Q 7 • C 21 = Q 2 + Q 4 • C 12 = Q 3 + Q 5 • C 22 = Q 1 + Q 3 – Q 2 + Q 6 Wilkinson & Allen, Parallel Programming: Techniques & Applications Using Networked Workstations & Parallel Computers, 1999. 31