Parallel Lines and Planes You will learn to

Parallel Lines and Planes You will learn to describe relationships among lines, parts of lines, and planes. In geometry, two lines in a plane that are always the same parallel lines distance apart are ______. No two parallel lines intersect, no matter how far you extend them.

Parallel Lines and Planes Definition of Parallel Lines Two lines are parallel iff they are in the same plane and intersect do not ____.

Parallel Lines and Planes can also be parallel. The shelves of a bookcase are examples of parts of planes. The shelves are the same distance apart at all points, and do not appear to intersect. parallel They are _______. parallel planes In geometry, planes that do not intersect are called _______. Q R Plane PSR || plane JML Plane JPQ || plane MLR Plane PJM || plane QRL P J K S L M

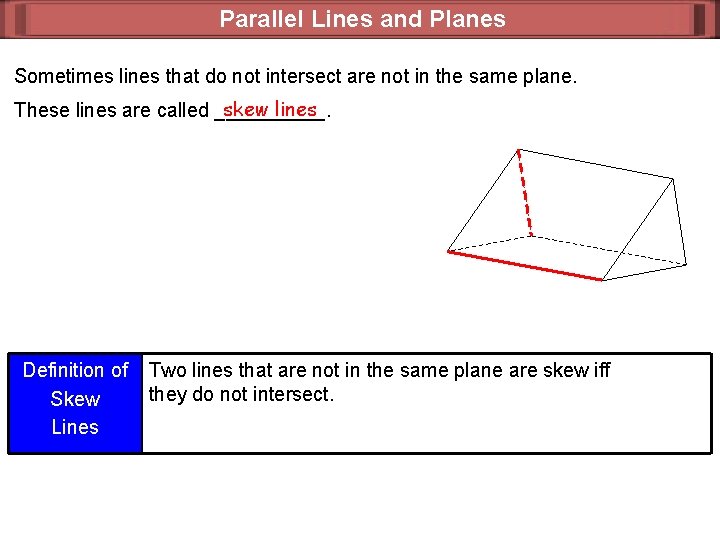
Parallel Lines and Planes Sometimes lines that do not intersect are not in the same plane. skew lines These lines are called _____. Definition of Skew Lines Two lines that are not in the same plane are skew iff they do not intersect.

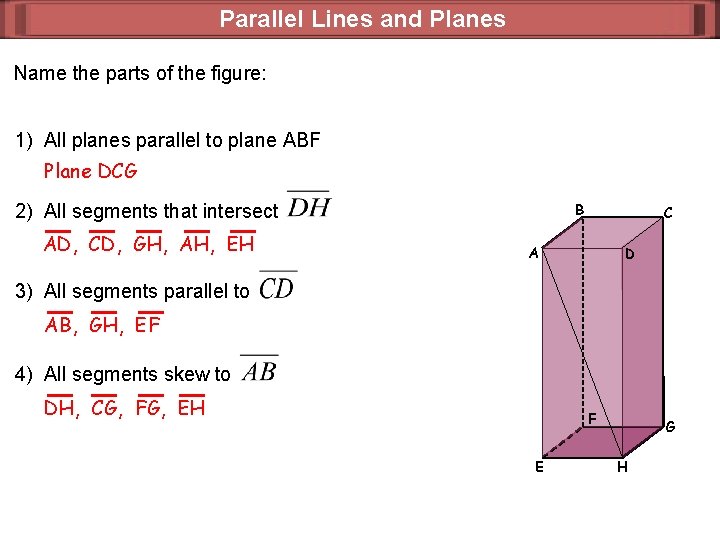
Parallel Lines and Planes Name the parts of the figure: 1) All planes parallel to plane ABF Plane DCG 2) All segments that intersect AD, CD, GH, AH, EH B C A D 3) All segments parallel to AB, GH, EF 4) All segments skew to DH, CG, FG, EH F E G H

Parallel Lines and Transversals You will learn to identify the relationships among pairs of interior and exterior angles formed by two parallel lines and a transversal.

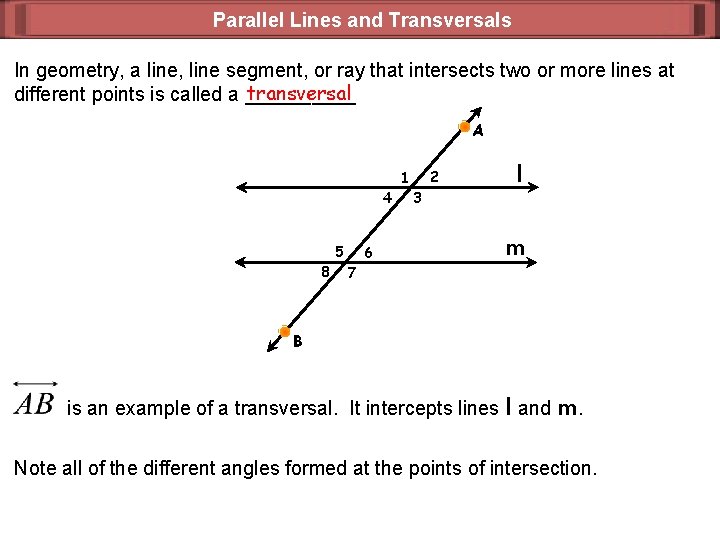
Parallel Lines and Transversals In geometry, a line, line segment, or ray that intersects two or more lines at transversal different points is called a _____ A 2 1 4 5 8 6 7 3 l m B is an example of a transversal. It intercepts lines l and m. Note all of the different angles formed at the points of intersection.

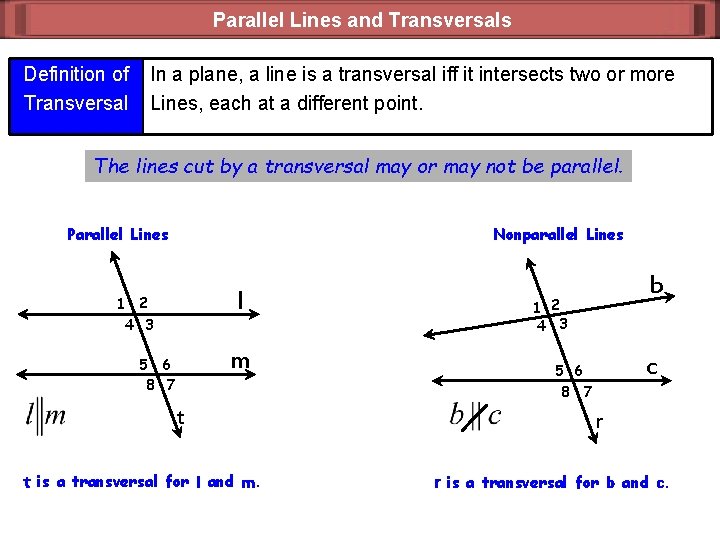
Parallel Lines and Transversals Definition of Transversal In a plane, a line is a transversal iff it intersects two or more Lines, each at a different point. The lines cut by a transversal may or may not be parallel. Parallel Lines Nonparallel Lines l 1 2 4 3 m 5 6 8 7 is a transversal for l and m. c 5 6 8 7 t t b r r is a transversal for b and c.

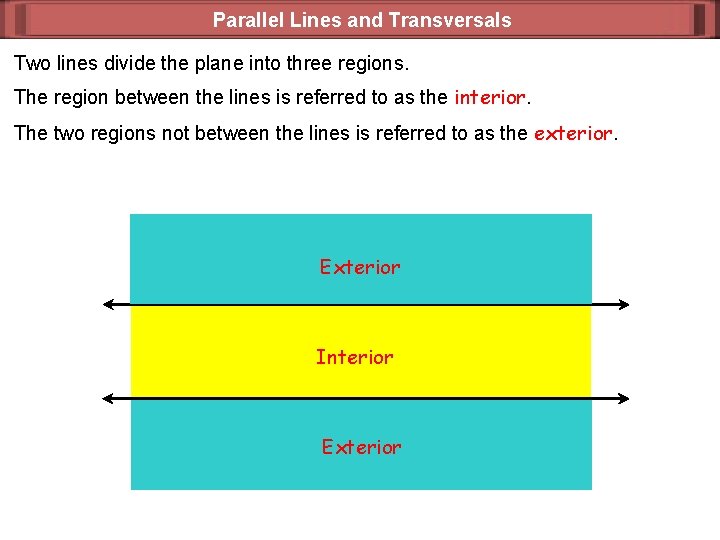
Parallel Lines and Transversals Two lines divide the plane into three regions. The region between the lines is referred to as the interior. The two regions not between the lines is referred to as the exterior. Exterior Interior Exterior

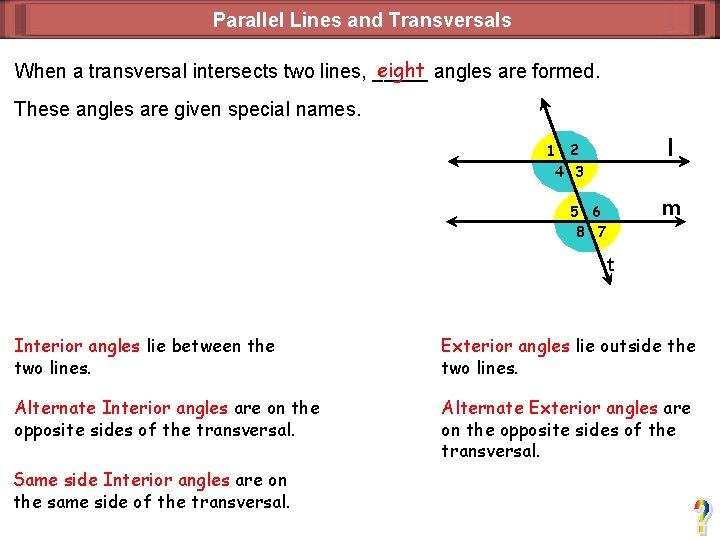
Parallel Lines and Transversals eight angles are formed. When a transversal intersects two lines, _____ These angles are given special names. l 1 2 4 3 m 5 6 8 7 t Interior angles lie between the two lines. Exterior angles lie outside the two lines. Alternate Interior angles are on the opposite sides of the transversal. Alternate Exterior angles are on the opposite sides of the transversal. Same side Interior angles are on the same side of the transversal.

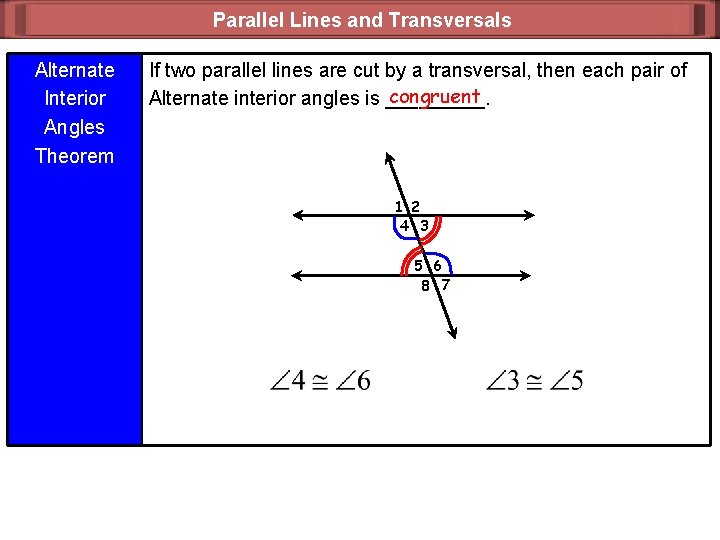
Parallel Lines and Transversals Alternate Interior Angles Theorem If two parallel lines are cut by a transversal, then each pair of congruent Alternate interior angles is _____. 1 2 4 3 5 6 8 7

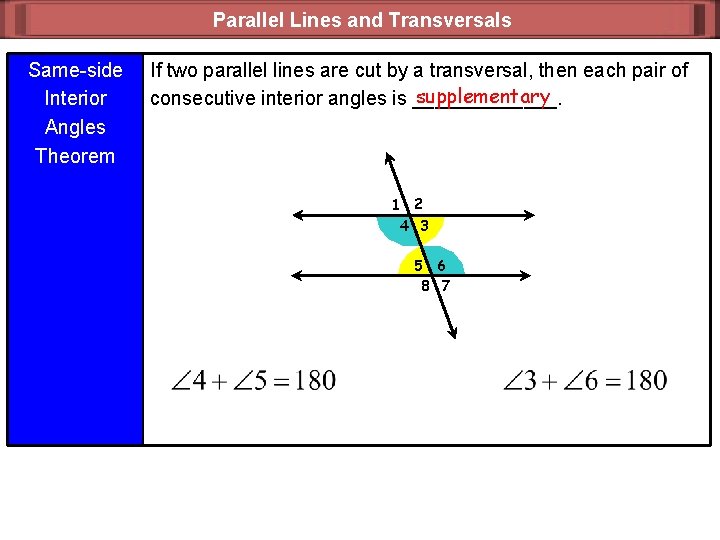
Parallel Lines and Transversals Same-side Interior Angles Theorem If two parallel lines are cut by a transversal, then each pair of supplementary consecutive interior angles is _______. 1 2 4 3 5 6 8 7

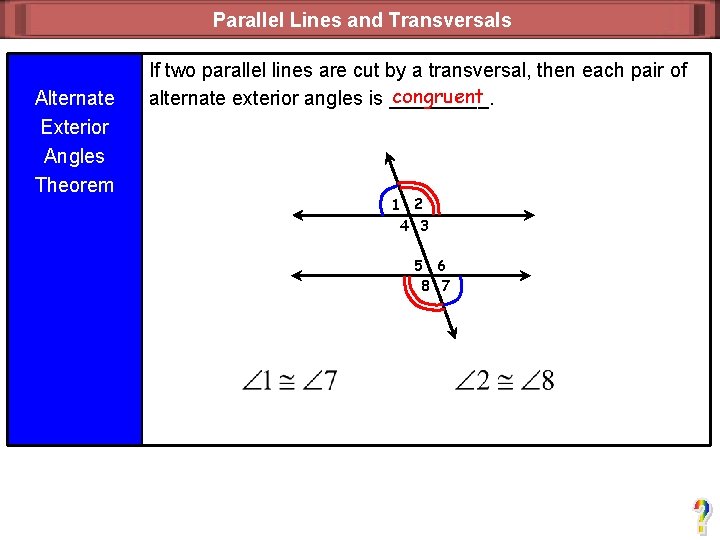
Parallel Lines and Transversals Alternate Exterior Angles Theorem If two parallel lines are cut by a transversal, then each pair of congruent alternate exterior angles is _____. 1 2 4 3 5 6 8 7

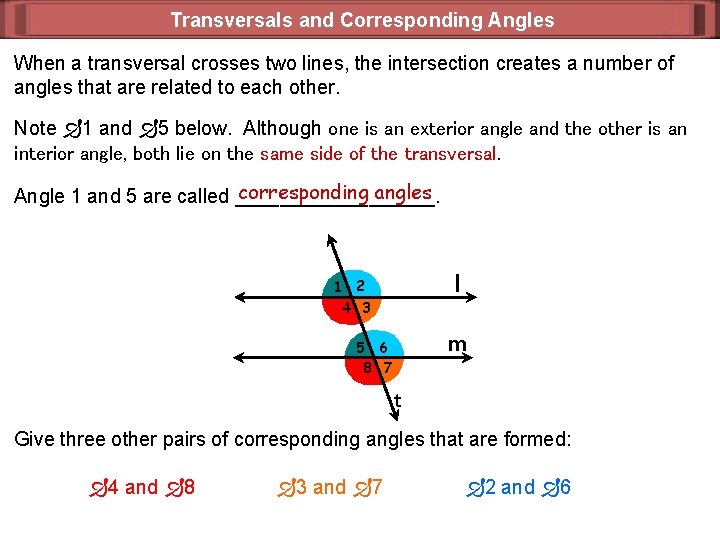
Transversals and Corresponding Angles When a transversal crosses two lines, the intersection creates a number of angles that are related to each other. Note 1 and 5 below. Although one is an exterior angle and the other is an interior angle, both lie on the same side of the transversal. corresponding angles Angle 1 and 5 are called _________. l 1 2 4 3 m 5 6 8 7 t Give three other pairs of corresponding angles that are formed: 4 and 8 3 and 7 2 and 6

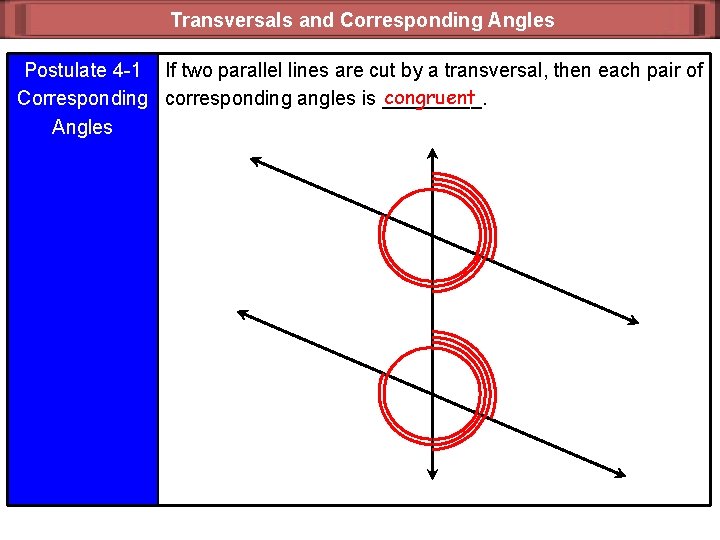
Transversals and Corresponding Angles Postulate 4 -1 If two parallel lines are cut by a transversal, then each pair of congruent Corresponding corresponding angles is _____. Angles

Transversals and Corresponding Angles Types of angle pairs formed when a transversal cuts two parallel lines. Concept Summary Congruent Supplementary alternate interior consecutive interior alternate exterior corresponding

Transversals and Corresponding Angles s s || t and c || d. Name all the angles that are congruent to 1. Give a reason for each answer. 1 2 5 6 9 10 13 14 3 1 corresponding angles 6 1 vertical angles 8 1 alternate exterior angles 9 1 corresponding angles 14 1 alternate exterior angles 11 9 1 corresponding angles 16 14 1 corresponding angles t 3 7 11 12 15 16 c 4 8 d

Proving Lines Parallel You will learn to identify conditions that produce parallel lines. Reminder: In Chapter 1, we discussed “if-then” statements (pg. 24). hypothesis and the Within those statements, we identified the “_____” conclusion “_____”. I said then that in mathematics, we only use the term “if and only if” if the converse of the statement is true.

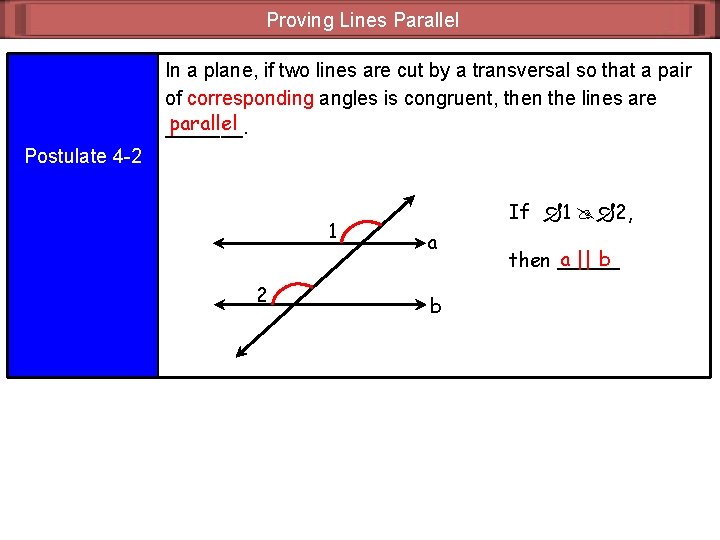
Proving Lines Parallel Postulate 4 – 1 (pg. 156): two parallel lines are cut by a transversal IF __________________, each pair of corresponding angles is congruent THEN ____________________. The postulates used in § 4 - 4 are the converse of postulates that you already know. COOL, HUH? § 4 – 4, Postulate 4 – 2 (pg. 162): IF ____________________, THEN __________________.

Proving Lines Parallel In a plane, if two lines are cut by a transversal so that a pair of corresponding angles is congruent, then the lines are parallel _______. Postulate 4 -2 1 2 If 1 2, a b a || b then _____

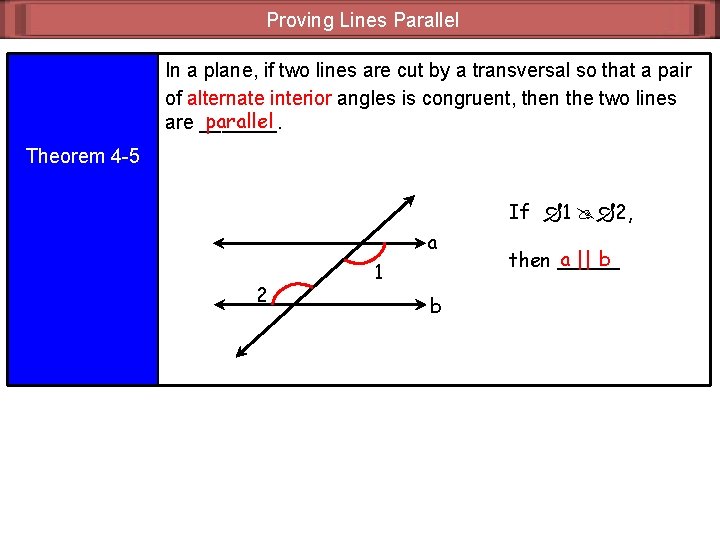
Proving Lines Parallel In a plane, if two lines are cut by a transversal so that a pair of alternate interior angles is congruent, then the two lines parallel are _______. Theorem 4 -5 If 1 2, a 2 1 b a || b then _____

Proving Lines Parallel In a plane, if two lines are cut by a transversal so that a pair of alternate exterior angles is congruent, then the two lines parallel are _______. Theorem 4 -6 1 2 If 1 2, a b a || b then _____

Proving Lines Parallel In a plane, if two lines are cut by a transversal so that a pair of consecutive interior angles is supplementary, then the two parallel lines are _______. Theorem 4 -7 If 1 + 2 = 180, 1 2 a b a || b then _____

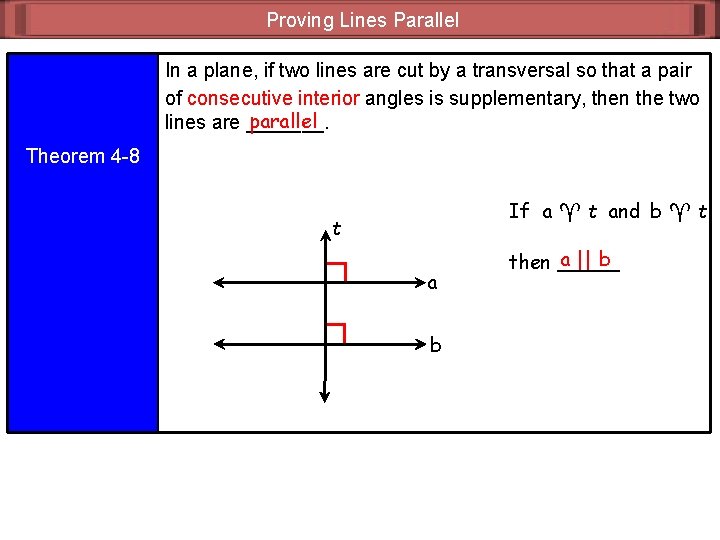
Proving Lines Parallel In a plane, if two lines are cut by a transversal so that a pair of consecutive interior angles is supplementary, then the two parallel lines are _______. Theorem 4 -8 If a t and b t, t a b a || b then _____

Proving Lines Parallel We now have five ways to prove that two lines are parallel. ØShow that a pair of corresponding angles is congruent. ØShow that a pair of alternate interior angles is congruent. Concept Summary ØShow that a pair of alternate exterior angles is congruent. ØShow that a pair of consecutive interior angles is supplementary. ØShow that two lines in a plane are perpendicular to a third line.

Proving Lines Parallel Identify any parallel segments. Explain your reasoning. G R A Y 90° D

Proving Lines Parallel Find the value for x so BE || TS. B T (6 x - 26)° (2 x + 10)° (5 x + 2)° ES is a transversal for BE =and TS. m BES + m EST 180 (2 x + and 10) + EST (5 x +are 2)consecutive = 180 interior angles. BES _________ 7 x + 12 = 180 If m BES + m EST = 180, then BE || TS by Theorem 4 – 7. 7 x = 168 x = 24 Thus, if x = 24, then BE || TS. S E

Slope You will learn to find the slopes of lines and use slope to identify parallel and perpendicular lines.

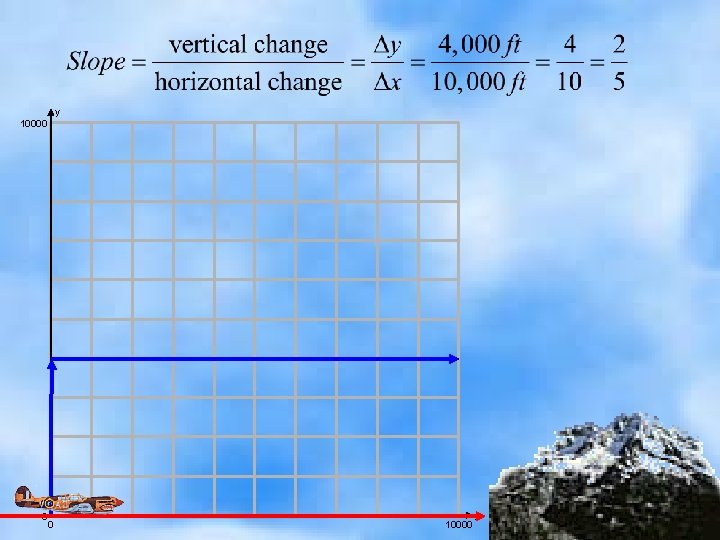
There has the got to bechange some “measurable” to will get not this make aircraft If the pilot doesn’t something, heway / she it Consider options: to clearfor such obstacles. home Christmas. Would you agree? 1) Keep the same slope of his / her path. Discuss you might radio a pilot and tell him or her how to Not ahow good choice! adjust the slope of their flight path in order to clear the mountain. 2) Go straight up. Not possible! This is an airplane, not a helicopter.

Fortunately, there is a way to measure a proper “slope” to clear the obstacle. We measure the “change in height” required and divide that by the “horizontal change” required.

y 10000 0 0 10000 x

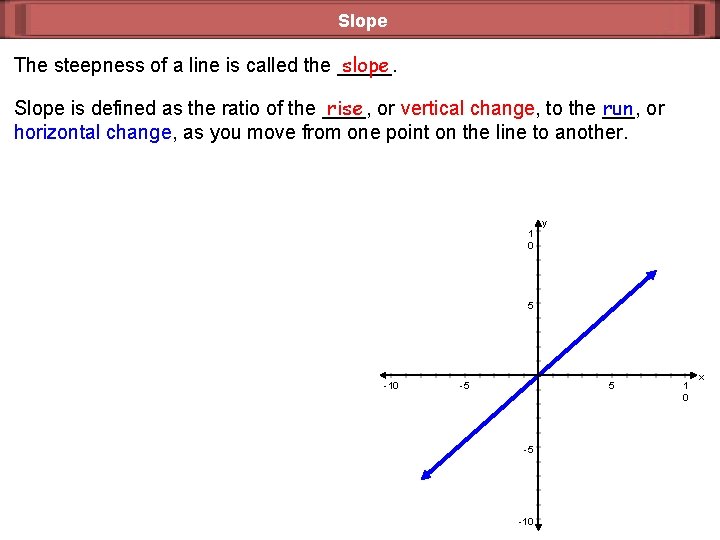
Slope slope The steepness of a line is called the _____. Slope is defined as the ratio of the ____, run or rise or vertical change, to the ___, horizontal change, as you move from one point on the line to another. 1 0 y 5 -10 -5 5 -5 -10 1 0 x

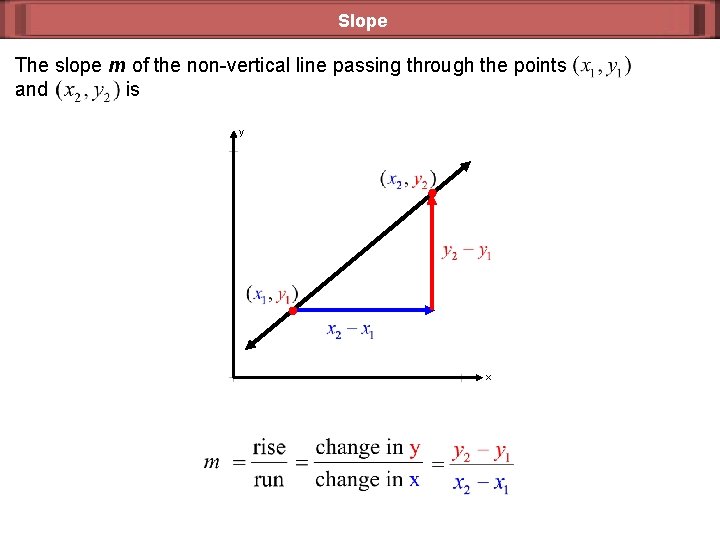
Slope The slope m of the non-vertical line passing through the points and is y x

Slope The slope “m” of a line containing two points with coordinates (x 1, y 1), and (x 2, y 2), is given by the formula Definition of Slope

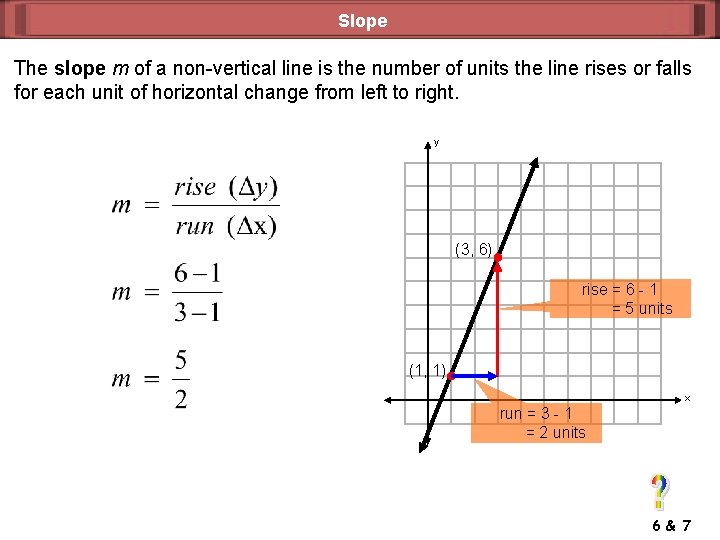
Slope The slope m of a non-vertical line is the number of units the line rises or falls for each unit of horizontal change from left to right. y (3, 6) rise = 6 - 1 = 5 units (1, 1) x run = 3 - 1 = 2 units 6 & 7

Slope Two distinct nonvertical lines are parallel iff they have the same slope _______. Postulate 4– 3

Slope Two nonvertical lines are perpendicular iff the product of their slope is -1 ______________. Postulate 4– 4 8 & 9

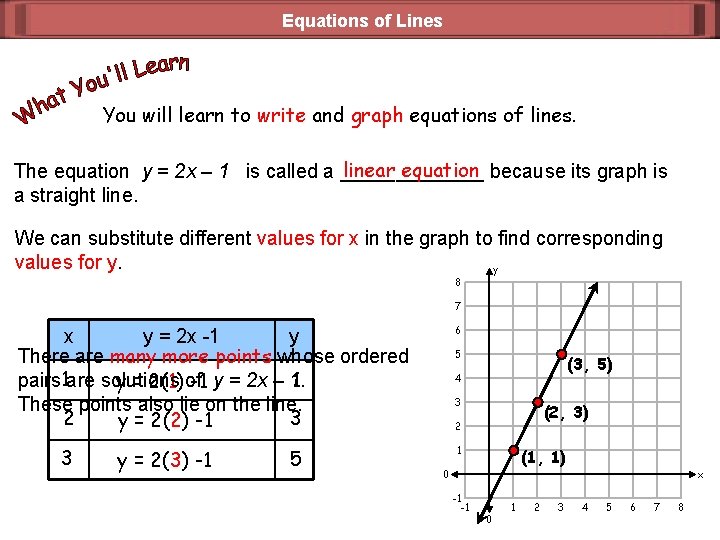
Equations of Lines You will learn to write and graph equations of lines. linear equation because its graph is The equation y = 2 x – 1 is called a _______ a straight line. We can substitute different values for x in the graph to find corresponding values for y. y 8 7 6 x y = 2 x -1 y There are many more points whose ordered 1 pairs 1 are solutions y = 2(1) of -1 y = 2 x – 1. These points also lie on the line. 2 3 y = 2(2) -1 3 y = 2(3) -1 5 5 (3, 5) 4 3 (2, 3) 2 1 (1, 1) 0 -1 -1 0 1 2 3 x 4 5 6 7 8

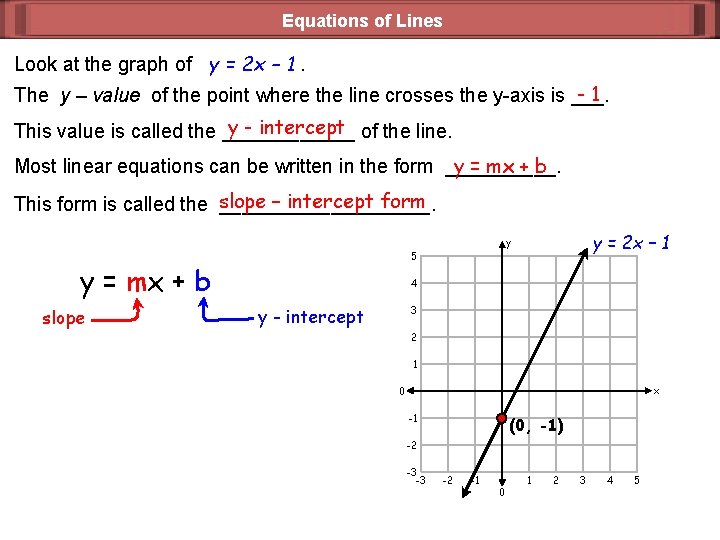
Equations of Lines Look at the graph of y = 2 x – 1. -1 The y – value of the point where the line crosses the y-axis is ___. y - intercept of the line. This value is called the ______ y = mx + b Most linear equations can be written in the form _____. – intercept form This form is called the slope __________. y = mx + b slope y = 2 x – 1 y 5 4 3 y - intercept 2 1 x 0 -1 (0, -1) -2 -3 -3 -2 -1 0 1 2 3 4 5

Equations of Lines Slope – Intercept Form An equation of the line having slope m and y-intercept b is y = mx + b

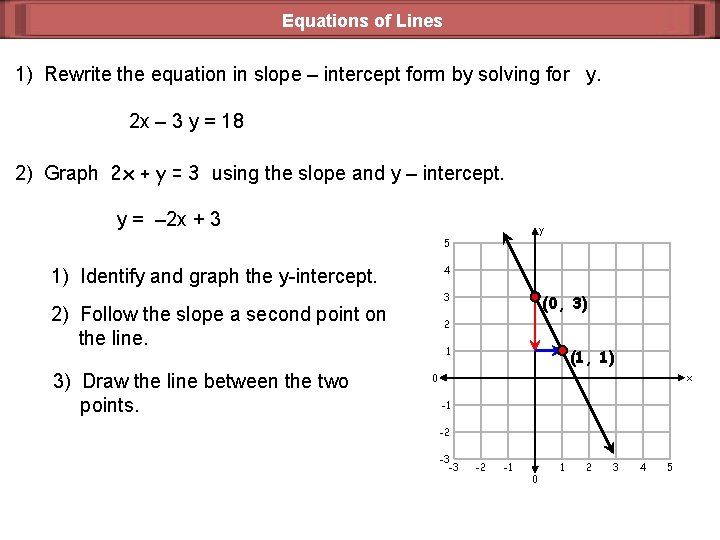
Equations of Lines 1) Rewrite the equation in slope – intercept form by solving for y. 2 x – 3 y = 18 2) Graph 2 x + y = 3 using the slope and y – intercept. y = – 2 x + 3 y 5 4 1) Identify and graph the y-intercept. 3 2) Follow the slope a second point on the line. 3) Draw the line between the two points. (0, 3) 2 1 (1, 1) x 0 -1 -2 -3 -3 -2 -1 0 1 2 3 4 5

Equations of Lines 1) Write an equation of the line parallel to the graph of y = 2 x – 5 that passes through the point (3, 7). y = 2 x + 1 2) Write an equation of the line parallel to the graph of 3 x + y = 6 that passes through the point (1, 4). y = -3 x + 7 3) Write an equation of the line perpendicualr to the graph of that passes through the point ( - 3, 8). y = -4 x -4