Parallel Jacobi Algorithm Steven Dong Applied Mathematics Overview

Parallel Jacobi Algorithm Steven Dong Applied Mathematics

Overview q Parallel Jacobi Algorithm v Different data distribution schemes • Row-wise distribution • Column-wise distribution • Cyclic shifting • Global reduction v Domain decomposition for solving Laplacian equations q Related MPI functions for parallel Jacobi algorithm and your project.

Linear Equation Solvers q Direct solvers v Gauss elimination v LU decomposition q Iterative solvers v Basic iterative solvers • Jacobi • Gauss-Seidel • Successive over-relaxation v Krylov subspace methods • Generalized minimum residual (GMRES) • Conjugate gradient

Sequential Jacobi Algorithm D is diagonal matrix L is lower triangular matrix U is upper triangular matrix

Parallel Jacobi Algorithm: Ideas q Shared memory or distributed memory: v Shared-memory parallelization very straightforward v Consider distributed memory machine using MPI q Questions to answer in parallelization: v Identify concurrency v Data distribution (data locality) • How to distribute coefficient matrix among CPUs? • How to distribute vector of unknowns? • How to distribute RHS? v Communication: What data needs to be communicated? q Want to: v v Achieve data locality Minimize the number of communications Overlap communications with computations Load balance

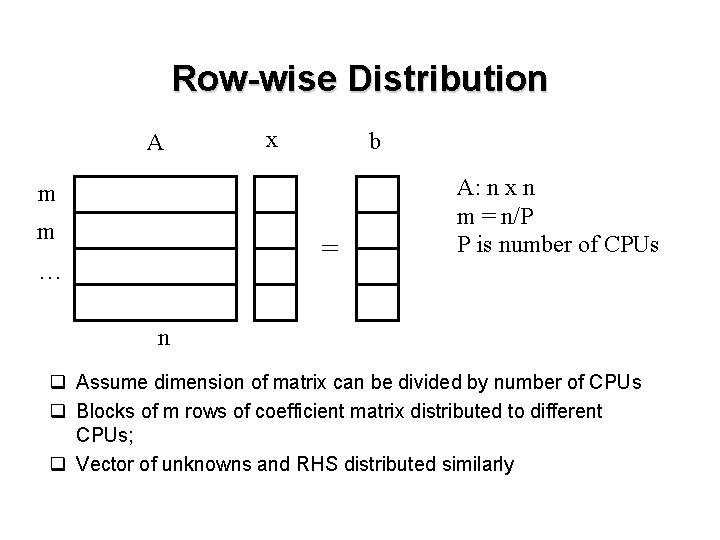
Row-wise Distribution A x b m m = … A: n x n m = n/P P is number of CPUs n q Assume dimension of matrix can be divided by number of CPUs q Blocks of m rows of coefficient matrix distributed to different CPUs; q Vector of unknowns and RHS distributed similarly

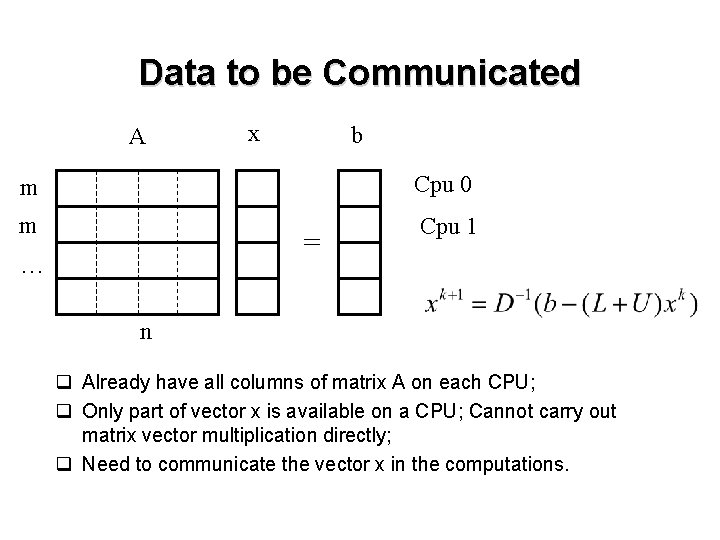
Data to be Communicated A x b m Cpu 0 m Cpu 1 = … n q Already have all columns of matrix A on each CPU; q Only part of vector x is available on a CPU; Cannot carry out matrix vector multiplication directly; q Need to communicate the vector x in the computations.

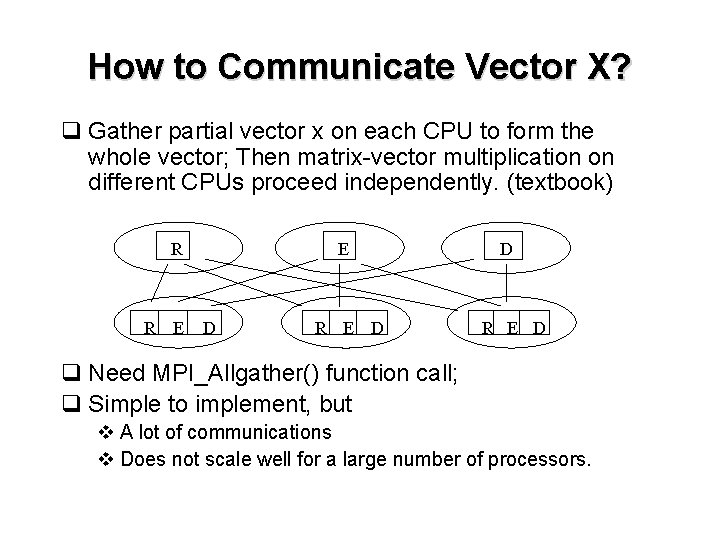
How to Communicate Vector X? q Gather partial vector x on each CPU to form the whole vector; Then matrix-vector multiplication on different CPUs proceed independently. (textbook) R R E E D R E D q Need MPI_Allgather() function call; q Simple to implement, but v A lot of communications v Does not scale well for a large number of processors.

How to Communicate X? q Another method: Cyclic shift v Shift partial vector x upward at each step; v Do partial matrix-vector multiplication on each CPU at each step; v After P steps (P is the number of CPUs), the overall matrixvector multiplication is complete. q Each CPU needs only to communicate with neighboring CPUs v Provides opportunities to overlap communication with computations q Detailed illustration …

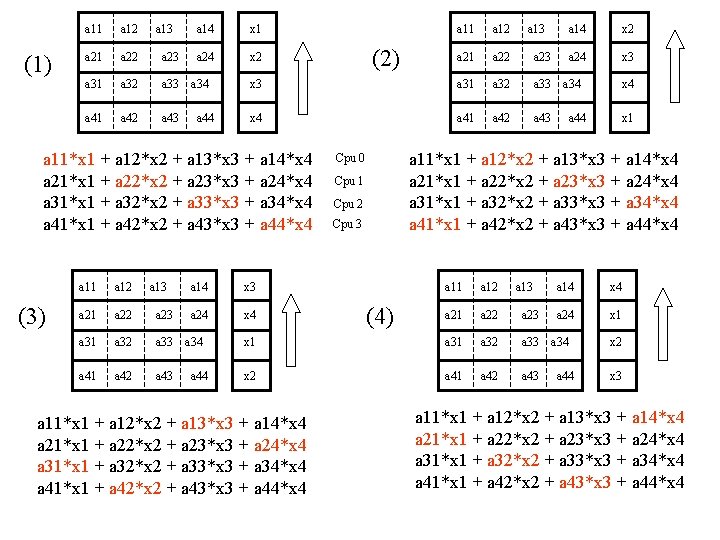
(1) a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 a 41 a 42 a 43 a 14 x 1 a 24 x 2 a 34 a 44 a 11 a 12 a 21 a 22 a 23 x 3 a 31 a 32 a 33 x 4 a 41 a 42 a 43 a 11*x 1 + a 12*x 2 + a 13*x 3 + a 14*x 4 a 21*x 1 + a 22*x 2 + a 23*x 3 + a 24*x 4 a 31*x 1 + a 32*x 2 + a 33*x 3 + a 34*x 4 a 41*x 1 + a 42*x 2 + a 43*x 3 + a 44*x 4 (3) a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 a 41 a 42 a 43 a 14 x 3 a 24 x 4 a 34 a 44 (2) a 13 x 2 a 24 x 3 a 34 x 4 a 44 x 1 a 11*x 1 + a 12*x 2 + a 13*x 3 + a 14*x 4 a 21*x 1 + a 22*x 2 + a 23*x 3 + a 24*x 4 a 31*x 1 + a 32*x 2 + a 33*x 3 + a 34*x 4 a 41*x 1 + a 42*x 2 + a 43*x 3 + a 44*x 4 Cpu 0 Cpu 1 Cpu 2 Cpu 3 a 11 a 12 a 21 a 22 a 23 x 1 a 32 a 33 x 2 a 41 a 42 a 43 a 11*x 1 + a 12*x 2 + a 13*x 3 + a 14*x 4 a 21*x 1 + a 22*x 2 + a 23*x 3 + a 24*x 4 a 31*x 1 + a 32*x 2 + a 33*x 3 + a 34*x 4 a 41*x 1 + a 42*x 2 + a 43*x 3 + a 44*x 4 a 14 (4) a 13 a 14 x 4 a 24 x 1 a 34 a 44 x 2 x 3 a 11*x 1 + a 12*x 2 + a 13*x 3 + a 14*x 4 a 21*x 1 + a 22*x 2 + a 23*x 3 + a 24*x 4 a 31*x 1 + a 32*x 2 + a 33*x 3 + a 34*x 4 a 41*x 1 + a 42*x 2 + a 43*x 3 + a 44*x 4

Overlap Communications with Computations q Communications: v Each CPU needs to send its own partial vector x to upper neighboring CPU; v Each CPU needs to receive data from lower neighboring CPU q Overlap communications with computations: Each CPU does the following: v Post non-blocking requests to send data to upper neighbor to to receive data from lower neighbor; This returns immediately v Do partial computation with data currently available; v Check non-blocking communication status; wait if necessary; v Repeat above steps

Stopping Criterion q Computing norm requires information of the whole vector; q Need a global reduction (SUM) to compute the norm using MPI_Allreduce or MPI_Reduce.

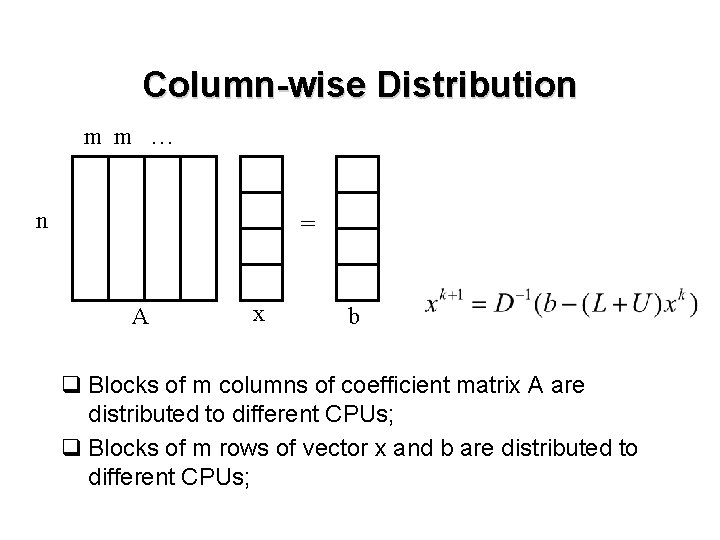
Column-wise Distribution m m … n = A x b q Blocks of m columns of coefficient matrix A are distributed to different CPUs; q Blocks of m rows of vector x and b are distributed to different CPUs;

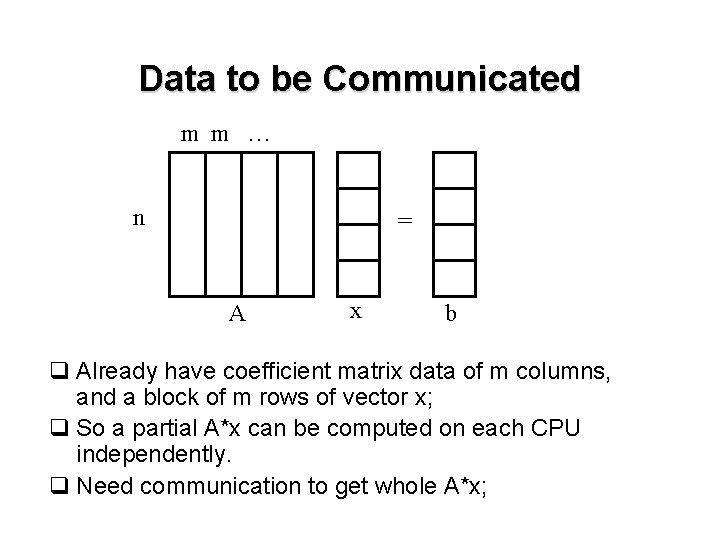
Data to be Communicated m m … n = A x b q Already have coefficient matrix data of m columns, and a block of m rows of vector x; q So a partial A*x can be computed on each CPU independently. q Need communication to get whole A*x;

How to Communicate q After getting partial A*x, can do global reduction (SUM) using MPI_Allreduce to get the whole A*x. So a new vector x can be calculated. q Another method: Cyclic shift v Shift coefficient matrix left-ward and vector of unknowns upward at each step; v Do a partial matrix-vector multiplication, and subtract it from the RHS; v After P steps (P is number of CPUs), matrix-vector multiplication is completed and subtracted from RHS; Can compute new vector x. q Detailed illustration …

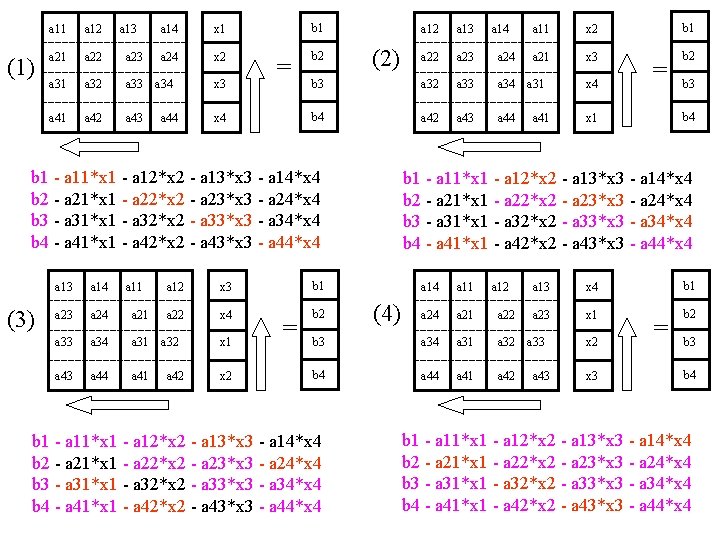
(1) a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 a 41 a 42 a 43 a 14 x 1 a 24 x 2 a 34 a 44 x 3 b 1 = x 4 a 12 a 13 a 22 a 23 a 24 b 3 a 32 a 33 a 34 b 4 a 42 a 43 a 44 b 2 (2) b 1 - a 11*x 1 - a 12*x 2 - a 13*x 3 - a 14*x 4 b 2 - a 21*x 1 - a 22*x 2 - a 23*x 3 - a 24*x 4 b 3 - a 31*x 1 - a 32*x 2 - a 33*x 3 - a 34*x 4 b 4 - a 41*x 1 - a 42*x 2 - a 43*x 3 - a 44*x 4 (3) a 13 a 14 a 11 a 23 a 24 a 21 a 33 a 34 a 31 a 43 a 44 a 41 a 12 x 3 b 1 a 22 x 4 b 2 a 32 a 42 x 1 x 2 = a 14 x 2 b 1 a 21 x 3 b 2 a 31 a 41 x 4 = b 3 b 4 x 1 b 1 - a 11*x 1 - a 12*x 2 - a 13*x 3 - a 14*x 4 b 2 - a 21*x 1 - a 22*x 2 - a 23*x 3 - a 24*x 4 b 3 - a 31*x 1 - a 32*x 2 - a 33*x 3 - a 34*x 4 b 4 - a 41*x 1 - a 42*x 2 - a 43*x 3 - a 44*x 4 a 11 a 24 a 21 a 22 b 3 a 34 a 31 a 32 b 4 a 41 a 42 b 1 - a 11*x 1 - a 12*x 2 - a 13*x 3 - a 14*x 4 b 2 - a 21*x 1 - a 22*x 2 - a 23*x 3 - a 24*x 4 b 3 - a 31*x 1 - a 32*x 2 - a 33*x 3 - a 34*x 4 b 4 - a 41*x 1 - a 42*x 2 - a 43*x 3 - a 44*x 4 a 11 (4) a 12 a 13 x 4 b 1 a 23 x 1 b 2 a 33 a 43 x 2 x 3 = b 3 b 4 b 1 - a 11*x 1 - a 12*x 2 - a 13*x 3 - a 14*x 4 b 2 - a 21*x 1 - a 22*x 2 - a 23*x 3 - a 24*x 4 b 3 - a 31*x 1 - a 32*x 2 - a 33*x 3 - a 34*x 4 b 4 - a 41*x 1 - a 42*x 2 - a 43*x 3 - a 44*x 4

Solving Diffusion Equation q How do we solve it in parallel in practice? q Need to do domain decomposition.

Domain Decomposition cpu 0 cpu 1 … q Column-wise decomposition q Boundary points depend on data from neighboring CPU v During each iteration, need send own boundary data to neighbors, and receive boundary data from neighboring CPUs. y x q Interior points depend only on data residing on the same CPU (local data).

Overlap Communication with Computations q Compute boundary points and interior points at different stages; q Specifically: v At the beginning of an iteration, post non-blocking send to and receive from requests for communicating boundary data with neighboring CPUs; v Update values on interior points; v Check communication status (should complete by this point), wait if necessary; v Boundary data received, update boundary points; v Begin next iteration, repeat above steps.

Other Domain Decompositions 1 D decomposition 2 D decomposition

Related MPI Functions for Parallel Jacobi Algorithm q MPI_Allgather() q MPI_Isend() q MPI_Irecv() q MPI_Reduce() q MPI_Allreduce()

MPI Programming Related to Your Project q Parallel Jacobi Algorithm q Compiling MPI programs q Running MPI programs q Machines: www. cascv. brown. edu