Parallel Graph Algorithms Oct 25 2012 copyright 2012

Parallel Graph Algorithms Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

Graph Algorithms • Minimum Spanning Tree (Prim’s Algorithm) • Single-Source Shortest Path (Dijkstra’s Algorithm) • All-Pairs Shortest Paths (Dijkstra’s and Floyd’s Algorithm) Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

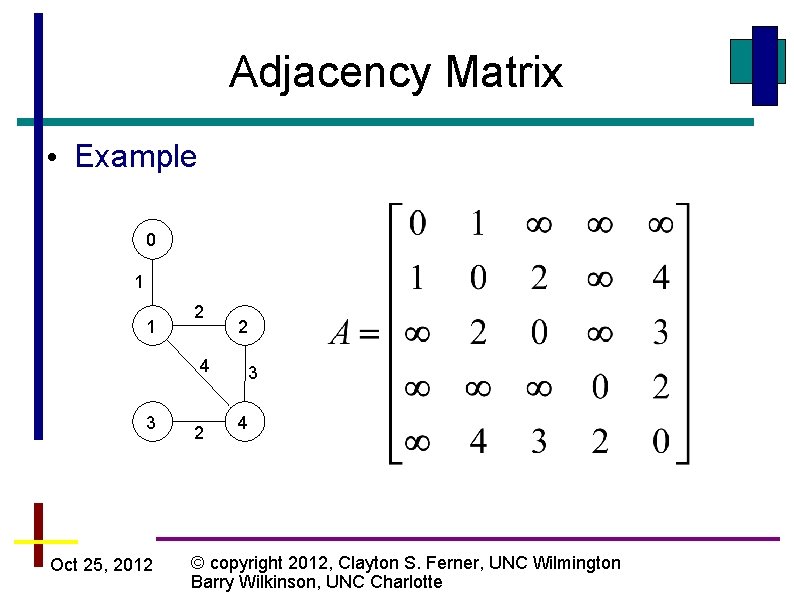
Adjacency Matrix • An adjacency matrix represent the edges of a graph Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

Adjacency Matrix • Example 0 1 1 2 4 3 Oct 25, 2012 2 2 3 4 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

Prim’s Algorithm for Minimum Spanning Tree Prim_MST(V, E, A, r) { VT = {r}; d[r] = 0; for all v in (V – VT) d[v] = Ar, v; V – set of vertices VT – set of vertices in the MST E – set of edges A – adjacency matrix r – root node d – minimum distance from MST to any vertex while (VT != V) { Find a vertex u such that d[u] = min(d[v] for all v in (V – VT)); VT = VT + {u}; for all v in (V – VT) { Complexity d[v] = min(d[v], Au, v); } } } Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte = O(n 2)

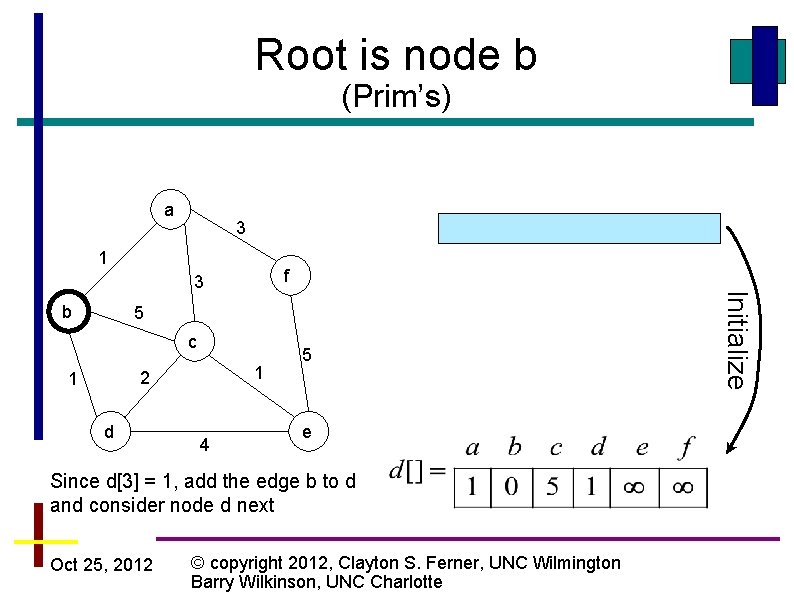
Root is node b (Prim’s) a 3 1 f b 5 c 1 2 1 d 4 5 e Since d[3] = 1, add the edge b to d and consider node d next Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte Initialize 3

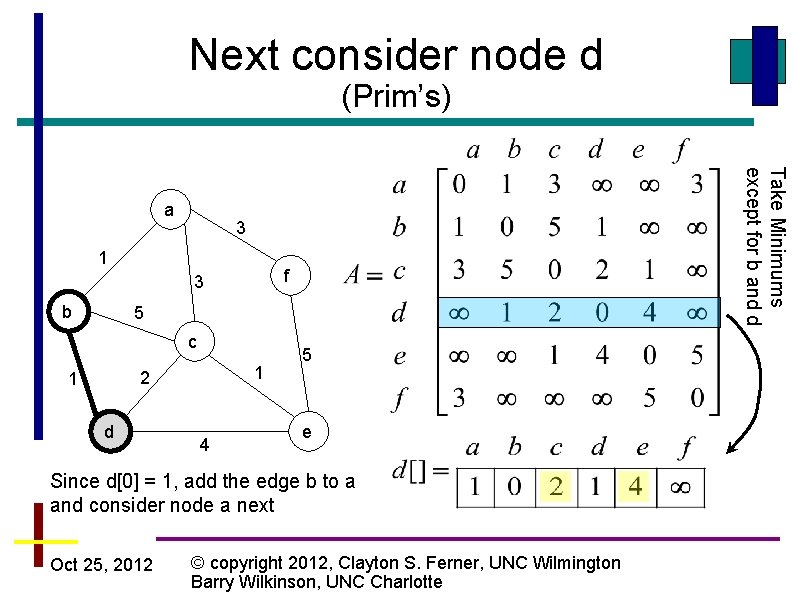
Next consider node d (Prim’s) 3 1 f 3 b Take Minimums except for b and d a 5 c 1 2 1 d 4 5 e Since d[0] = 1, add the edge b to a and consider node a next Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

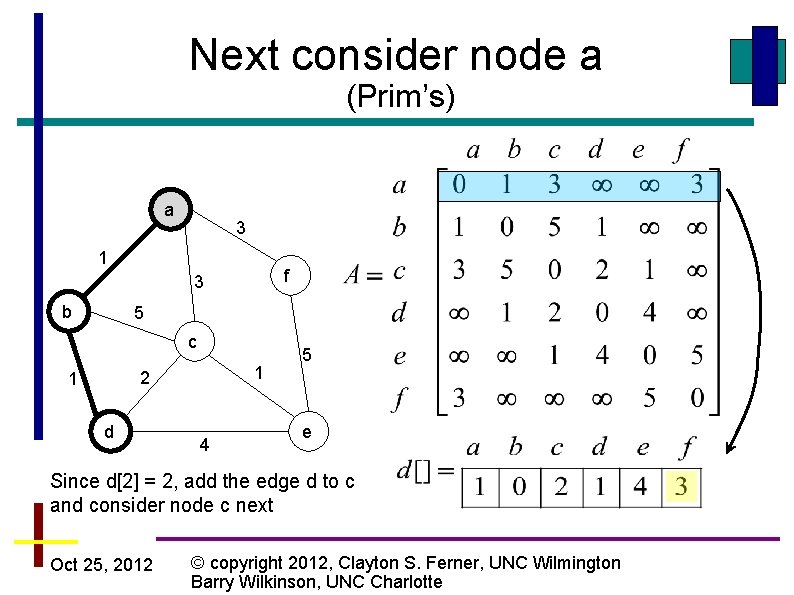
Next consider node a (Prim’s) a 3 1 f 3 b 5 c 1 2 1 d 4 5 e Since d[2] = 2, add the edge d to c and consider node c next Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

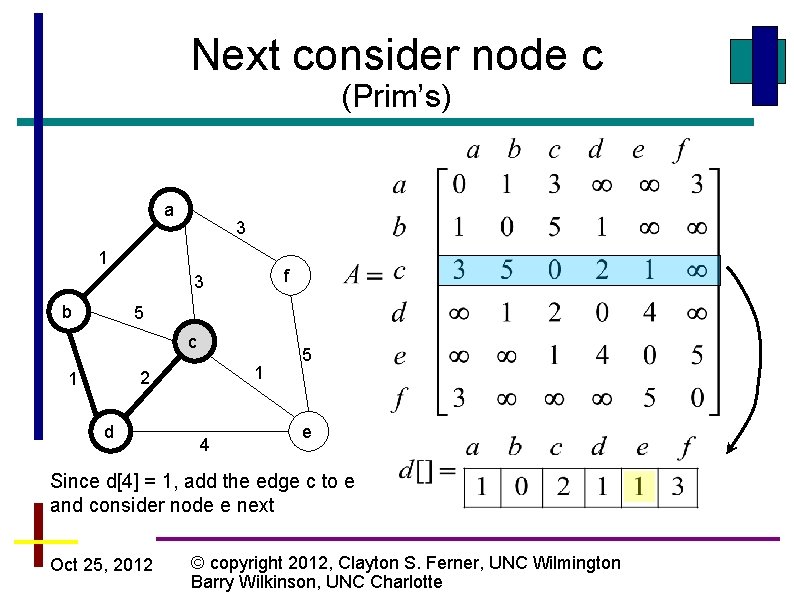
Next consider node c (Prim’s) a 3 1 f 3 b 5 c 1 2 1 d 4 5 e Since d[4] = 1, add the edge c to e and consider node e next Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

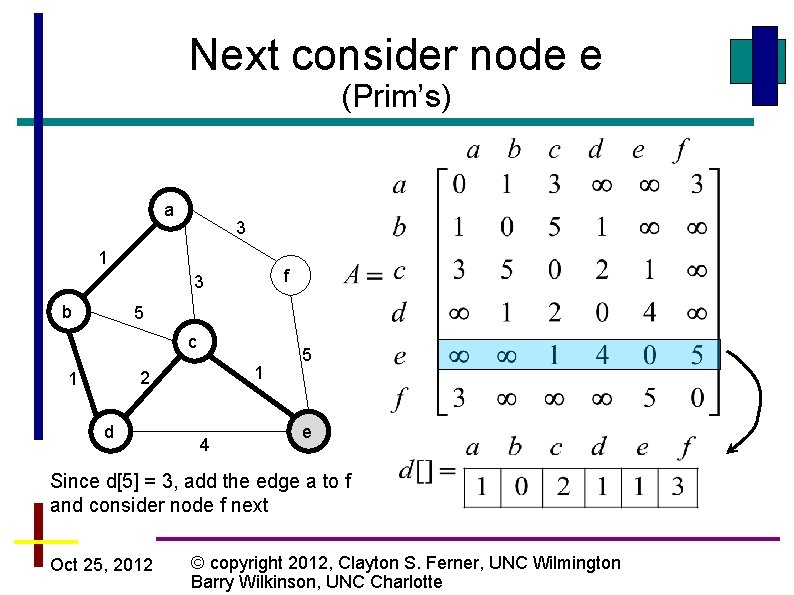
Next consider node e (Prim’s) a 3 1 f 3 b 5 c 1 2 1 d 4 5 e Since d[5] = 3, add the edge a to f and consider node f next Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

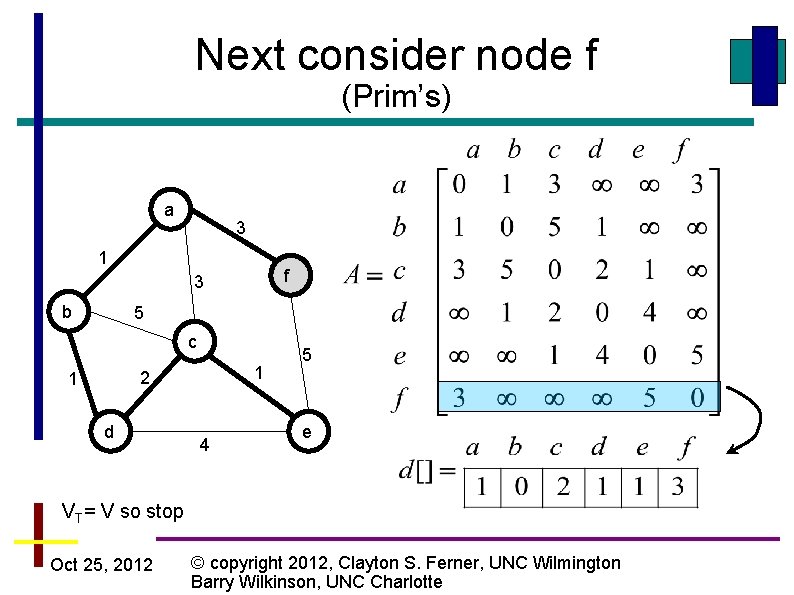
Next consider node f (Prim’s) a 3 1 f 3 b 5 c 1 2 1 d 4 5 e VT= V so stop Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

Parallelizing Prim’s Algorithm • We can’t just simply execute the while loop in parallel because the d[] array changes with each selection of a vertex • We have to update values in d[] from all processors after each iteration • Suppose we have n vertices in the graph and p processors Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

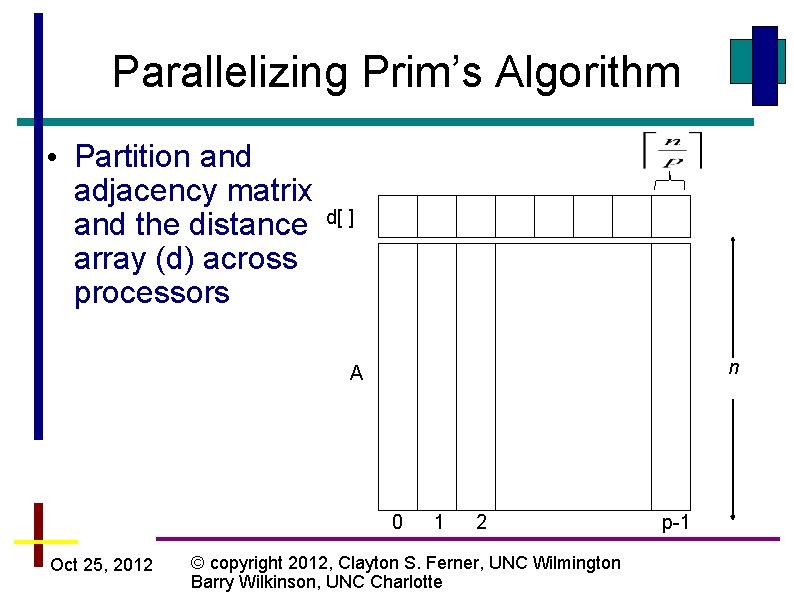
Parallelizing Prim’s Algorithm • Partition and adjacency matrix and the distance array (d) across processors d[ ] n A 0 Oct 25, 2012 1 2 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte p-1

Parallelizing Prim’s Algorithm • Each processor computes the next vertex from among its vertices • A reduction is done on the distance array (d) to find the minimum • The result is broadcast out to all the processors Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

Which pattern does this fit? Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

Prim’s Algorithm (Parallel) Prim_MST(V, E, A, r) {. . . // Initialize d as before #pragma paraguin begin_parallel while (VT != V) { Find a vertex u such that d[u] = min(d[v] for all v in (V – VT)); VT = VT + {u}; #pragma paraguin forall for v in V if (v VT) d[v] = min(d[v], Au, v); #pragma paraguin reduce min d #pragma paraguin bcast d } #pragma paraguin end_parallel } Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

Prim’s Algorithm (Parallel) • Complexity of Parallel algorithm: Communication Computation • Each reduction and broadcast takes log p time, but we have to do up to n of them. Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

Dijkstra’s Algorithm for Single. Source Shortest Path • Given a source node, what is the shortest distance to each other node • The minimum spanning tree gives is this information Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

Dijkstra’s Algorithm Dijkstra_SP(V, E, A, r) { VT = {r}; d[r] = 0; for v in (V – VT) d[v] = Ar, v; V – set of vertices VT – set of vertices in the MST E – set of edges A – adjacency matrix r – root node d – minimum distance from root to any vertex while (VT != V) { Find a vertex v such that d[u] = min(d[v] for all v in (V – VT)); VT = VT + {u}; for v in (V – VT) Complexity d[v] = min(d[v], d[u] + Au, v); } } Oct 25, 2012 This is the only thing different © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte = O(n 2)

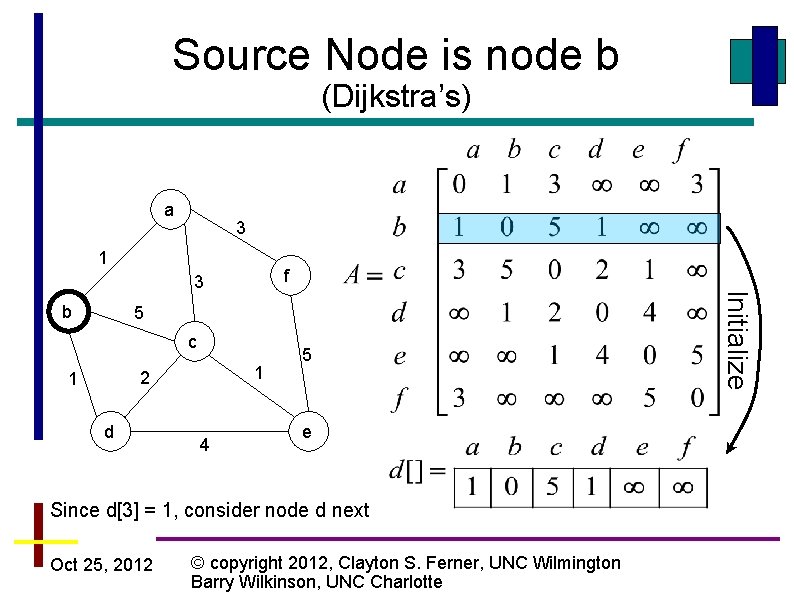
Source Node is node b (Dijkstra’s) a 3 1 f b 5 c 1 2 1 d 4 5 e Since d[3] = 1, consider node d next Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte Initialize 3

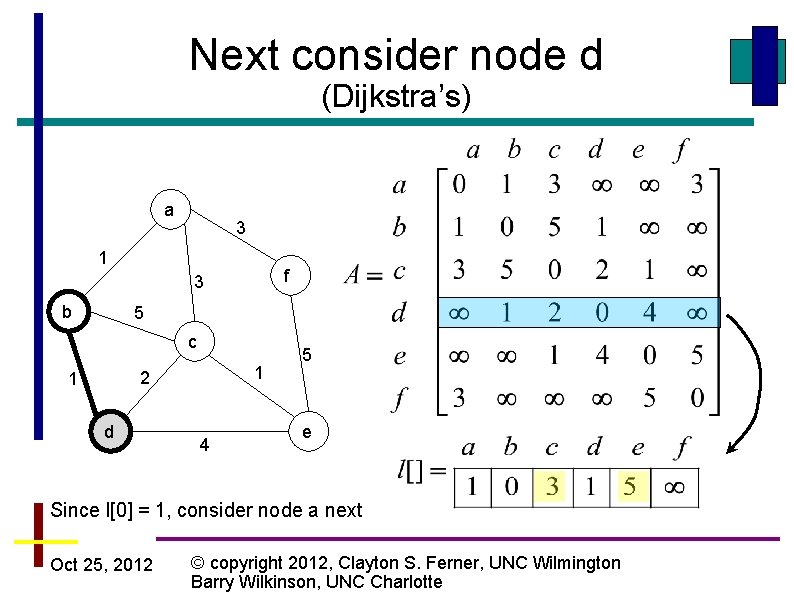
Next consider node d (Dijkstra’s) a 3 1 f 3 b 5 c 1 2 1 d 4 5 e Since l[0] = 1, consider node a next Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

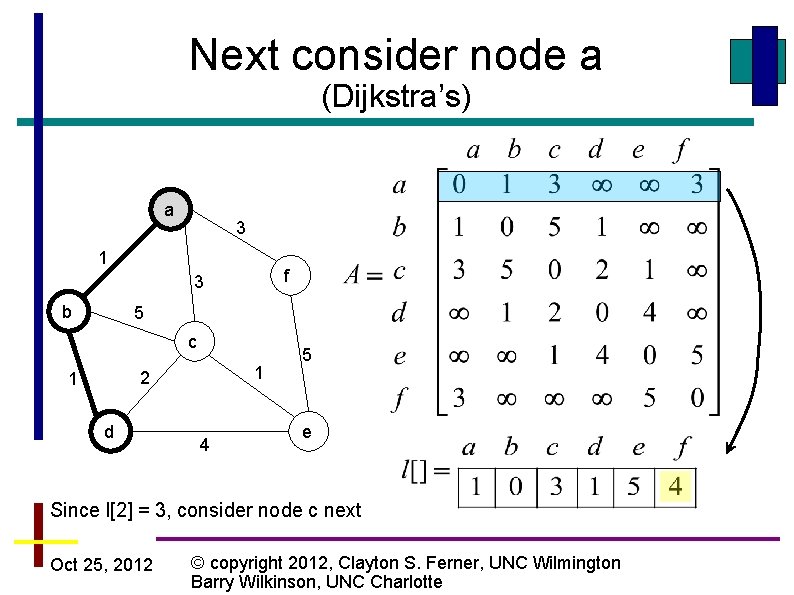
Next consider node a (Dijkstra’s) a 3 1 f 3 b 5 c 1 2 1 d 4 5 e Since l[2] = 3, consider node c next Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

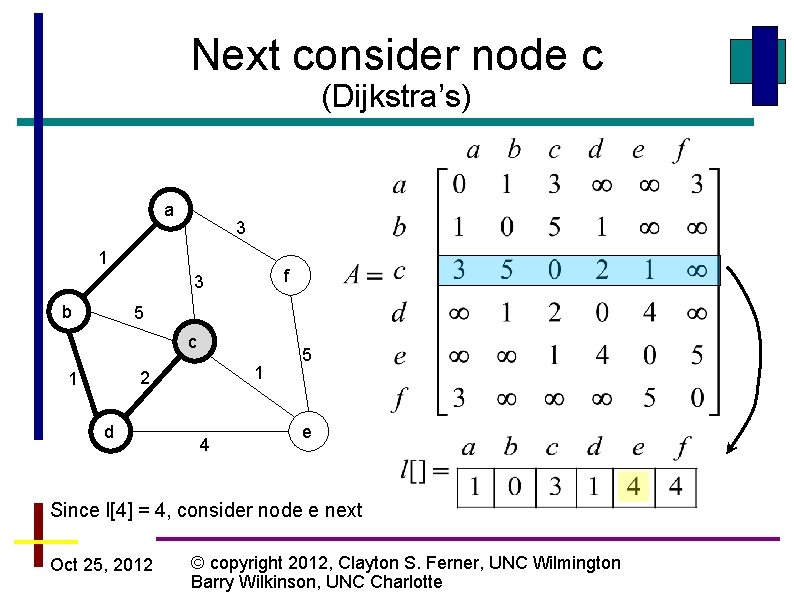
Next consider node c (Dijkstra’s) a 3 1 f 3 b 5 c 1 2 1 d 4 5 e Since l[4] = 4, consider node e next Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

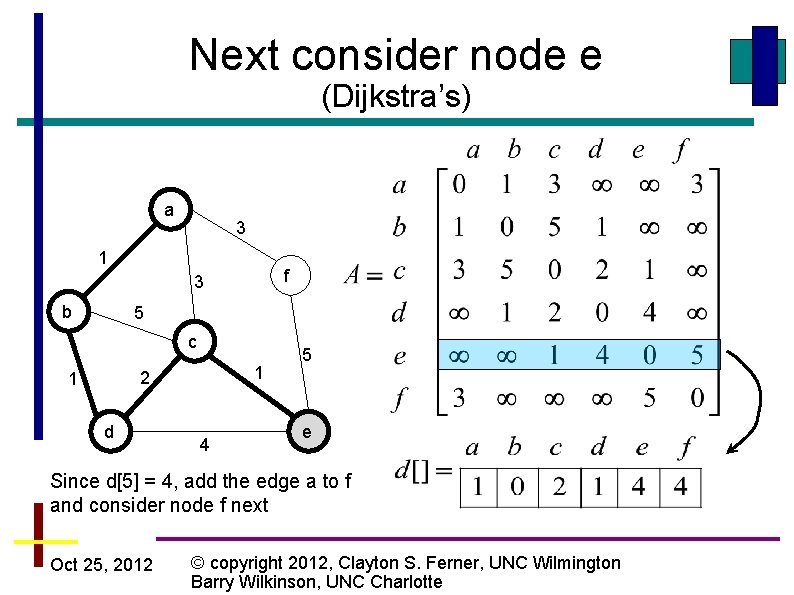
Next consider node e (Dijkstra’s) a 3 1 f 3 b 5 c 1 2 1 d 4 5 e Since d[5] = 4, add the edge a to f and consider node f next Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

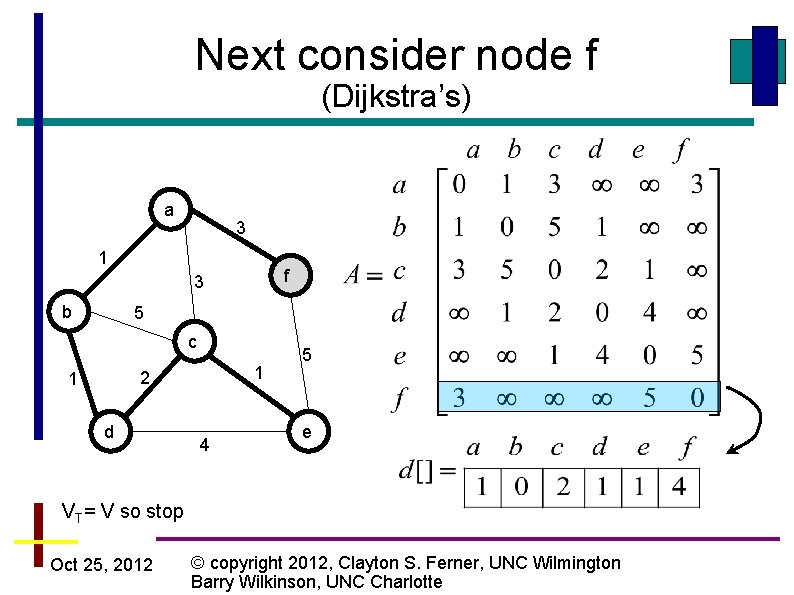
Next consider node f (Dijkstra’s) a 3 1 f 3 b 5 c 1 2 1 d 4 5 e VT= V so stop Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

Parallelizing Dijkstra’s Algorithm • Since Dijkstra’s Algorithm and Prim’s Algorithm are essentially the same, we can parallelize them the same way: • Complexity of Parallel algorithm: Communication Computation • If we have n processors, this becomes: Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

All Pairs Shortest Path • Dijkstra’s Algorithm gives us the shortest path from a particular node to all the others • For All Paris Shortest Path, we want to find the shortest path between all pairs of vertices • We can apply Dijkstra’s Algorithm to every pair of vertices • Complexity = O(n 3) Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

All Pairs using Dijkstra’s Algorithm Dijkstra_APSP(V, E, A) V – set of vertices { VT – set of vertices in the MST for r in V { E – set of edges VT = {r}; A – adjacency matrix d[N] = {0, … }; r – root node for all v in (V – VT) d – minimum distance from root to d[r][v] = Ar, v; any vertex while (VT != V) { Find a vertex u such that d[r][u] = min(d[r][v] for all v in (V – VT)); VT = VT + {u}; for v in (V – VT) d[r][v] = min(d[v], d[u] + Au, v); } } Complexity = O(n 3) } Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

All Pairs Shortest Path • We can parallelize the outermost loop • Each processors assumes a different node vi and computes the shortest path to all nodes • No communication if needed • Complexity is O(n 3/p) • If we have n processors, complexity is O(n 2) • If we have n 2 processors, we can use n processors for each vertex. Complexity becomes O(nlogn) Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

Floyd’s Algorithm for All Pairs Shortest Path • Floyd’s Algorithm works off of this observation: – Consider a subset of V: – Let be the weight of the shortest path from vi to vj that includes one of the vertices in – If vk is not in the shortest path from vi to vj, then – Otherwise, the shortest path is Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

Floyd’s Algorithm for All Pairs Shortest Path • This leads to the following recurrence: • We can implement this using iteration and not recursion Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

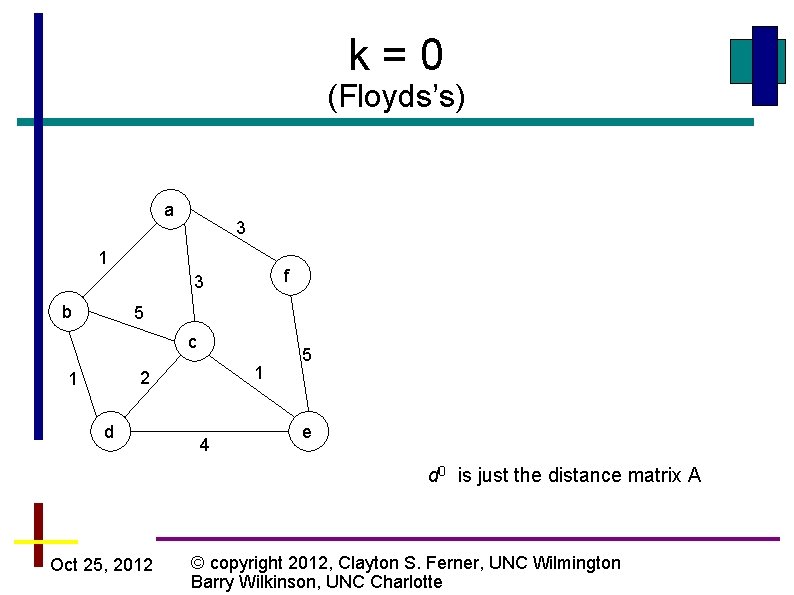
k=0 (Floyds’s) a 3 1 f 3 b 5 c 1 2 1 d 4 5 e d 0 is just the distance matrix A Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

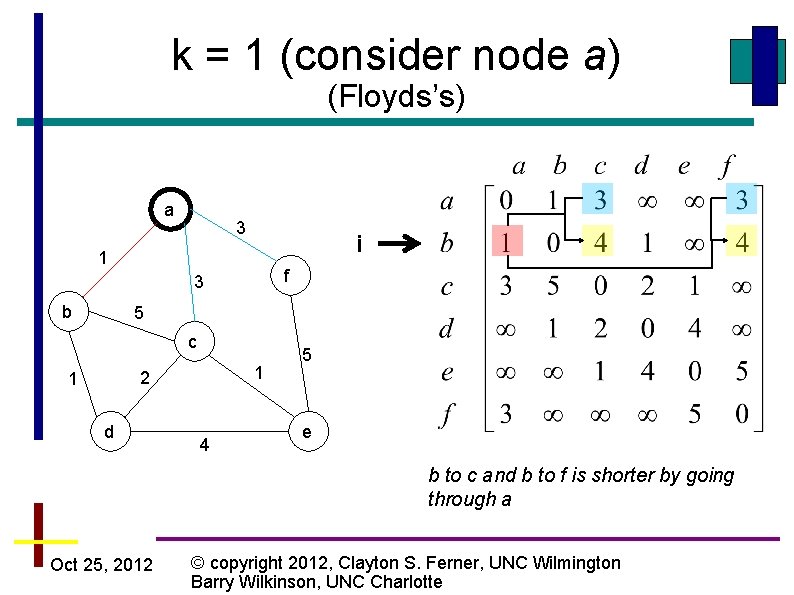
k = 1 (consider node a) (Floyds’s) a 3 i 1 f 3 b 5 c 1 2 1 d 4 5 e b to c and b to f is shorter by going through a Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

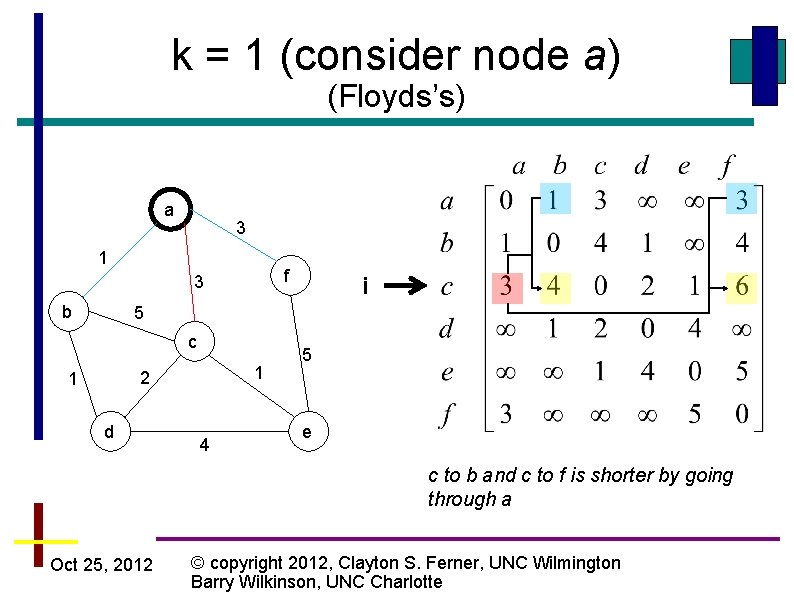
k = 1 (consider node a) (Floyds’s) a 3 1 f 3 b i 5 c 1 2 1 d 4 5 e c to b and c to f is shorter by going through a Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

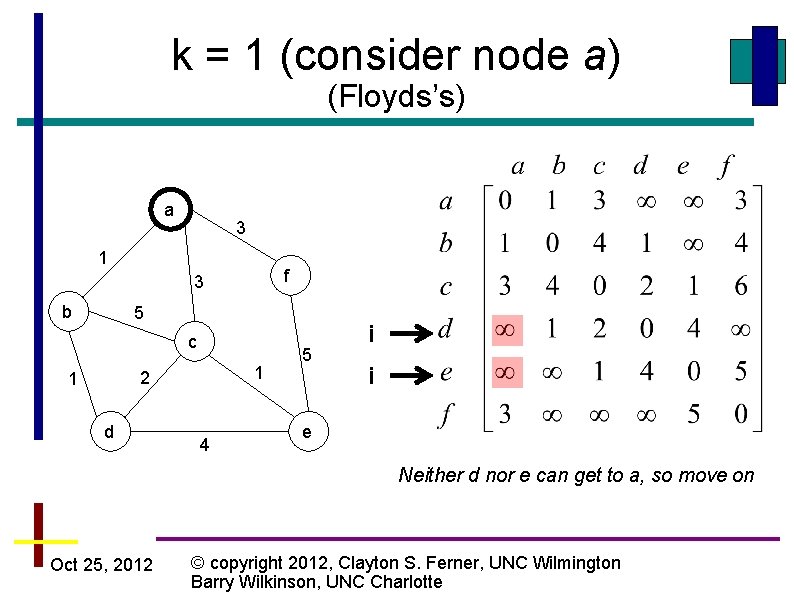
k = 1 (consider node a) (Floyds’s) a 3 1 f 3 b 5 c 1 2 1 d 4 5 i i e Neither d nor e can get to a, so move on Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

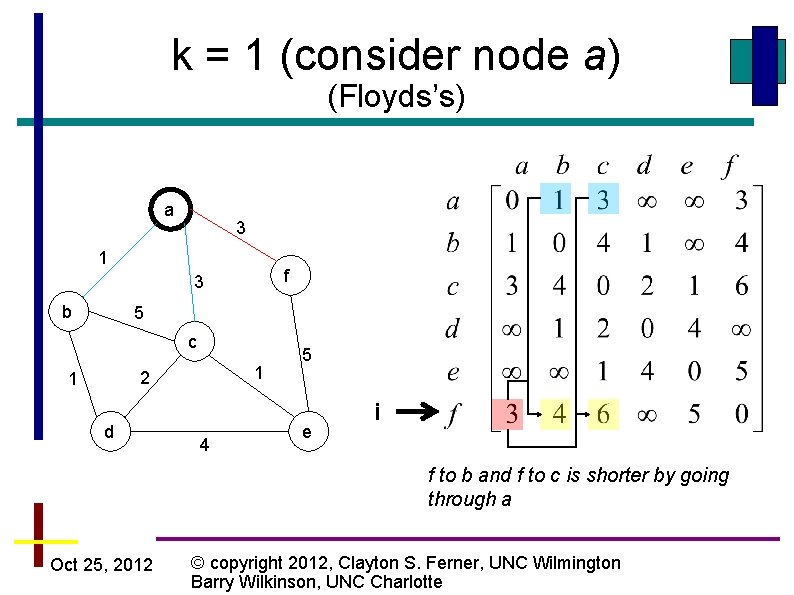
k = 1 (consider node a) (Floyds’s) a 3 1 f 3 b 5 c 1 2 1 d 4 5 e i f to b and f to c is shorter by going through a Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

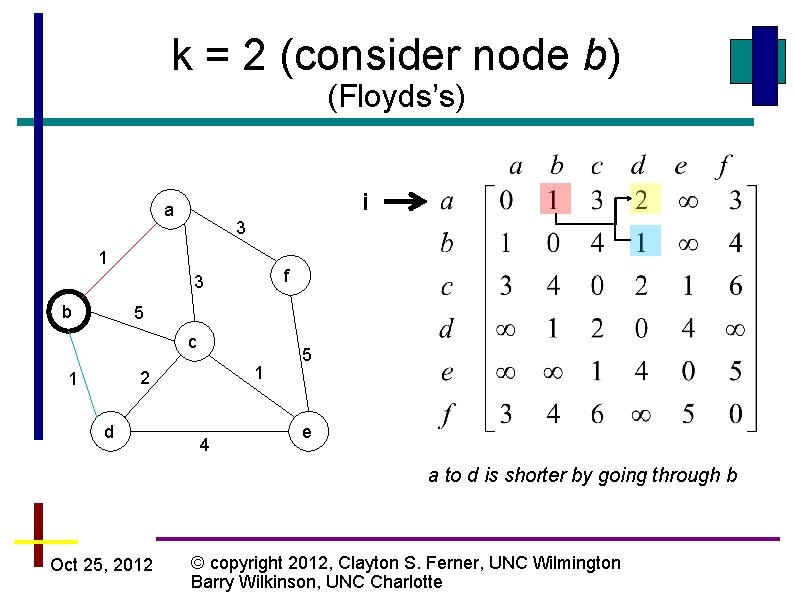
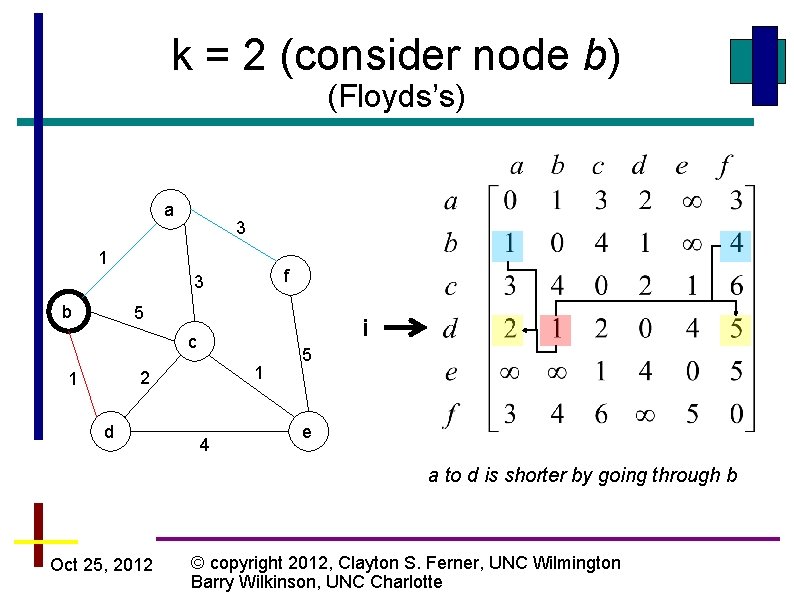
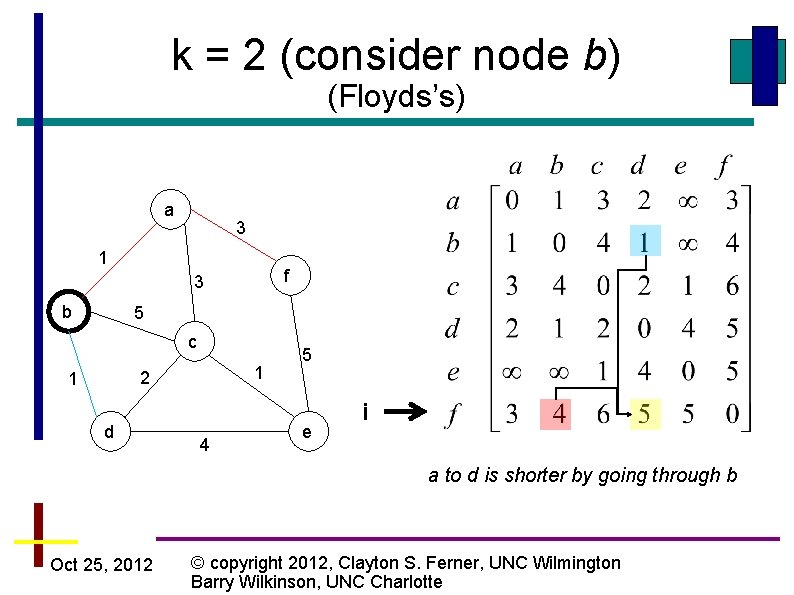
k = 2 (consider node b) (Floyds’s) i a 3 1 f 3 b 5 c 1 2 1 d 4 5 e a to d is shorter by going through b Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

k = 2 (consider node b) (Floyds’s) a 3 1 f 3 b 5 i c 1 2 1 d 4 5 e a to d is shorter by going through b Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

k = 2 (consider node b) (Floyds’s) a 3 1 f 3 b 5 c 1 2 1 d 4 5 e i a to d is shorter by going through b Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

All Pairs using Floyd’s Algorithm Floyd_APSP(V, E, A) { d 0 i, j = Ai, j for all i, j for k = 1 to n for i = 1 to n for j = 1 to n d(k)i, j = min(d(k-1)i, j V – set of vertices E – set of edges A – adjacency matrix , d(k-1)i, k + d(k-1)k, j ) Complexity = O(n 3) • We don’t need n copies of the d matrix. We only need one. • In fact, we can do it with only one matrix Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

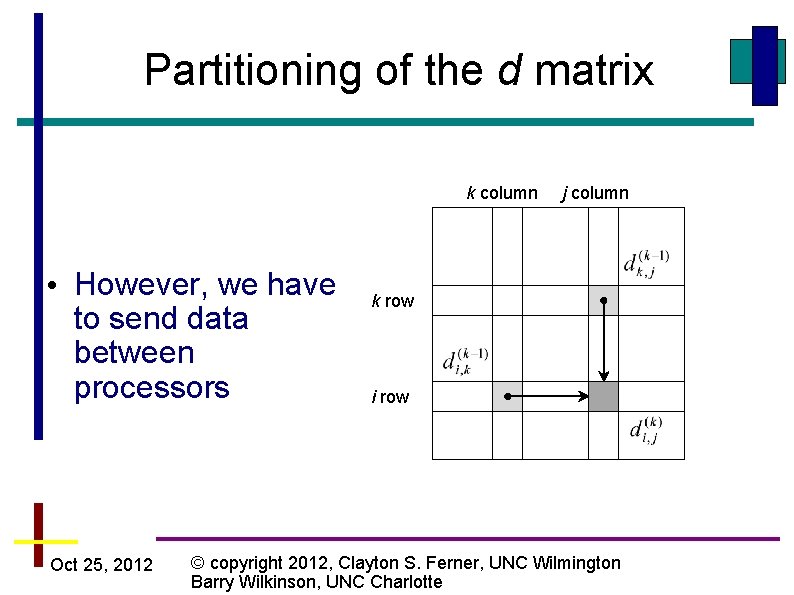
Partitioning of the d matrix Oct 25, 2012 … • We divide the d matrix into p blocks of size n/√p • Each processor is responsible for n 2/√p elements of the d matrix … … … © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

Partitioning of the d matrix k column • However, we have to send data between processors Oct 25, 2012 j column k row i row © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

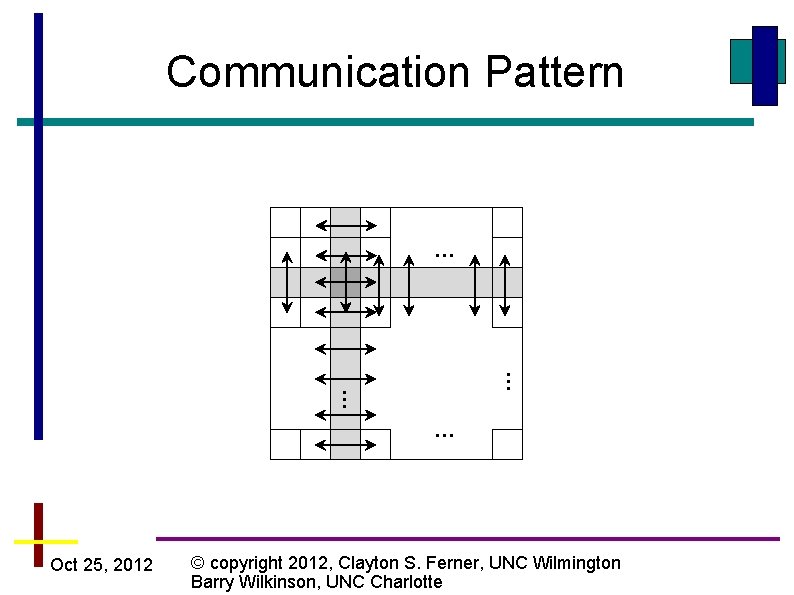
Which pattern does this fit? Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

Communication Pattern … … Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

Analysis of Floyd’s Algorithm • Each processor has to send its block to all processors on the same row and column. • If we use a broadcast, then the time for communication is • The synchronization step requires • The time to compute the new values for each step is Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

Analysis of Floyd’s Algorithm • So the complexity for each step is: • And finally, the complexity for n steps (of the k loop) is: Communication Computation Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

A faster version of Floyd’s Algorithm • We can do a pipeline of values moving through the matrix. • The reason is because once processor pi, j computes the value of it can then send it to the processors pi, j-1 , pi, j+1 , pi+1, j , and pi-1, j Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

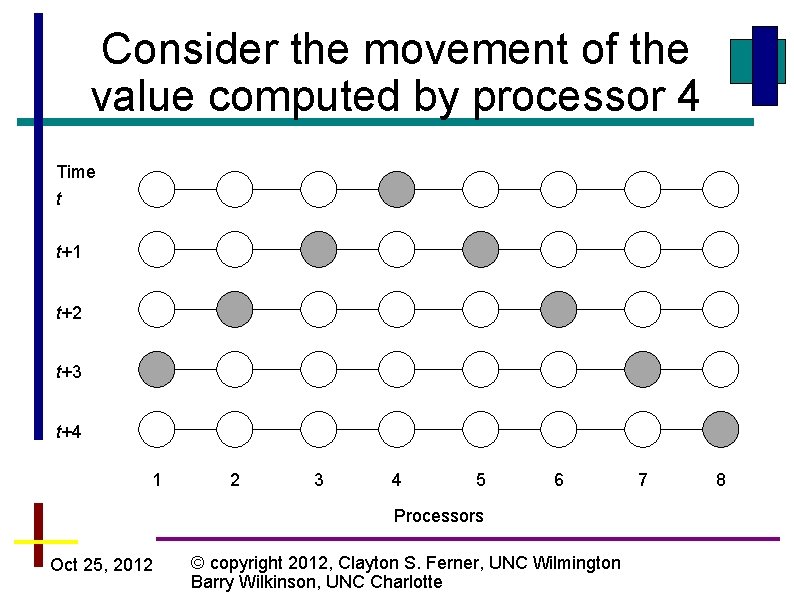
Consider the movement of the value computed by processor 4 Time t t+1 t+2 t+3 t+4 1 2 3 4 5 6 Processors Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte 7 8

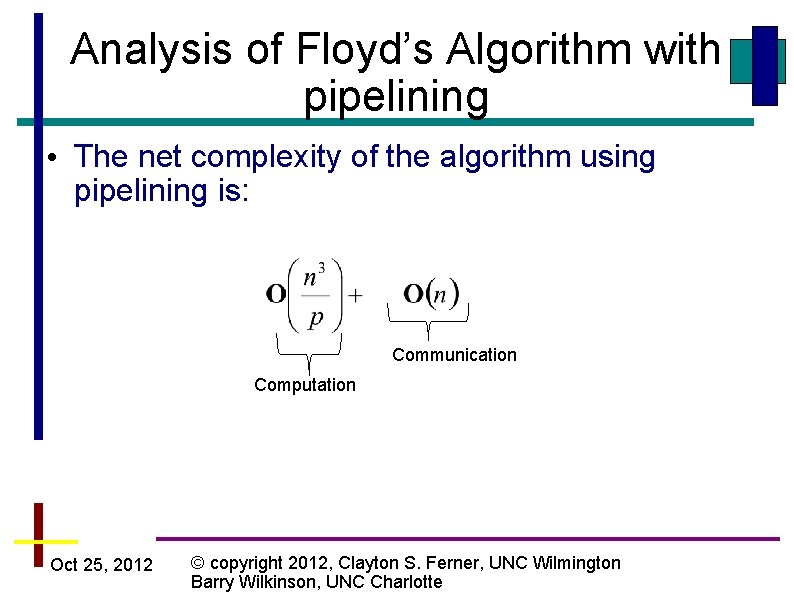
Analysis of Floyd’s Algorithm with pipelining • The net complexity of the algorithm using pipelining is: Communication Computation Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

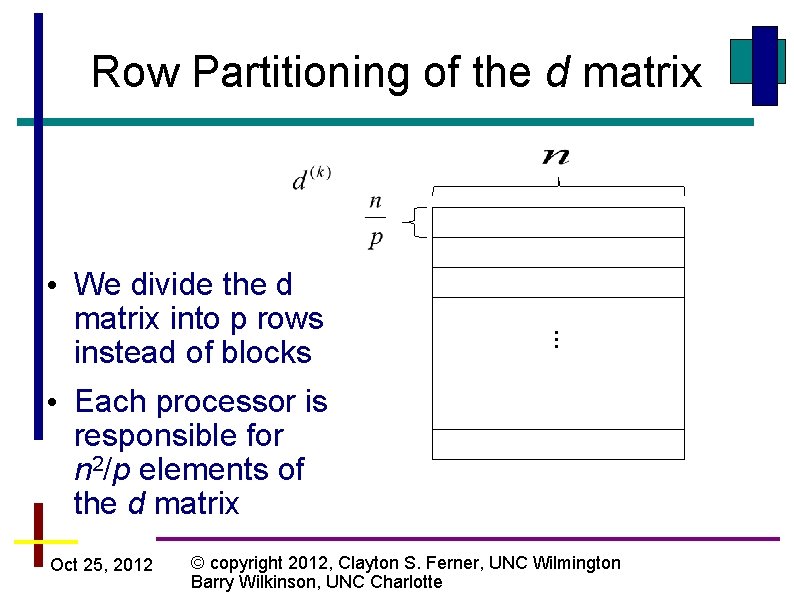
• We divide the d matrix into p rows instead of blocks • Each processor is responsible for n 2/p elements of the d matrix Oct 25, 2012 … Row Partitioning of the d matrix © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

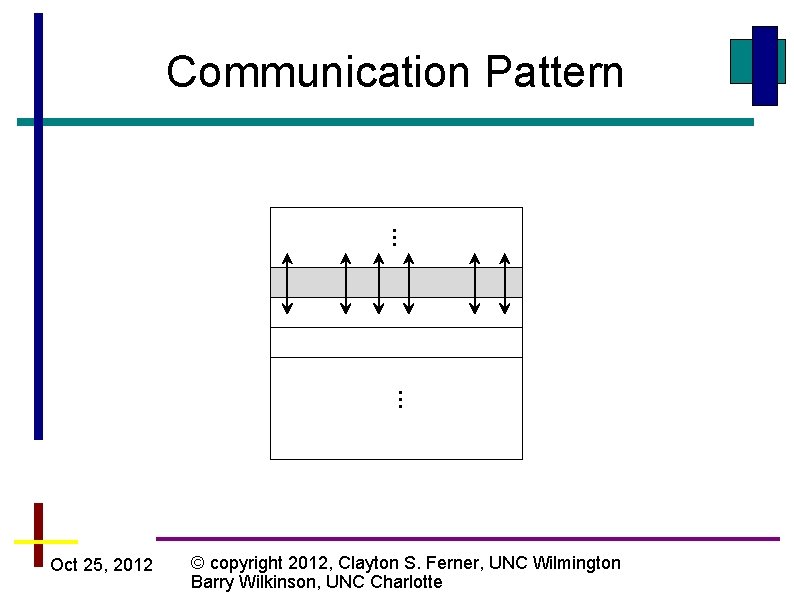
Partitioning of the d matrix k column • Now we are only sending between rows • But this still requires broadcasting or a pipeline Oct 25, 2012 j column k row i row © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

… … Communication Pattern Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

All Pairs using Floyd’s Algorithm Floyd_APSP(V, E, A) V – set of vertices { E – set of edges 0 d i, j = Ai, j for all i, j A – adjacency matrix for k = 1 to n #pragma omp parallel for private (i, j) for i = 1 to n for j = 1 to n d(k)i, j = min(d(k-1)i, j , d(k-1)i, k + d(k-1)k, j ) • Given the amount of communication, this algorithm would best be done on a sharedmemory system Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

Questions Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte