Parallel Application Case Studies Examine Ocean and BarnesHut

Parallel Application Case Studies Examine Ocean and Barnes-Hut and Ray Tracing and Data Mining Assume cache-coherent shared address space Five parts for each application • • • Sequential algorithms and data structures Partitioning Orchestration Mapping Components of execution time on SGI Origin 2000

Application Overview Simulating Ocean Currents • Regular structure, scientific computing Simulating the Evolution of Galaxies • Irregular structure, scientific computing Rendering Scenes by Ray Tracing • Irregular structure, computer graphics Data Mining • Irregular structure, information processing

Case Study 1: Ocean Simulate eddy currents in an ocean basin Problem Domain: Oceanography Representative of: problems in CFD, finite differencing, regular grid problems Algorithms used: SOR, nearest neighbour General Approach: discretize space and time in the simulation. Model ocean basin as a grid of points. All important physical properties like pressure, velocity etc. have values at each grid point Approximations: Use several 2 -D grids at several horizontal crossections of the ocean basin. Assume basin in rectangular, grid points are equally spaced.

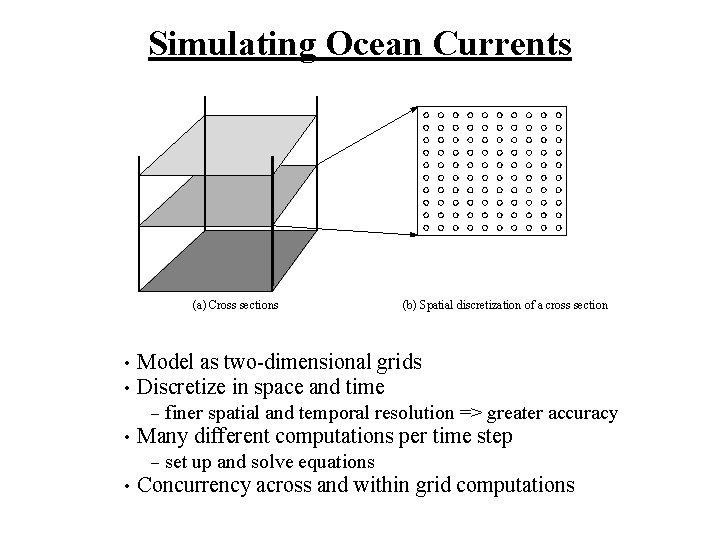
Simulating Ocean Currents (a) Cross sections • • Model as two-dimensional grids Discretize in space and time – • finer spatial and temporal resolution => greater accuracy Many different computations per time step – • (b) Spatial discretization of a cross section set up and solve equations Concurrency across and within grid computations

Ocean Computations in a Time-step:

Partitioning Exploit data parallelism • Function parallelism only to reduce synchronization Static partitioning within a grid computation • Block versus strip – • inherent communication versus spatial locality in communication Load imbalance due to border elements and number of boundaries Solver has greater overheads than other computations

Orchestration and Mapping Spatial Locality similar to equation solver • Except lots of grids, so cache conflicts across grids Complex working set hierarchy A few points for near-neighbor reuse, three subrows, partition of one grid, partitions of multiple grids… • First three or four most important • Large working sets, but data distribution easy • Synchronization Barriers between phases and solver sweeps • Locks for global variables • Lots of work between synchronization events • Mapping: easy mapping to 2 -d array topology or richer

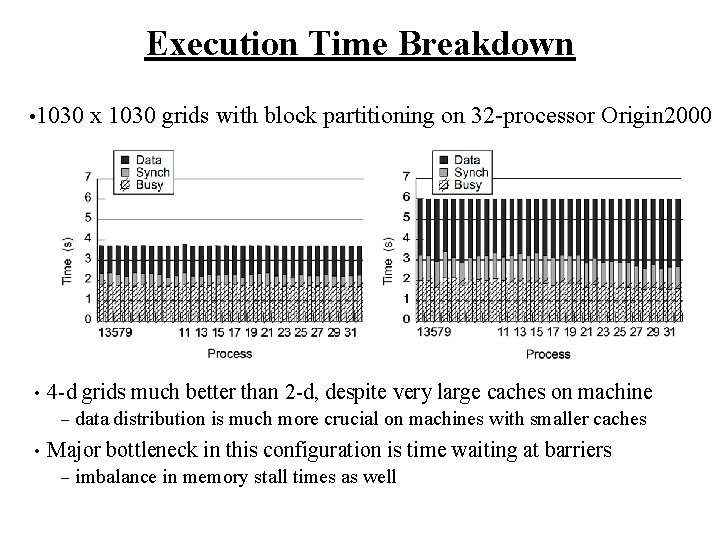
Execution Time Breakdown • 1030 • 4 -d grids much better than 2 -d, despite very large caches on machine – • x 1030 grids with block partitioning on 32 -processor Origin 2000 data distribution is much more crucial on machines with smaller caches Major bottleneck in this configuration is time waiting at barriers – imbalance in memory stall times as well

Case Study 2: Barnes Hut Simulate the evolution of galaxies Problem Domain: Astrophysics Representative of: problems: hierarchical n-body Algorithms used: Barnes Hut General Approach: discretize space and time in the simulation. Represent 3 D space as an oct-tree where each non-leaf node has upto 8 children and all leaf nodes contain one star. For each body traverse the tree starting at the root until a node is reached which represents a cell in space that is far enough from the body that the subtree can be approximated by a single body.

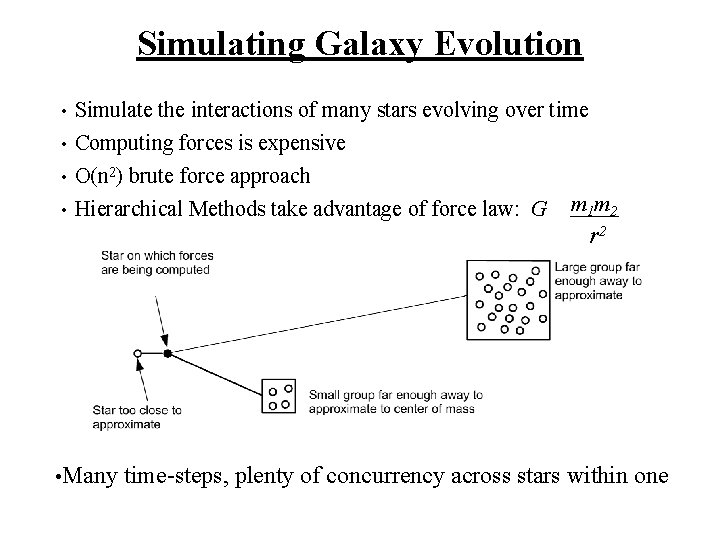
Simulating Galaxy Evolution Simulate the interactions of many stars evolving over time • Computing forces is expensive • O(n 2) brute force approach • Hierarchical Methods take advantage of force law: G m 1 m 2 • r 2 • Many time-steps, plenty of concurrency across stars within one

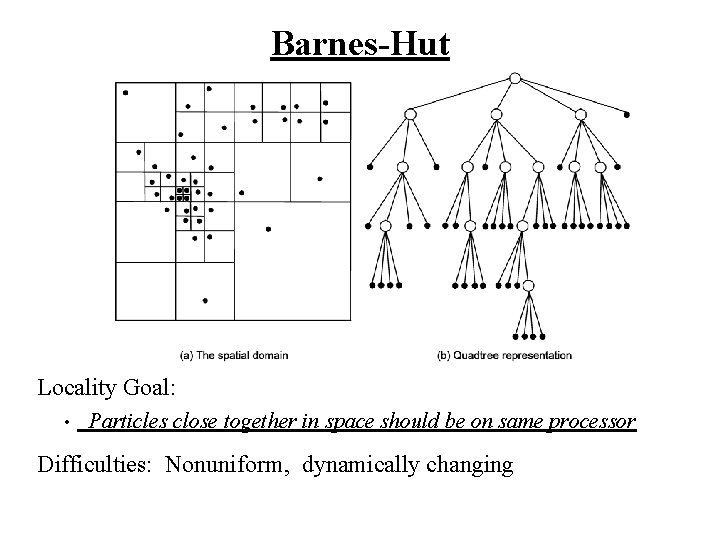
Barnes-Hut Locality Goal: • Particles close together in space should be on same processor Difficulties: Nonuniform, dynamically changing

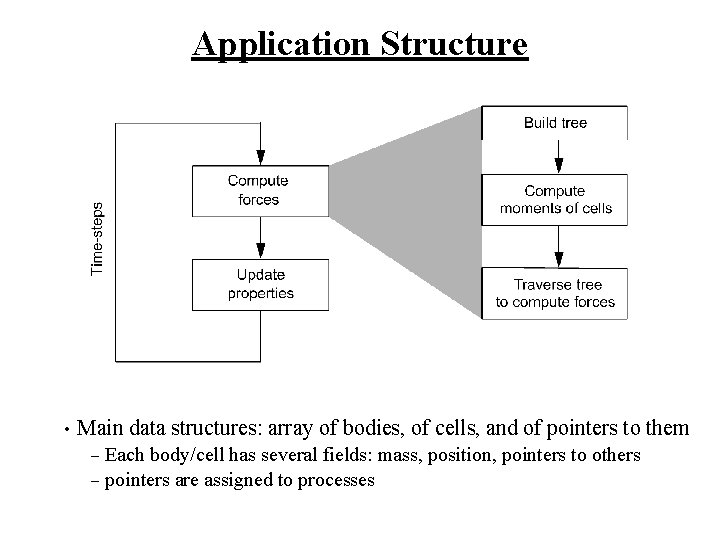
Application Structure • Main data structures: array of bodies, of cells, and of pointers to them Each body/cell has several fields: mass, position, pointers to others – pointers are assigned to processes –

Partitioning Decomposition: bodies in most phases, cells in computing moments Challenges for assignment: • Nonuniform body distribution => work and comm. Nonuniform – • Distribution changes dynamically across time-steps – • Cannot assign statically Information needs fall off with distance from body – • Cannot assign by inspection Partitions should be spatially contiguous for locality Different phases have different work distributions across bodies No single assignment ideal for all – Focus on force calculation phase – • Communication needs naturally fine-grained and irregular

Load Balancing • Equal particles equal work. – • Solution: Assign costs to particles based on the work they do Work unknown and changes with time-steps – Insight : System evolves slowly – Solution: Count work per particle, and use as cost for next time-step. Powerful technique for evolving physical systems

A Partitioning Approach: ORB Orthogonal Recursive Bisection: Recursively bisect space into subspaces with equal work • – Work is associated with bodies, as before Continue until one partition per processor • • High overhead for large no. of processors

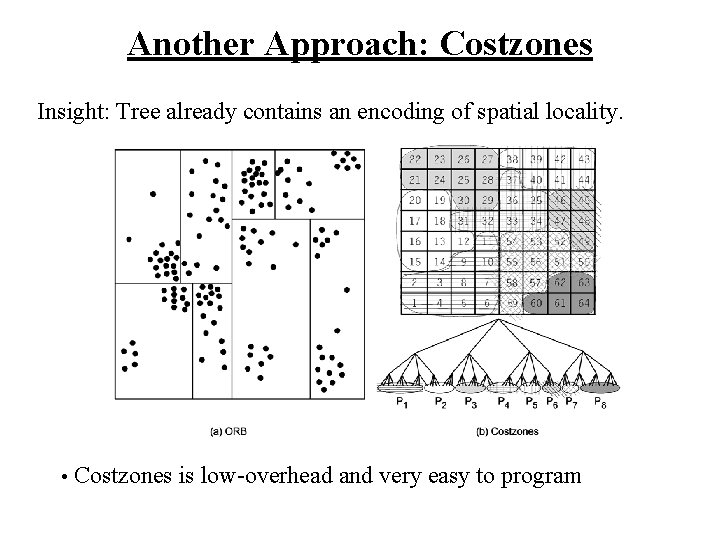
Another Approach: Costzones Insight: Tree already contains an encoding of spatial locality. • Costzones is low-overhead and very easy to program

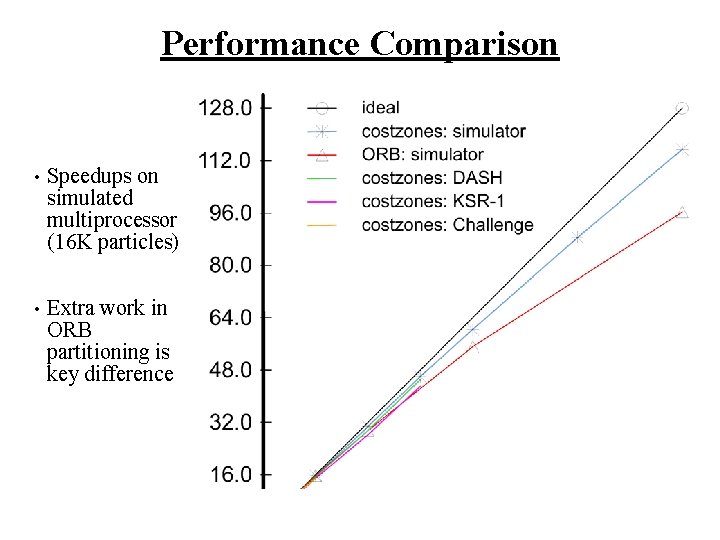
Performance Comparison • Speedups on simulated multiprocessor (16 K particles) • Extra work in ORB partitioning is key difference

Orchestration and Mapping Spatial locality: Very different than in Ocean, like other aspects • Data distribution is much more difficult than Redistribution across time-steps – Logical granularity (body/cell) much smaller than page – Partitions contiguous in physical space does not imply contiguous in array – But, good temporal locality, and most misses logically non-local anyway – • Long cache blocks help within body/cell record, not entire partition Temporal locality and working sets: • Important working set scales as 1/ 2 log n • Slow growth rate, and fits in second-level caches, unlike Ocean Synchronization: • • • Barriers between phases No synch within force calculation: data written different from data read Locks in tree-building, pt. to pt. event synch in center of mass phase Mapping: ORB maps well to hypercube, costzones to linear array

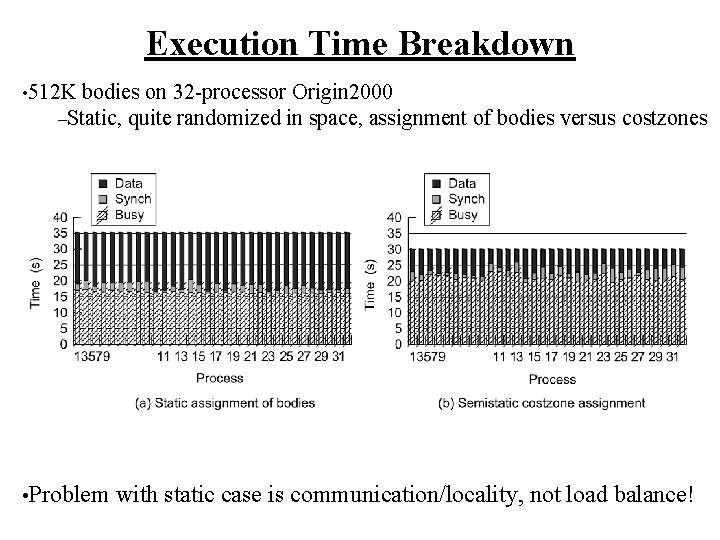
Execution Time Breakdown • 512 K bodies on 32 -processor Origin 2000 –Static, quite randomized in space, assignment • Problem of bodies versus costzones with static case is communication/locality, not load balance!

Case Study 3: Ray. Trace Render a 3 D scene on a 2 D image plane. Problem Domain: Computer Graphics General Approach: Shoot rays through the pixels in an image plane into a 3 D scene and trace the rays as they bounce around (reflect, refract etc. ) and conpute the color and opacity for the corresponding pixels.

Rendering Scenes by Ray Tracing Shoot rays into scene through pixels in image plane • Follow their paths • they bounce around as they strike objects – they generate new rays: ray tree per input ray – Result is color and opacity for that pixel • Parallelism across rays •

Raytrace Rays shot through pixels in image are called primary rays Reflect and refract when they hit objects • Recursive process generates ray tree per primary ray • Hierarchical spatial data structure keeps track of primitives in scene • Nodes are space cells, leaves have linked list of primitives Tradeoffs between execution time and image quality

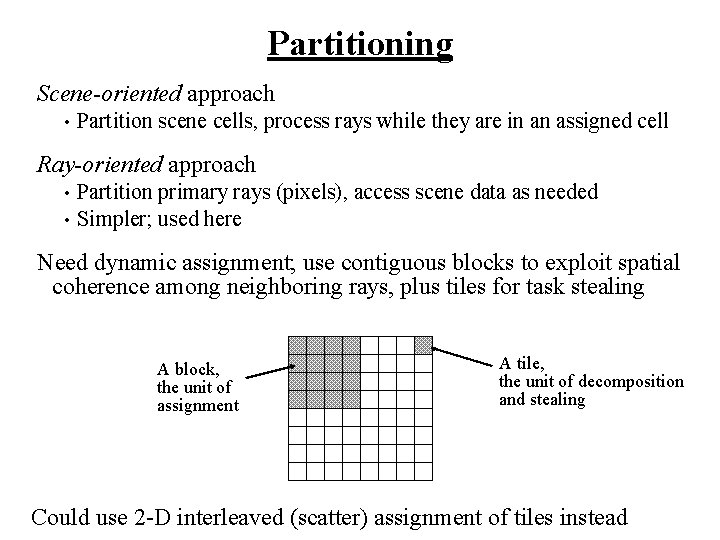
Partitioning Scene-oriented approach • Partition scene cells, process rays while they are in an assigned cell Ray-oriented approach • • Partition primary rays (pixels), access scene data as needed Simpler; used here Need dynamic assignment; use contiguous blocks to exploit spatial coherence among neighboring rays, plus tiles for task stealing A block, the unit of assignment A tile, the unit of decomposition and stealing Could use 2 -D interleaved (scatter) assignment of tiles instead

Orchestration and Mapping Spatial locality Proper data distribution for ray-oriented approach very difficult • Dynamically changing, unpredictable access, fine-grained access • Better spatial locality on image data than on scene data • – Strip partition would do better, but less spatial coherence in scene access Temporal locality Working sets much larger and more diffuse than Barnes-Hut • But still a lot of reuse in modern second-level caches • – SAS program does not replicate in main memory Synchronization: • One barrier at end, locks on task queues Mapping: natural to 2 -d mesh for image, but likely not important

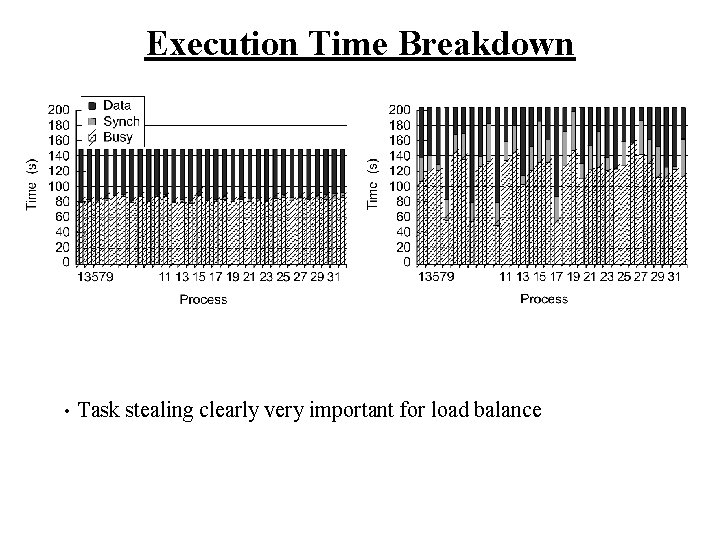
Execution Time Breakdown • Task stealing clearly very important for load balance

Case Study 4: Data Mining Identify trends or associations in data gathered by a business. Problem Domain: Database Systems. General Approach: Examine the database and determine which sets of k items are found to occur together in more than a certain threshold of the transactions. Determine association rules given these itemsets and their frequency.

Basics Itemset: A set of items that occur together in a transaction. Large Itemset: An itemset that is found to occur in more than a threshold fraction of transactions. Goal: Discover the large itemsets of size k and their frequencies of occurance in the database. Algorithm: Determine large itemsets of size one. Given large itemset of size n-1, construct a candidate list of itemsets of size m Verify the frequencies of the itemsets in the candidate list to discover the large itemsets of size n. Continue until size = k

Where’s the Parallelism Examining large itemsets of size n-1 to determine candidate sets of size n (1< n <=k) Counting the number of transactions in the database that countain each of the candidate itemsets. What’s the bottleneck? Disk access: database typically is much larger than memory => data has to be accessed from disk As number of processes increase, disk can become more of a bottleneck. Goal actually is to minimize disk access during execution.

Example Items in Database: A, B, C, D, E Items within a transactions are lexicographically sorted: e. g. T 1 = {A, B, E} Items within itemsets are also lexicographically sorted. Let the large itemset of size two be {AB, AC, AD, BC, BD, CD, DE} Candidate list of size three = {ABC, ABD, ACD, BCD} Now search through all transactions to calculate frequencies to find large itemset of size three.

Optimizations Store transactions by itemset: e. g. AD = {T 1, T 5, T 7…} Exploit equivalence classes: Itemsets of size n-1 that have common (n -2)-sized prefixes form equivalence classes. Itemsets of size n can only be formed from the equivalence classes of size n-1. Equivalence classes are disjoint.

Parallelization(Phase 1) Computing the 1 -equivalence classes and large itemsets of size 2: done by partioning the database among processes Each process computes a local frequency value for each itemset of size 2. Compute global frequency values from local process values. Use global frequency values to compute equivalence classes. Transform the database format from per-transaction to per-itemset format. Each process does a partial transformation for its partition of the database Communicate transformations to other processes to form a complete transformation.

Parallelization(Phase 2) Partitioning: Divide the 1 -equivalence classes among processes. Disk accesses: Use local disk as far as possible to store subsequently generated equivalence classes. Load balancing: static distribution (maybe with some heuristics) with possible task stealing if required. Communication and Synchronization overhead: None unless task stealing is required. Remote Disk accesses: None (unless task stealing required). Spatial Locality: ensured by lexicographic ordering. Temporal Locality: Ensured by proceeding over one equilence class over time.