Parallel and Perpendicular Lines Using Slope Big Ideas

Parallel and Perpendicular Lines Using Slope Big Ideas Geometry Section 3. 5

Auxiliary Lines Review 21° 87° 1

Auxiliary Lines Review (Solution) 21° 87° 66° m∠ 1 = 66° 1

Algebra 1 Refresher � Linear equations can be written in three ways ◦ Standard Form: ax + by = c, where a > 0 ◦ Slope-Intercept Form: y = mx + b (everyone’s favorite form) ◦ Point-Slope Form y – y 1 = m(x – x 1) �m stands for the slope of the line ◦ slope = rate of change (the change of y over the change of x) ◦ Given two points (x 1, y 1) (x 2, y 2) we can find the slope using m= y 2 – y 1 x 2 – x 1

Algebra 1 Refresher � Write an equation of the line that goes through (1, 1) and (2, 4) Slope m= m= y-intercept 4– 1 2– 1 y = mx + b 3 1 = 3(1) + b 1 -2 = b m=3 Thus, y = 3 x - 2

The Biconditional Statement � Biconditional Statement: a statement that is written in the if and only if form by using a conditional statement and its converse � Example ◦ Conditional Statement: If two line segments are the same length, then they are congruent ◦ Converse: If two line segments are congruent, then they are the same length ◦ Biconditional Statement: Two line segments are the same length if and only if they are congruent

Slopes of Parallel Lines Theorem � In a coordinate plane, two distinct nonvertical lines are parallel if and only if they have the same slope ◦ remember vertical lines have undefined slope � Any two distinct vertical lines are parallel y 2 = m 2 + b 2 y 1 = m 1 + b 1 will be parallel if m 1 = m 2 and b 1 ≠ b 2

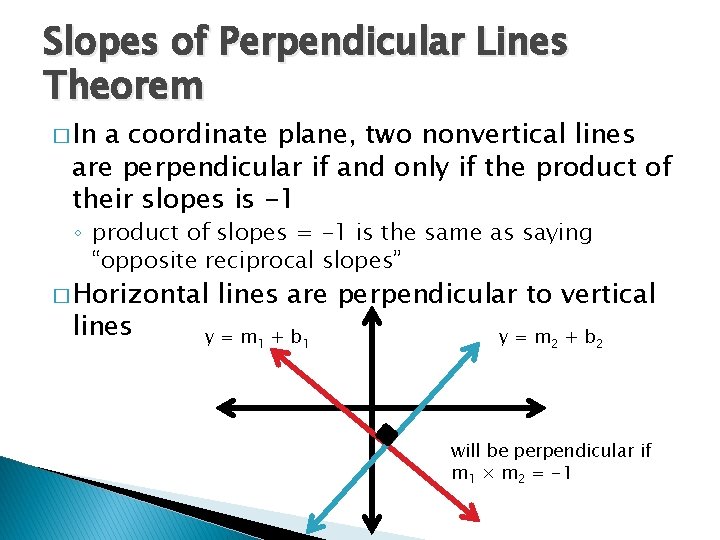
Slopes of Perpendicular Lines Theorem � In a coordinate plane, two nonvertical lines are perpendicular if and only if the product of their slopes is -1 ◦ product of slopes = -1 is the same as saying “opposite reciprocal slopes” � Horizontal lines are perpendicular to vertical y = m 1 + b 1 y = m 2 + b 2 will be perpendicular if m 1 × m 2 = -1

Write an Equation of a Parallel Line � Write an equation of the line passing through the point (-1, 1) that is parallel to the line y = 2 x – 3 � The slope of this line is 2, so the line parallel to it must also have slope 2. Thus m = 2 y = mx + b 1 = 2(-1) + b 1 = -2 + b 3=b The parallel equation is y = 2 x + 3

Write an Equation of a Perpendicular Line � Write an equation of the line passing through the point (2, 3) that is perpendicular to line 2 x + y = 2 y = -2 x + 2 so the perpendicular slope is m = ½ because -2 × ½ = -1 y = mx + b 3 = ½ (2) + b 3 = 1+ b 2=b The perpendicular equation is y = ½ x + 2

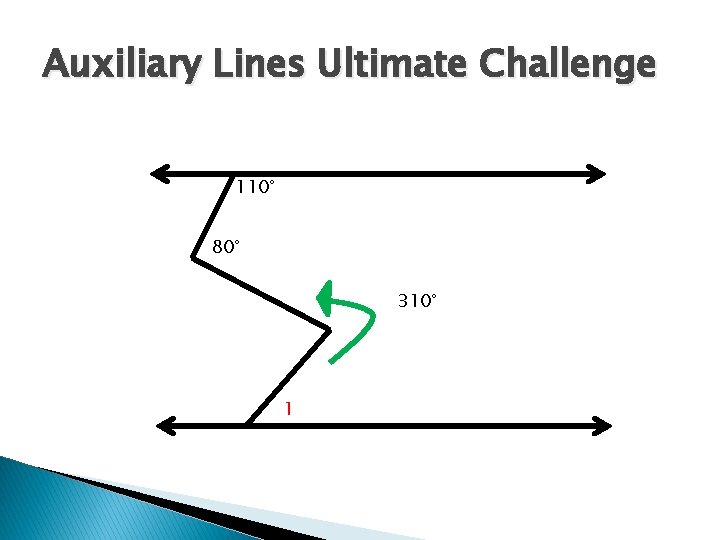
Auxiliary Lines Ultimate Challenge 110° 80° 310° 1

Bibliography � Big Ideas Geometry � Eureka Math Geometry