Parallel and Perpendicular Lines Presented By Mr Laws

Parallel and Perpendicular Lines Presented By Mr. Laws Math I, JCMS

Goals/Standards • G. GPE. 5 Prove the slope criteria for parallel and perpendicular lines and use them to solve geometric problems (e. g. , find the equation of a line parallel or perpendicular to a given line that passes through a given point)

Essential Question: • Using math principles, how do I find the equation of a line parallel or perpendicular to a given line that passes through a given point?

Target Statement: • I CAN find the equation of a line parallel or perpendicular to a given line that passes through a given point.

Parallel and Perpendicular Lines • Parallel Lines – are two lines that are parallel (║) with the same slopes. • Perpendicular Lines – are two lines that are perpendicular (┴) to each other (crosses at a 900 angle) and one slope is multiply by -1.

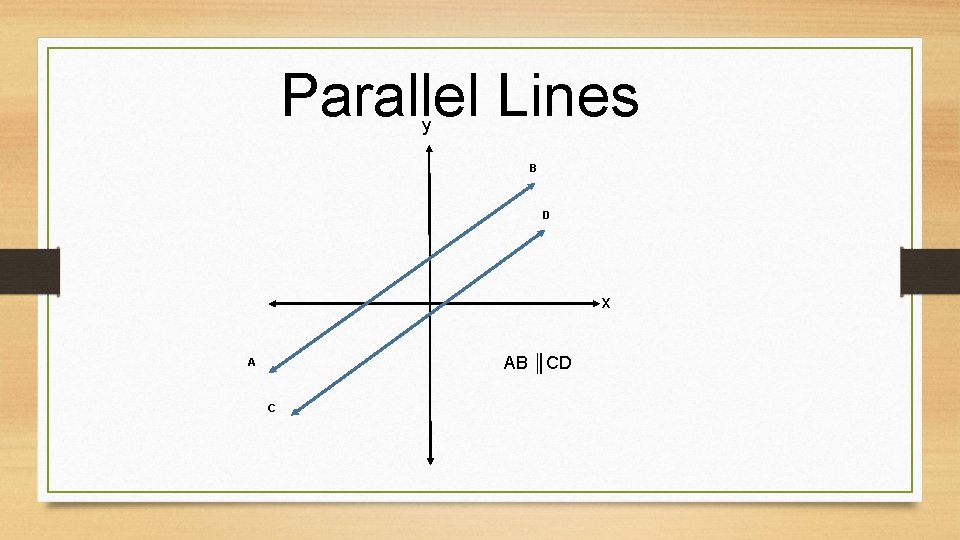
Parallel Lines y B D x AB ║CD A C

How do I write in slope intercept form a line that is parallel to a linear equation when given a point? Ex. 1 Step 1: Label points X 1 and Y 1. X 1 Y 1. (-2, -2); parallel to y = 2 x y – (-2) = 2(x – (-2)) y + 2 = 2 x + 4 -2 Answer: y = 2 x + 2 -2 Step 2: Identify the slope of the linear equation and substitute it in point slope form (y –y 1=m(x – x 1) Step 3: Using PSF, solve and write the linear equation that is parallel to y = 2 x.

How do I write in standard form a line that is parallel to a linear equation when given a point? Ex. 2 X 1 Y 1. Step 1: Label points X 1 and Y 1. Step 2: Identify the slope of the linear equation and substitute it in point slope form (y –y 1=m(x – x 1) -4 -4

How do I write in standard form a line that is parallel to a linear equation when given a point? Ex. 2 ● 4 Step 4: Multiply each side by 4. ● 4 4 y = -3 x – 4 +3 x 3 x + 4 y = -4 Step 5: Add 3 x on both sides Step 6: Check to see if equation is in standard form.

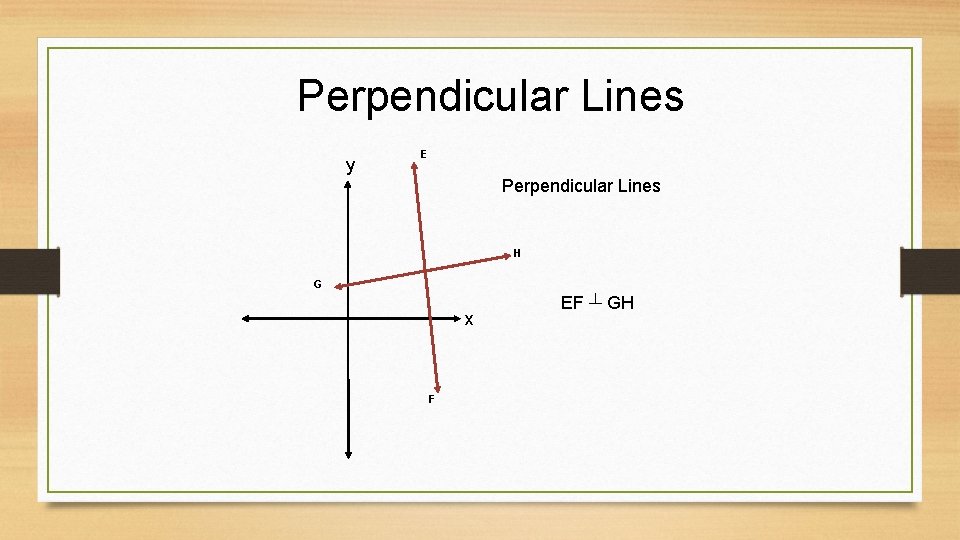
Perpendicular Lines y E Perpendicular Lines H G x F EF ┴ GH

How do I write in slope intercept form a line that is perpendicular to a linear equation when given a point? Ex. 3 Step 1: Label points X 1 and Y 1. X 1 Y 1. (-2, -2); perpendicular to y = 2 x -2 Step 2: Identify the slope of the linear equation and substitute it in point slope form (y –y 1=m(x – x 1) -2 Answer: Step 4 Write equation in slope intercept form the equation that is perpendicular to y = 2 x.

How do I write in standard form a line that is perpendicular to a linear equation when given a point? Ex. 4 Step 1: Label points X 1 and Y 1. X 1 Y 1. Step 2: Identify the slope of the linear equation and substitute it in point slope form (y –y 1=m(x – x 1) y – (-2) = -2( x – 2) y + 2 = -2 x + 4 -2 -2 y = -2 x + 2

How do I write in standard form a line that is perpendicular to a linear equation when given a point? Ex. 4 Step 4: Add 2 x on both sides y = -2 x + 2 +2 x Answer: 2 x + y = 2 Step 5: Check to see if equation is in standard form.

How do I find an equation of a line that is perpendicular with a given point and in standard form? Ex. 5: Find the equation of a line that is perpendicular to the graph of 4 x + 3 y = 9 and passes through (-2, 3)? Step 1: Change the equation to slope intercept form. 4 x + 3 y = -4 x 9 3 y = -4 x + 93 3 Step 2: Subtract 4 x on both sides of the equation. Step 3: Divide 3 on both sides of the equation.

How do I find an equation of a line that is perpendicular with a given point and in standard form? Ex. 5: Find the equation of a line that is perpendicular to the graph of 4 x + 3 y = 9 and passes through (-2, 3)? x y Step 4: Label points X 1 and Y 1 1 1 (-2, 3) Step 6: Substitute the slope and the point into the point slope formula. Simplify

How do I find an equation of a line that is perpendicular with a given point and in standard form? Ex. 5: Find the equation of a line that is perpendicular to the graph of 4 x + 3 y = 9 and passes through (-2, 3)? Step 7: Change the equation from point slope form to slope intercept form. Step 8: Add 3 on both sides of the +3 equation. +3 or What is the equation in standard form? 3 x – 4 y = - 18

Your Turn 1. What is the equation of the line that passes through point (12, 10) and is parallel to y = 3 x + 6? What is the equation that is perpendicular to the given point? 2. Which equation represents the line that passes through the point (4, -5) and is perpendicular to the line x + 2 y = 5? a. x – 2 y = -14 b. x + 2 y = -6 c. 2 x +y = 3 d. 2 x – y = 13

Summary • What are some important concepts to remember about this lesson? • Are there any other information you would like to learn about the lesson? • Can you answer the essential question at the beginning of the lesson?