Parallel Algorithms Continued Patrick Cozzi University of Pennsylvania

Parallel Algorithms Continued Patrick Cozzi University of Pennsylvania CIS 565 - Spring 2012

Announcements n Presentation topics due tomorrow, 02/07 n Homework 2 due next Monday, 02/13

Agenda n Parallel Algorithms ¨ Review Stream Compression ¨ Radix Sort n CUDA Performance

Radix Sort n Efficient for small sort keys ¨ k-bit keys require k passes

Radix Sort Each radix sort pass partitions its input based on one bit n First pass starts with the least significant bit (LSB). Subsequent passes move towards the most significant bit (MSB) n MSB 010 LSB

Radix Sort n Example input: 100 111 010 110 011 101 000 Example from http: //http. developer. nvidia. com/GPUGems 3/gpugems 3_ch 39. html

Radix Sort n First pass: partition based on LSB 100 111 010 110 011 101 000 100 010 110 000 111 011 101 001 LSB == 0 LSB == 1

Radix Sort n Second pass: partition based on middle bit 100 111 010 110 011 101 000 100 010 110 000 111 011 101 001 100 000 101 010 111 011 bit == 0 bit == 1

Radix Sort n Final pass: partition based on MSB 100 111 010 110 011 101 000 100 010 110 000 111 011 101 001 100 000 101 010 111 000 001 010 011 100 101 110 111 MSB == 0 MSB == 1

Radix Sort n Completed: 100 111 010 110 011 101 000 100 010 110 000 111 011 101 001 100 000 101 010 111 000 001 010 011 100 101 110 111

Radix Sort n Completed: 4 7 2 6 3 5 1 0 4 2 6 0 7 3 5 1 4 0 5 1 2 6 7 3 0 1 2 3 4 5 6 7

Parallel Radix Sort n Where is the parallelism?

Parallel Radix Sort 1. Break input arrays into tiles ¨ Each 2. 3. tile fits into shared memory for an SM Sort tiles in parallel with radix sort Merge pairs of tiles using a parallel bitonic merge until all tiles are merged. Our focus is on Step 2

Parallel Radix Sort n Where is the parallelism? ¨ Each tile is sorted in parallel ¨ Where is the parallelism within a tile?

Parallel Radix Sort n Where is the parallelism? ¨ Each tile is sorted in parallel ¨ Where is the parallelism within a tile? Each pass is done in sequence after the previous pass. No parallelism n Can we parallelize an individual pass? How? n ¨ Merge also has parallelism

Parallel Radix Sort n Implement spilt. Given: ¨ Array, 100 ¨ Array, 0 n i, at pass b: 111 010 110 011 101 000 b, which is true/false for bit b: 1 0 0 1 1 1 0 Output array with false keys before true keys: 100 010 110 000 111 011 101 001

Parallel Radix Sort n Step 1: Compute e array 100 111 010 110 011 101 000 i array 0 1 0 0 1 1 1 0 b array 1 0 1 1 0 0 0 1 e array

Parallel Radix Sort n Step 2: Exclusive Scan e 100 111 010 110 011 101 000 i array 0 1 0 0 1 1 1 0 b array 1 0 1 1 0 0 0 1 e array 0 1 1 2 3 3 f array

Parallel Radix Sort n Step 3: Compute total. Falses 100 111 010 110 011 101 000 i array 0 1 0 0 1 1 1 0 b array 1 0 1 1 0 0 0 1 e array 0 1 1 2 3 3 f array total. Falses = e[n – 1] + f[n – 1] total. Falses = 1 + 3 total. Falses = 4

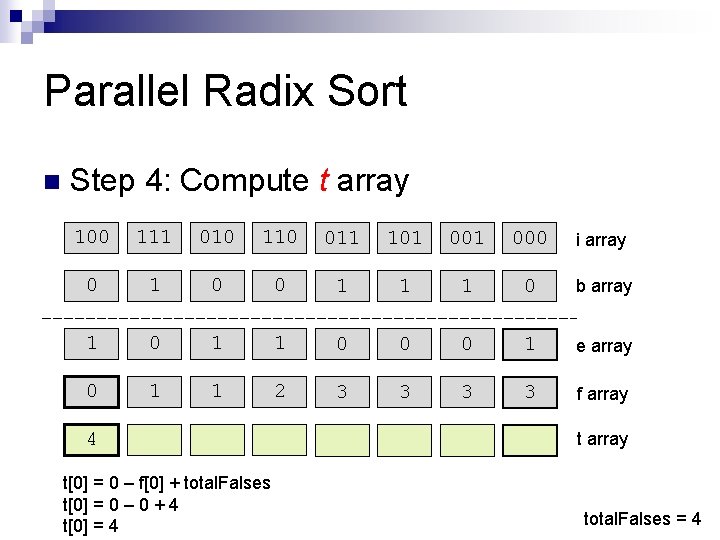
Parallel Radix Sort n Step 4: Compute t array 100 111 010 110 011 101 000 i array 0 1 0 0 1 1 1 0 b array 1 0 1 1 0 0 0 1 e array 0 1 1 2 3 3 f array t[i] = i – f[i] + total. Falses = 4

Parallel Radix Sort n Step 4: Compute t array 100 111 010 110 011 101 000 i array 0 1 0 0 1 1 1 0 b array 1 0 1 1 0 0 0 1 e array 0 1 1 2 3 3 f array 4 t[0] = 0 – f[0] + total. Falses t[0] = 0 – 0 + 4 t[0] = 4 t array total. Falses = 4

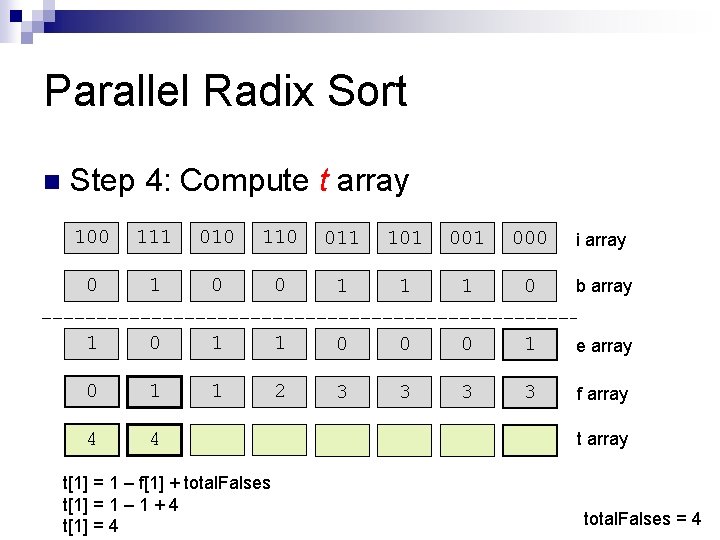
Parallel Radix Sort n Step 4: Compute t array 100 111 010 110 011 101 000 i array 0 1 0 0 1 1 1 0 b array 1 0 1 1 0 0 0 1 e array 0 1 1 2 3 3 f array 4 4 t[1] = 1 – f[1] + total. Falses t[1] = 1 – 1 + 4 t[1] = 4 t array total. Falses = 4

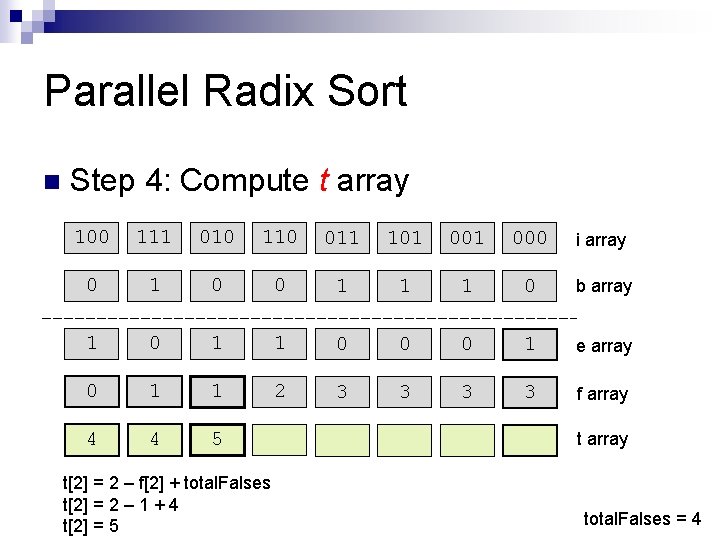
Parallel Radix Sort n Step 4: Compute t array 100 111 010 110 011 101 000 i array 0 1 0 0 1 1 1 0 b array 1 0 1 1 0 0 0 1 e array 0 1 1 2 3 3 f array 4 4 5 t[2] = 2 – f[2] + total. Falses t[2] = 2 – 1 + 4 t[2] = 5 t array total. Falses = 4

Parallel Radix Sort n Step 4: Compute t array 100 111 010 110 011 101 000 i array 0 1 0 0 1 1 1 0 b array 1 0 1 1 0 0 0 1 e array 0 1 1 2 3 3 f array 4 4 5 5 5 6 7 8 t array t[i] = i – f[i] + total. Falses = 4

Parallel Radix Sort n Step 5: Scatter based on address d 100 111 010 110 011 101 000 i array 0 1 0 0 1 1 1 0 b array 1 0 1 1 0 0 0 1 e array 0 1 1 2 3 3 f array 4 4 5 5 5 6 7 8 t array 0 d[i] = b[i] ? t[i] : f[i]

Parallel Radix Sort n Step 5: Scatter based on address d 100 111 010 110 011 101 000 i array 0 1 0 0 1 1 1 0 b array 1 0 1 1 0 0 0 1 e array 0 1 1 2 3 3 f array 4 4 5 5 5 6 7 8 t array 0 4 d[i] = b[i] ? t[i] : f[i]

Parallel Radix Sort n Step 5: Scatter based on address d 100 111 010 110 011 101 000 i array 0 1 0 0 1 1 1 0 b array 1 0 1 1 0 0 0 1 e array 0 1 1 2 3 3 f array 4 4 5 5 5 6 7 8 t array 0 4 1 d[i] = b[i] ? t[i] : f[i]

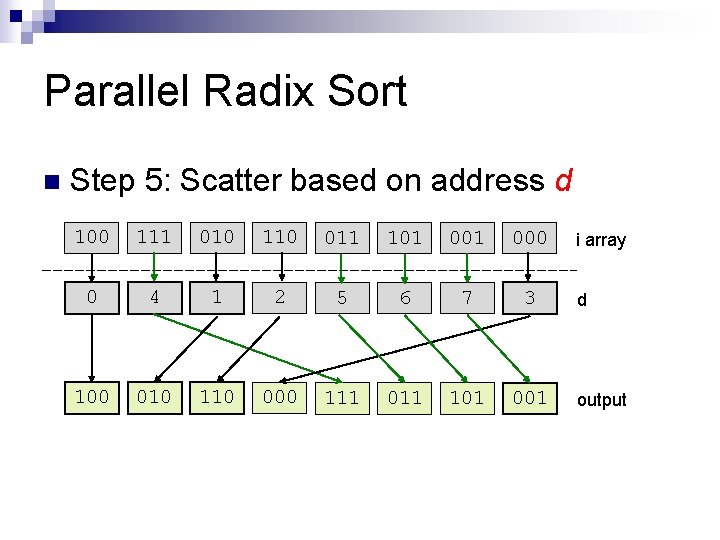
Parallel Radix Sort n Step 5: Scatter based on address d 100 111 010 110 011 101 000 i array 0 1 0 0 1 1 1 0 b array 1 0 1 1 0 0 0 1 e array 0 1 1 2 3 3 f array 4 4 5 5 5 6 7 8 t array 0 4 1 2 5 6 7 3 d[i] = b[i] ? t[i] : f[i]

Parallel Radix Sort n Step 5: Scatter based on address d 100 111 010 110 011 101 000 0 4 1 2 5 6 7 3 i array d output

Parallel Radix Sort n Step 5: Scatter based on address d 100 111 010 110 011 101 000 0 4 1 2 5 6 7 3 100 010 110 000 111 011 101 001 i array d output

Parallel Radix Sort n Given k-bit keys, how do we sort using our new split function? n Once each tile is sorted, how do we merge tiles to provide the final sorted array?