Parallel Algorithms chap 30 1 st edition Parallel

Parallel Algorithms (chap. 30, 1 st edition) • Parallel: perform more than one operation at a time. • PRAM model: Parallel Random Access Model. p 0 p 1 Shared memory Multiple processors connected to a shared memory. Each processor access any location in unit time. All processors can access memory in parallel. All processors can perform operations in parallel. pn-1 1

Concurrent vs. Exclusive Access • Four models – – EREW: exclusive read and exclusive write CREW: concurrent read and exclusive write ERCW: exclusive read and concurrent write CRCW: concurrent read and concurrent write • Handling write conflicts – Common-write model: only if they write the same value. – Arbitrary-write model: an arbitrary one succeeds. – Priority-write model: the one with smallest index succeeds. • EREW and CRCW are most popular. 2

Synchronization and Control • Synchronization: – A most important and complicated issue – Suppose all processors are inherently tightly synchronized: • All processors execute the same statements at the same time • No race among processors, i. e, same pace. • Termination control of a parallel loop: – Depend on the state of all processors – Can be tested in O(1) time. 3

Pointer Jumping –list ranking • Given a single linked list L with n objects, compute, for each object in L, its distance from the end of the list. • Formally: suppose next is the pointer field – d[i]= – 0 if next[i]=nil d[next[i]]+1 if next[i] nil • Serial algorithm: (n). 4

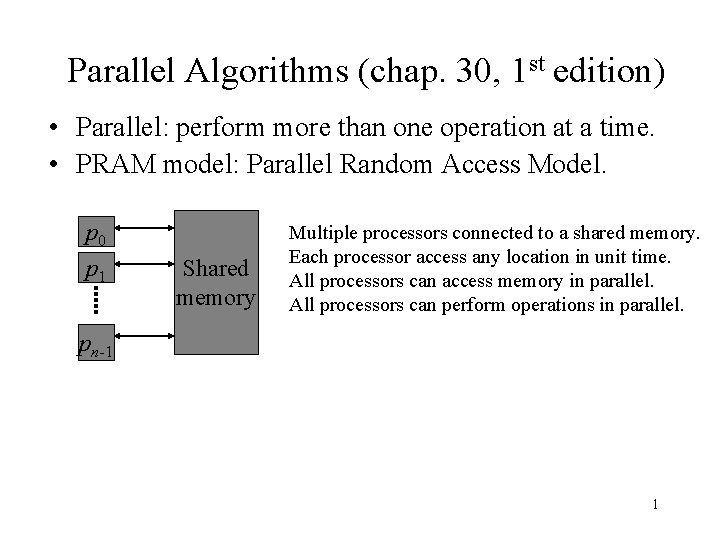
List ranking –EREW algorithm • LIST-RANK(L) (in O(lg n) time) 1. for each processor i, in parallel 2. do if next[i]=nil 3. then d[i] 0 4. else d[i] 1 5. while there exists an object i such that next[i] nil 6. do for each processor i, in parallel 7. do if next[i] nil 8. then d[i]+ d[next[i]] 9. next[i]] 5

List-ranking –EREW algorithm (a) 3 1 4 1 6 1 1 1 0 1 5 0 (b) 3 2 4 2 6 2 1 2 0 1 5 (c) 3 4 4 4 6 3 1 2 0 1 (d) 3 5 4 4 6 3 1 2 0 1 0 0 0 5 5 6

List ranking –correctness of EREW algorithm • Loop invariant: for each i, the sum of d values in the sublist headed by i is the correct distance from i to the end of the original list L. • Parallel memory must be synchronized: the reads on the right must occur before the wirtes on the left. Moreover, read d[i] and then read d[next[i]]. • An EREW algorithm: every read and write is exclusive. For an object i, its processor reads d[i], and then its precedent processor reads its d[i]. Writes are all in distinct locations. 7

LIST ranking EREW algorithm running time • O(lg n): – The initialization for loop runs in O(1). – Each iteration of while loop runs in O(1). – There are exactly lg n iterations: • Each iteration transforms each list into two interleaved lists: one consisting of objects in even positions, and the other odd positions. Thus, each iteration double the number of lists but halves their lengths. – The termination test in line 5 runs in O(1). – Define work =#processors running time. O(n lg n). 8

Parallel prefix on a list • A prefix computation is defined as: – – Input: <x 1, x 2, …, xn> Binary associative operation Output: <y 1, y 2, …, yn> Such that: • y 1 = x 1 • yk= yk-1 xk for k=2, 3, …, n , i. e, yk= x 1 x 2 … xk. – Suppose <x 1, x 2, …, xn> are stored orderly in a list. – Define notation: [i, j]= xi xi+1 … xj 9

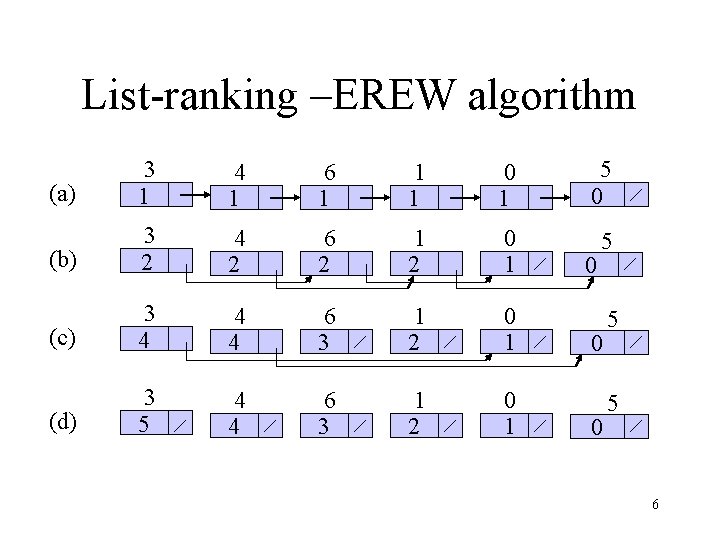
Prefix computation • LIST-PREFIX(L) 1. for each processor i, in parallel 2. do y[i] x[i] 3. while there exists an object i such that next[i] nil 4. do for each processor i, in parallel 5. do if next[i] nil 6. then y[next[i]] y[i] y[next[i]] 7. next[i]] 10

Prefix computation –EREW algorithm (a) (b) (c) (d) x 1 x 2 x 3 x 4 x 5 x 6 [1, 1] [2, 2] [3, 3] [4, 4] [5, 5] [6, 6] x 1 x 2 x 4 x 5 x 6 [1, 1] x 3 [1, 2] [2, 3] [3, 4] [4, 5] x 1 x 2 [1, 1] x 3 [1, 2] [1, 3] x 1 x 2 x 3 [1, 1] [1, 2] [1, 3] [1, 4] [5, 6] x 5 x 6 [2, 5] [3, 6] x 5 x 6 [1, 5] [1, 6] 11

Find root –CREW algorithm • Suppose a forest of binary trees, each node i has a pointer parent[i]. • Find the identity of the tree of each node. • Assume that each node is associated a processor. • Assume that each node i has a field root[i]. 12

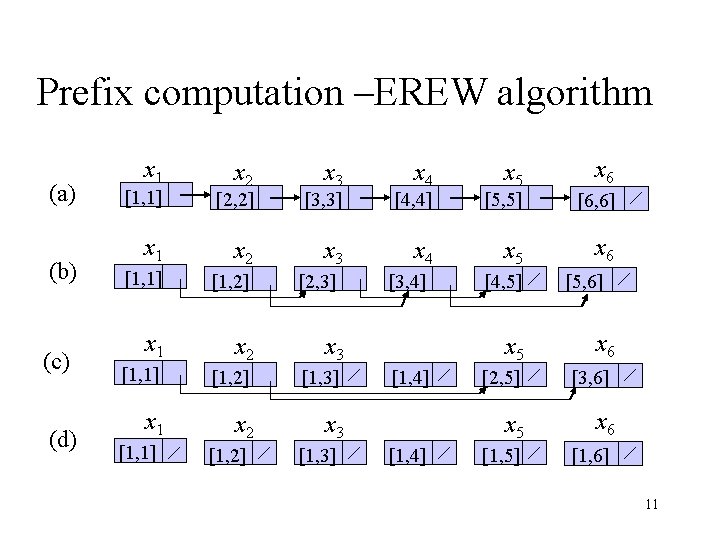
Find-roots –CREW algorithm • FIND-ROOTS(F) 1. for each processor i, in parallel 2. do if parent[i] = nil 3. then root[i] i 4. while there exist a node i such that parent[i] nil 5. do for each processor i, in parallel 6. do if parent[i] nil 7. then root[i] root[parent[i]] 8. parent[i]] 13

Find root –CREW algorithm • Running time: O(lg d), where d is the height of maximum-depth tree in the forest. • All the writes are exclusive • But the read in line 7 is concurrent, since several nodes may have same node as parent. • See figure 30. 5. 14

15

Find roots –CREW vs. EREW • How fast can n nodes in a forest determine their roots using only exclusive read? (lg n) Argument: when exclusive read, a given peace of information can only be copied to one other memory location in each step, thus the number of locations containing a given piece of information at most doubles at each step. Looking at a forest with one tree of n nodes, the root identity is stored in one place initially. After the first step, it is stored in at most two places; after the second step, it is Stored in at most four places, …, so need lg n steps for it to be stored at n places. So CREW: O(lg d) and EREW: (lg n). If d=2(lg n), CREW outperforms any EREW algorithm. If d= (lg n), then CREW runs in O(lg lg n), and EREW is much slower. 16

Find maximum – CRCW algorithm • • • Given n elements A[0, n-1], find the maximum. Suppose n 2 processors, each processor (i, j) compare A[i] and A[j], for 0 i, j n-1. FAST-MAX(A) 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. n length[A] for i 0 to n-1, in parallel do m[i] true for i 0 to n-1 and j 0 to n-1, in parallel do if A[i] < A[j] then m[i] false for i 0 to n-1, in parallel do if m[i] =true then max A[i] return max A[j] 5 6 9 2 9 m 5 F TT FT F A[i] 6 F F T F 9 F FF F F T 2 TTT F 9 F FF F F T max=9 The running time is O(1). Note: there may be multiple maximum values, so their processors Will write to max concurrently. Its work = n 2 O(1) =O(n 2). 17

Find maximum –CRCW vs. EREW • If find maximum using EREW, then (lg n). • Argument: consider how many elements “think” that they might be the maximum. – First, n, – After first step, n/2, – After second step n/4. …, each step, halve. • Moreover, CREW takes (lg n). 18

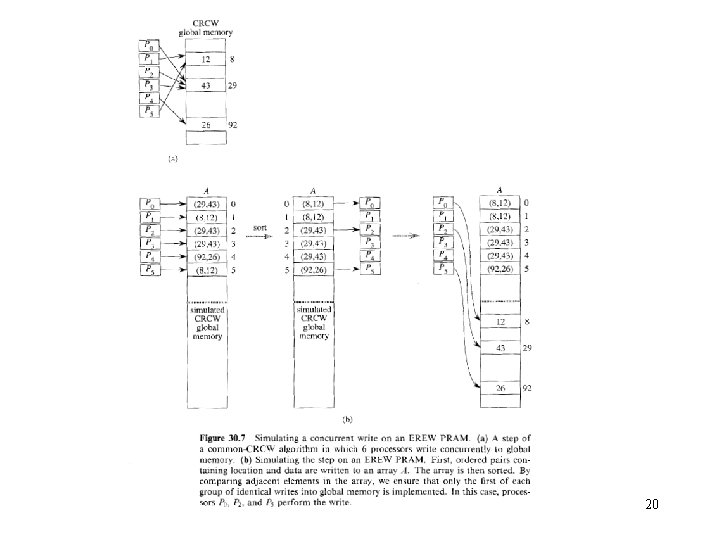
Stimulating CRCW with EREW • Theorem: – A p-processor CRCW algorithm can be no more than O(lg p) times faster than a best p-processor EREW algorithm for the same problem. • Proof: each step of CRCW can be simulated by O(lg p) computations of EREW. – Suppose concurrent write: • CRCW pi write data xi to location li, (li may be same for multiple pi ‘s). • Corresponding EREW pi write (li, xi) to a location A[i], (different A[i]’s) so exclusive write. • Sort all (li, xi)’s by li’s, same locations are brought together. in O(lg p). • Each EREW pi compares A[i]= (lj, xj), and A[i-1]= (lk, xk). If lj lk or i=0, then EREW pi writes xj to lj. (exclusive write). • See figure 30. 7. 19

20

CRCW vs. EREW • CRCW: – Some says: easier to program and more faster. – Others say: The hardware to CRCW is slower than EREW. And One can not find maximum in O(1). – Still others say: either EREW or CRCW is wrong. Processors must be connected by a network, and only be able to communicate with other via the network, so network should be part of the model. 21