Parallel Algorithms A parallel algorithm is an algorithm

Parallel Algorithms A parallel algorithm is an algorithm used to instruct more than one processors working together to solve a single problem.

SIMD‑SM model of parallel computation There are n identical processors, each of which can be identified by a processor number, i. e. an integer between 1 and n. All processors can perform typical operations such as arithmetic and Boolean operations independently. However, they are synchronized by a monitor to follow instructions of a unique instruction stream. All processors can simultaneously access a large common memory. However, different processors cannot read/write at the same memory location at the same time.

To indicate a parallel step in an algorithm for all processor i, lo<=i<=hi { …. }

A parallel step v. s. a loop for all processor i, 2<=i<=8 { a[i] = a[i]+a[i-1] } 1 2 3 4 5 6 7 8 a 1+a 2 a 2+a 3 a 3+a 4 a 4+a 5 a 5+a 6 a 6+a 7 a 7+a 8 for (i=2; i<=8; ++i) { a[i] = a[i]+a[i-1] } 1 2 3 4 5 6 7 8 a 1+a 2+a 3+a 4 a 1+a 2+a 3+a 4+a 5 a 1 ~ a 6 a 1 ~ a 7 a 1 ~ a 8

Speed up ratio Let T(n) be the time complexity of the best sequential algorithm for a certain problem. T(n)/p is the optimal time complexity can be achieved with p processors. T(n)/p * log 2 p is feasible and common.

Parallel Associative Fan‑In (p=n) Input: Array a[1. . n]. Output: sum = a[1]+a[2]+. . . +a[n]. d = 2; while (d<=n) { for all processor i, 1<=i<=n/d { a[d*i] = a[d*i]+a[d*i‑d/2]; } d = d*2; } sum = a[n];

Parallel Associative Fan-In (n=p) d=2 d=4 d=8 for all processor i, 1<=i<=n/d { a[d*i] = a[d*i]+a[d*i‑d/2]; }

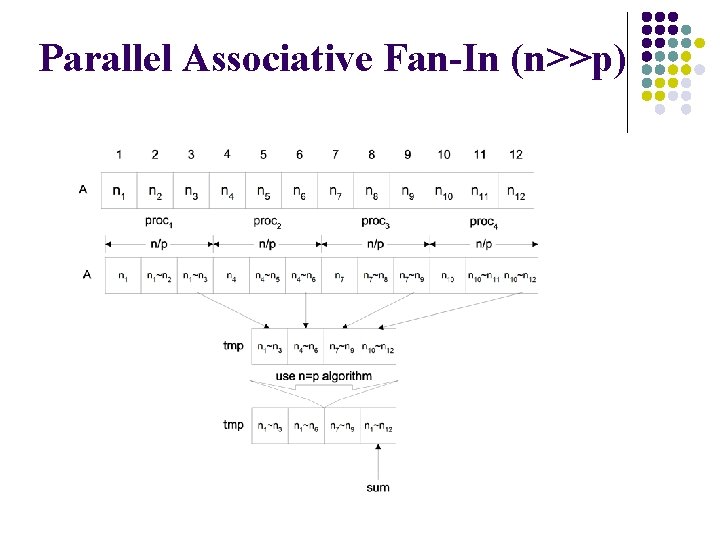
Parallel Associative Fan-In (n>>p) seg_size = n/p; for all processor i; 1<=i<=p; begin[i] = (i-1)*seg_size; for (j=2; j<=seg_size; ++j) { for all processor i; 1<=i<=p; a[begin[i]+j] += a[begin[i]+j-1]; } for all processor i; 1<=i<=p; s[i]= a[i*seg_size]; fan_in(s); sum = s[p];

Parallel Associative Fan-In (n>>p)

Parallel Partial_Sums (n=p) Input: Array a[1. . n]. Output: For all i, a[i] contains a[1]+a[2]+. . . +a[i]. d = 1; while (d<n) { for all processor i, d<i<=n { a[i] = a[i]+a[i‑d]; } d = d*2; }

Parallel Partial_Sums (n=p) d=1 d=2 d=4 for all processor i, d<i<=n { a[i] = a[i]+a[i‑d]; }

Parallel Partial_Sums (n>>p)

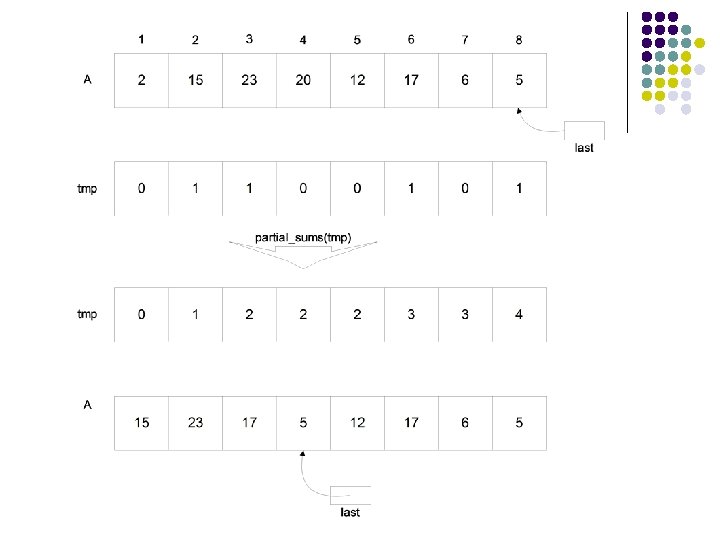
Parallel_Delete (n=p) Input: Array a[1. . n]. Output: For all 1<=i<=last, b[i] contains the i'th odd number of a. for all procesor i, 1<=i<=n { if (odd(a[i])) tmp[i] = 1; else tmp[i] = 0; } partial_sums(tmp); last = tmp[n]; for all procesor i, 1<=I<=n { if (odd(a[i])) a[tmp[i]] = a[i]; }

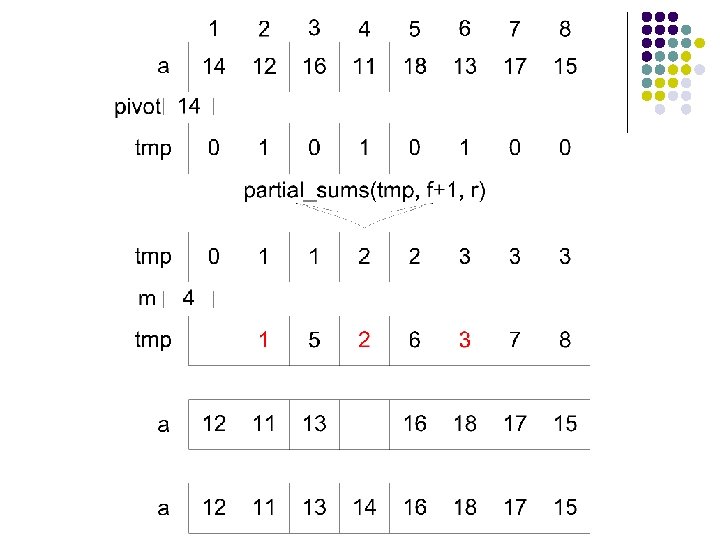
int parallel_partition(int f, int r) { /* Assume that a is a global array. */ pivot = a[f]; for all processor i, f<i<=r { if (a[i]<pivot) tmp[i] = 1; else tmp[i] = 0; } partial_sums(tmp, f+1, r); m = f+tmp[r]; /* Location for the pivot. */ for all processor i, f<i<=r { if (a[i]<pivot) tmp[i] = f‑ 1+tmp[i]; else tmp[i] = m+i‑f‑tmp[i]; a[tmp[i]] = a[i]; } a[m] = pivot; return m; }

Homework 1. Write the parallel partial sums algorithm for n>>p. 2. Assume that A[1. . n] is an array of numbers. a. Describe an efficient parallel algorithm that uses n processors to find the first local minimum of A. b. Describe an efficient parallel algorithm that uses p processors, where p << n, to find the first local minimum of A.