Paradigms in Autonomous Robotics Instructor Erol ahin Overview

Paradigms in Autonomous Robotics Instructor: Erol Şahin

Overview ¢ ¢ Control Architectures for Autonomous Robots Three paradigms § Hierarchical § Reactive/Behavior-based § Hybrid

Artificial Intelligence ¢ ¢ Beginnings of AI: Dartmouth Summer Research Conference (1955) Original topics studied: § § § ¢ Language Neural nets Complexity theory Self-improvement Abstractions Creativity Marvin Minsky: § an intelligent machine “would tend to build up within itself an abstract model of the environment in which it is placed. If it were given a problem it could first explore solutions within the internal abstract model of the environment and then attempt external experiments. ” Adapted from Lynne Parker’s slides

AI influence on Autonomous Robotics ¢ Through mid-80’s, AI research strongly dependent upon: § Representational knowledge § Deliberative reasoning methods § Hierarchical organization Adapted from Lynne Parker’s slides

Early robots - Shakey ¢ Shakey (SRI), 1960’s § One of first mobile robots § Sensors: Vidicon. TV camera § Optical range finder § Whisker bump sensors § § Environment: Office environment with specially colored and shaped objects § STRIPS planner: developed for this system Used world model to determine what actions robot should take to achieve goals Adapted from Lynne Parker’s slides §

Shakey video https: //www. youtube. com/watch? v=q. Xdn 6 ynwp

Shakey the robot ¢ 1970 -Shakey the robot reasons about its blocks Built at Stanford Research Institute, Shakey was remote controlled by a large computer. It hosted a clever reasoning program fed very selective spatial data, derived from weak edgebased processing of camera and laser range measurements. On a very good day it could formulate and execute, over a period of hours, plans involving moving from place to place and pushing blocks to achieve a goal. § From Hans Moravec Adapted from Jeremy Wyatt’s slides

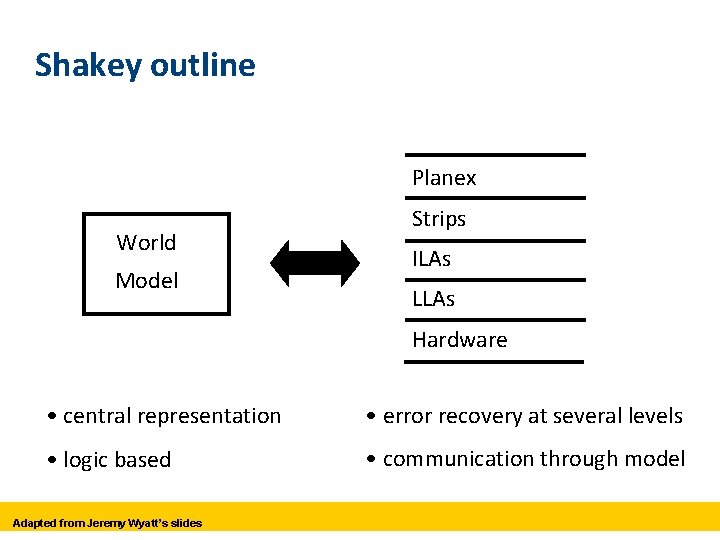
Shakey outline Planex World Model Strips ILAs LLAs Hardware • central representation • error recovery at several levels • logic based • communication through model Adapted from Jeremy Wyatt’s slides

STRIPS-Based Approach to Robot Control ¢ ¢ Use first-order logic and theorem proving to plan strategies from start state to goal STRIPS language: § “Classical” approach that most planners use § Lends itself to efficient planning algorithms § Retains expressiveness of situation calculus Adapted from Lynne Parker’s slides Shakey of SRI 1960’s

STRIPS Representation – States and Goals ¢ States: Conjunctions of function-free ground literals (i. e. , predicates applied to constant symbols, possibly negated) § Example: At(Home) Have(Milk) Have(Bananas) § Common assumption: If state description does not mention a given positive literal, then the literal is assumed to be false ¢ Goals: Conjunctions of literals, which can include variables § Example: At(x) Sells(x, Milk) § Assumption: variables are existentially quantified Adapted from Lynne Parker’s slides

STRIPS Representation -Actions ¢ STRIPS operators consist of: § Action description: name for what an agent does § Precondition: conjunction of positive literals (atoms) saying what must be true before operator can be applied § Effect: conjunction of literals (positive or negative) that describes how the situation changes when operator is applied § Organize effect as: – ADD LIST – DELETE LIST Adapted from Lynne Parker’s slides

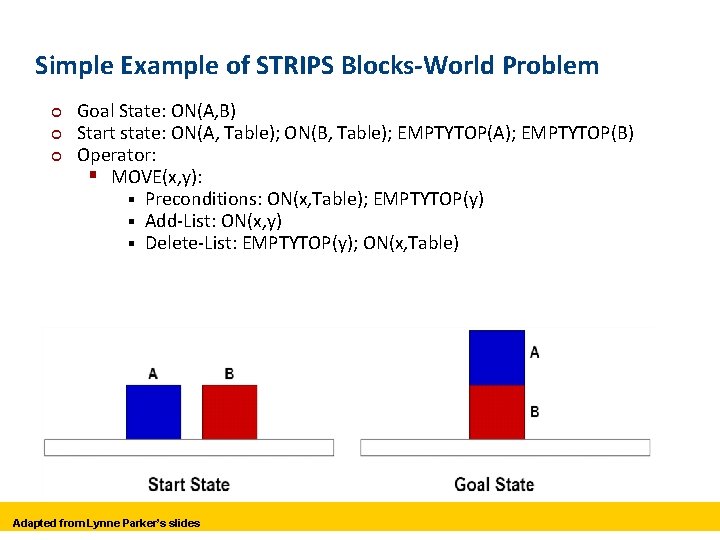
Simple Example of STRIPS Blocks-World Problem ¢ ¢ ¢ Goal State: ON(A, B) Start state: ON(A, Table); ON(B, Table); EMPTYTOP(A); EMPTYTOP(B) Operator: § MOVE(x, y): § Preconditions: ON(x, Table); EMPTYTOP(y) § Add-List: ON(x, y) § Delete-List: EMPTYTOP(y); ON(x, Table) Adapted from Lynne Parker’s slides

Shakey’s STRIPS World ¢ Types of actions Shakey can make (at least in simulation): § Move from place to place: § Go(y): – PRECOND: At(Shakey, x) » In(x, r) ∧In (y, r) » On(Shakey, Floor) – EFFECT: At(y) § Push movable objects: § Push(b, x, y): – PRECOND: Pushable(b) » At(b, x) » At(Shakey, x) » In(x, r) ∧ In (y, r) » On(Shakey, Floor) – EFFECT: At(b, y) Adapted from Lynne Parker’s slides

Shakey’s STRIPS World (con’t. ) ¢ Types of actions Shakey can make (at least in simulation): § Climb onto rigid objects: § Climb(b): – PRECOND: Climbable(b) » At(Shakey, x) ∧ At(b, x) » On(Shakey, Floor) – EFFECT: On(Shakey, b) § Climb down from rigid objects: § Turn light switches on and off: Adapted from Lynne Parker’s slides

After Shakey ¢ After twenty years the approach still didn’t extend § Visual modelling too hard and slow § Non-linear planning intractable (NP-complete) § Feedback through world model cumbersome Adapted from Jeremy Wyatt’s slides