Paradigms for Graph Drawing Algorithms for the Visualization

Paradigms for Graph Drawing: Algorithms for the Visualization of Graphs - Chapter 2 Presented by Liana Diesendruck

Graph Drawing Methods: Parameters Input: graph G – E(G) and V(G) Additional input: class of G - like: planar, directed acyclic, tree, etc. Specific algorithms work better for specific type of graphs Highlight a particular graph characteristic

Graph Drawing Methods: Concepts Drawing convention – ( אמנה basic rule that the drawing must satisfy to be admissible) Aesthetics - אסתטיקה Constraints - אילוצים

Graph Drawing Methods: Concepts Drawing conventions: Polyline drawing Straight-line drawing Orthogonal drawing Grid drawing Planar drawing Upward drawing

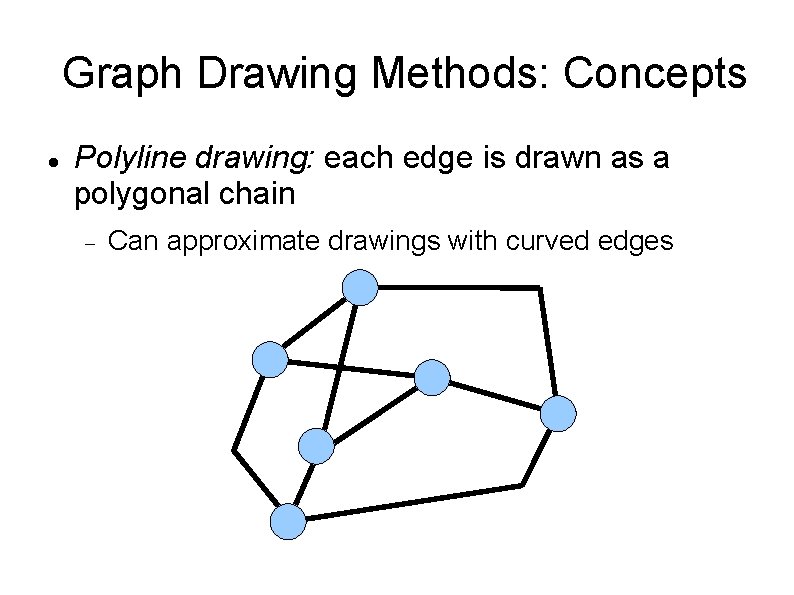
Graph Drawing Methods: Concepts Polyline drawing: each edge is drawn as a polygonal chain Can approximate drawings with curved edges

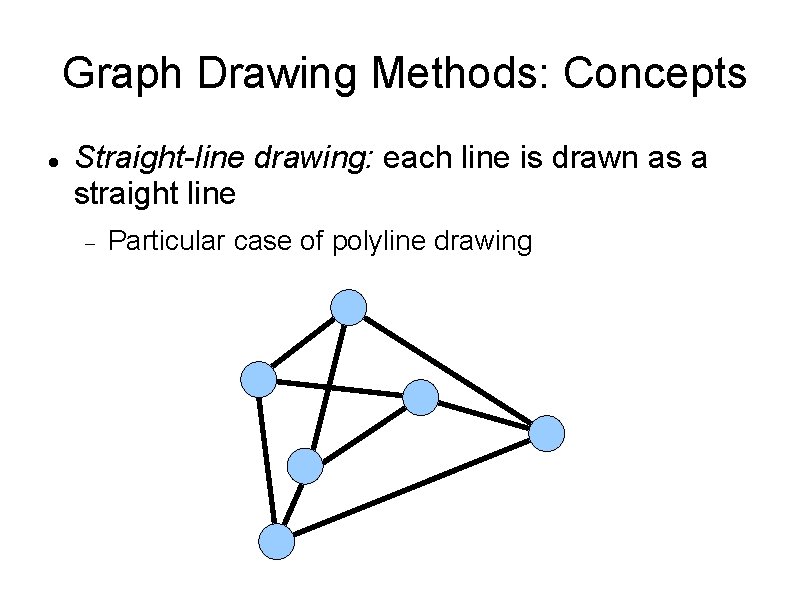
Graph Drawing Methods: Concepts Straight-line drawing: each line is drawn as a straight line Particular case of polyline drawing

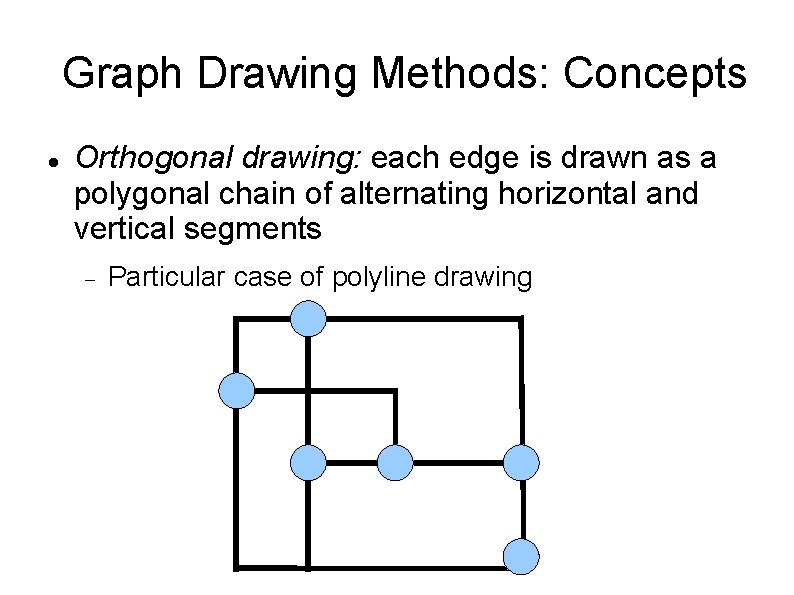
Graph Drawing Methods: Concepts Orthogonal drawing: each edge is drawn as a polygonal chain of alternating horizontal and vertical segments Particular case of polyline drawing

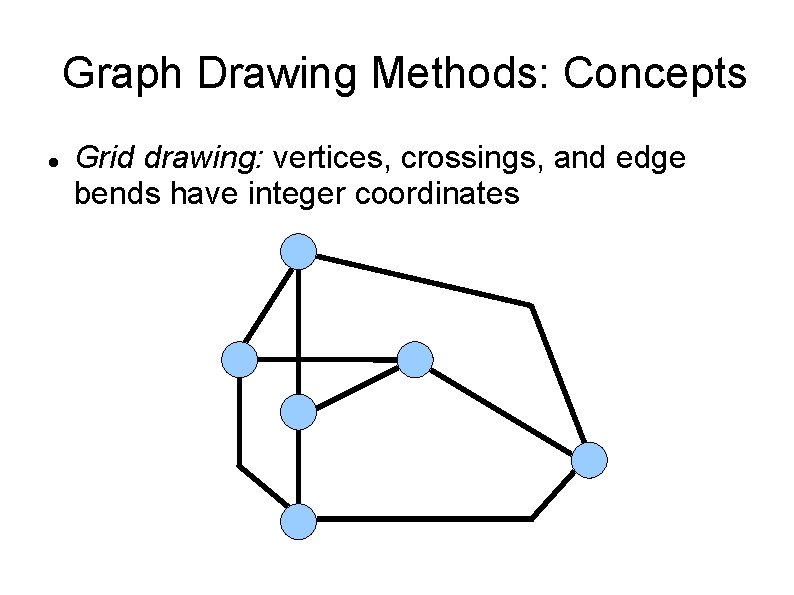
Graph Drawing Methods: Concepts Grid drawing: vertices, crossings, and edge bends have integer coordinates

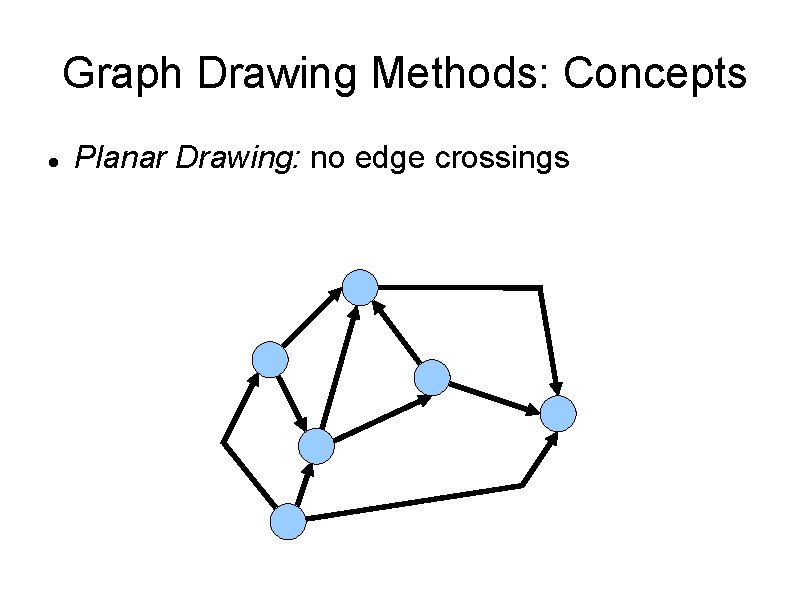
Graph Drawing Methods: Concepts Planar Drawing: no edge crossings

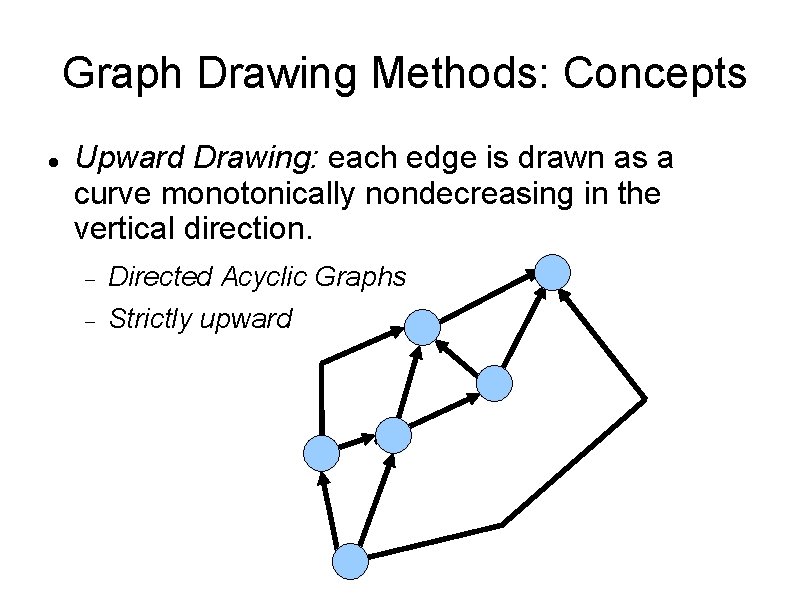
Graph Drawing Methods: Concepts Upward Drawing: each edge is drawn as a curve monotonically nondecreasing in the vertical direction. Directed Acyclic Graphs Strictly upward

Graph Drawing Methods: Concepts Aesthetics: specify graphic properties we would want to apply as much as possible to achieve readability. Crossings Area Total / Maximum / Uniform Edge Length Total / Maximum / Uniform Bends Angular resolution Aspect Ratio Symmetry

Graph Drawing Methods: Concepts Crossings: minimization of the total number of crossings. Ideally we would have planar graphs (not always possible).

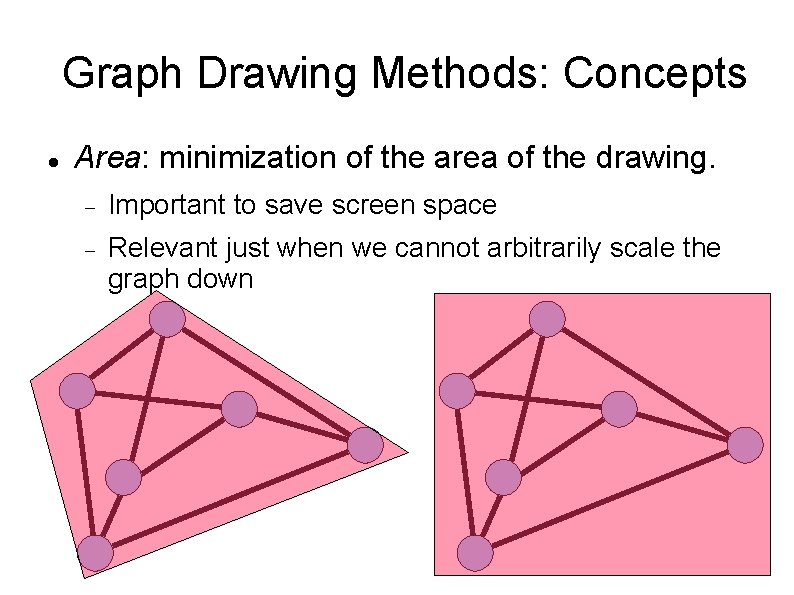
Graph Drawing Methods: Concepts Area: minimization of the area of the drawing. Important to save screen space Relevant just when we cannot arbitrarily scale the graph down

Graph Drawing Methods: Concepts Total Edge Length: minimization of the sum of the lengths of the edges. Maximum Edge Length: minimization of the maximum length of an edge. Both relevant just when we cannot arbitrarily scale the graph down. Uniform Edge Length: minimization of the variance of the lengths of the edges.

Graph Drawing Methods: Concepts Total Bends: minimization of the total number of bends along the edges. Important for orthogonal drawings Trivially satisfied by straight-line drawings Maximum Bends: minimization of the maximum number of bends on an edge. Uniform Bends: minimization of variance of the number of bends on an edge.

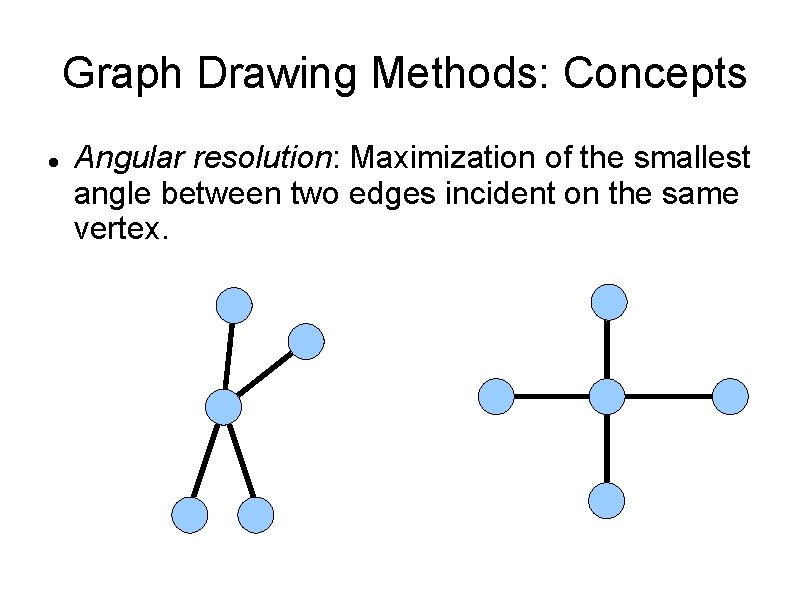
Graph Drawing Methods: Concepts Angular resolution: Maximization of the smallest angle between two edges incident on the same vertex.

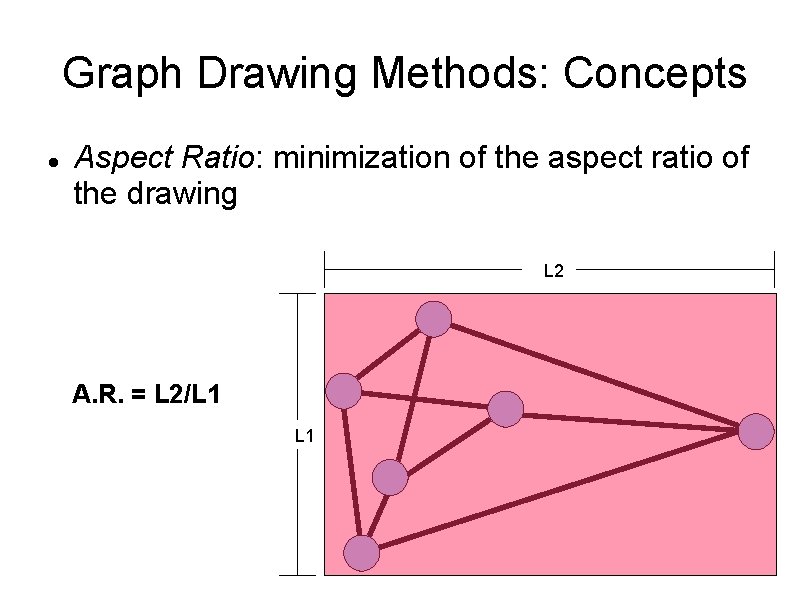
Graph Drawing Methods: Concepts Aspect Ratio: minimization of the aspect ratio of the drawing L 2 A. R. = L 2/L 1

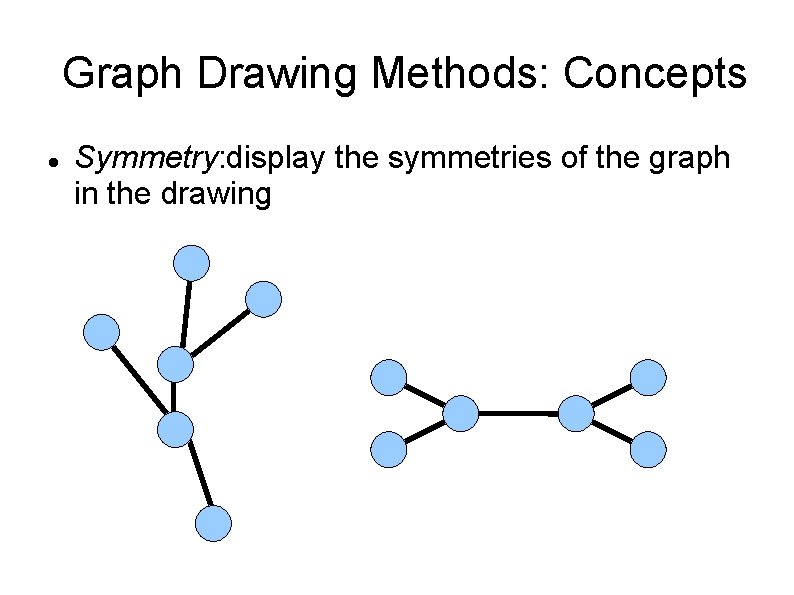
Graph Drawing Methods: Concepts Symmetry: display the symmetries of the graph in the drawing

Graph Drawing Methods: Concepts Most aesthetics are associated with optimization problems – most of them computationally hard. Approximation strategies and heuristics for realtime response.

Graph Drawing Methods: Concepts Constraints: refer to specific subgraphs and subdrawings. Commonly used in visualization applications. Usually include: Center: place a given vertex close to the center of the drawing External: place a given vertex on the outer boundary of the drawing Cluster: place a subset of vertices close together Left-right sequence: draw a given path horizontally aligned from the left to the right Shape: draw a given subgraph with a predefined “shape”

Precedence Among Aesthetics Most drawing techniques are based in the following two observations: Aesthetics often conflict with each other Even if they don't, it is often difficult to deal with all of them at the same time

Precedence Among Aesthetics Graph drawing methodologies established a precedence among aesthetics. Such precedence is more suitable for certain applications than for others. The common approaches to graph drawings usually divide the process into a sequence of steps. Each step is targeted to satisfy a certain subclass of aesthetics.

Topology-Shape-Metrics Approach Suited for orthogonal grid drawings Topology: two orthogonal drawings have the same topology if one can be obtained from the other by deformation that doesn't alter the sequence of edges contouring the faces of the drawing

Topology-Shape-Metrics Approach Shape: two orthogonal drawings have the same shape if one can be obtained from the other by modifying the lengths of the segments of the edges without changing their angles Metrics: two orthogonal drawings have the same metrics if they are congruent, up to a translation and/or rotation

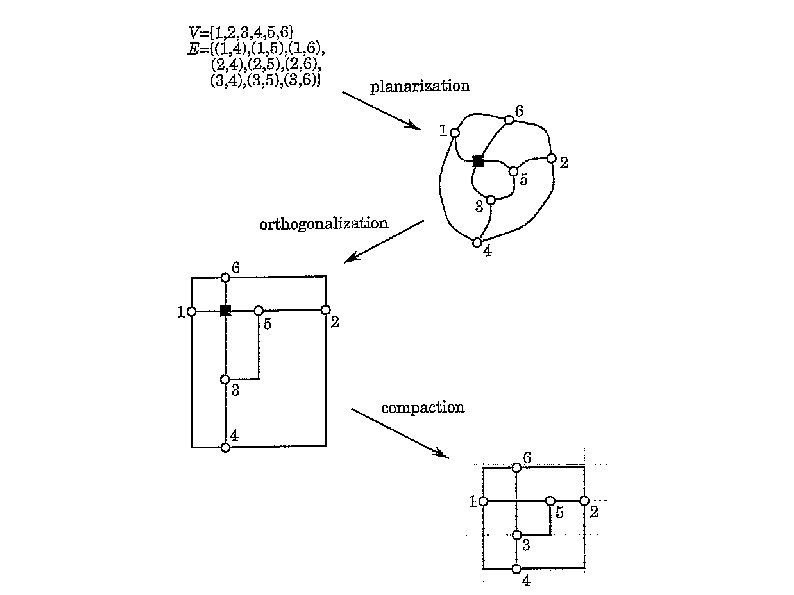
Topology-Shape-Metrics Approach The approach has 3 steps: Planarization Orthogonalization Compaction

Topology-Shape-Metrics Approach Planarization (determines the topology) Try to reduce the number of edge crossings as much as possible Possible algorithm: Extract the maximal planar subgraph of the given graph Insert the “non-planar” edges one by one, minimizing the number of crossings caused at each insertion Represent each crossing by a dummy vertex, so the final topology is planar

Topology-Shape-Metrics Approach Orthogonalization (determines the shape) Outputs the orthogonal representation of the graph. Each edge (u, v) is equipped with a list of angles, that describes the bends that the orthogonal line representing (u, v) will have in the final drawing

Topology-Shape-Metrics Approach Compaction (determines the metrics) Determines the final coordinates of the vertices and of the edge bends Try to minimize the drawing area Dummy vertices are removed Constraints: Topological – edge crossings, fix a vertex in the external face of the drawing, etc. Shape – require that a given path doesn't have bends Metrics – constrain the relation between vertices coordinates

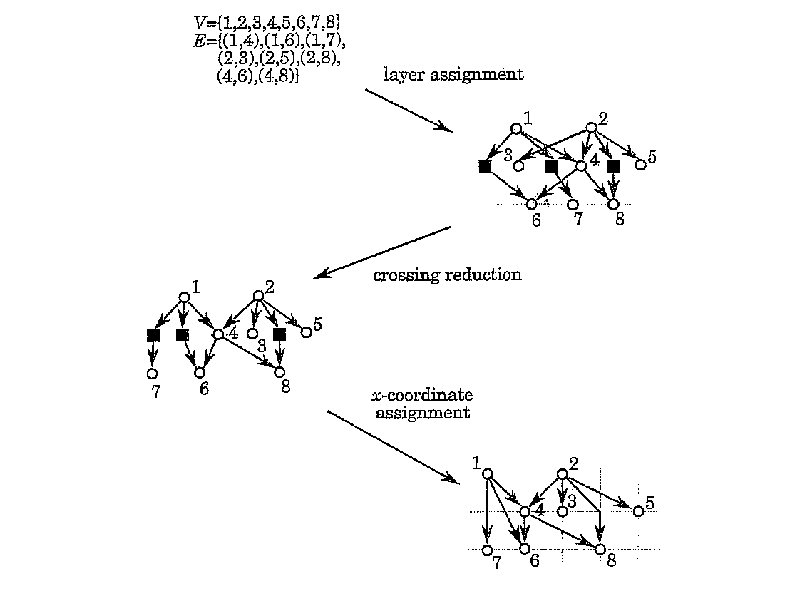
Hierarchical Approach Suited for directed graphs, particularly for acyclic directed graphs with the polyline downward drawing convention. Steps: Layer assignment Crossing reduction X-coordinate assignment

Hierarchical Approach Layer assignment: Produce a layered directed graph with layers and , then i > j Produce a proper layered directed graph If (u, v) is an edge where and , then i = j+1 Do it by inserting dummy vertices along edges that span more than two layers Assign y=i to every vertex in

Hierarchical Approach Crossing reduction: Receive the proper layered graph Order the vertices on each layer, so to minimize the amount of edge crossings X-coordinate assignment: Preserve the order received on each layer Assign x-coordinates to every vertex Represent each edge by a straight line Remove dummy vertices

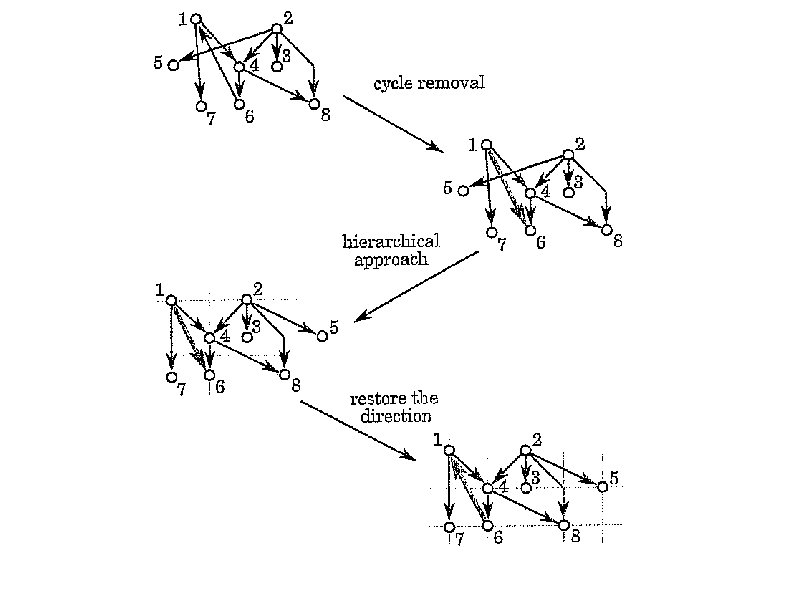
Hierarchical Approach Can also be used in graphs that are not acyclic: Cannot preserve the downward convention, but can minimize the amount of upward edges First, force the graph to be acyclic by reversing a subset of edges (as small as possible) Then apply the hierarchical approach Finally, restore the original direction of the reversed edges

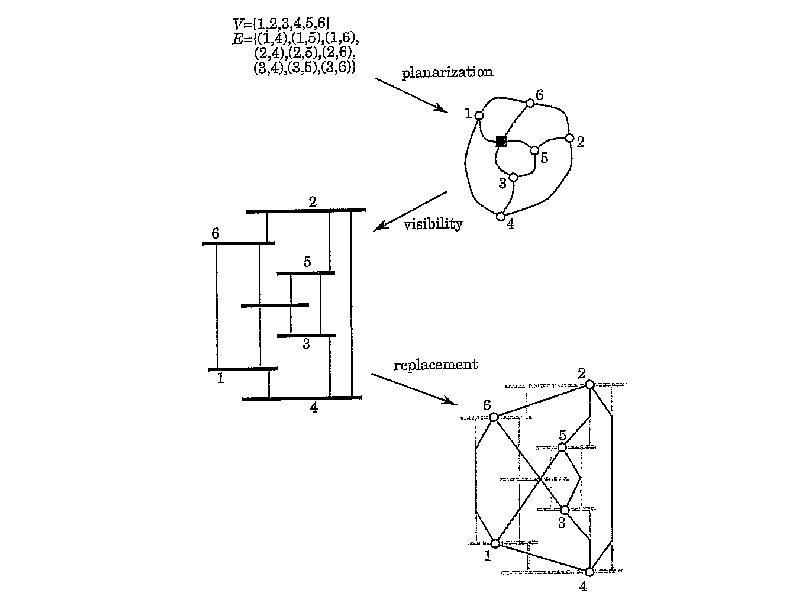
Visibility Approach Suited for drawing graphs with the polyline drawing convention Steps: Planarization (as in the topology-shape-metrics approach) Visibility Replacement

Visibility Approach Visibility: Construct a visibility representation of the graph: Map each vertex to a horizontal segment Map each edge to a vertical segment s. t. , the vertical segment (u, v) has endpoints on the horizontal segments representing u and v and does not intersect with any other horizontal segment

Visibility Approach Replacement: Construct the final polyline: Replace each horizontal segment by a point Replace each vertical segment by a polygonal line, following the original vertical assignment

Visibility Approach Planarization step as in the topology-shapemetrics approach Visibility step similar to layer assignment in the hierarchical approach So, it can be considered as a meeting point of the topology-shape-metrics and the hierarchical approaches Aesthetic considerations and general constraints can be added to suitable steps

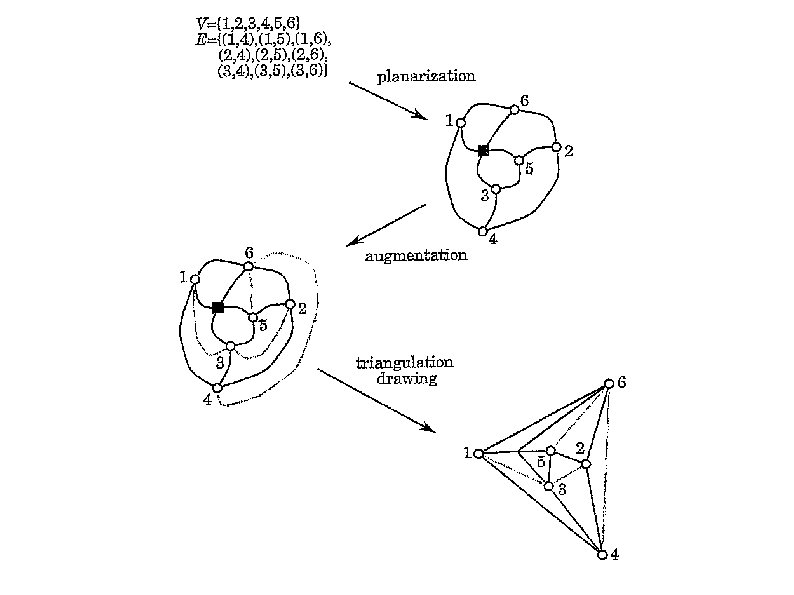
Augmentation Approach Also suited for the polyline drawing convention Basic idea: add edges and/or vertices to the graph to obtain a new graph with a stronger structure and better drawability properties Steps: Planarization (as in the topology-shape-metrics approach) Augmentation Triangulation drawing

Augmentation Approach Augmentation: Add a set of edges (sometimes also vertices) to the planar embedding s. t. a maximal planar graph is obtained (planar graph whose faces have three edges) Try to keep the degrees of the vertices as small as possible

Augmentation Approach Triangulation drawing: Represent each face as a triangle Remove dummy edges and vertices Can use strategies to minimize the graph area, maximize angular resolution and uniform distribution of vertices

Augmentation Approach If the graph is planar, then the result drawing is straight-line. Otherwise, the dummy vertices become bends. This approach is less suitable than others for supporting constraints.

Force-directed Approach Good for creating straight-line drawings of undirected graphs Popular mostly because it is easy to understand code Simulates a system of forces over the input graph and outputs a locally minimum energy configuration Two ingredients: Force model Locally minimum configuration finding technique

Force-directed Approach Example of a force model: Locally minimum configuration finding technique: Each pair (u, v) is assigned with a spring with length luv that is the number of edges on the shortest path between u and v. The spring follows Hooke's law. Usually by numerical analysis (simple iterative methods) Tends to give highly symmetric drawings and distribute vertices evenly Constrains can be added by special forces

Divide and Conquer Approach Suited for graphs that can be easily decomposed into subgraphs, such as trees. Main idea: split the graph into subgraphs; recursively draw the subgraphs; the drawing of the whole graph is obtained by gluing the drawings of the subgraphs.

Divide and Conquer Approach Example: algorithm for drawing binary trees in 2 main steps: Layer assignment (as in the hierarchical approach), trying to minimize the distance from the root Divide and Conquer: If the tree is a single vertex, then trivially construct its drawing on the assigned layer. If the tree is empty, do nothing. Else, (divide) recursively divide the left and right subtrees and (conquer) place the two subdrawings obtained close to one another with the root positioned halfway between the roots of the subtrees.

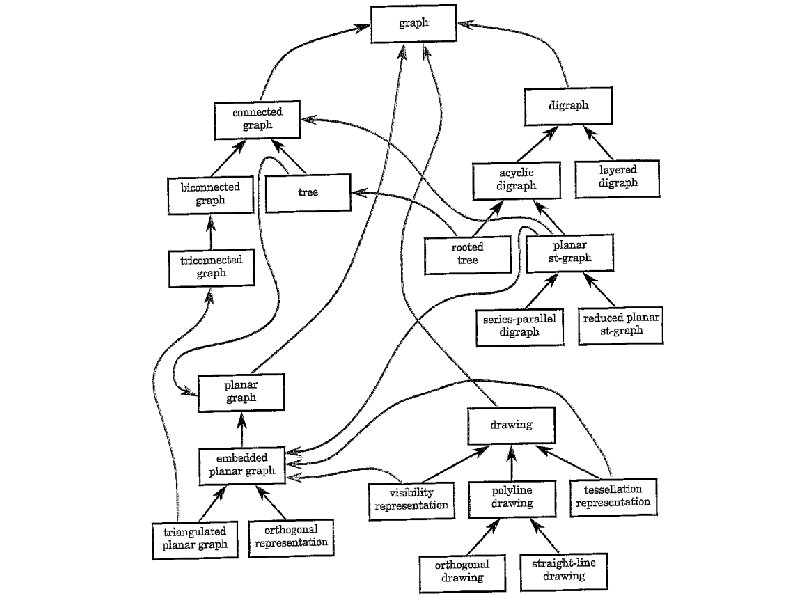
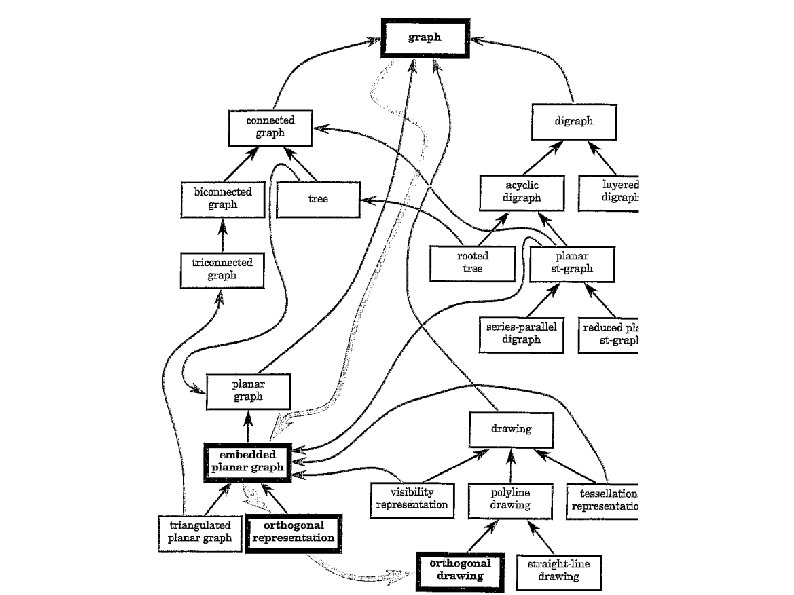
General Framework for Graph Drawing Let C be a class of graphs and let C' be a subclass of C. If an algorithm can be applied tp the graphs of C, it can also be applied to the graphs of C'. That is, C' inherits the algorithms for C. Graph drawing methodology is composed of a series of relatively independent functional steps. Where the inputs and outputs are always graphs.

General Framework for Graph Drawing Inheritance hierarchy of classes of graphs Set of methods with the following characteristics: Each method is associated with a class of graphs and maps a graph of that class into a graph of another class A method associated with a class of graphs C is also associated with all the descendant classes of C in the hierarchy.

General Framework for Graph Drawing The most general class in the hierarchy is Graph According to certain properties, the subclasses of Graph are: Connected Graphs Planar Graphs Directed Graphs Drawing

Summary Drawing conventions Aesthetics Constraints Precedence among aesthetics 6 different approaches to graph drawing Hierarchy and inheritance