ParaCORDIC Parallel CORDIC Rotation Algorithm and Architecture IEEE

Para-CORDIC: Parallel CORDIC Rotation Algorithm and Architecture (IEEE T-CAS I, Vol. 51, No. 8, pp. 1515 -1524, Aug. 2004) Tso-Bing Juang, Ph. D VLSI Design LAB, Dept. CSE, NSYSU tsobing@cse. nsysu. edu. tw 1

My Research – Computer Arithmetic p Applications of arithmetic components n n n p DSP (Digital Signal Processing) 3 -D graphics Computer communications, etc. Topics of arithmetic [Ercegovac 2004]: n n Addition/Subtraction Multiplication/Division Floating-point operations CORDIC (COordinate Rotation DIgital Computer) 2

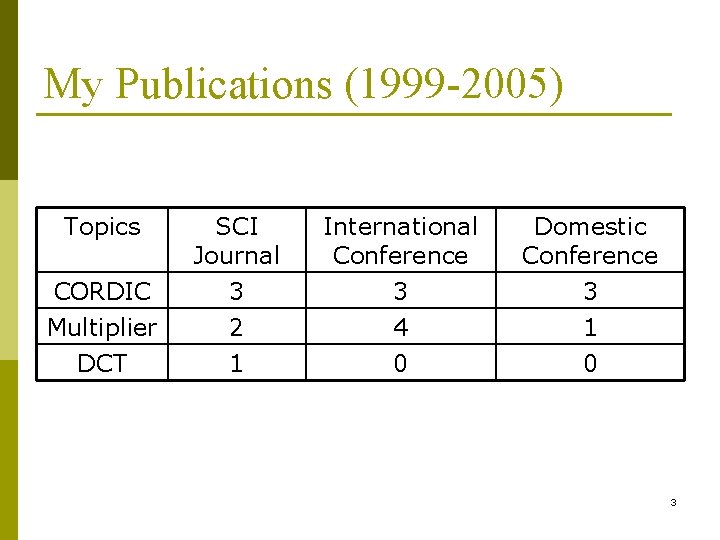
My Publications (1999 -2005) Topics SCI Journal International Conference Domestic Conference CORDIC Multiplier DCT 3 2 1 3 4 0 3 1 0 3

Academic Honors p Best thesis award, Xerox Co. Ltd, 1995 p Join Midwest Symposium of Circuits and Systems (MWSCAS) supported by NSC, 1999 p First prize award of FPGA, National Intellectual Property Contest. FPGA, 2000 p First prize award of Full Custom Design Contest, 2001 p Join Asia-Pacific Conference on Circuits and Systems (APCCAS) supported by MOE, 2002 p 2005 Marquis, Who’s who in Science and Engineering, Edition 2005 -2006 p 2006 Marquis, Who’s who in the World 4

Outline Basic Concept of CORDIC p Bottleneck of CORDIC Rotation p Proposed Methods p Previous Methods p Comparisons p Applications p Conclusions p 5

1. Basic Concept of CORDIC 6

What is CORDIC? p CORDIC (COordinate Rotation DIgital Computer) n Rotate vector (1, 0) by f to get (cos f, sin f) n Can evaluate many arithmetic functions n Rotation realized by shift-add operations n Convergence method (iterative) p About n iterations for n-bit accuracy 7

Conventional CORDIC Rotation . Each iteration, x and y performs one micro-rotation based on the sign of z 8

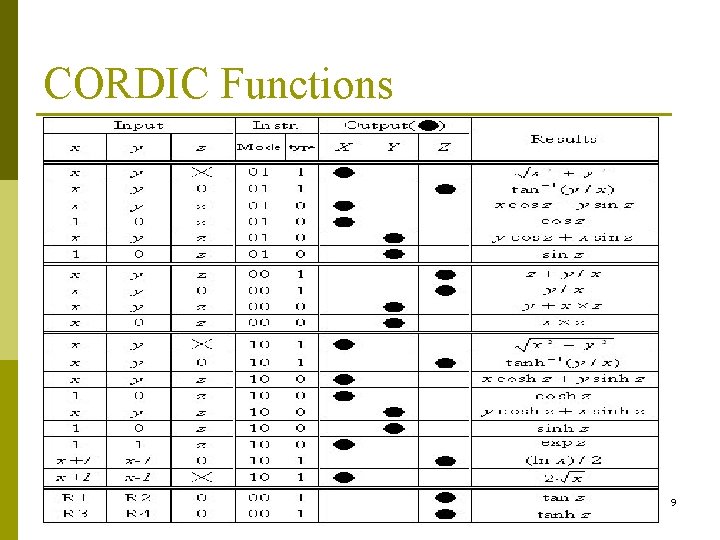
CORDIC Functions 9

Pre-computation of tan(ai) p p Find ai such that tan(ai)=2 -i (or, ai=tan-1(2 -i)) Possible to write any angle f = a 0 a 1 … an as long as -99. 7° f 99. 7° (which covers – 90. . 90) 10

Conventional CORDIC Rotation p Algorithm: (z is the current angle) n “At each step, try to make z approach to zero” n Initialize x 0=K=0. 607253, y 0=0, z 0= n For i = 0 n n i= 1 when zi>=0, else -1 [i. e. , i=sign(zi)] p p p n xi+1 = xi – i 2 -i yi yi+1 = yi + i 2 -ixi zi+1 = zi – i ai End For Result: xn+1=cos( ), yn+1=sin( ) n Precision: n bits n 11

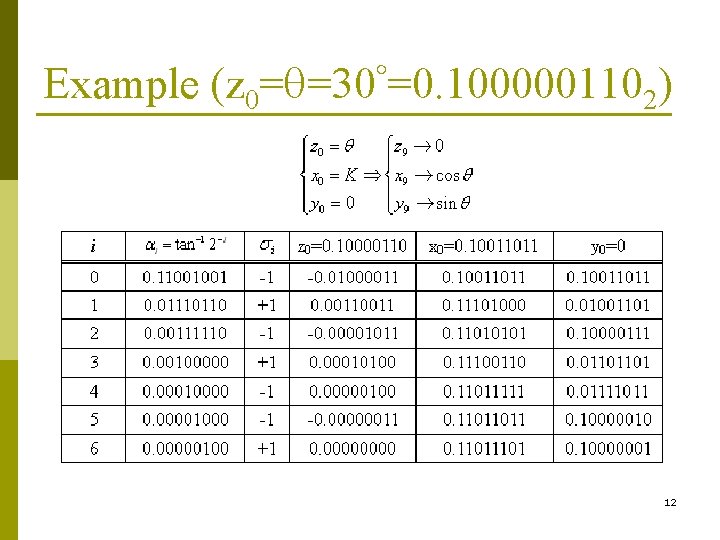
Example (z 0= =30 =0. 1000001102) 12

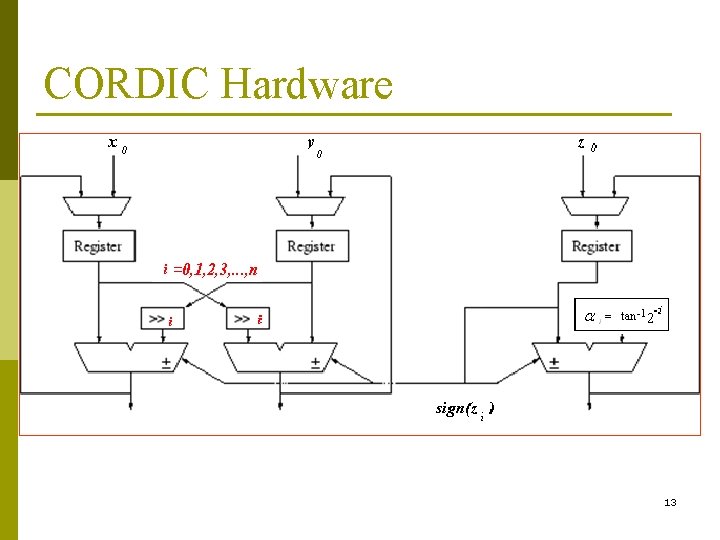
CORDIC Hardware 13

Three Important Factors of CORDIC p Large additions/subtractions p Scaling factor (constant vs. non-constant) p Sequential execution 14

Research Topics about CORDIC Redundant CORDIC architecture p Error analysis of CORDIC p Application of CORDIC architectures p CORDIC algorithm with non-constant scaling factors p Parallel CORDIC architecture p 15

2. Bottleneck of CORDIC Rotation 16

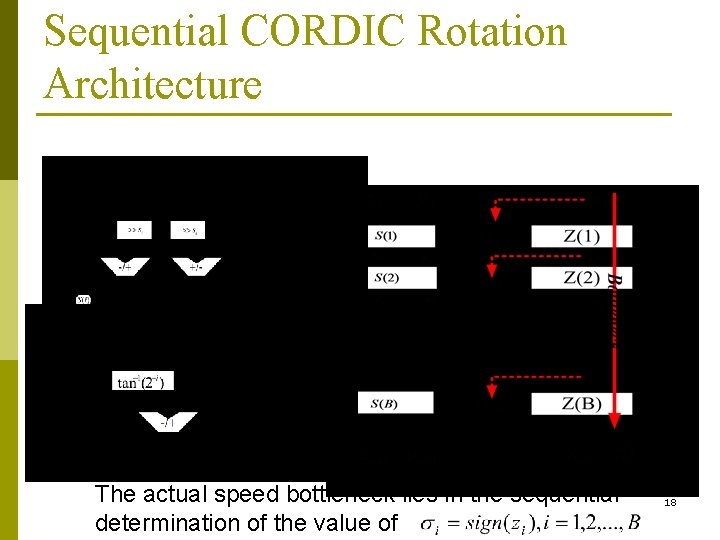
Conventional CORDIC Rotation (Revisited) . Sequential determination of σi based on zi 17

Sequential CORDIC Rotation Architecture The actual speed bottleneck lies in the sequential determination of the value of 18

3. Proposed Methods 19

How to parallelize? p p Using each bit of input angle to determine σi Remove the bottleneck (B: bit accuracy) n In the first m-1 iterations sequential n In other iterations parallel 20

Our Proposed Techniques p MAR (Micro-rotation to Angle Recoding) n Obtain the combinations of tan-1 terms in each 2 -i, i=1 to m-1 For example, B=24 p BBR (Binary to Bipolar Recoding) n Obtain the polarity{-1, +1} of each binary {1, 0} weight of input angle hardware free 21

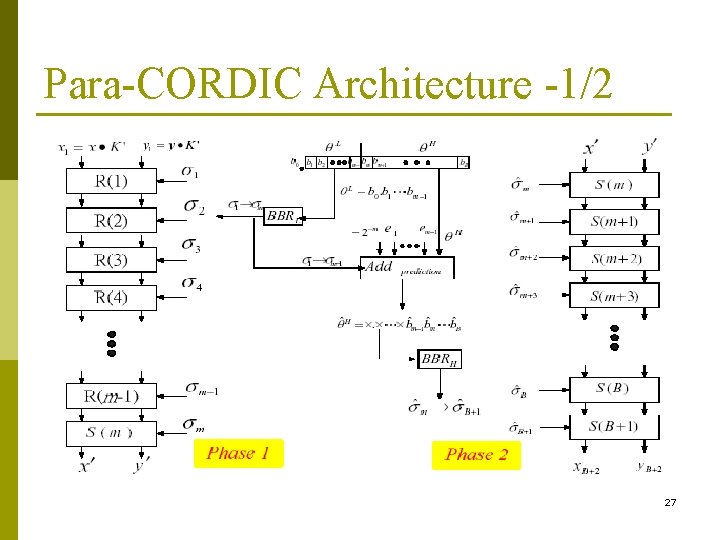
Example (B=24) Phase 1 Three extra micro-rotation stages are required Phase 2 22

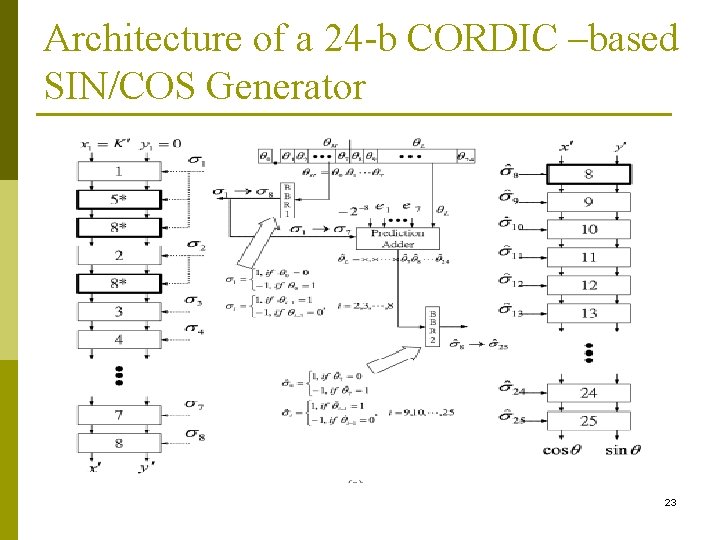
Architecture of a 24 -b CORDIC –based SIN/COS Generator 23

Algorithm of MAR 24

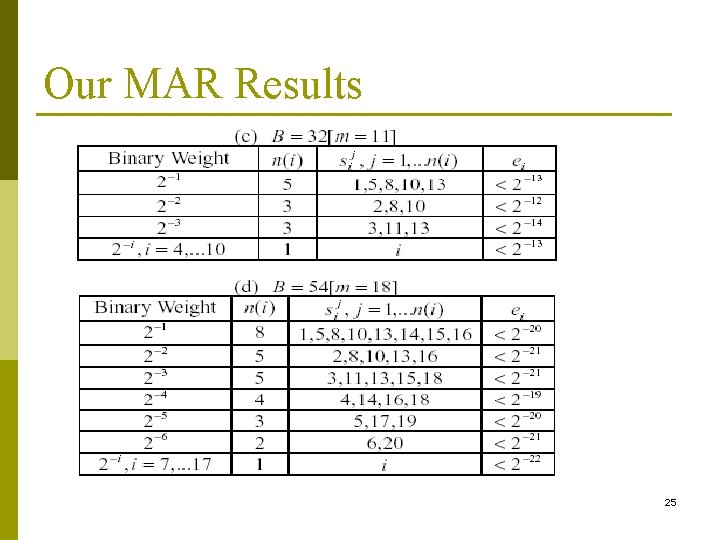
Our MAR Results 25

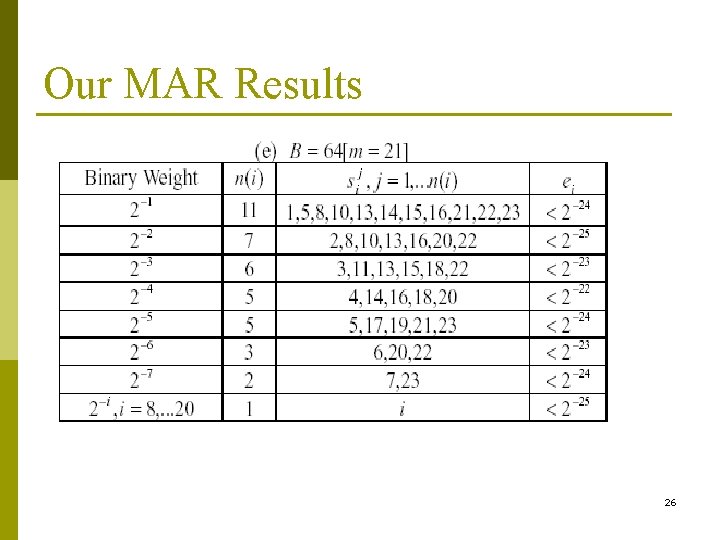
Our MAR Results 26

Para-CORDIC Architecture -1/2 27

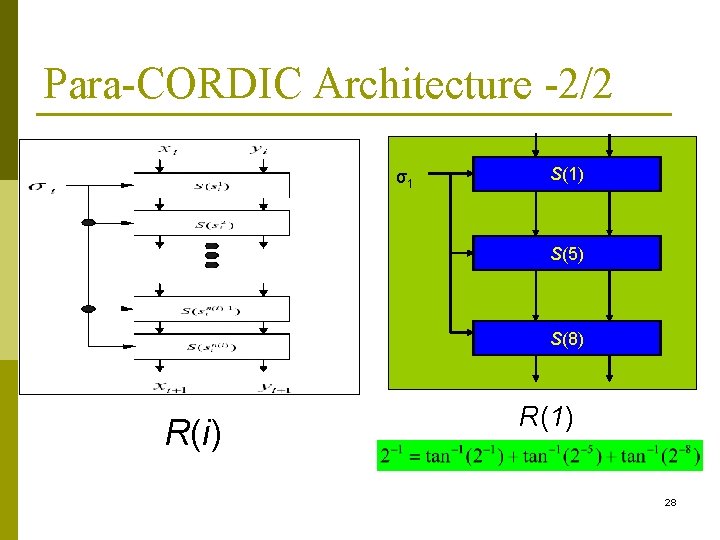
Para-CORDIC Architecture -2/2 σ1 S(1) S(5) S(8) R(i) R(1) 28

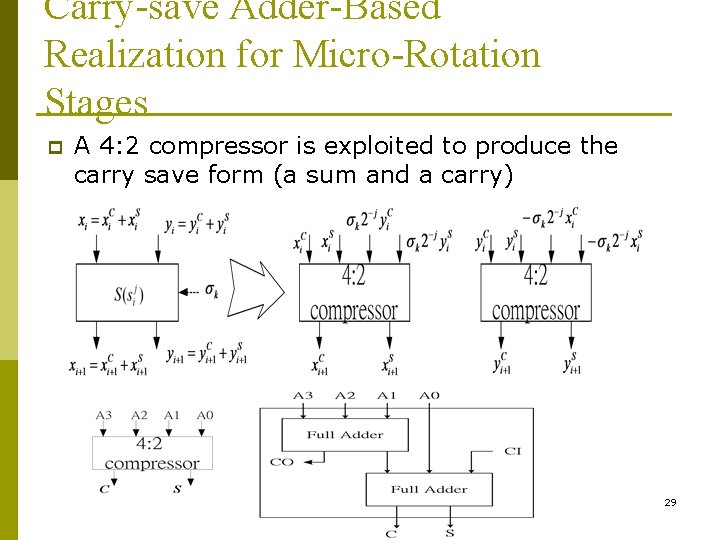
Carry-save Adder-Based Realization for Micro-Rotation Stages p A 4: 2 compressor is exploited to produce the carry save form (a sum and a carry) 29

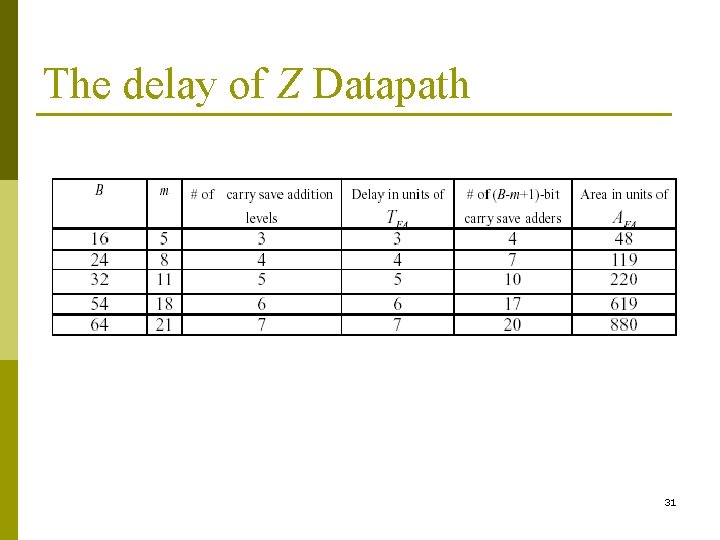
Evaluation of the Z Datapath p Delay is: p Area is: 30

The delay of Z Datapath 31

Merged Rotations of the Second Half Iterations p Delay savings 32

4. Previous Methods 33

Comments of Previous Proposed CORDIC Rotation – 1/4 p [Wang 1997]: IEEE T-Computers n n The first m-1 iterations are sequential Area saving 34

Comments of Previous Proposed CORDIC Rotation - 2/4 p [Phatak 1998]: IEEE T-Computers n n Double hardware to perform clockwise/counterclockwise rotations Area cost is high (signed-digit realization of X/Y/Z iterations) 35

Comments of Previous Proposed CORDIC Rotation - 3/4 p [Kwak 2000] Proc. MWSCAS n Complicated logic circuits to generate the first m-1 rotation directions 36

Comments of Previous Proposed CORDIC Rotation - 4/4 p [Kuhlmann 2002] : EUROSIP n Using ROM to generate the first m-1 directions 37

Our Proposed Para-CORDIC p The delay and the area costs of para. CORDIC is: and 38

5. Comparisons 39

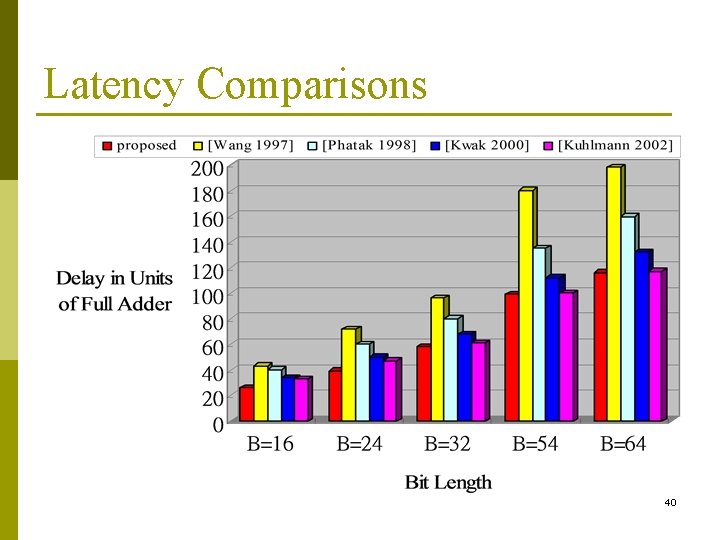
Latency Comparisons 40

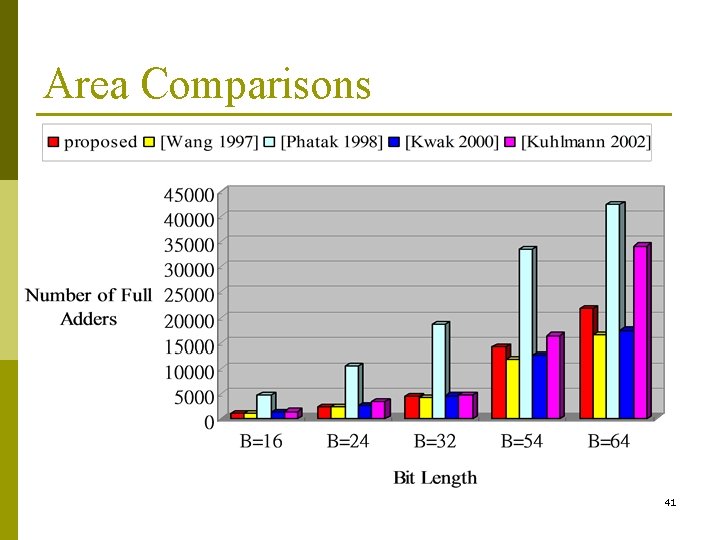
Area Comparisons 41

6. Applications 42

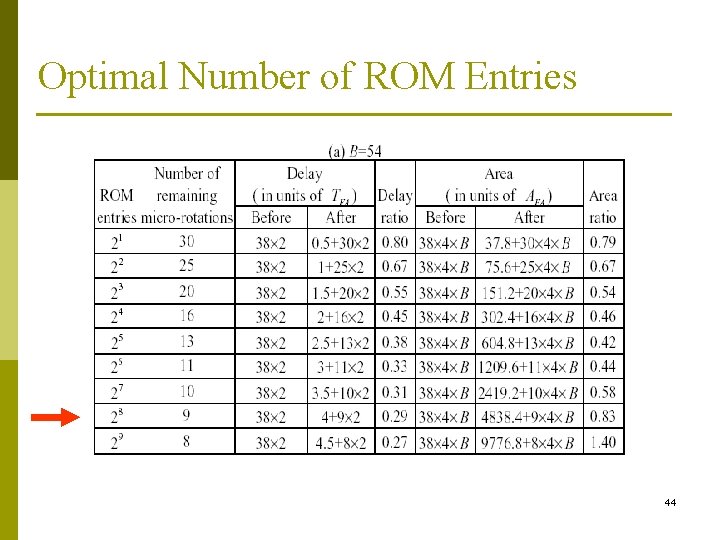
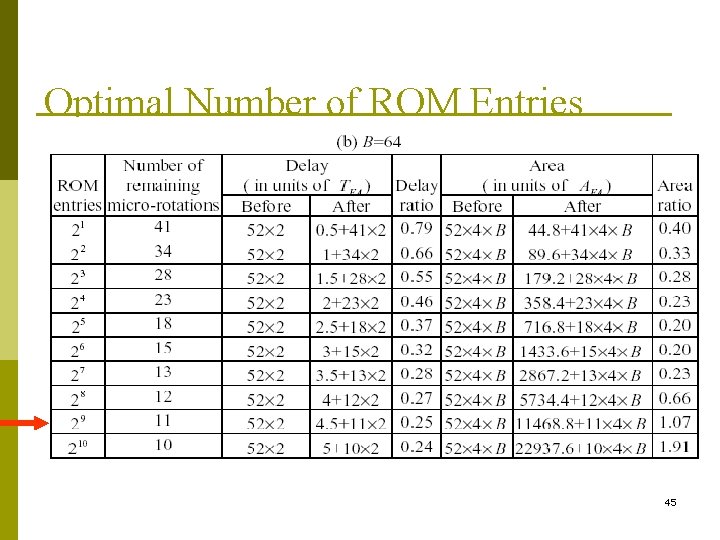
ROM-based Implementations for sine/cosine generation p When x 1 and y 1 are constant (x 1=K, y 1=0, p Can reduce the extra micro-rotation stages x. B+1=cos( ), y. B+1=sin( )) 43

Optimal Number of ROM Entries 44

Optimal Number of ROM Entries 45

7. Conclusions 46

Summary p Parallel CORDIC rotation (Para-CORDIC) n n n Improve the original sequential execution of CORDIC rotation Complete proof of the proposed theorems Submission information 2003/7/11 submitted p 2004/4/21 fully accepted p 2004/8 published p p Better latency/area 47

Future Work p Physical implementation of Para-CORDIC n n n p Dealing with the negative numbers when perform carry-save addition Floating-point representation of data Reduced micro-rotation stages in MAR Parallel CORDIC Vectoring Methods n Must deal with two concurrent variables 48

Low-Error Fixed-Width Carry-Free Multipliers Design ( To appear in IEEE T-CAS II, 2005) 49

Definition p An n n fixed-width multiplier n Has n most significant product bits n Needs a small compensation circuit to generate error compensation value (ECV) p ECV n Constant p p n Fixed Simplementation, large errors Adaptive p p Variable Complex implementation, lower errors 50

An 8 8 Carry-Free Fixed-Width Multiplier using Modified Booth Encoding (MBE) LPminor = others in truncated parts Mpost = truncates the bit after multiplication 51

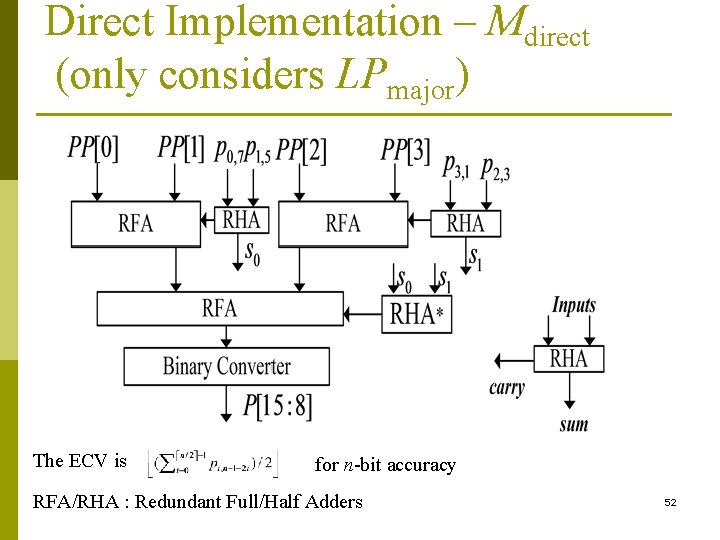
Direct Implementation – Mdirect (only considers LPmajor) The ECV is for n-bit accuracy RFA/RHA : Redundant Full/Half Adders 52

The Concept of Our Derivation of Compensation Circuits p Using the basic definition of MBE to obtain the possibility of each partial product digit equals to 1, -1 and 0. n p Previous works: same probability of each partial product Using statistical analysis to derive the relationship between LPminor and LPmajor n Previous works: only makes use of LPmajor 53

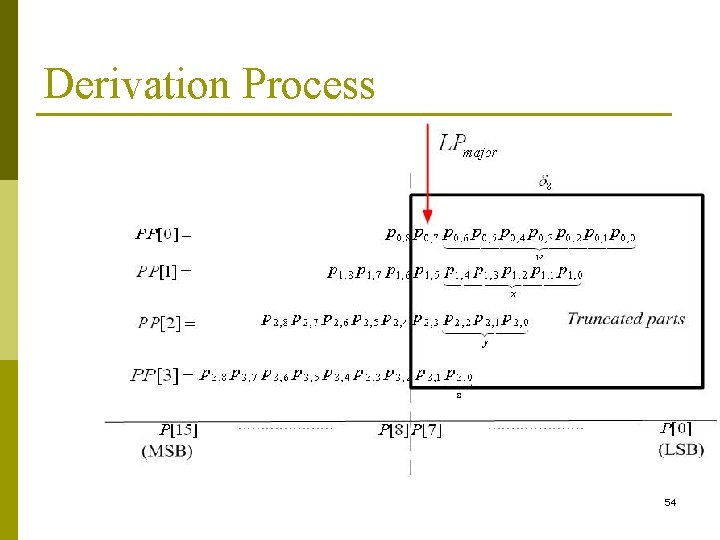
Derivation Process 54

Derivation of Compensation Value and Circuit 55

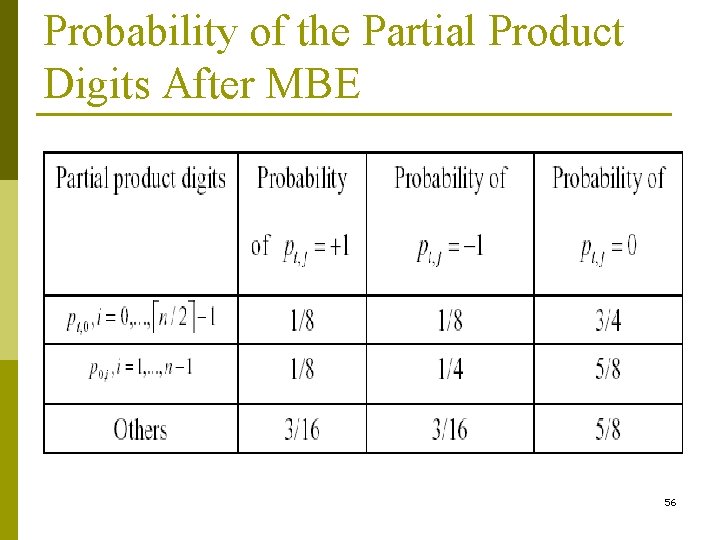
Probability of the Partial Product Digits After MBE 56

Derivation of Compensation Value and Circuit p The expected value can be derived by considering three conditions when p (1) 57

Derivation of Compensation Value and Circuit p (2) 58

Derivation of Compensation Value and Circuit p (3) 59

Derivation of Compensation Value and Circuit p Combining (1)(2)(3), p Using similar methods, we have 60

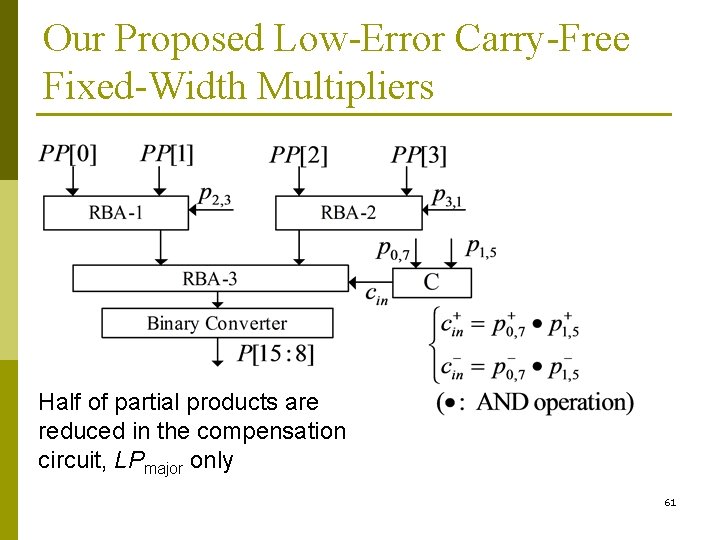
Our Proposed Low-Error Carry-Free Fixed-Width Multipliers Half of partial products are reduced in the compensation circuit, LPmajor only 61

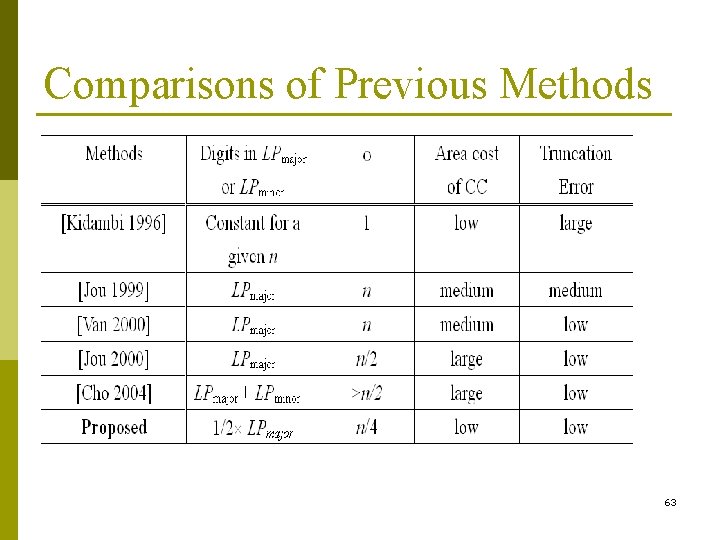
Previous Proposed Fixed-Width Multipliers p All are binary representations n [Kidambi 1996]: the ECV is a pre-determined constant n [Jou 1999]: LPmajor to generate ECV. n [Van 2000]: program-based exhaustive search method to obtain ECV n [Jou 2000]: MBE, similar to the direct implementation n [Cho 2004]: LPmajor and LPminor are required to calculate the ECV 62

Comparisons of Previous Methods 63

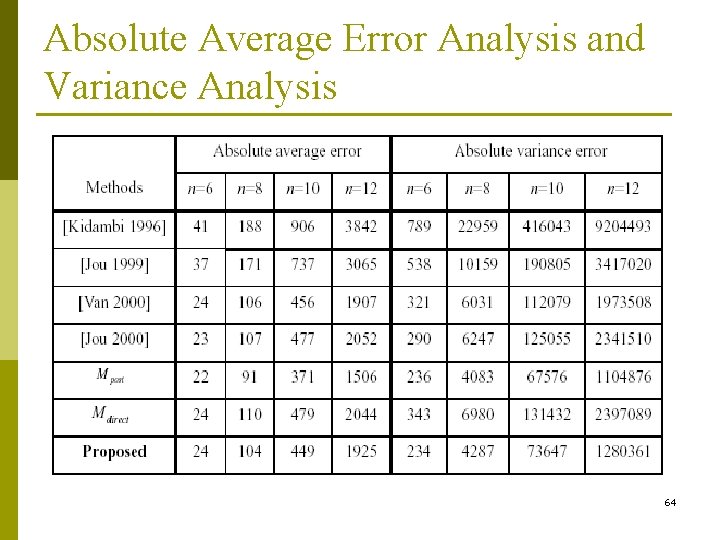
Absolute Average Error Analysis and Variance Analysis 64

Area ratios of three kinds of BSD fixed-width multipliers 65

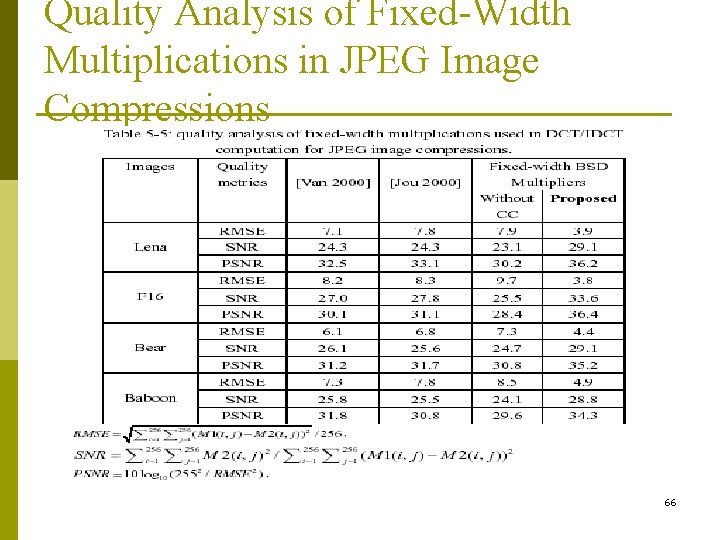
Quality Analysis of Fixed-Width Multiplications in JPEG Image Compressions 66

Summary p Our proposed fixed-width multipliers n Lower average errors and variances n Low-cost compensation circuits n Can be applied to high-speed DSP applications 67

Future Research Topics p p Chip Implementation of proposed CORDIC and fixed-width multipliers Low-power RNS multiplier design Automatic datapath synthesizer for embedded systems Design and analysis of high-speed dividers using proposed multipliers 68

Thank you very much, I love Dept. of IECS at Feng Chia! tsobing@cse. nsysu. edu. tw 0911878151 69