Parabola Conic section Warmup Graph the following parabola

Parabola Conic section

Warm-up Graph the following parabola using: I Finding the solution of the equations (Factoring) 1. y = 2 x - 6 x + 8 II Finding the VERTEX (Using formula) 2. y = 2 –x + 4 x – 4 III Graphing on y-axis (using vertex) 3. y = 2 x -5
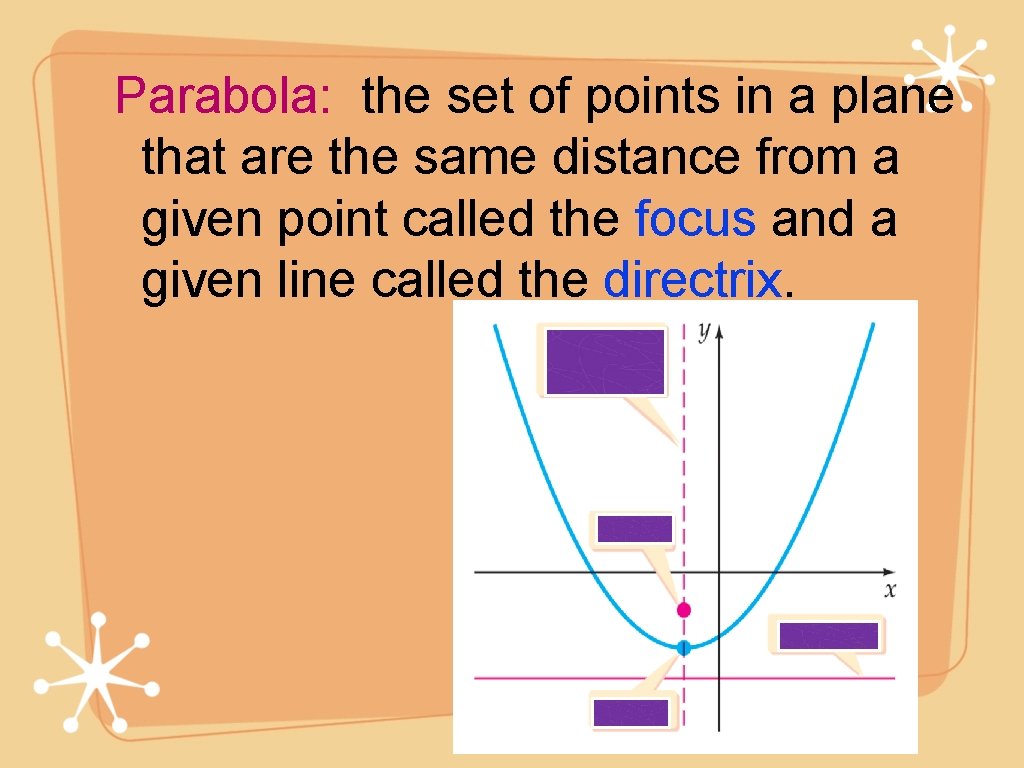
Parabola: the set of points in a plane that are the same distance from a given point called the focus and a given line called the directrix.
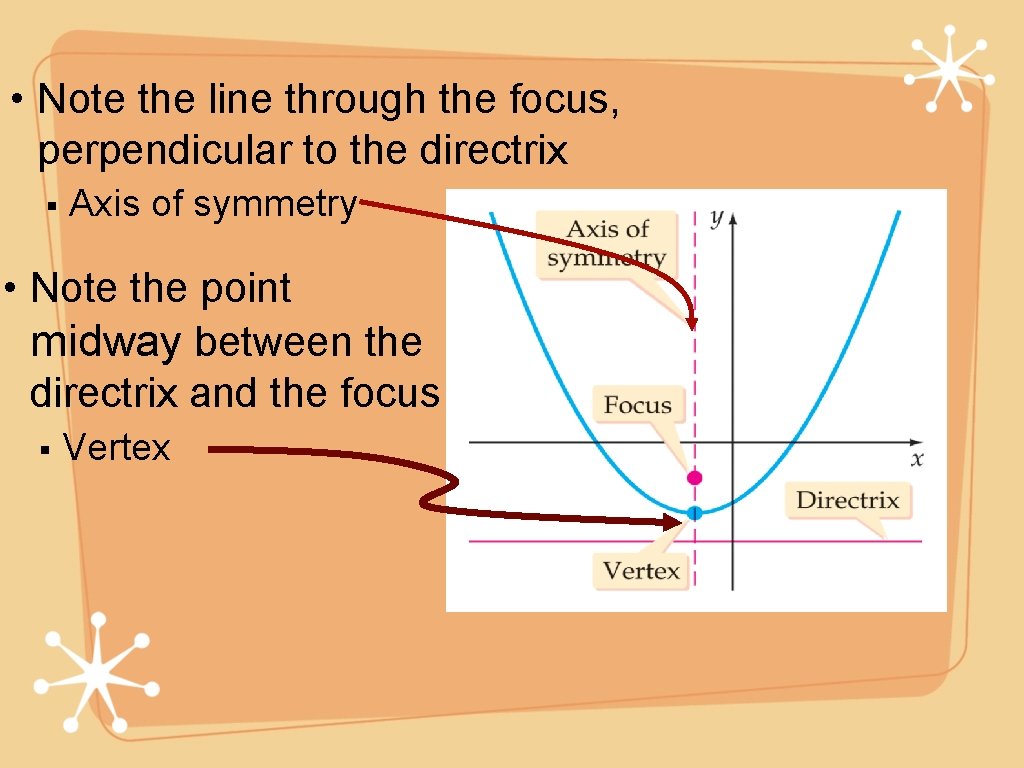
• Note the line through the focus, perpendicular to the directrix § Axis of symmetry • Note the point midway between the directrix and the focus § Vertex 4
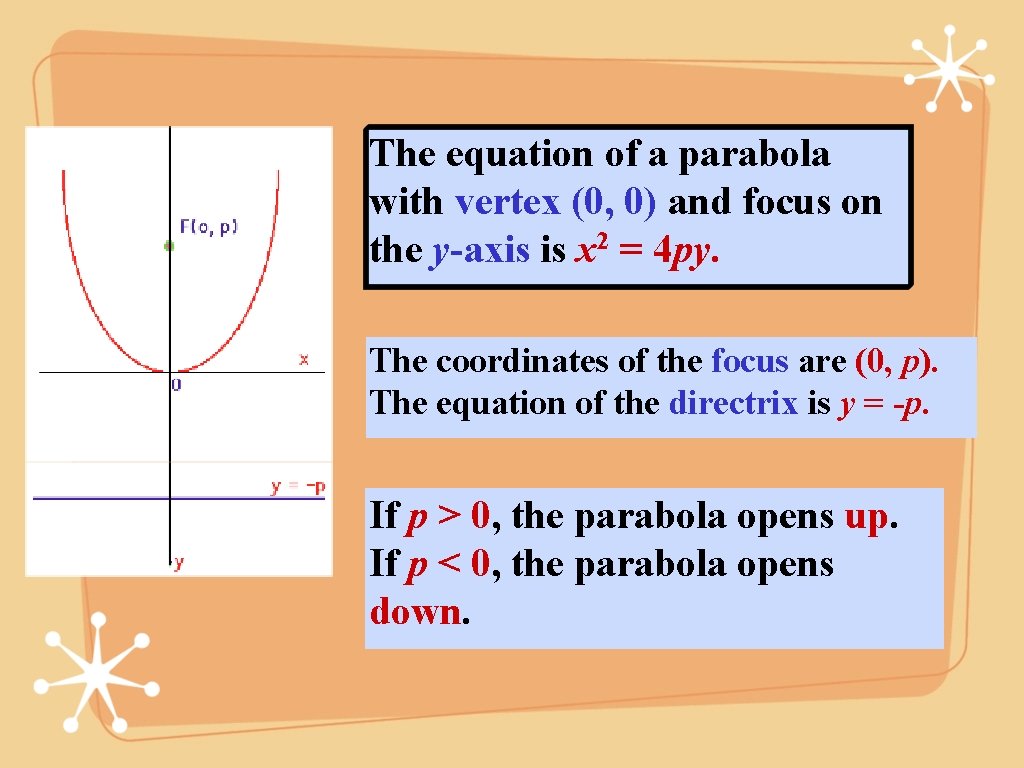
The equation of a parabola with vertex (0, 0) and focus on the y-axis is x 2 = 4 py. The coordinates of the focus are (0, p). The equation of the directrix is y = -p. If p > 0, the parabola opens up. If p < 0, the parabola opens down.
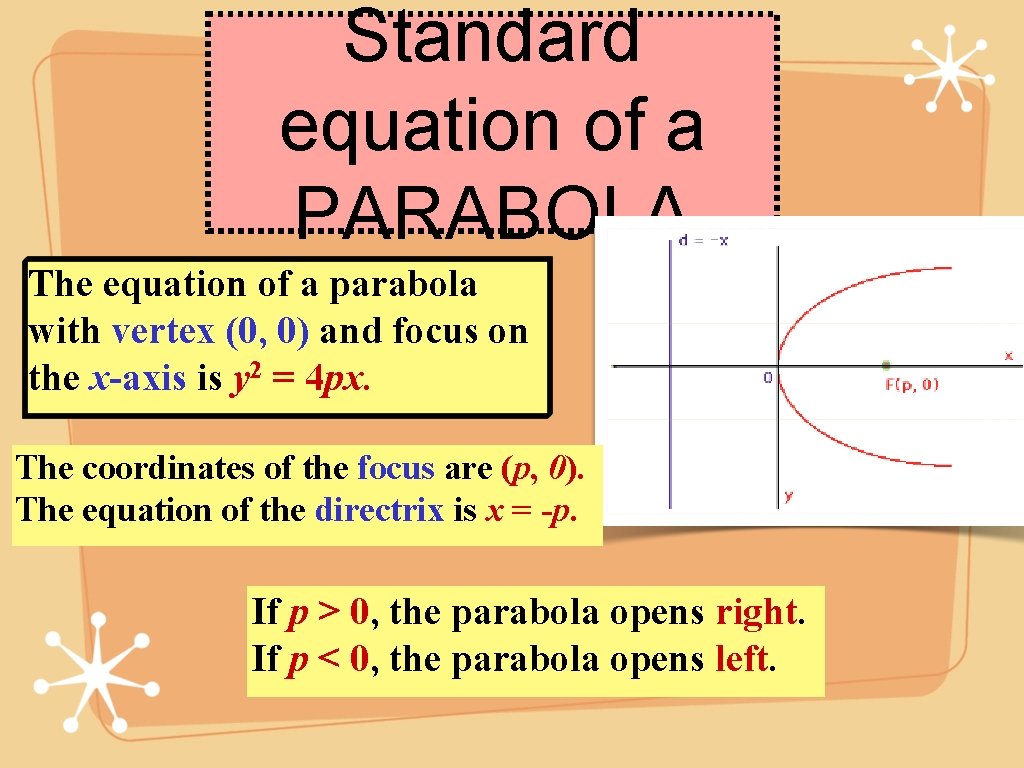
Standard equation of a PARABOLA The equation of a parabola with vertex (0, 0) and focus on the x-axis is y 2 = 4 px. The coordinates of the focus are (p, 0). The equation of the directrix is x = -p. If p > 0, the parabola opens right. If p < 0, the parabola opens left.

Finding the Equation of a A parabola has vertex. Vertex (0, 0) and the(0, focus 0) on an axis. Parabola with Write the equation of each parabola. a) The focus is (-6, 0). Since the focus is (-6, 0), the equation of the parabola is y 2 = 4 px. p is equal to the distance from the vertex to the focus, therefore p = -6. The equation of the parabola is y 2 = -24 x. b) The directrix is defined by x = 5. Since the focus is on the x-axis, the equation of the parabola is y 2 = 4 px. The equation of the directrix is x = -p, therefore -p = 5 or p = -5. The equation of the parabola is y 2 = -20 x. c) The focus is (0, 3). Since the focus is (0, 3), the equation of the parabola is x 2 = 4 py. p is equal to the distance from the vertex to the focus, therefore p = 3. The equation of the parabola is x 2 = 12 y.

Practice Finding the Equation of a A parabola has vertex. Vertex (0, 0) and the(0, focus 0) on an axis. Parabola with Write the equation of each parabola. a) The focus is (8, 0). The equation of the parabola is y 2 = 32 x. b) The directrix is defined by x = 3. The equation of the parabola is y 2 = -12 x. c) The focus is (0, -5). The equation of the parabola is x 2 = -20 y.

Finding the FOCUS y= DIRECTRIX 2 4 x x= 2 -3 y y = 4(4 py) x = -3(4 px) y = 16 py x = -12 px 1 = 16 p 1 = -12 p 1/16 = p -1/12 = p FOCUS: (0, 1/16) FOCUS: (-1/12, 0) Directrix Y = - 1/16 Directrix x = 1/12

Practice y= 2 8 x x= 2 -4 y FOCUS: (0, 1/32) FOCUS: (-1/16, 0) Directrix Y = - 1/32 Directrix x = 1/16

Parabola Conic section
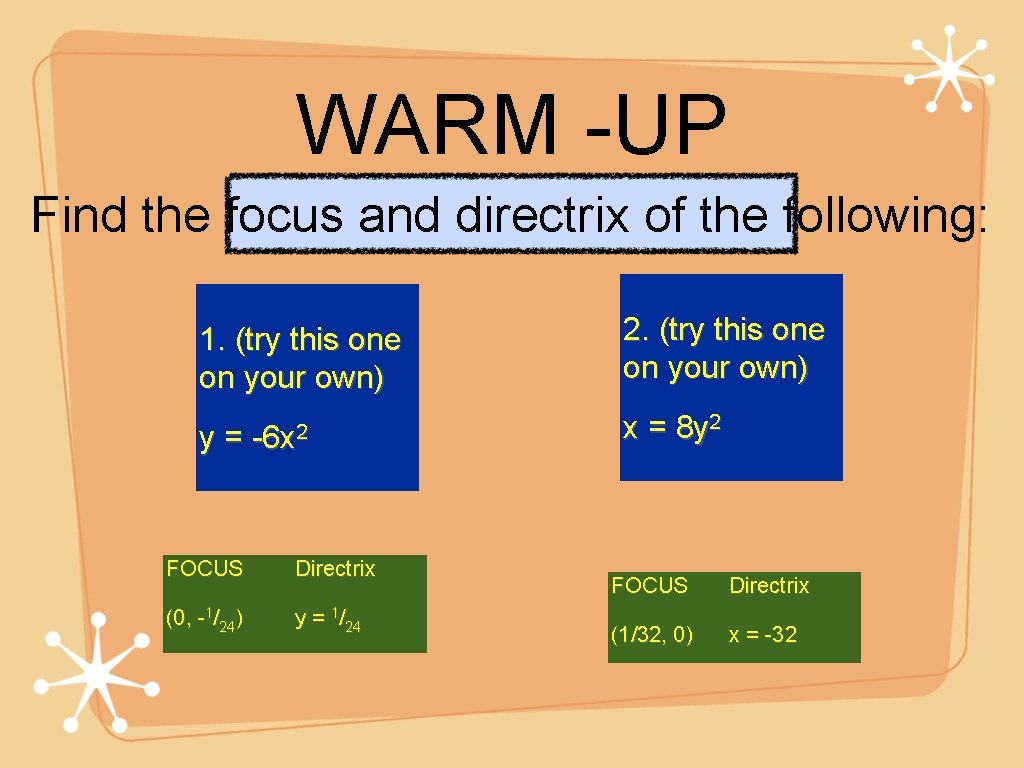
WARM -UP Find the focus and directrix of the following: 1. (try this one on your own) y= -6 x 2 FOCUS Directrix (0, -1/24) y = 1/24 2. (try this one on your own) x = 8 y 2 FOCUS Directrix (1/32, 0) x = -32
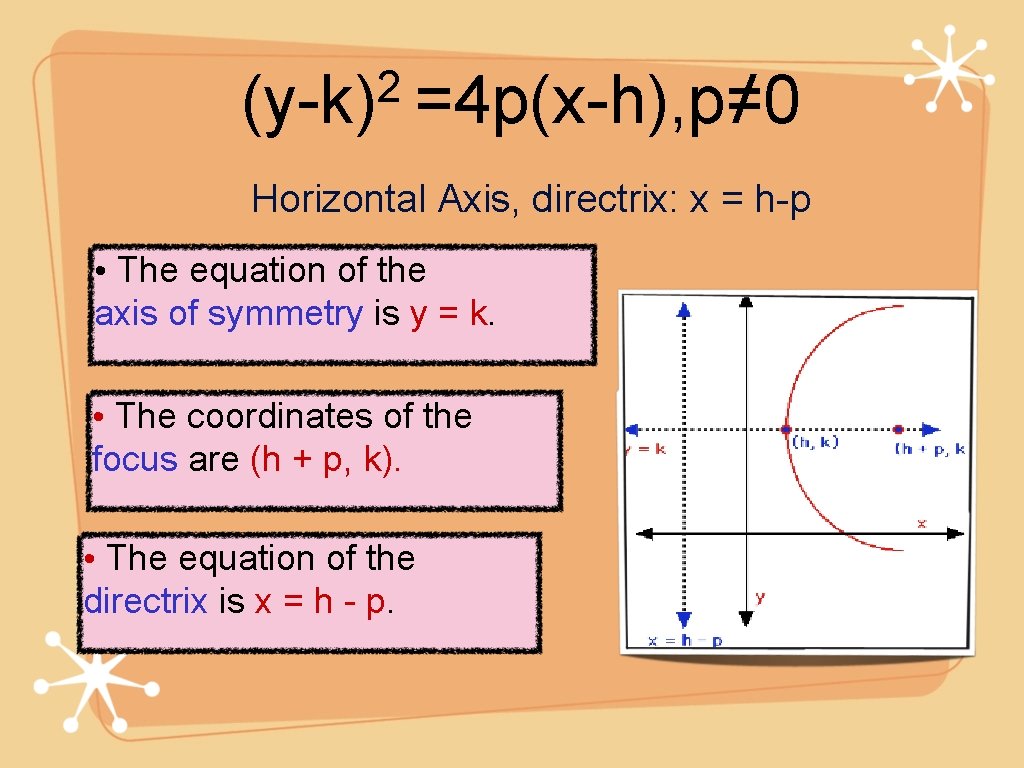
2 (y-k) =4 p(x-h), p≠ 0 Horizontal Axis, directrix: x = h-p • The equation of the axis of symmetry is y = k. • The coordinates of the focus are (h + p, k). • The equation of the directrix is x = h - p.

Ex: Write the equation of the parabola with a focus at (3, 5) and the directrix at x = 9, in standard form and general form. The distance from the focus to the directrix is 6 units, therefore, 2 p = -6, p = -3. Thus, the vertex is (6, 5). The axis of symmetry is parallel to the x-axis: (y - k)2 = 4 p(x - h) h = 6 and k = 5 (y - 5)2 = 4(-3)(x - 6) (y - 5)2 = -12(x - 6) Standard form y 2 - 10 y + 25 = -12 x + 72 y 2 + 12 x - 10 y - 47 = 0 General form

Practice Write the equation of the parabola with a focus at (4, 6) and the directrix at x = 8, in standard form and general form. Vertex: (6, 6) (y-6)2 = -8(x-6) Standard Form 2 y + 8 x -12 y -12 General Form
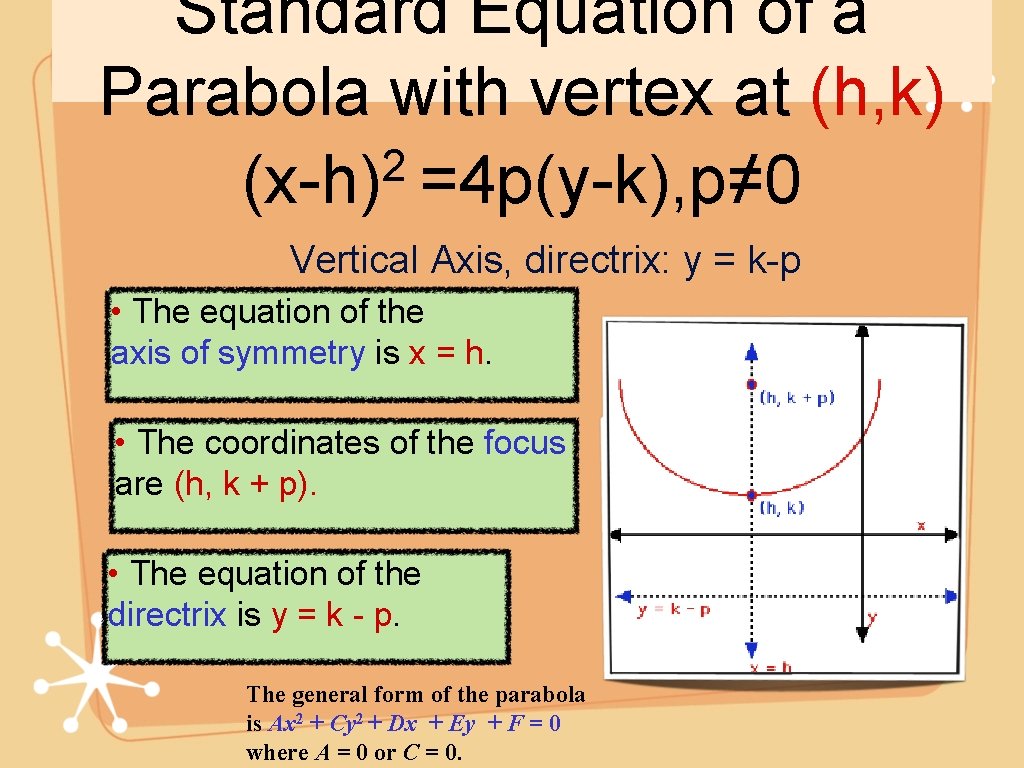
Standard Equation of a Parabola with vertex at (h, k) 2 (x-h) =4 p(y-k), p≠ 0 Vertical Axis, directrix: y = k-p • The equation of the axis of symmetry is x = h. • The coordinates of the focus are (h, k + p). • The equation of the directrix is y = k - p. The general form of the parabola is Ax 2 + Cy 2 + Dx + Ey + F = 0 where A = 0 or C = 0.

Find the equation of the parabola that has a min at (-2, 6) and passes through the point (2, 8). The axis of symmetry is parallel to the y-axis. The vertex is (-2, 6), therefore, h = -2 and k = 6. Substitute into the standard form of the equation and solve for p: (x - h)2 = 4 p(y - k) x = 2 and y = 8 (2 - (-2))2 = 4 p(8 - 6) 16 = 8 p 2=p (x - h)2 = 4 p(y - k) (x - (-2))2 = 4(2)(y - 6) (x + 2)2 = 8(y - 6) x 2 + 4 x + 4 = 8 y - 48 x 2 + 4 x - 8 y + 52 = 0 Standard form General form

homework Find the equation of the parabola that has a maximum at (3, 6) and passes through the point (9, 5). Vertex: (3, 6) (x-3)2 = -36(y-6) Standard Form 2 x - 6 x +36 y -207 General Form

Find the equation of the parabola that has a vertex at (2, 1) and focus (2, 4). 2 (x-h) h=2, = 4 p (y-k) k=1, p= 4 -1 = 3 (x-2)2 = 4(3) (y-1) 2 (x-2) 2 X = 12 (y-1) - 4 x -12 y + 16 = 0 Standard Form General Form

• The equation of the axis of symmetry is y = k. • The coordinates of the focus are (h + p, k). • The equation of the directrix is x = h - p. • The equation of the axis of symmetry is x = h. • The coordinates of the focus are (h, k + p). • The equation of the directrix is y = k - p.

Find the coordinates of the vertex and focus, Analyzing a Parabola the equation of the directrix, the axis of symmetry, and the direction of opening of y 2 - 8 x - 2 y - 15 = 0 y 2 - 2 y + _____ 1 = 8 x + 15 + _____ 1 (y - 1)2 = 8 x + 16 (y - 1)2 = 8(x + 2) Standard form 4 p = 8 p=2 The vertex is (-2, 1). The focus is (0, 1). The equation of the directrix is x + 4 = 0. The axis of symmetry is y - 1 = 0. The parabola opens to the right.

Finding the FOCUS y= DIRECTRIX 2 4 x x= 2 -3 y y = 4(4 py) x = -3(4 px) y = 16 py x = -12 px 1 = 16 p 1 = -12 p 1/16 = p -1/12 = p FOCUS: (0, 1/16) FOCUS: (-1/12, 0) Directrix Y = - 1/16 Directrix x = 1/12
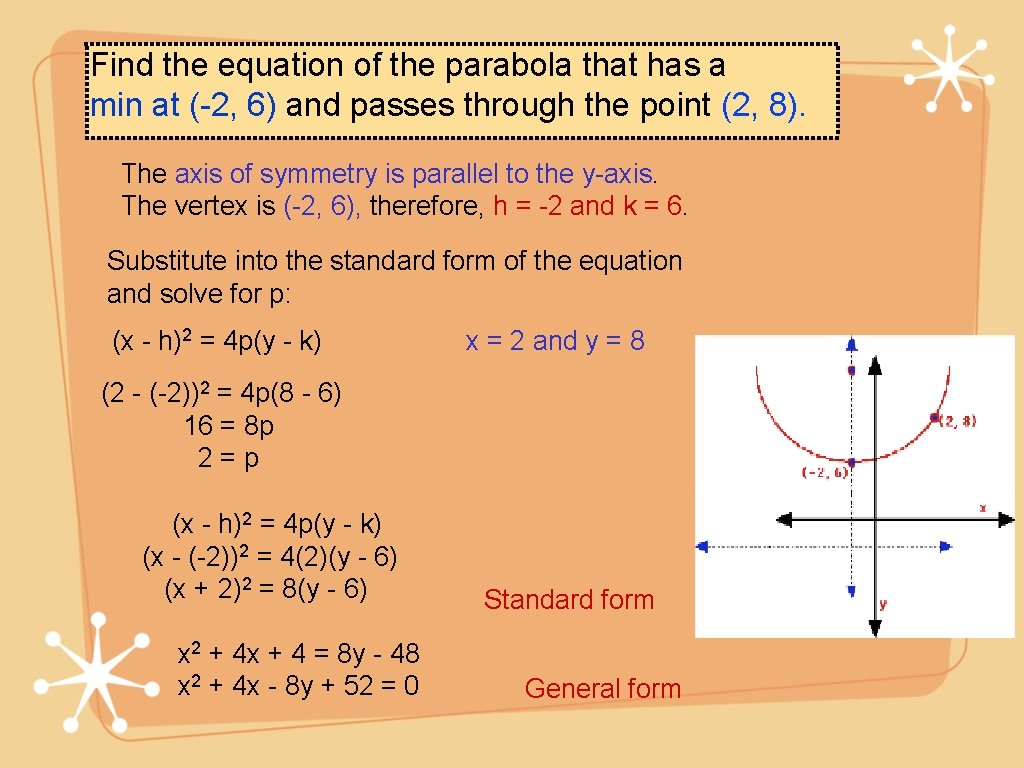
Find the equation of the parabola that has a min at (-2, 6) and passes through the point (2, 8). The axis of symmetry is parallel to the y-axis. The vertex is (-2, 6), therefore, h = -2 and k = 6. Substitute into the standard form of the equation and solve for p: (x - h)2 = 4 p(y - k) x = 2 and y = 8 (2 - (-2))2 = 4 p(8 - 6) 16 = 8 p 2=p (x - h)2 = 4 p(y - k) (x - (-2))2 = 4(2)(y - 6) (x + 2)2 = 8(y - 6) x 2 + 4 x + 4 = 8 y - 48 x 2 + 4 x - 8 y + 52 = 0 Standard form General form

Ex: Write the equation of the parabola with a focus at (3, 5) and the directrix at x = 9, in standard form and general form. The distance from the focus to the directrix is 6 units, therefore, 2 p = -6, p = -3. Thus, the vertex is (6, 5). The axis of symmetry is parallel to the x-axis: (y - k)2 = 4 p(x - h) h = 6 and k = 5 (y - 5)2 = 4(-3)(x - 6) (y - 5)2 = -12(x - 6) Standard form y 2 - 10 y + 25 = -12 x + 72 y 2 + 12 x - 10 y - 47 = 0 General form
- Slides: 24