Parabola Conic section Quadratic Functions The graph of

Parabola Conic section

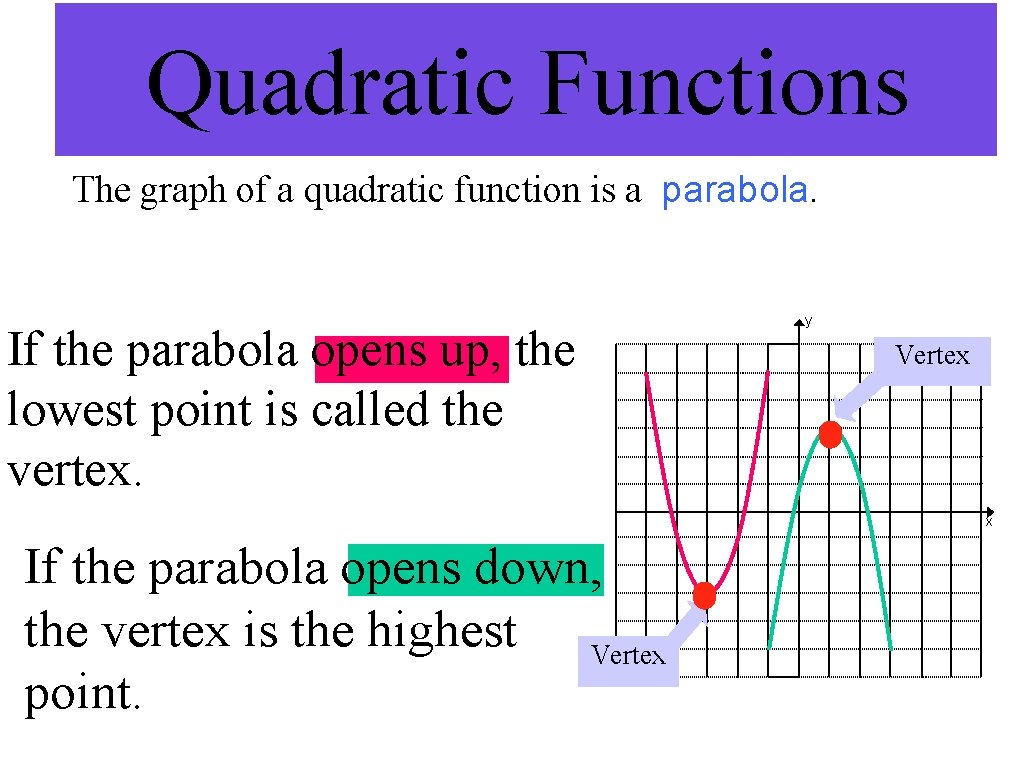
Quadratic Functions The graph of a quadratic function is a parabola. If the parabola opens up, the lowest point is called the vertex. y Vertex x If the parabola opens down, the vertex is the highest Vertex point.

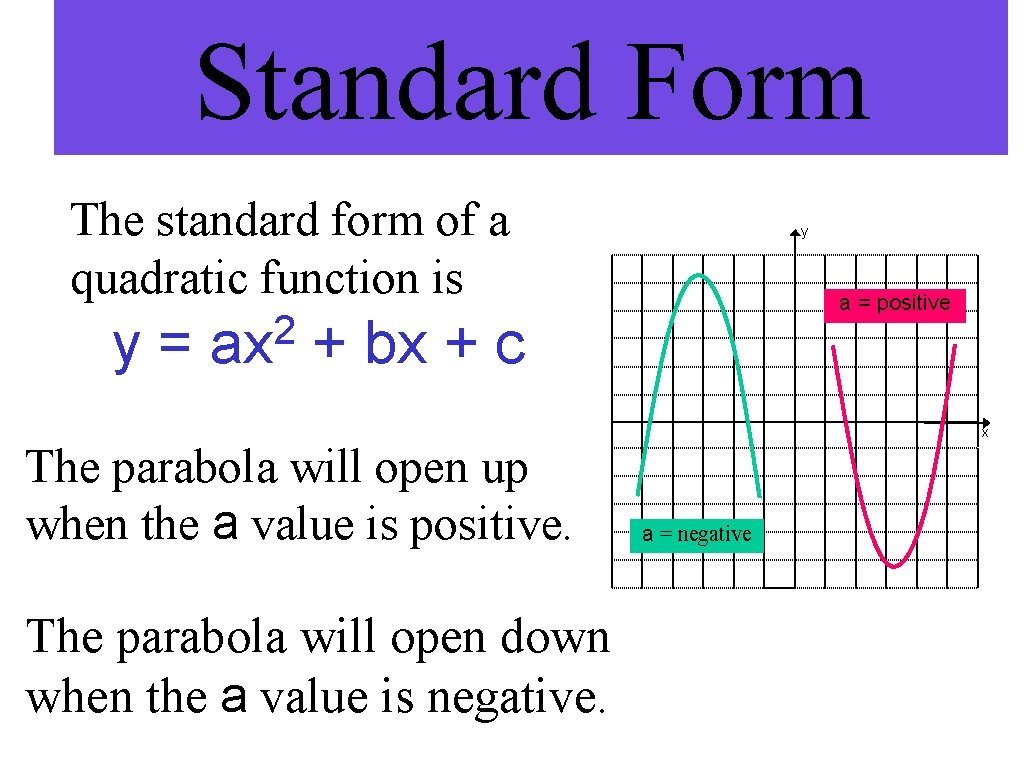
Standard Form The standard form of a quadratic function is y= 2 ax y a = positive + bx + c The parabola will open up when the a value is positive. The parabola will open down when the a value is negative. x a = negative

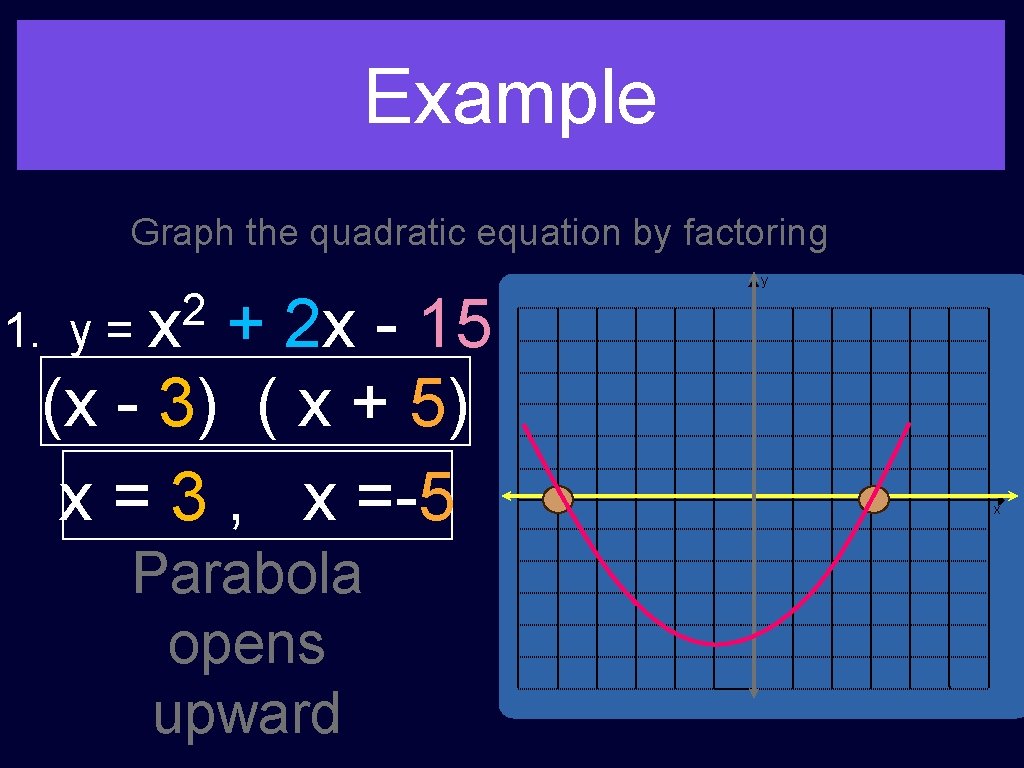
Example Graph the quadratic equation by factoring 2 1. y = x + 2 x - 15 (x - 3) ( x + 5) x = 3 , x =-5 Parabola opens upward y x

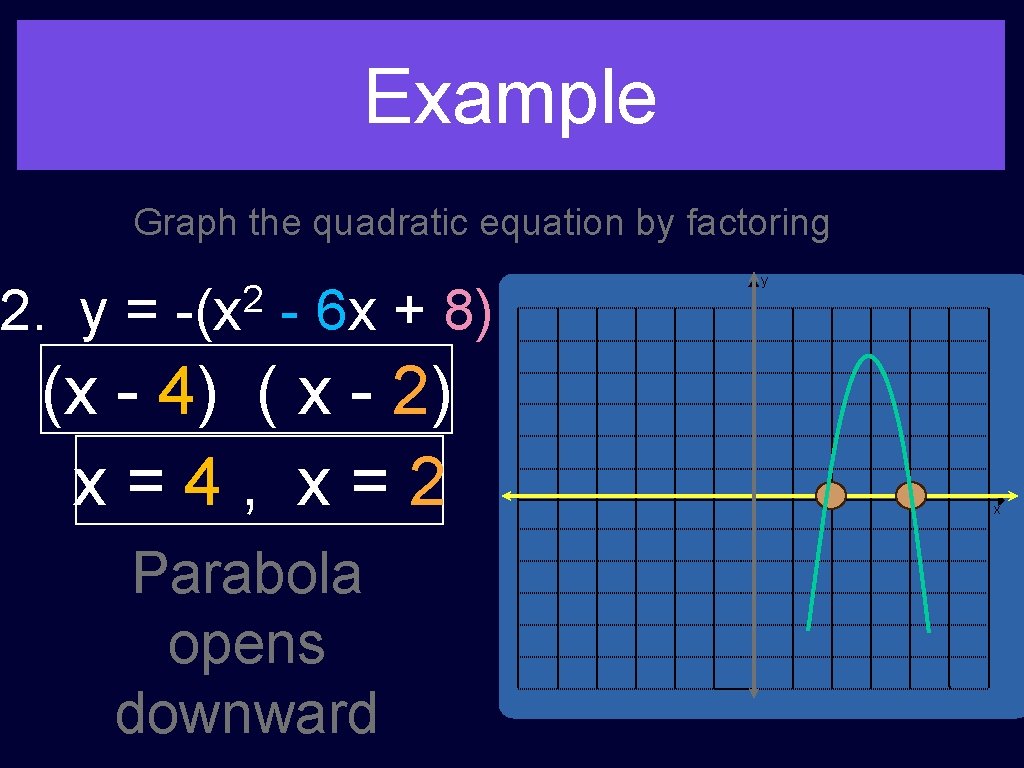
Example Graph the quadratic equation by factoring 2. y = 2 -(x - 6 x + 8) (x - 4) ( x - 2) x=4, x=2 Parabola opens downward y x

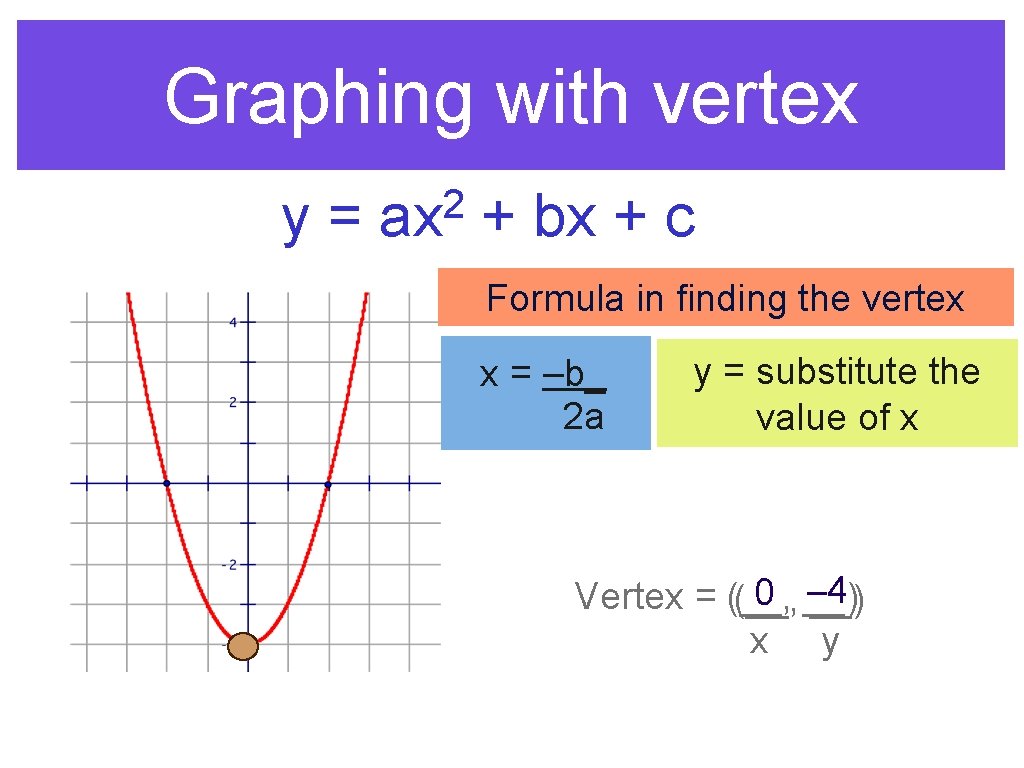
Graphing with vertex y= 2 ax + bx + c Formula in finding the vertex x = –b_ 2 a y = substitute the value of x –__) 4 0 __) Vertex = (__, x y

Example Find the vertex of y 2 = -3 x + 6 x + 5 x = –b_ 2 a x = – 6 2(-3) x = – 6 x=1 Formula in finding the vertex x = –b_ 2 a y = substitute the value of x y= 2 -3 x + 6 x + 5 y = -3(1)2 + 6(1) + 5 y = -3 + 6 + 5 y=8 Vertex = (1, 8)

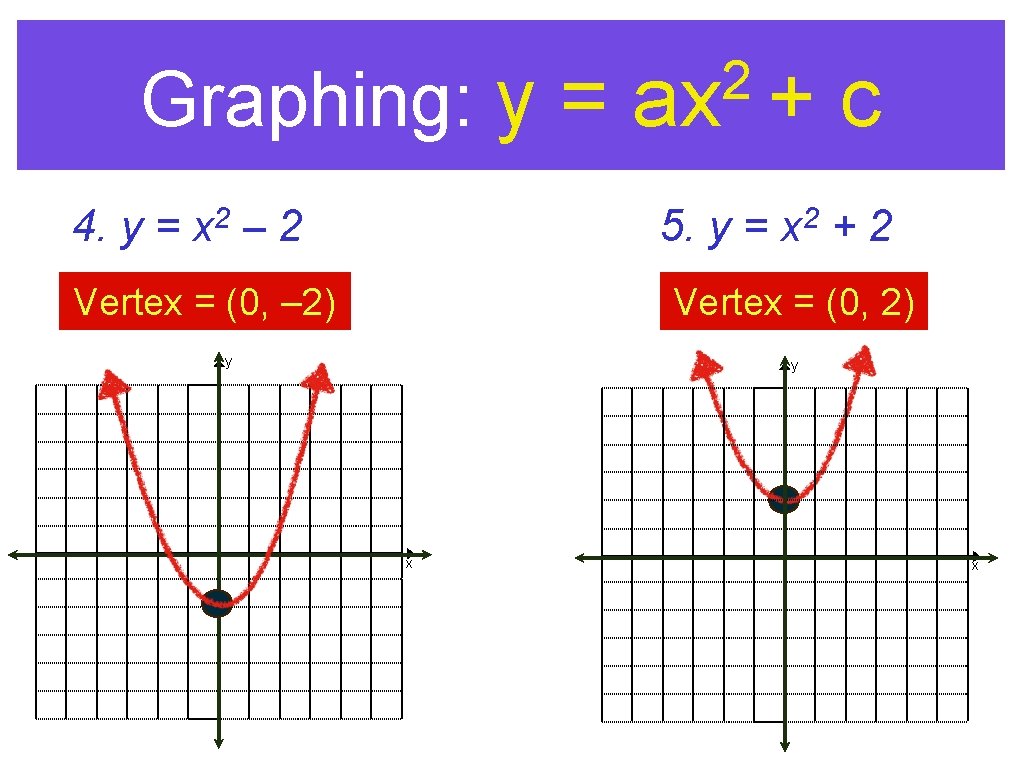
Graphing: y = 4. y = 2 x – 2 2 ax + 5. y = Vertex = (0, – 2) 2 x c +2 Vertex = (0, 2) y y x x

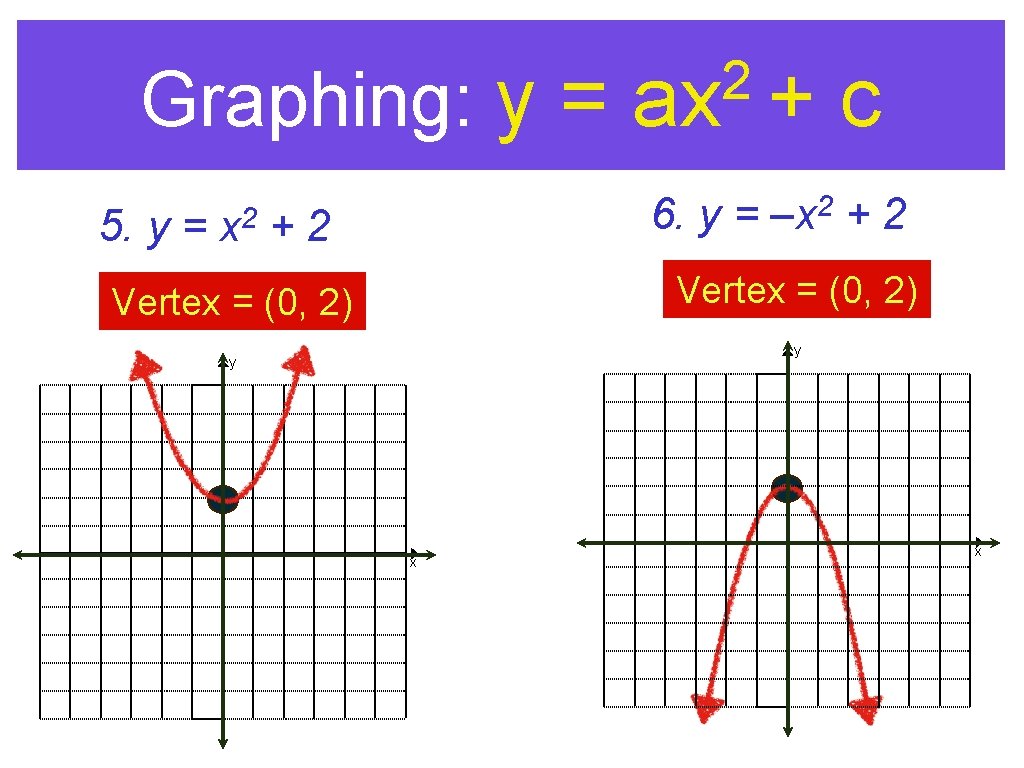
Graphing: y = 5. y = 2 x 2 ax + 6. y = +2 2 –x c +2 Vertex = (0, 2) y y x x

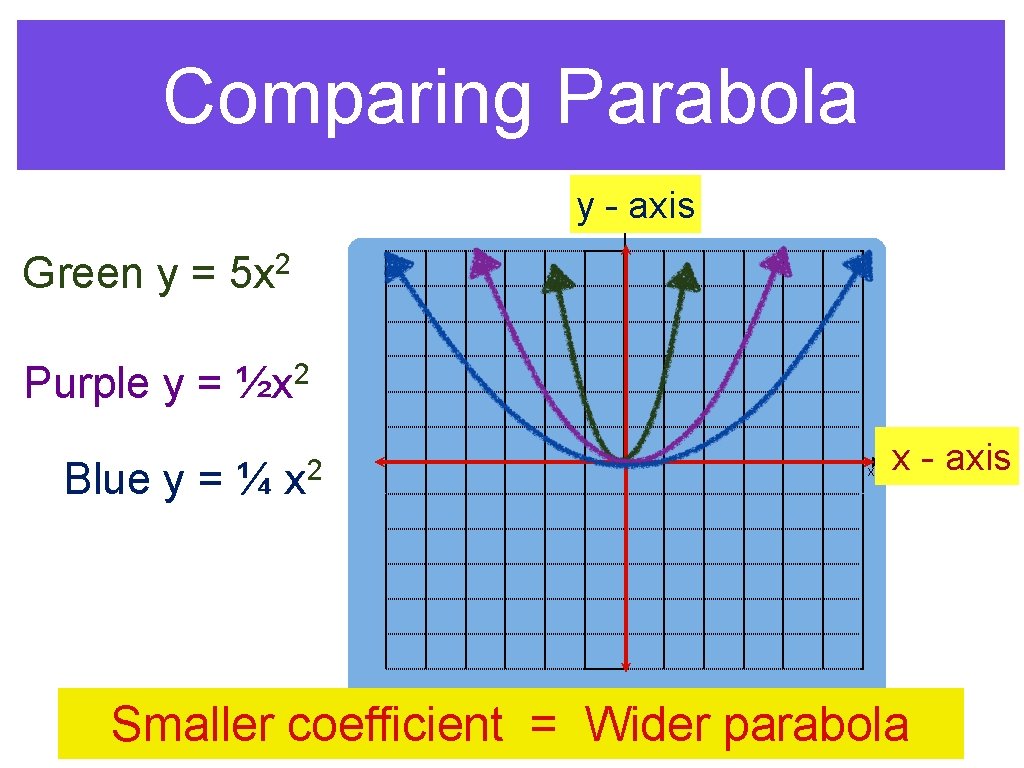
Comparing Parabola y - axis y Green y = 2 5 x Purple y = ½x 2 Blue y = ¼ x 2 x x - axis Smaller coefficient = Wider parabola