Paper review of ENGG6140 Optimization Techniques Paper Review

Paper review of ENGG*6140 Optimization Techniques Paper Review -- Interior-Point Methods for LP Yanrong Hu Ce Yu Mar. 11, 2003

Outline General introduction n The original algorithm description n A variant of Karmarkar’s algorithm - a detailed simple example n Another example n More issues n

General introduction Interior-point methods for linear programming: § The most dramatic new development in operations research (linear programming) during the 1980 s. § Opened in 1984 by a young mathematician at AT&T Bell Labs, N. Karmarkar. § Polynomial-time algorithm and has great potential for solving huge linear programming problems beyond the reach of the simplex method. § Karmarkar’s method stimulated development in both interior-point and simplex methods.

General introduction Difference between Interior point methods and the simplex method The big difference between Interior point methods and the simplex method lies in the nature of trial solutions. Trial solutions Simplex method Interior-point method CPF (Corner Point Feasible) solutions Interior points (points inside the boundary of the feasible region) worst case: # iterations can increase complexity exponentially in the number of variables n: Polynomial time

Karmarkar’s original Algorithm Karmarkar assumes that the LP is given in Canonical form of the problem: Assumptions: To apply the algorithm to LP problem in standard form, a transformation is needed. Min s. t. Z = CX AX b X 0

Karmarkar’s original Algorithm An example of transformation from standard form to canonical form Min z = y 1+y 2 (z=cy) Min z=5 x 1 + 5 x 2 s. t. y 1+2 y 2 2 (AY b) s. t. 3 x 1+8 x 2+3 x 3 -2 x 4=0 (AX=0) y 1, y 2 0 x 1+ x 2+ x 3+ x 4=1 (1 X =1) xj 0, j=1, 2, 3, 4

Karmarkar’s original Algorithm The principal idea: The algorithm creates a sequence of points having decreasing values of the objective function. In the step, the point is brought into the center of the simplex by a projective transformation.

Karmarkar’s original Algorithm The steps of Karmarkar’s algorithm are: Step 0. start with the solution point and compute the step length parameters Step k. Define: and compute: X is brought to the center by:

A Variant The Affine Variant of Karmarkar’s Algorithm: Concept 1: Shoot through the interior of the feasible region toward an interior optimal solution. Concept 2: Move in a direction that improves the objective function value at the fastest feasible rate. fastest Concept 3: Transform the feasible region to place the current trail solution Transform near its center, thereby enabling a large improvement when center concept 2 is implemented.

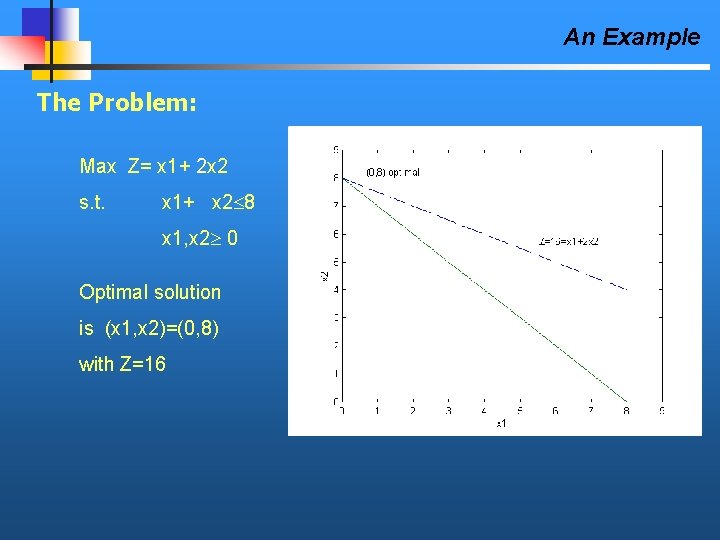
An Example The Problem: Max Z= x 1+ 2 x 2 s. t. x 1+ x 2 8 x 1, x 2 0 Optimal solution is (x 1, x 2)=(0, 8) with Z=16

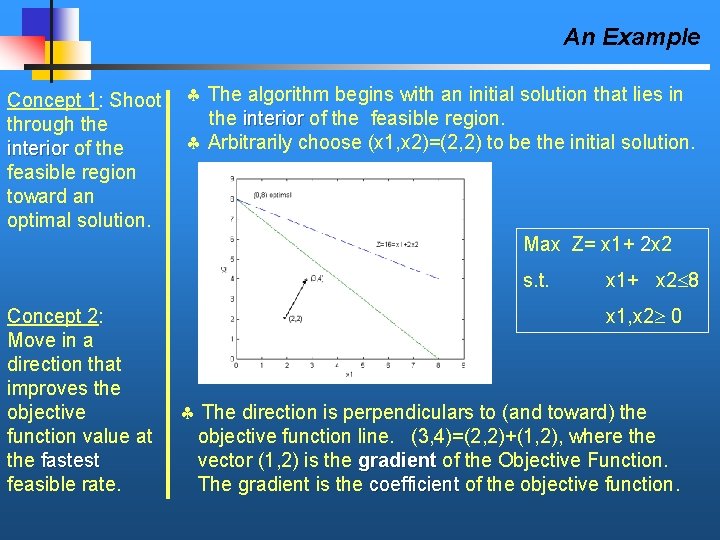
An Example Concept 1: Shoot The algorithm begins with an initial solution that lies in the interior of the feasible region. interior through the Arbitrarily choose (x 1, x 2)=(2, 2) to be the initial solution. interior of the interior feasible region toward an optimal solution. Max Z= x 1+ 2 x 2 s. t. Concept 2: Move in a direction that improves the objective function value at the fastest feasible rate. x 1+ x 2 8 x 1, x 2 0 The direction is perpendiculars to (and toward) the objective function line. (3, 4)=(2, 2)+(1, 2), where the vector (1, 2) is the gradient of the Objective Function. gradient The gradient is the coefficient of the objective function. coefficient

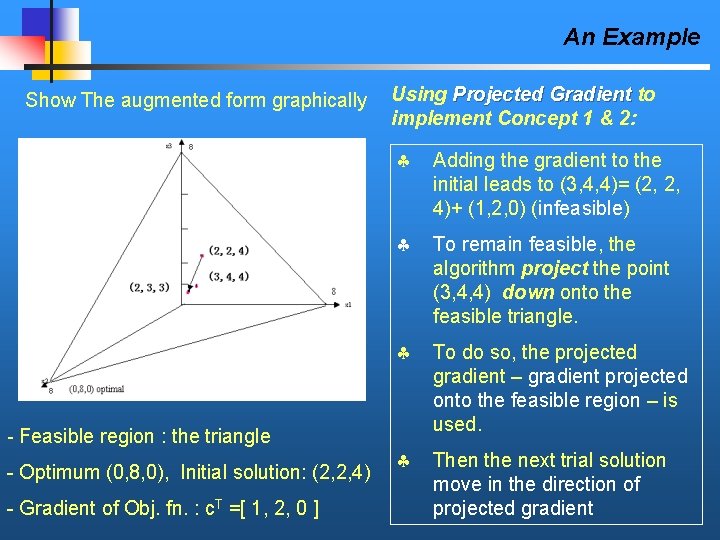
An Example The algorithm actually operates on the augmented form. The augmented form can be Max Z = c. T X written in general as: s. t. AX = b X 0 Max Z = x 1+ 2 x 2 s. t. letting x 3 be the slack x 1+ x 2 8 s. t. x 1+ x 2+ x 3 = 8 x 1, x 2 0 Initial solution: Max Z = x 1+ 2 x 2 x 1, x 2, x 3 0 (2, 2) (2, 2, 4) Gradient of obj. fn. : (1, 2) (1, 2, 0)

An Example Show The augmented form graphically - Feasible region : the triangle - Optimum (0, 8, 0), Initial solution: (2, 2, 4) - Gradient of Obj. fn. : c. T =[ 1, 2, 0 ] Using Projected Gradient to implement Concept 1 & 2: Adding the gradient to the initial leads to (3, 4, 4)= (2, 2, 4)+ (1, 2, 0) (infeasible) To remain feasible, the algorithm project the point (3, 4, 4) down onto the feasible triangle. To do so, the projected gradient – gradient projected onto the feasible region – is used. Then the next trial solution move in the direction of projected gradient

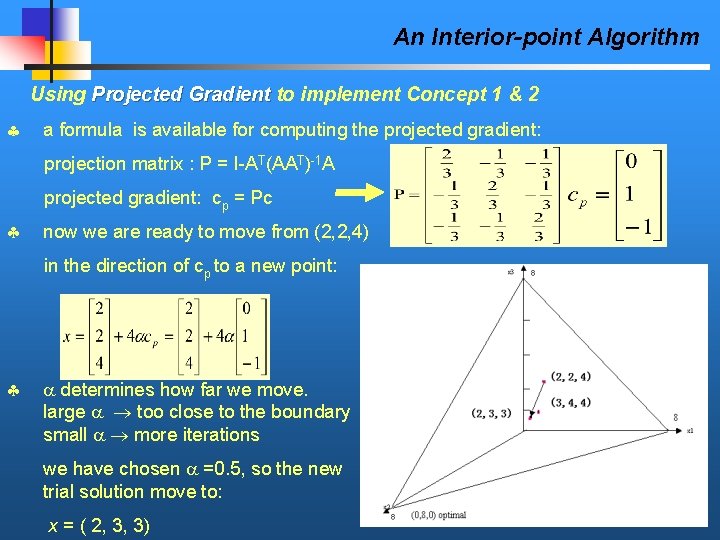
An Interior-point Algorithm Using Projected Gradient to implement Concept 1 & 2 a formula is available for computing the projected gradient: projection matrix : P = I-AT(AAT)-1 A projected gradient: cp = Pc now we are ready to move from (2, 2, 4) in the direction of cp to a new point: determines how far we move. large too close to the boundary small more iterations we have chosen =0. 5, so the new trial solution move to: x = ( 2, 3, 3)

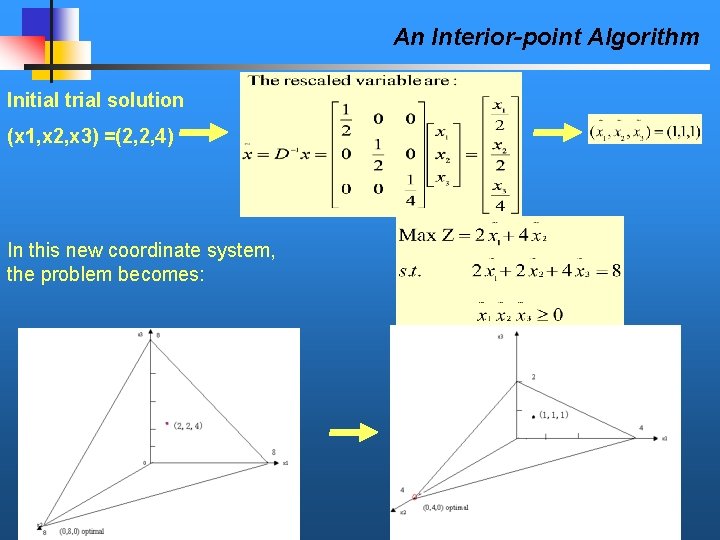
An Interior-point Algorithm Concept 3: Centering scheme for implementing Concept 3 Why -- The centering scheme keeps turning the direction of Transform the projected gradient to point more nearly toward an feasible region optimal solution as the algorithm converges toward this to place the solution. current trail solution How -- Simply changing the scale (units) for each of the changing the scale near its center, center variable so that the trail solution becomes equidistant from thereby enabling the constraint boundaries in the new coordinate system. a large Define D=diag{x}, improvement when concept 2 is implemented. bring x to the center coordinate in the new

An Interior-point Algorithm Initial trial solution (x 1, x 2, x 3) =(2, 2, 4) In this new coordinate system, the problem becomes:

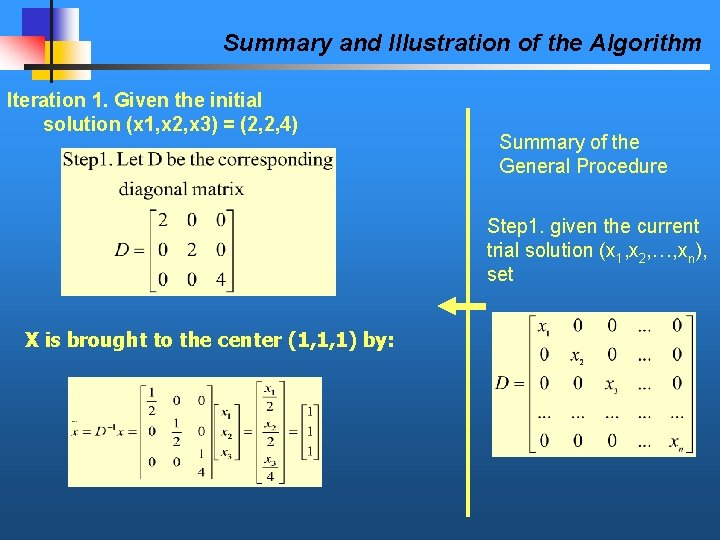
Summary and Illustration of the Algorithm Iteration 1. Given the initial solution (x 1, x 2, x 3) = (2, 2, 4) Summary of the General Procedure Step 1. given the current trial solution (x 1, x 2, …, xn), set X is brought to the center (1, 1, 1) by:

Summary and Illustration of the Algorithm Iteration 1. (cont. ) Summary of the General Procedure (cont. ) To compute projected gradient:

Summary and Illustration of the Algorithm Iteration 1. (cont. ) Summary of the General Procedure (cont. ) Compute projected gradient:

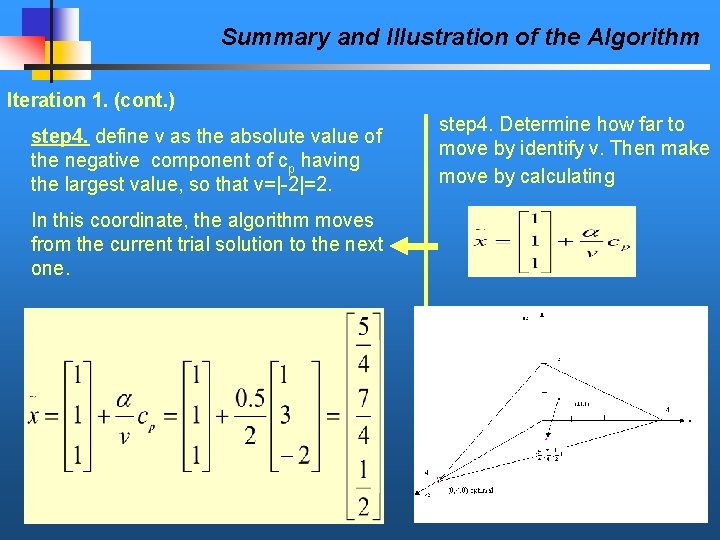
Summary and Illustration of the Algorithm Iteration 1. (cont. ) step 4. define v as the absolute value of the negative component of cp having the largest value, so that v=|-2|=2. In this coordinate, the algorithm moves from the current trial solution to the next one. step 4. Determine how far to move by identify v. Then make move by calculating

Summary and Illustration of the Algorithm Iteration 1. (cont. ) Step 5. In the original coordinate, the solution is Summary of the General Procedure (cont. ) Step 5. Back to the original coordinate by calculating this completes the iteration 1. The new solution will be used to start the next iteration.

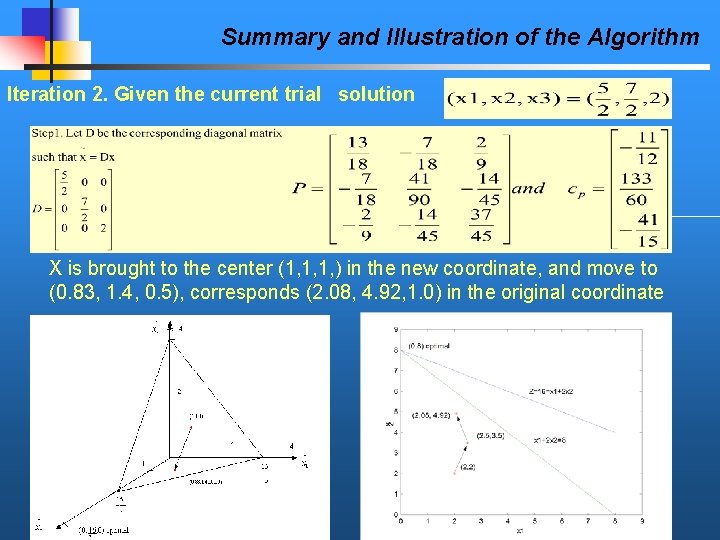
Summary and Illustration of the Algorithm Iteration 2. Given the current trial solution X is brought to the center (1, 1, 1, ) in the new coordinate, and move to (0. 83, 1. 4, 0. 5), corresponds (2. 08, 4. 92, 1. 0) in the original coordinate

Summary and Illustration of the Algorithm Iteration 3. Given the current trial solution x=(2. 08, 4. 92, 1. 0) X is brought to the center (1, 1, 1, ) in the new coordinate, and move to ( 0. 54, 1. 30, 0. 50), corresponds (1. 13, 6. 37, 0. 5) in the original coordinate

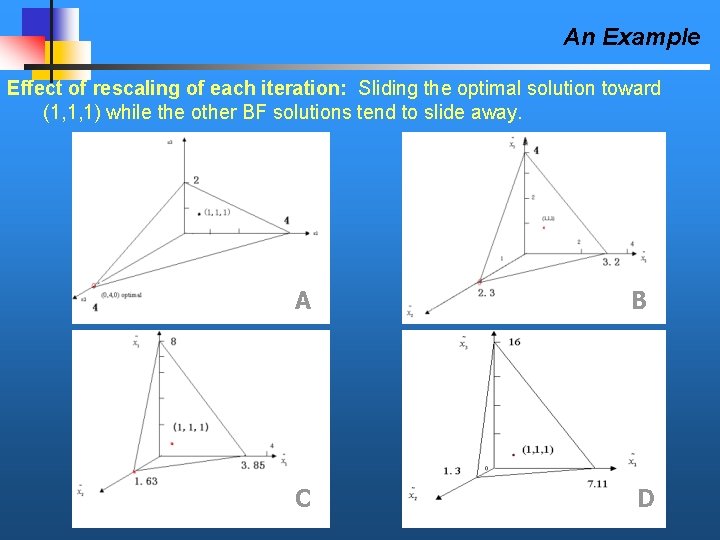
An Example Effect of rescaling of each iteration: Sliding the optimal solution toward (1, 1, 1) while the other BF solutions tend to slide away. A B C D

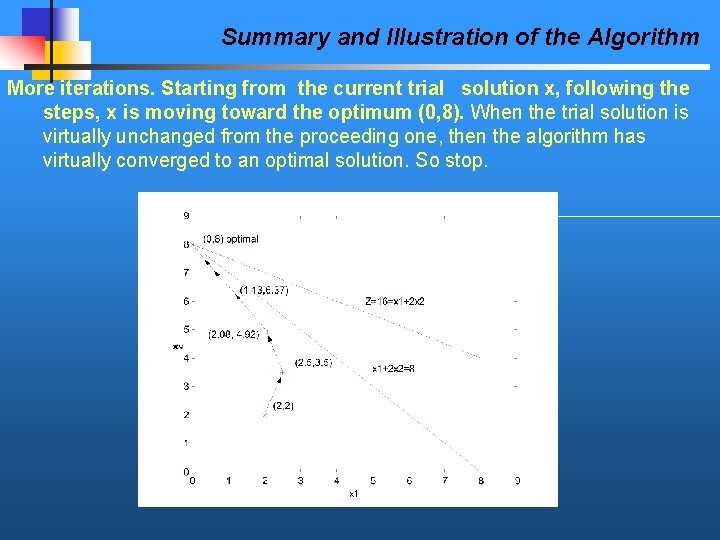
Summary and Illustration of the Algorithm More iterations. Starting from the current trial solution x, following the steps, x is moving toward the optimum (0, 8). When the trial solution is virtually unchanged from the proceeding one, then the algorithm has virtually converged to an optimal solution. So stop.

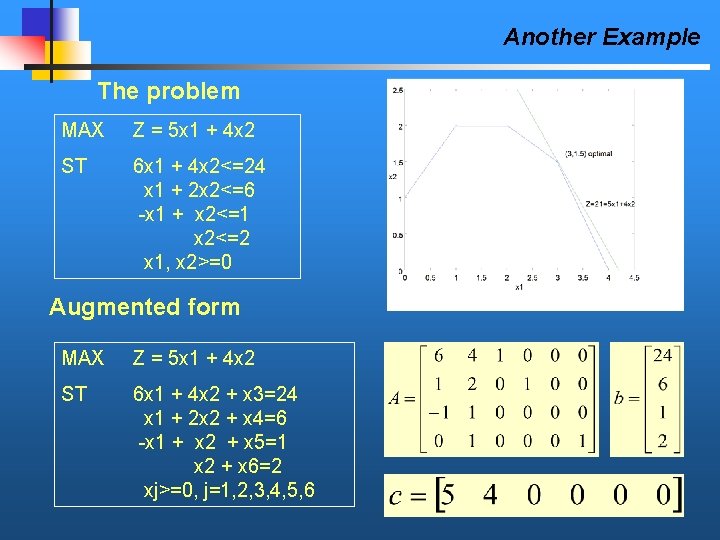
Another Example The problem MAX Z = 5 x 1 + 4 x 2 ST 6 x 1 + 4 x 2<=24 x 1 + 2 x 2<=6 -x 1 + x 2<=1 x 2<=2 x 1, x 2>=0 Augmented form MAX Z = 5 x 1 + 4 x 2 ST 6 x 1 + 4 x 2 + x 3=24 x 1 + 2 x 2 + x 4=6 -x 1 + x 2 + x 5=1 x 2 + x 6=2 xj>=0, j=1, 2, 3, 4, 5, 6

Another Example Starting from an initial solution x=(1, 1, 14, 3, 1, 1) The trial solution at each iteration

More issues v Interior-point methods is designed for dealing with big problems. Although the claim that it’s much faster than the simplex method is controversy, many tests on huge LP problems show its outperformance. v After Karmarkar’s paper, many related methods have been developed to extend the applicability of Karmarkar’s algorithm, e. g. • Infeasible interior points method -- remove the assumption that there always exits a nonempty interior. • Methods applying to LP problems in standard form.

More issues • Methods dealing with finding initial solution, and estimating the optimal solution. • Methods working with primal-dual problems. • Studies about moving step-long/short steps. • Studies about efficient implementation and complexity of various methods. v Karmarkar’s paper not only started the development of interior point methods, but also encouraged rapid improvement of simplex methods.

Reference [1] N. Karmarkar, 1984, A New Polynomial - Time Algorithm for Linear Programming, Combinatorica 4 (4), 1984, p. 373 -395. [2] M. J. Todd, (1994), Theory and Practice for Interior-point method, ORSA Jounal on Computing 6 (1), 1994, p. 28 -31. [3] I. Lustig, R. Marsten, D. Shanno, (1993), Interior-point Methods for Linear Programming: Computational State of the Art, ORSA Journal on Computing, 6 (1), 1994, p. 1 -14. [4] Hillier, Lieberman, Introduction to Operations Research (7 th edition) 320 -334 [5] Taha, Operations Research: An Introduction (6 th edition) 336 -345 [6] E. R. Barnes, 1986, A Variation on Karmarkar’s Algorithm for Sloving Linear Programming problems, Mathematical Programming 36, 1986, p. 174 -182. [7] R. J. Vanderbei, M. S. Meketon and B. A. Freeman, A Modification of karmarkar’s Linear Programming Algorithm, Algorithmica: An International Journal in Computer Science 1 (4), 1986 p. 395 – 407. [8] D. Gay (1985) A Variant of Karmarkar’s Linear Programming Algorithm for Problems in Standard form, Mathematical Programming 37 (1987) 81 -90 more…

Paper Review of ENGG*6140 Optimization Techniques Yanrong Hu Ce Yu Mar. 11 2003