PAM and QAM Data Communication Lecture 9 1












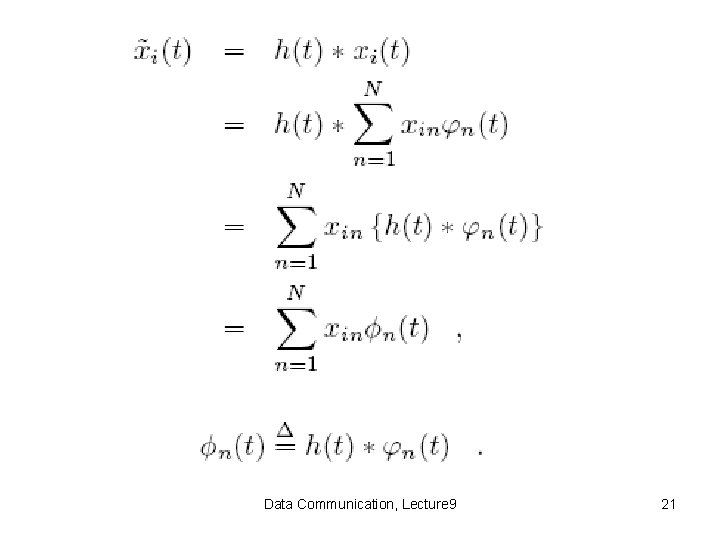








- Slides: 32

PAM and QAM Data Communication, Lecture 9 1

• Homework 1: exercises 1, 2, 3, 4, 9 from chapter 1 deadline: 85/2/19 Data Communication, Lecture 9 2

Data Communication, Lecture 9 3

Data Communication, Lecture 9 4

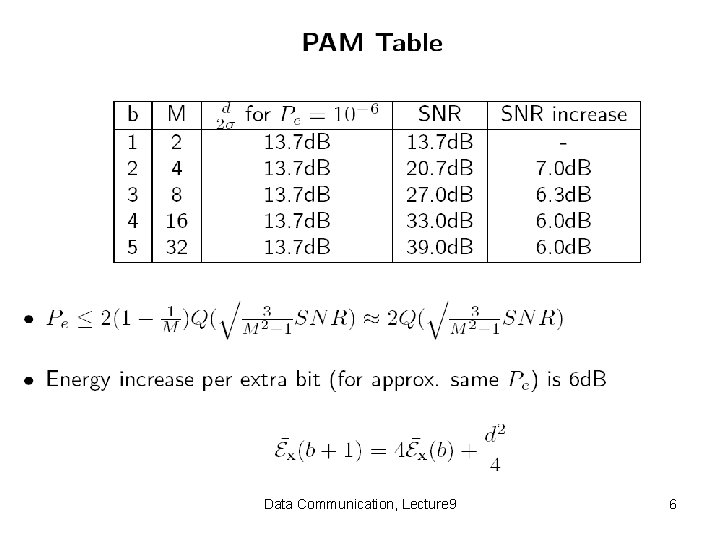
Data Communication, Lecture 9 5

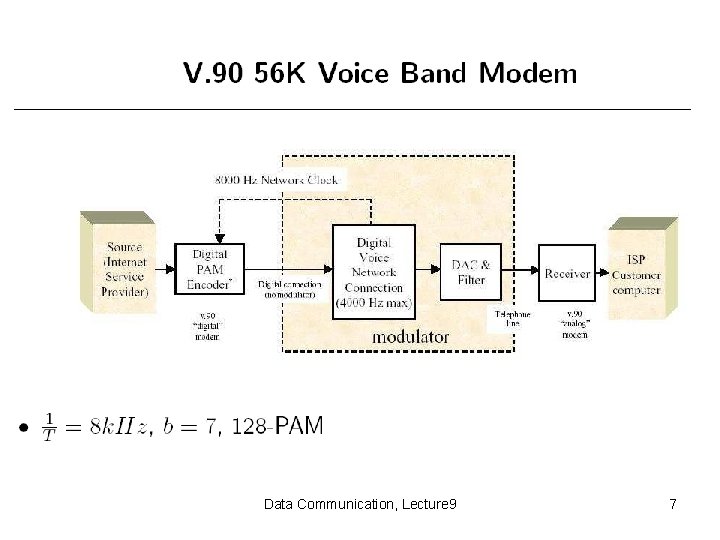
Data Communication, Lecture 9 6

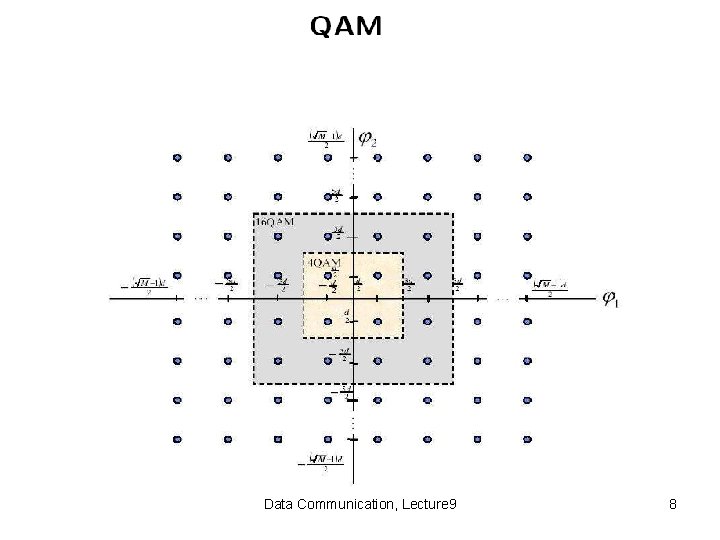
Data Communication, Lecture 9 7

Data Communication, Lecture 9 8

Data Communication, Lecture 9 9

Data Communication, Lecture 9 10

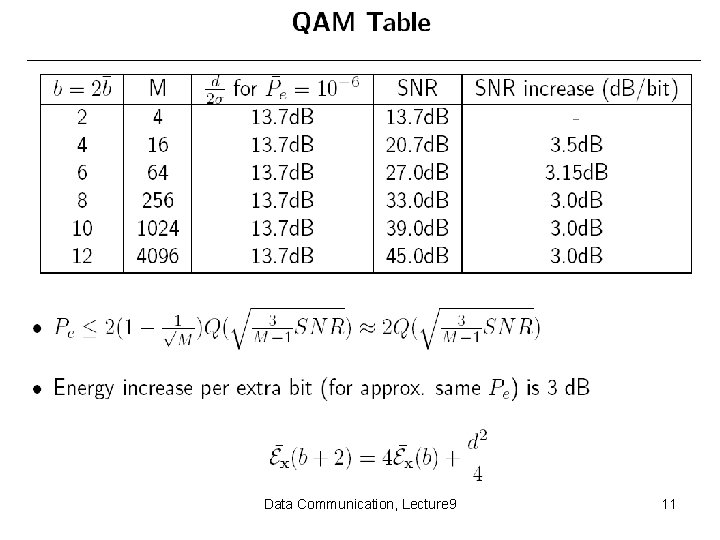
Data Communication, Lecture 9 11

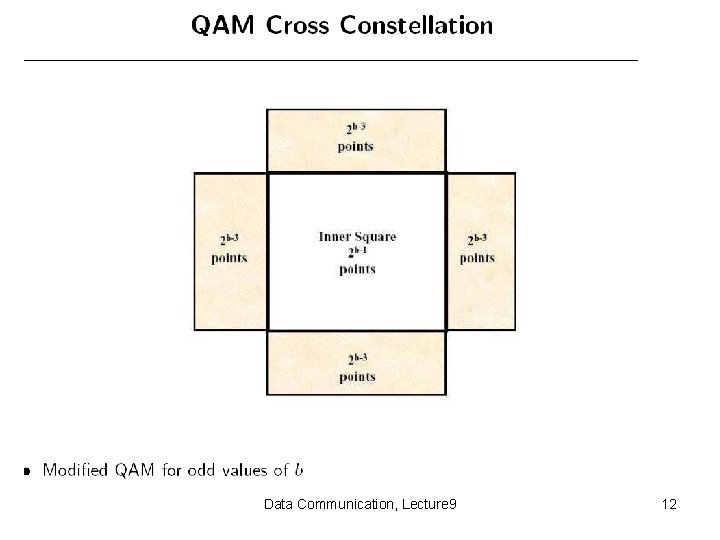
Data Communication, Lecture 9 12

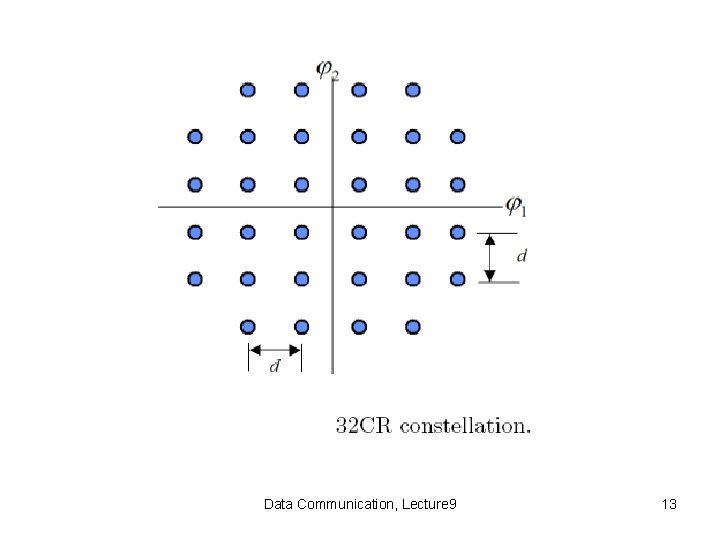
Data Communication, Lecture 9 13

Data Communication, Lecture 9 14

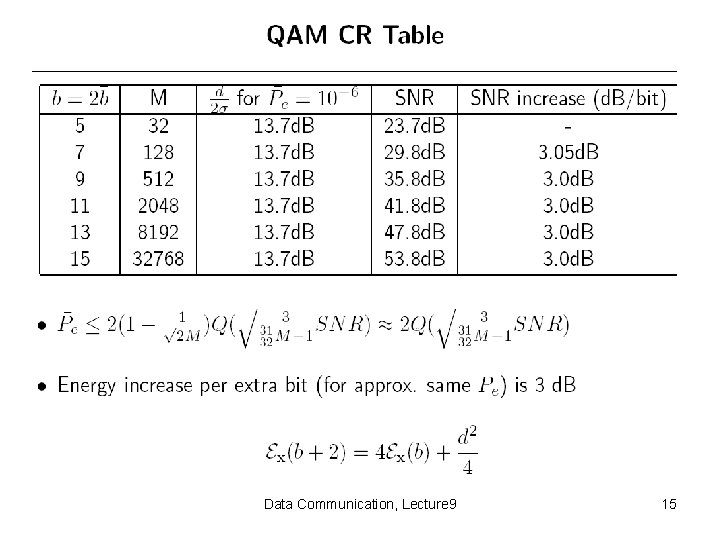
Data Communication, Lecture 9 15

Constellation Performance Measures Data Communication, Lecture 9 16

Data Communication, Lecture 9 17

• coding gain (or loss), of a particular constellation with data symbols {xi}, i=0, . . . , M− 1 with respect to another constellation with data symbols {~xi} is defined as where both constellations are used to transmit ¯b bits of information per dimension. Data Communication, Lecture 9 18

Data Communication, Lecture 9 19

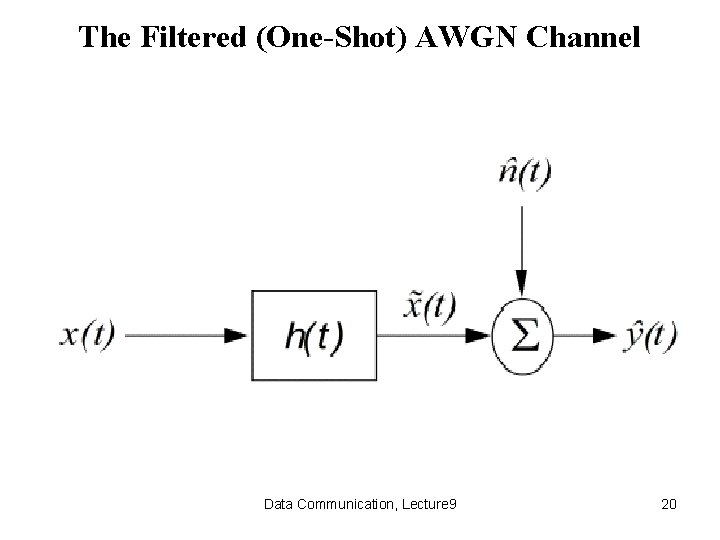
The Filtered (One-Shot) AWGN Channel Data Communication, Lecture 9 20
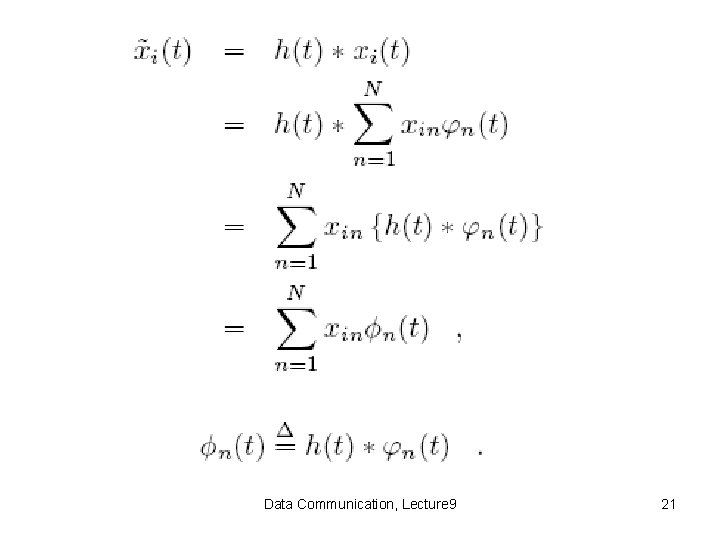
Data Communication, Lecture 9 21

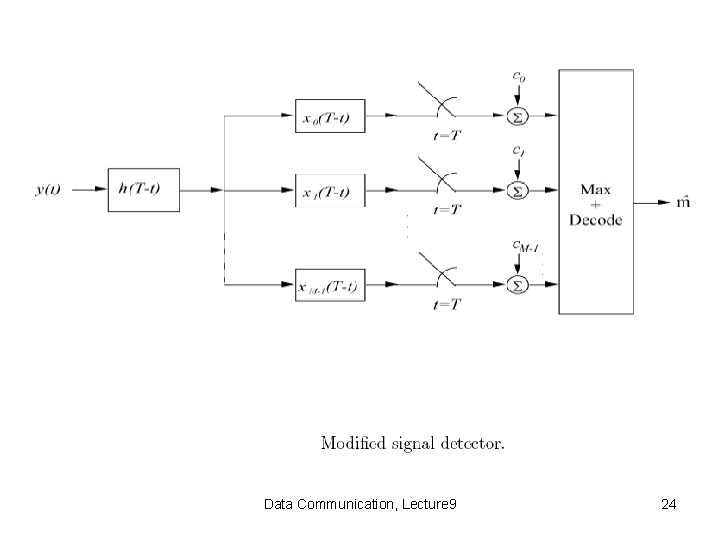
Note that: • The set of N functions {Φn(t)}n=1, . . . , N is not necessarily orthonormal. • For the channel to convey and all constellations of M messages for the signal set {xi(t)}, the basis set {Φn(t)} must be linearly independent. Data Communication, Lecture 9 22

Data Communication, Lecture 9 23

Data Communication, Lecture 9 24

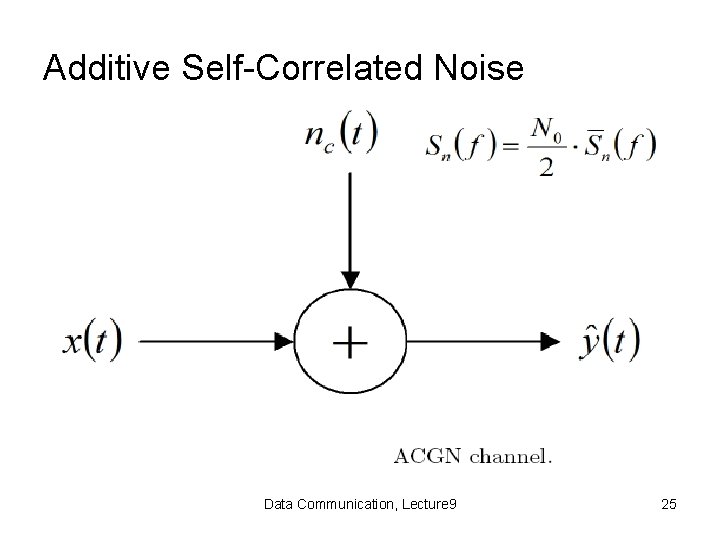
Additive Self-Correlated Noise Data Communication, Lecture 9 25

• In practice, additive noise is often Gaussian, but its power spectral density is not flat. • Engineers often call this type of noise “selfcorrelated” or “colored”. Data Communication, Lecture 9 26

Data Communication, Lecture 9 27

Data Communication, Lecture 9 28

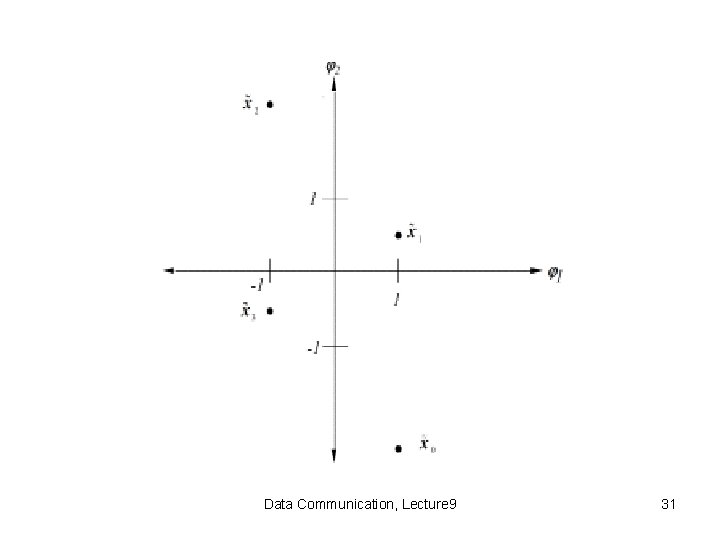
Example: QPSK with correlated Noise • One can compute that: Data Communication, Lecture 9 29

Data Communication, Lecture 9 30

Data Communication, Lecture 9 31

Thus, the optimum detector for this channel with self-correlated Gaussian noise has larger minimum distance than for the white noise case, illustrating the important fact that having correlated noise is sometimes advantageous. Data Communication, Lecture 9 32