Pairwise Sequence Alignment LESSON 32 HOMEWORK 2 Try

Pairwise Sequence Alignment LESSON 3(2)

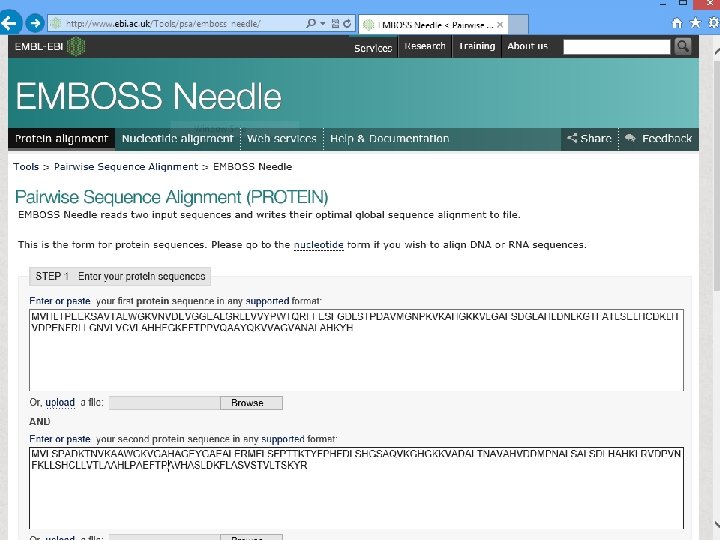
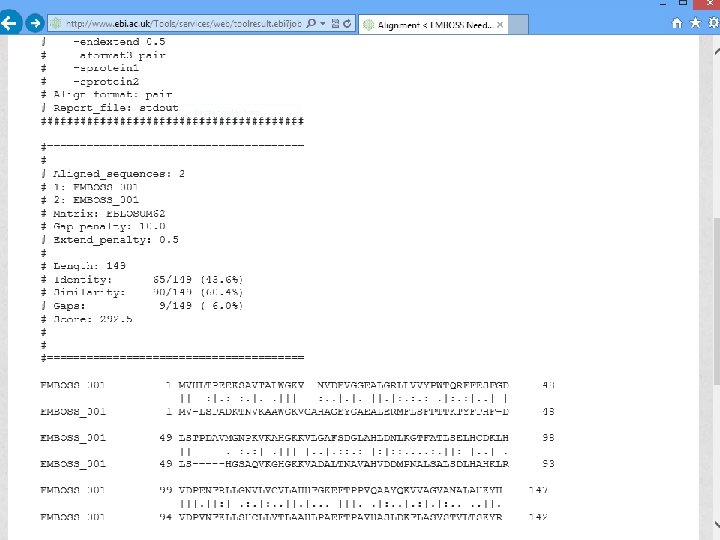
HOMEWORK 2 Try a pairwise alignment of human alpha and beta globin at the NCBI protein BLAST site, using the available matrices (PAM 30, PAM 70, PAM 250, BLOSUM 45, BLOSUM 62, BLOSUM 80). Which gives the highest bit score?

Protein alignment vs. DNA alignment Protein Alignment can be more Informative than DNA Alignment. BUT, ……

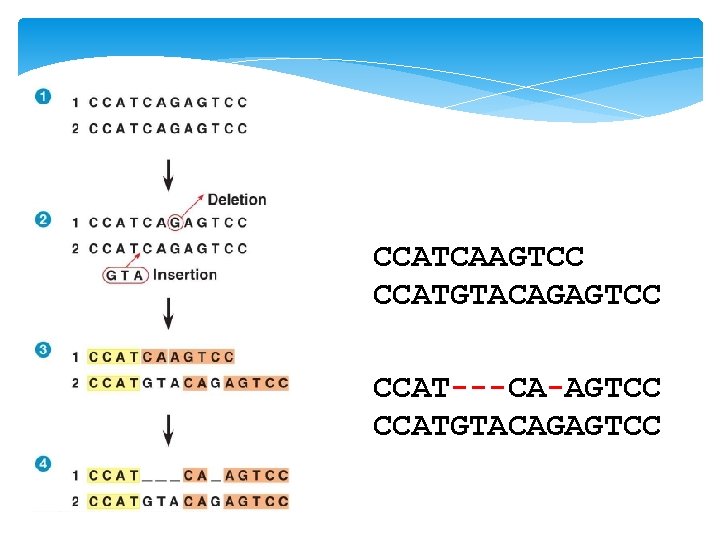
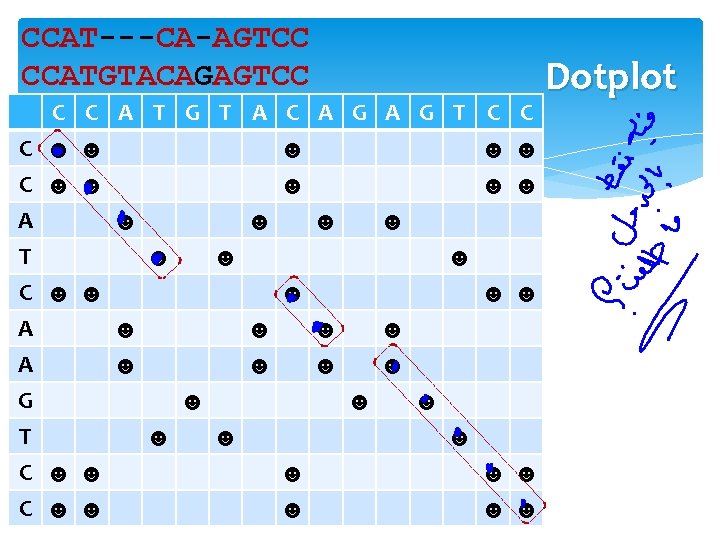
Percentage identity (% ID) 5/15 = 33 % CCATCAAGTCC CCATGTACAGAGTCC 11/15 = 73 % CCAT---CA-AGTCC CCATGTACAGAGTCC

CCATCAAGTCC CCATGTACAGAGTCC CCAT---CA-AGTCC CCATGTACAGAGTCC

Scoring Matrices CCATCAAGTCC CCATGTACAGA 1. Identity matrix (e. g. match=1 and mismatch=− 1) 2. Substitution matrix

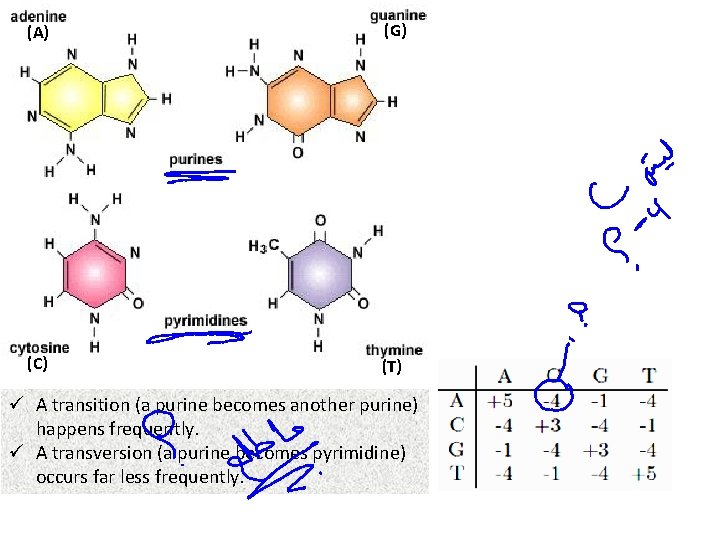
(A) (G) (C) (T) ü A transition (a purine becomes another purine) happens frequently. ü A transversion (a purine becomes pyrimidine) occurs far less frequently.

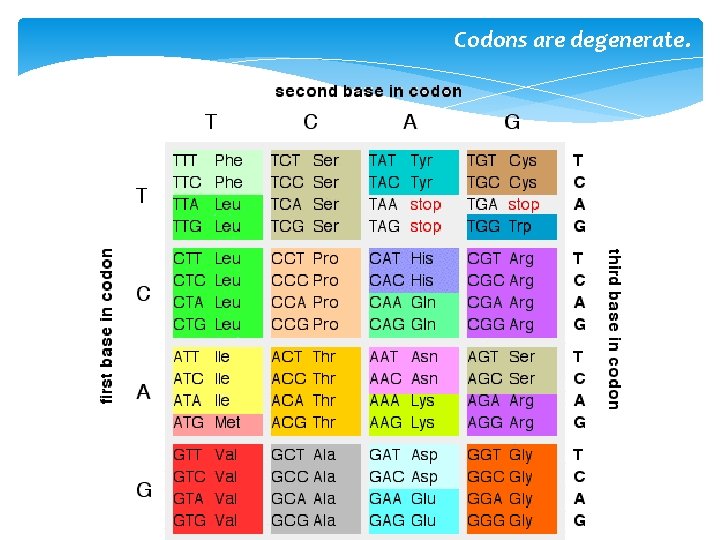
Codons are degenerate.

DNA Alignments are appropriate To confirm To study polymorphism To study non-coding regions of DNA

DNA Alignments for Finding regulatory elements in DNA sequences non-coding DNA ? full of regulatory elements give rise to the differences between organisms Each gene is associated with thousands of nucleotides of non-coding DNA.

Best alignment 1. Generate all possible gapped alignment. 2. Find the score for each. 3. Select the highest-scoring alignment. Time consuming 100 a. a : 1075 alignments Dynamic programming algorithm

Global Sequence Alignment: Needleman and Wunsch Algorithm

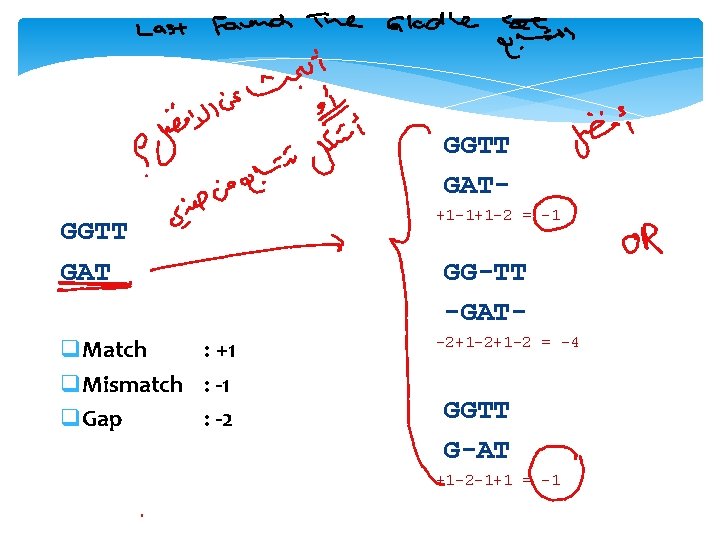
GGTT GAT q. Match : +1 q. Mismatch : -1 q. Gap : -2 +1 -1+1 -2 = -1 GG-TT -GAT-2+1 -2 = -4 GGTT G-AT +1 -2 -1+1 = -1

Alignment by Dynamic Programming Global Alignment Needleman & Wunsch (1970) used in major alignment software packages (e. g. the ALIGN tool in the FASTA package) Local Alignment Smith & Waterman Algorithm (1981)

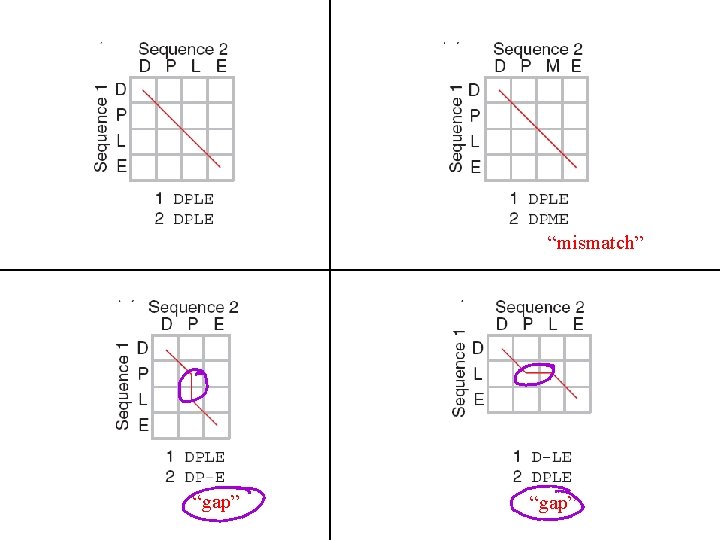
“mismatch” “gap”

Four possible outcomes in aligning two sequences 1 2 [1] identity (stay along a diagonal) [2] mismatch (stay along a diagonal) [3] gap in sequence 1 (move vertically!) [4] gap in sequence 2 (move horizontally!)

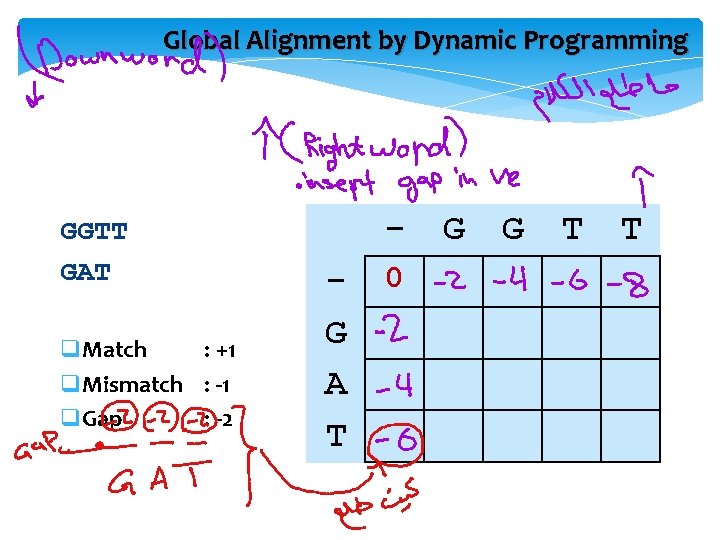
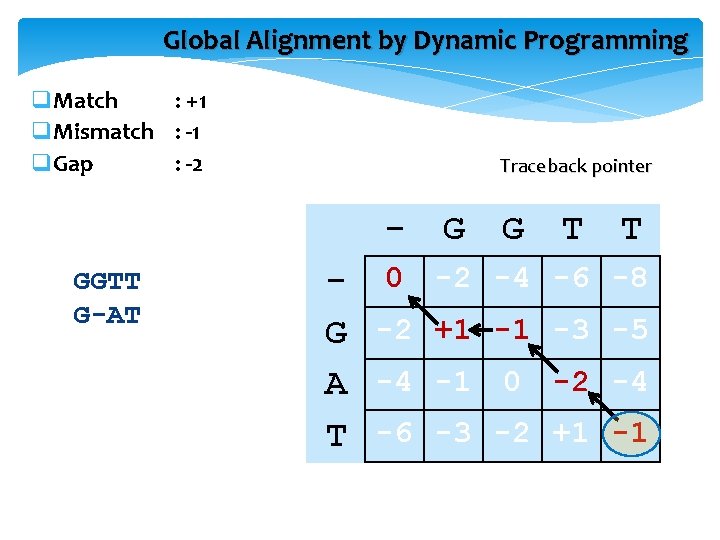
Global Alignment by Dynamic Programming GGTT GAT q. Match : +1 q. Mismatch : -1 q. Gap : -2 G A T 0 G G T T

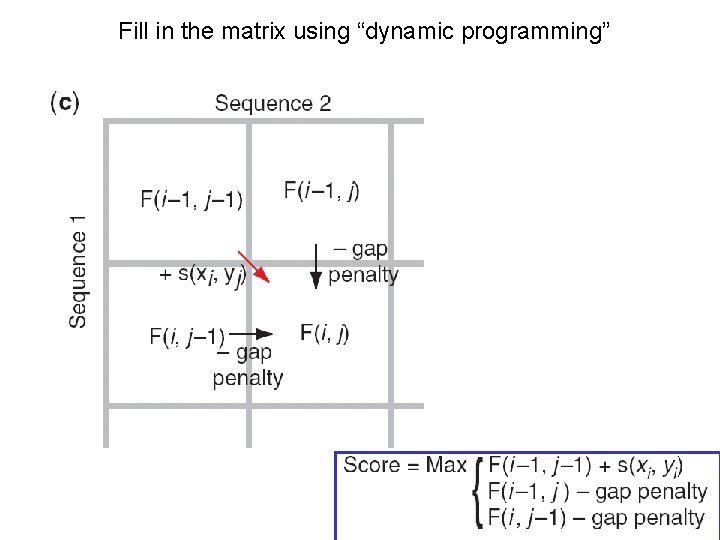
Fill in the matrix using “dynamic programming”

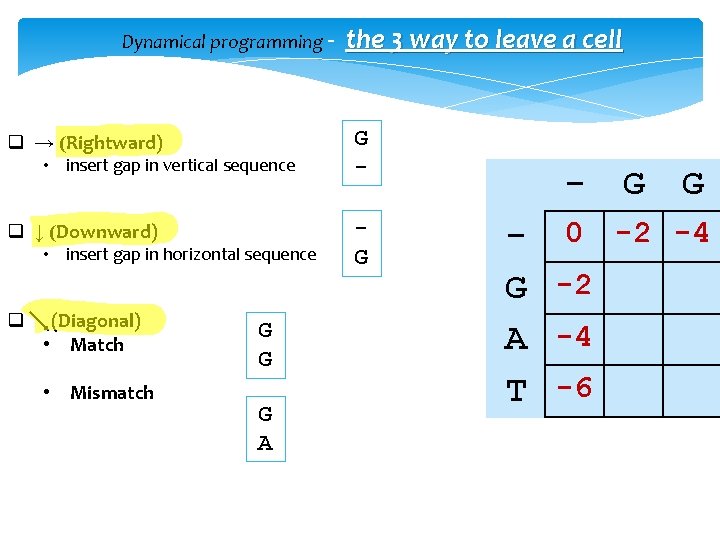
Dynamical programming - q → (Rightward) • insert gap in vertical sequence q ↓ (Downward) • insert gap in horizontal sequence q (Diagonal) • Match • Mismatch G G G A the 3 way to leave a cell G G - 0 -2 -4 G -2 A -4 T -6

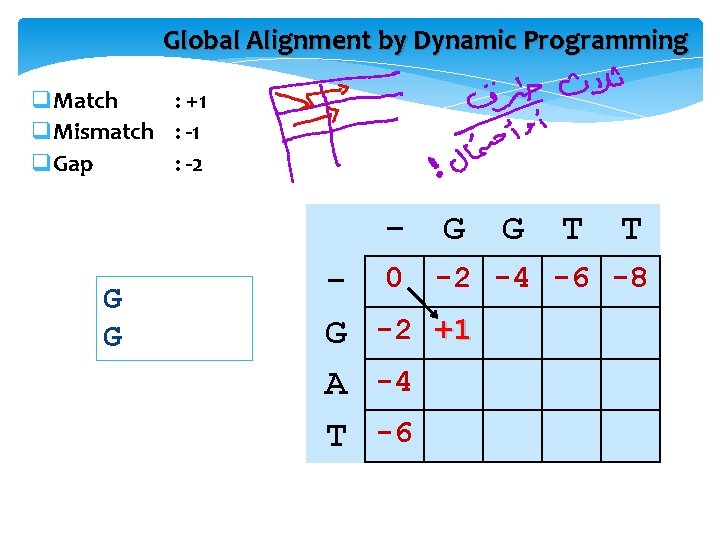
Global Alignment by Dynamic Programming q. Match : +1 q. Mismatch : -1 q. Gap : -2 G G T T - 0 -2 -4 -6 -8 G -2 +1 A -4 T -6

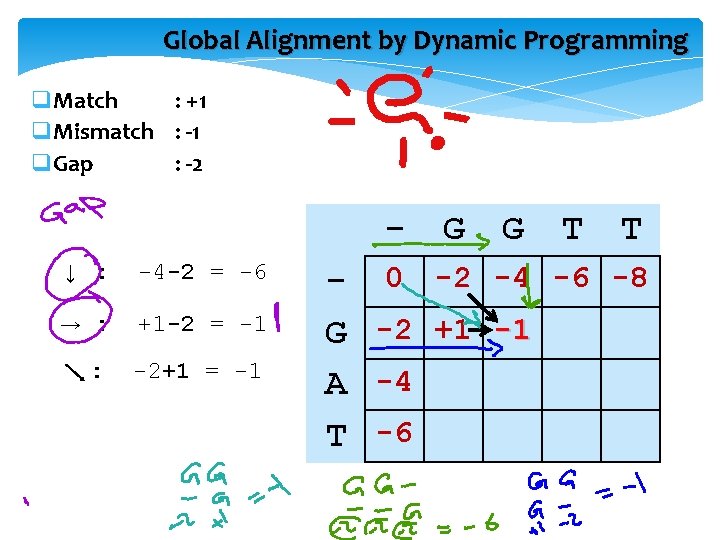
Global Alignment by Dynamic Programming q. Match : +1 q. Mismatch : -1 q. Gap : -2 ↓ : -4 -2 = -6 → : +1 -2 = -1 : -2+1 = -1 G G T T - 0 -2 -4 -6 -8 G -2 +1 -1 A -4 T -6

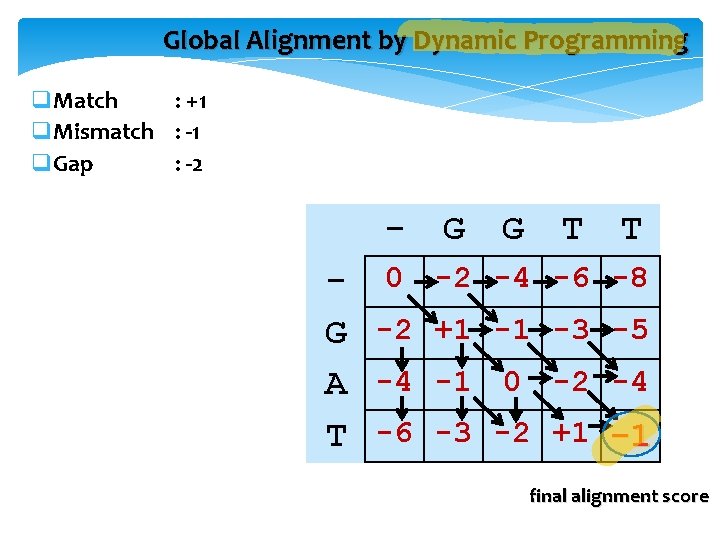
Global Alignment by Dynamic Programming q. Match : +1 q. Mismatch : -1 q. Gap : -2 - G G T - 0 -2 -4 G -2 +1 -1 A -4 -1 0 T -6 -3 -2 T -6 -8 -3 -5 -2 -4 +1 -1 final alignment score

Global Alignment by Dynamic Programming q. Match : +1 q. Mismatch : -1 q. Gap : -2 Traceback pointer GGTT G-AT G G - 0 -2 -4 G -2 +1 -1 A -4 -1 0 T -6 -3 -2 T T -6 -8 -3 -5 -2 -4 +1 -1

http: //www. ebi. ac. uk/Tools/emboss/

Local Alignment : Smith and Waterman Algorithm

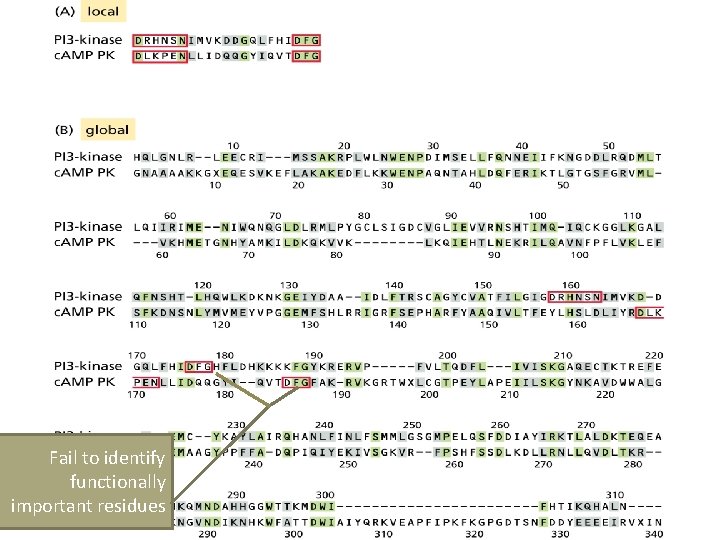
Fail to identify functionally important residues

Global vs. Local Global alignments o Comparing sequences over their entire length Local alignments o Comparing sequences with partial homology o Making high-quality alignments

Global alignment (top) includes matches ignored by local alignment (bottom) 15% identity 30% identity NP_824492, NP_337032

Domain

Local Alignments • Only aligns the most similar portions of sequences • To look for small parts of the sequences that are similar to each other. • searching for functionally related sequences • Programs for database searching • FASTA • BLAST

Alignments by Dynamic Programming S 1 = GCCCTAGCG S 2 = GCGCAATG q. Match : +1 q. Mismatch : -1 q. Gap : -2 • Needleman-Wunsch methods (Global Alignment) GCCCTAGCG I I I GCGC-AATG • Smith-Waterman methods (Local Alignment) GCCCTAGCG I I I GCGCAATG

Smith- Waterman methods • Dynamic programming algorithm for performing local sequence alignment • Traces only continue as long as the scores are positive. Whenever a score becomes negative it is set to 0. q diagonal q horizontal q vertical q 0. start again h h No values in the scoring matrix can be negative! H ≥ 0

Needleman-Wunsch methods (Global Alignment) Match : +1, Mismatch : -1, Gap : -2 GCCCTAGCG I I I GCGC-AATG

Smith-Waterman methods (Local Alignment) Match : +1, Mismatch : -1, Gap : -2 GCCCTAGCG I I I GCGCAATG

o The highest scoring cell does not need to be at the bottom right-hand corner, it could be anywhere in the matrix. o The backtracing procedure begins at the highest-scoring point in the matrix, and follows the arrows back until a 0 is reached. GCCCTAGCG I I I GCGCAATG