Pairwise Cardinality Networks Michael Codish and Moshe ZazonIvry

Pairwise Cardinality Networks Michael Codish and Moshe Zazon-Ivry Department of Computer Science Ben-Gurion University

Cardinality constraints in a nutshell �Satisfiability problems of the form: - conjunction of clauses - conjunction of constraints of the form � � is one of � Typically � �Applications: optimization problems, Max-Sat, scheduling problems, and more. �How to solve? �Dedicated solvers (SMT solvers) �Sat encoding � BDD-like structure � Sorting networks (unary ) � Networks of adders (binary)

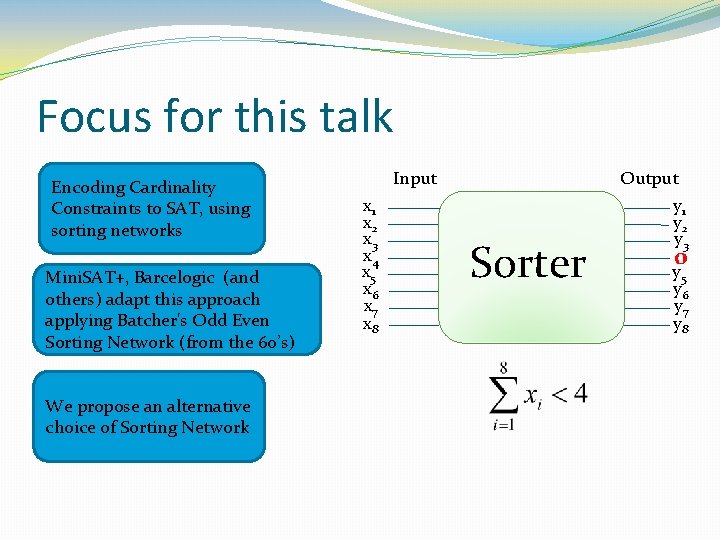
Focus for this talk Encoding Cardinality Constraints to SAT, using sorting networks Mini. SAT+, Barcelogic (and others) adapt this approach applying Batcher's Odd Even Sorting Network (from the 60’s) We propose an alternative choice of Sorting Network Input x 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 Output Sorter y 1 y 2 y 3 0 y 5 y 6 y 7 y 8

Outline of the talk �Sorting networks �Batcher’s Odd-Even (OE) Network �An Alternative - Parberry's Pairwise (PW) Network �Why an Alternative (I) - constraint propagation �Understanding OE vs. PW �Why an Alternative (II) - partial evaluation �Conclusion

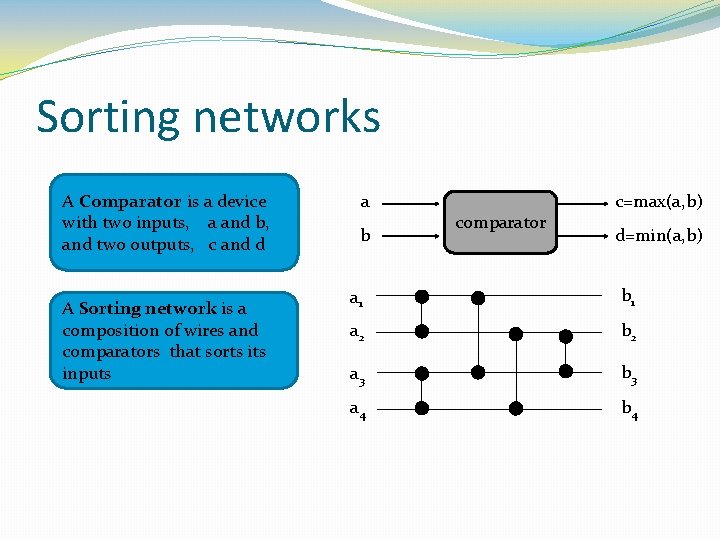
Sorting networks A Comparator is a device with two inputs, a and b, and two outputs, c and d A Sorting network is a composition of wires and comparators that sorts inputs a b comparator c=max(a, b) d=min(a, b) a 1 b 1 a 2 b 2 a 3 b 3 a 4 b 4

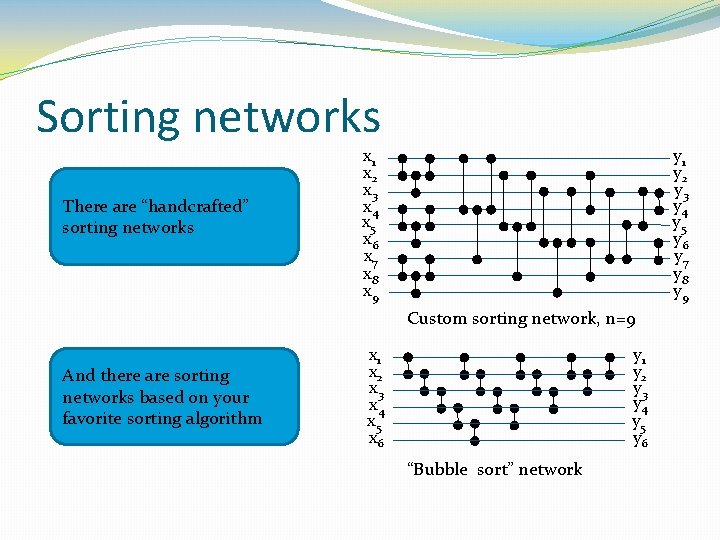
Sorting networks There are “handcrafted” sorting networks x 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 y 1 y 2 y 3 y 4 y 5 y 6 y 7 y 8 y 9 Custom sorting network, n=9 And there are sorting networks based on your favorite sorting algorithm x 1 x 2 x 3 x 4 x 5 x 6 y 1 y 2 y 3 y 4 y 5 y 6 “Bubble sort” network

Sat encoding - comparators a c b d The SAT encoding of a comparator(a, b, c, d) is:

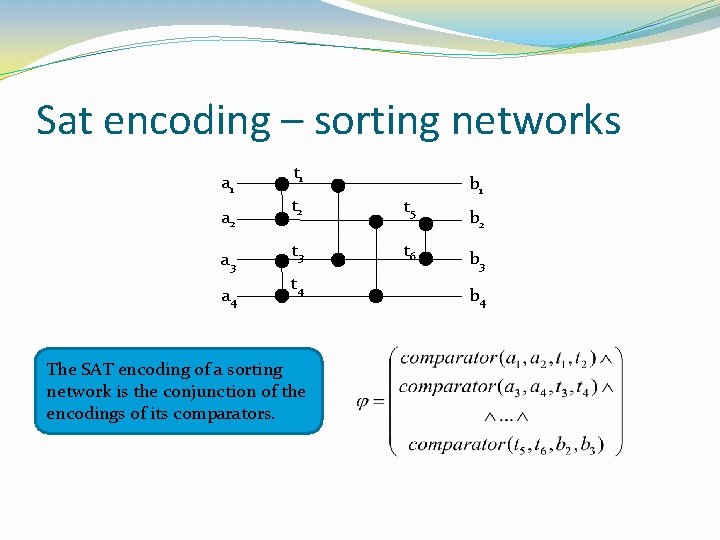
Sat encoding – sorting networks a 1 a 2 a 3 a 4 t 1 t 2 t 5 t 3 t 6 t 4 The SAT encoding of a sorting network is the conjunction of the encodings of its comparators. b 1 b 2 b 3 b 4

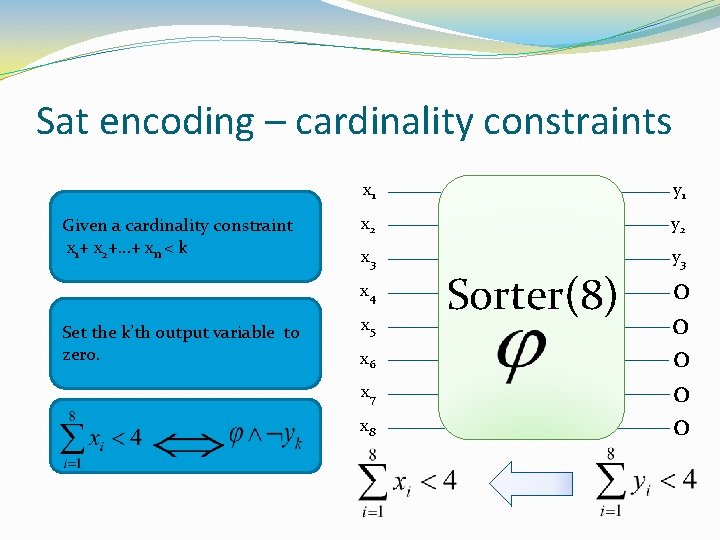
Sat encoding – cardinality constraints Given a cardinality constraint x 1+ x 2+…+ xn < k x 1 y 1 x 2 y 2 x 3 y 3 x 4 Set the k’th output variable to zero. x 5 x 6 x 7 x 8 Sorter(8) 0 0 0

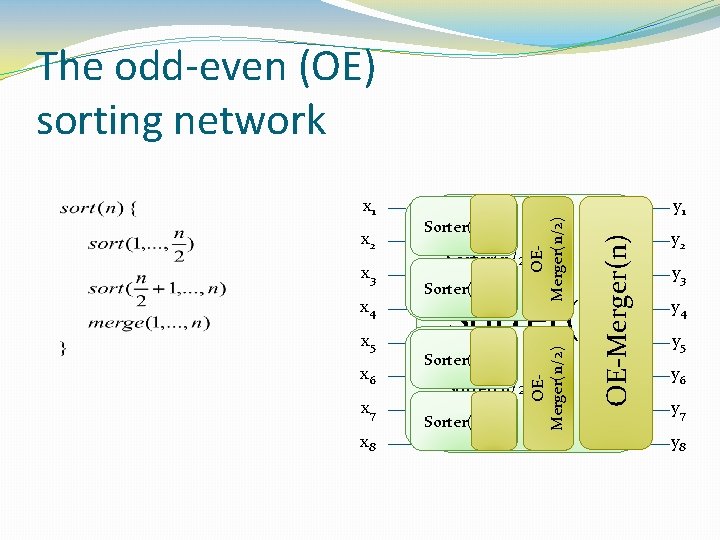
x 3 x 4 x 5 x 6 x 7 x 8 Sorter(n/4) Sorter(n/2) Sorter(n/4) y 1 OE-Merger(n) x 2 Sorter(n) Sorter(n/4) OEMerger(n/2) x 1 OEMerger(n/2) The odd-even (OE) sorting network Sorter(n/2) Sorter(n/4) y 2 y 3 y 4 y 5 y 6 y 7 y 8

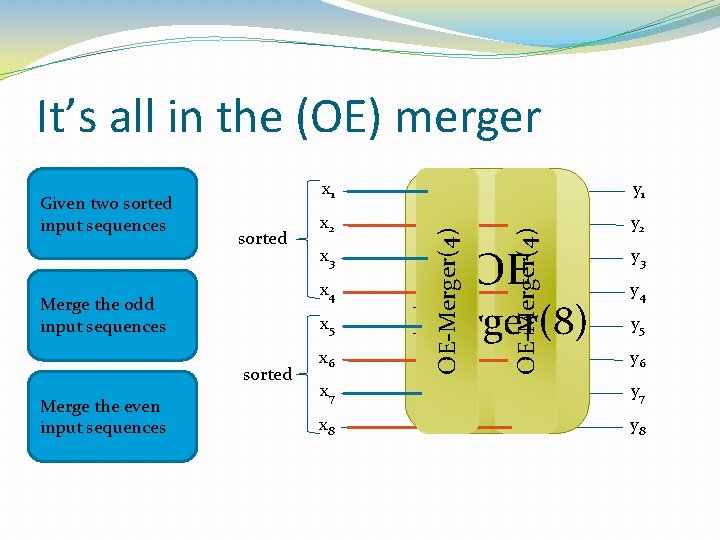
It’s all in the (OE) merger y 2 x 3 x 4 Merge the odd input sequences x 5 sorted Merge the even input sequences x 2 x 6 OE-Merger(4) sorted y 1 OE-Merger(4) Given two sorted input sequences x 1 OE Merger(8) y 3 y 4 y 5 y 6 x 7 y 7 x 8 y 8

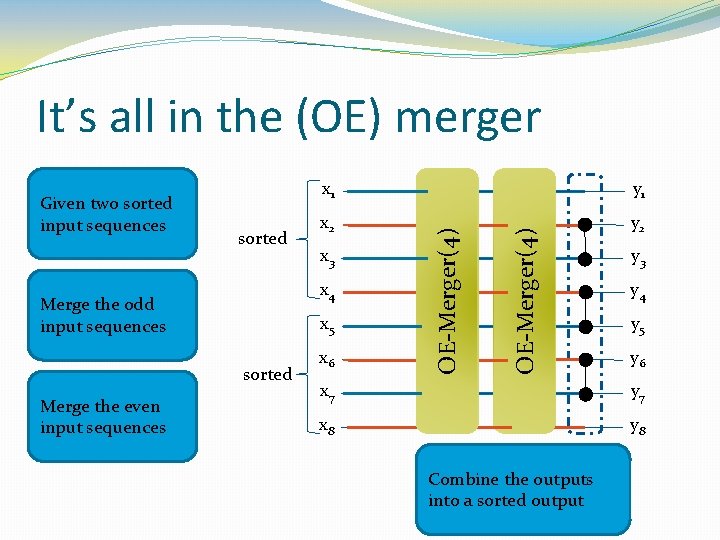
It’s all in the (OE) merger y 2 x 3 x 4 Merge the odd input sequences x 5 sorted Merge the even input sequences x 2 x 6 OE-Merger(4) sorted y 1 OE-Merger(4) Given two sorted input sequences x 1 y 3 y 4 y 5 y 6 x 7 y 7 x 8 y 8 Combine the outputs into a sorted output

And Then There Was … Ian Parberry devised the pairwise (PW) sorting network in 1992 It has the exact same size & depth as the OE sorting network, but it is not isomorphic , … Ian Parberry “The value of the pairwise sorting network is not that it is superior to the odd-even sorting network in any sense, but that it is the first serious rival to appear in over 20 years”

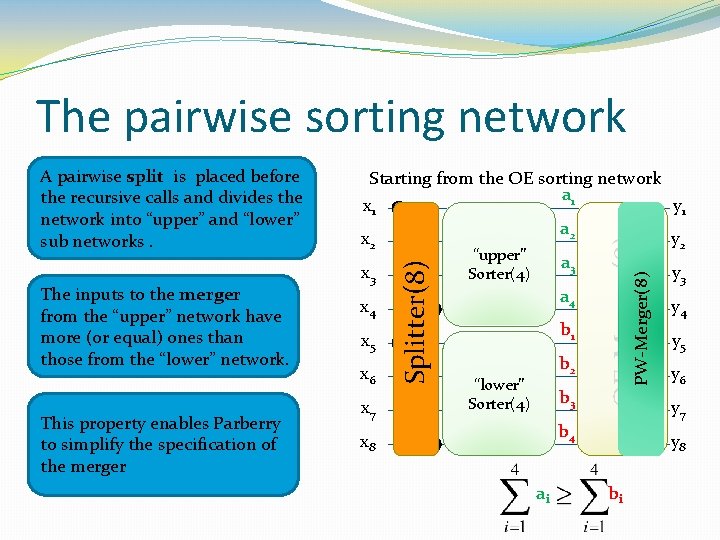
The pairwise sorting network This property enables Parberry to simplify the specification of the merger OE-Merger(8) PW-Merger(8) The inputs to the merger from the “upper” network have more (or equal) ones than those from the “lower” network. Starting from the OE sorting network a 1 x 1 a 2 x 2 “upper” a 3 x 3 Sorter(4) a 4 x 4 b 1 x 5 b 2 x 6 “lower” b 3 Sorter(4) x 7 b 4 x 8 Splitter(8) A pairwise split is placed before the recursive calls and divides the network into “upper” and “lower” sub networks. ai bi y 1 y 2 y 3 y 4 y 5 y 6 y 7 y 8

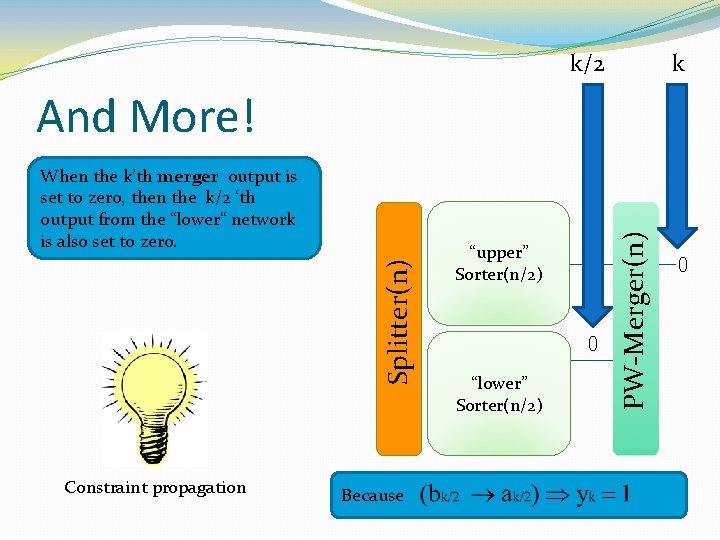
k/2 k Splitter(n) When the k’th merger output is set to zero, then the k/2 ‘th output from the “lower“ network is also set to zero. Constraint propagation Because “upper” Sorter(n/2) 0 “lower” Sorter(n/2) PW-Merger(n) And More! 0

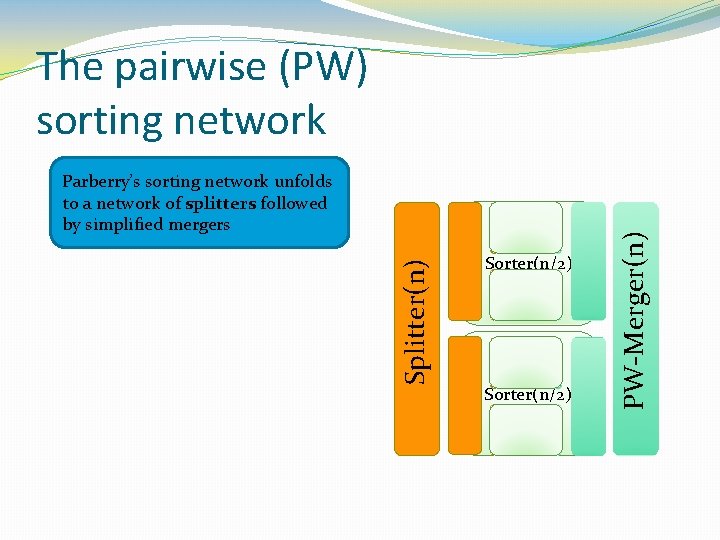
Splitter(n) Parberry’s sorting network unfolds to a network of splitters followed by simplified mergers Sorter(n/2) PW-Merger(n) The pairwise (PW) sorting network

What is the pairwise merger? The pairwise merger is constructed by layers of comparators Each layer reduces the “amplitude” of the sequence by half Check the Parberry paper, it’s a bit technical x 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 x 11 x 12 x 13 x 14 x 15 x 16 y 1 y 2 y 3 y 4 y 5 y 6 y 7 y 8 y 9 y 10 y 11 y 12 y 13 y 14 y 15 y 16

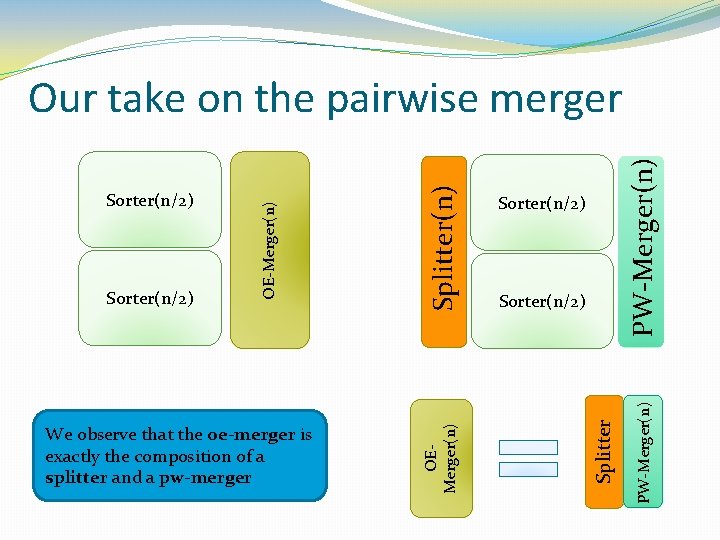
PW-Merger(n) Sorter(n/2) Splitter We observe that the oe-merger is exactly the composition of a splitter and a pw-merger Splitter(n) Sorter(n/2) OEMerger(n) Sorter(n/2) OE-Merger(n) Our take on the pairwise merger

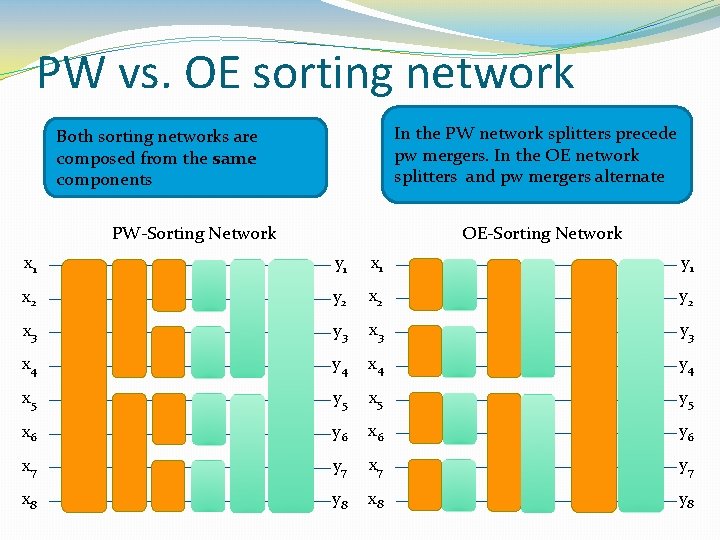
PW vs. OE sorting network In the PW network splitters precede pw mergers. In the OE network splitters and pw mergers alternate Both sorting networks are composed from the same components OE-Sorting Network PW-Sorting Network x 1 y 1 x 2 y 2 x 3 y 3 x 4 y 4 x 5 y 5 x 6 y 6 x 7 y 7 x 8 y 8

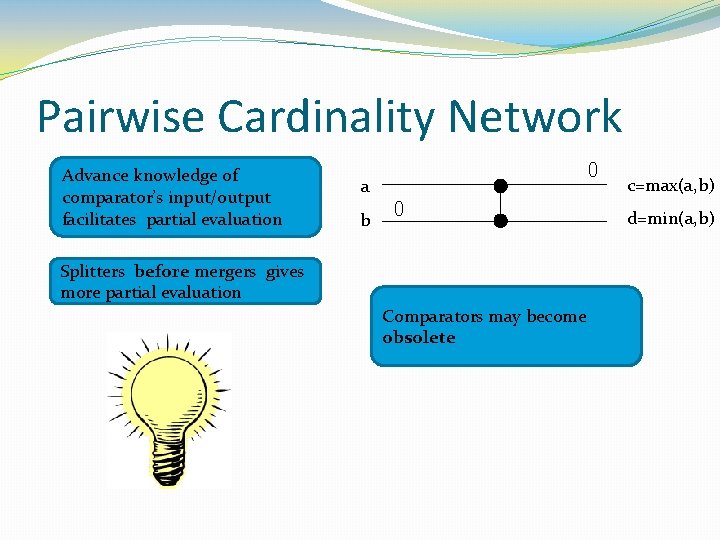
Pairwise Cardinality Network Advance knowledge of comparator’s input/output facilitates partial evaluation a b 0 0 Splitters before mergers gives more partial evaluation Comparators may become obsolete c=max(a, b) d=min(a, b)

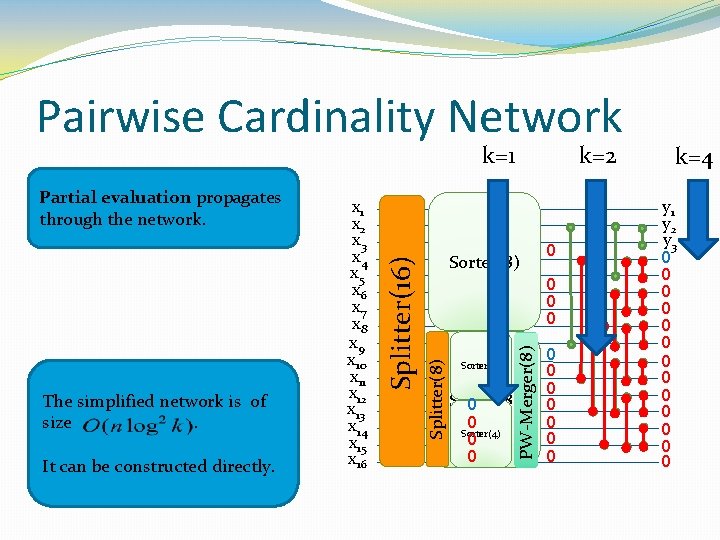
Pairwise Cardinality Network It can be constructed directly. Sorter(8) k=2 0 0 Sorter(4) PW-Merger(8) The simplified network is of size. x 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 x 11 x 12 x 13 x 14 x 15 x 16 Splitter(8) Partial evaluation propagates through the network. Splitter(16) k=1 Sorter(8) 0 0 Sorter(4) 0 0 0 0 0 k=4 y 1 y 2 y 3 0 0 0 0

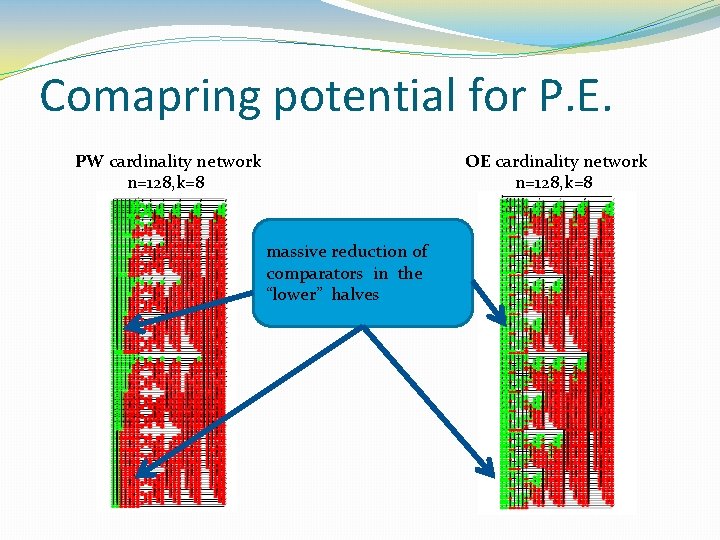
Comapring potential for P. E. PW cardinality network n=128, k=8 OE cardinality network n=128, k=8 massive reduction of comparators in the “lower” halves

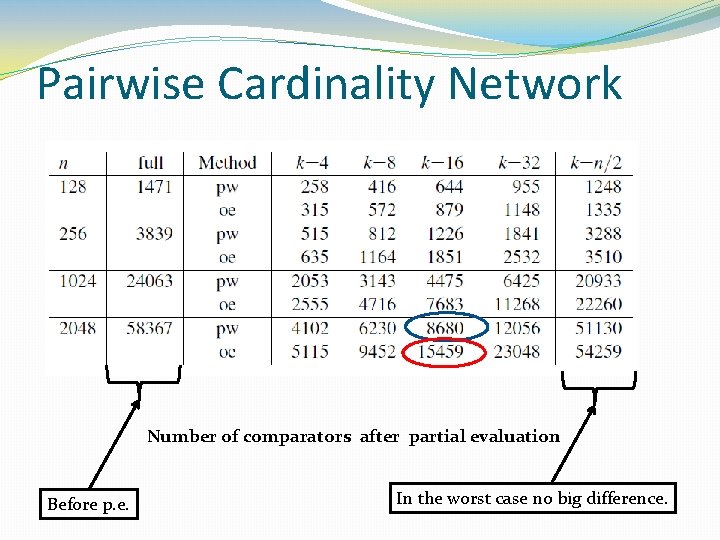
Pairwise Cardinality Network Number of comparators after partial evaluation Before p. e. In the worst case no big difference.

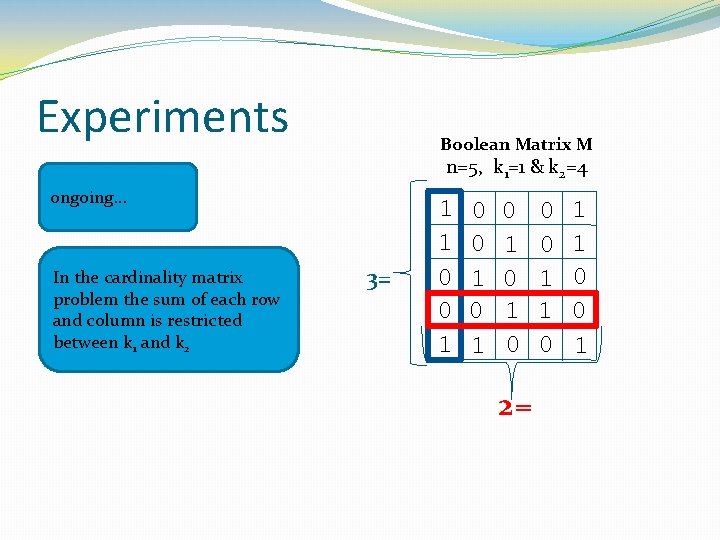
Experiments Boolean Matrix M n=5, k 1=1 & k 2=4 ongoing. . . In the cardinality matrix problem the sum of each row and column is restricted between k 1 and k 2 3= 1 1 0 0 1 0 1 0 2= 0 0 1 1 0 0 1

Experiments For a Boolean Matrix with n=100 Cardinality Network proposed by Asin etal [1]

Conclusion �Propose cardinality networks based on pairwise sorting networks instead of odd-even networks �Better constraint propagation �Better partial evaluation �Improve understanding on the relation between pairwise and odd-even networ ks �Pairwise Networks are better for cardinality constraints and should be considered in tools (Mini. SAT+, etc).