Page 146 Chapter 3 True False Questions 1












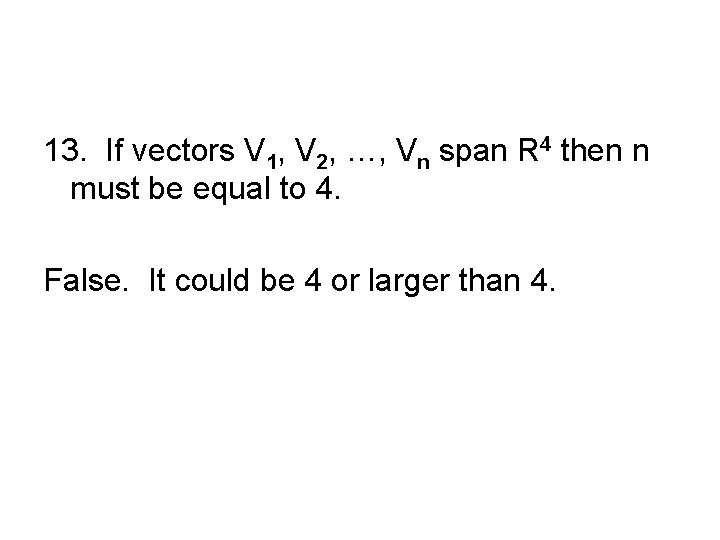


























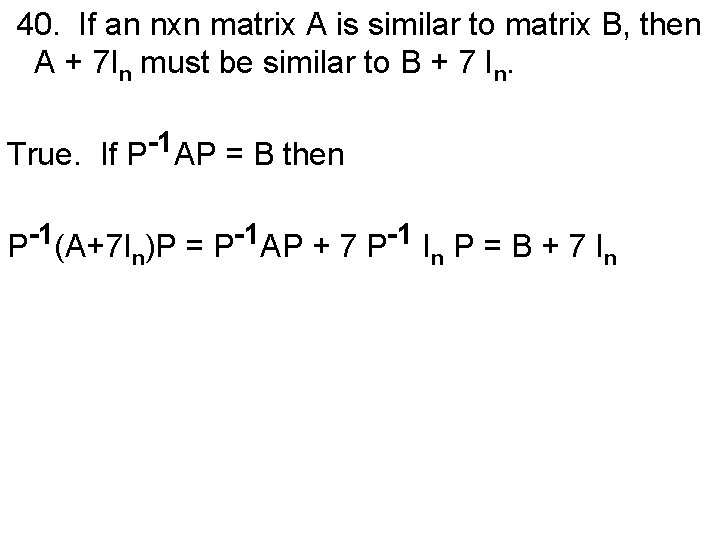











- Slides: 51

Page 146 Chapter 3 True False Questions. 1. The image of a 3 x 4 matrix is a subspace of R 4? False. It is a subspace of R 3.

2. The span of vectors V 1, V 2, …, Vn consists of all linear combinations of vectors V 1, V 2, …, Vn. True. That is the definition of the span.

3. If V 1, V 2, …, Vn are linearly independent vectors in Rn, then they must form a basis of Rn. True: n linearly independent vectors in a space of dimension n form a basis.

4. There is a 5 x 4 matrix whose image consists of all of R 5. False. It takes at least 5 vectors to span all of R 5.

5. The kernel of any invertible matrix consists of the zero vector only. True. AX = 0 implies X = 0 when A is invertible.

6. The identity matrix In is similar to all invertible nxn matrices. False. The identity matrix is similar only to itself. A-1 I A = I for all invertible matrices A.

7. If 2 U + 3 V + 4 W = 5 U + 6 V + 7 W, then vectors U, V, W must be linearly dependent. True. In fact 3 U+3 V+3 W = 0.

8. The column vectors of a 5 x 4 matrix must be linearly dependent. False. |1 0 0 0| |0 1 0 0| |0 0 1 0| |0 0 0 1| |0 0 0 0| is an example where they are linearly independent.

9. If V 1, V 2, …, Vn and W 1, W 2, …, Wm are any two bases of a subspace V of R 10, then n must equal m. True. Any two bases of the same vector space have the same number of vectors.

10. If A is a 5 x 6 matrix of rank 4, then the nullity of A is 1. False. The rank plus the nullity is the number of columns. Thus the nullity would be 2.

11. If the kernel of a matrix A consists of the zero vector only, then the column vectors of A must be linearly independent. True. Since the kernel is zero, the columns of A must be linearly independent.

12. If the image of an nxn matrix A is all of Rn, then A must be invertible. True. Since the columns span Rn , the matrix must have a right inverse. Since it is square, it must be invertible.
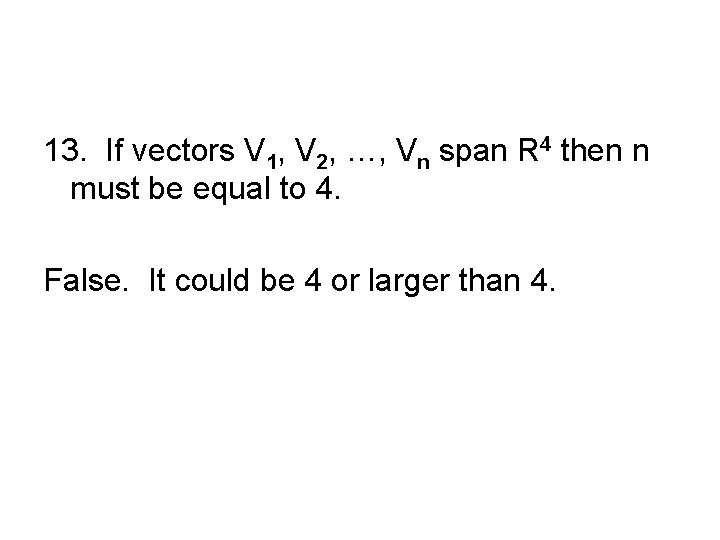
13. If vectors V 1, V 2, …, Vn span R 4 then n must be equal to 4. False. It could be 4 or larger than 4.

14. If vectors U, V, and W are in a subspace V of Rn, then 2 U – 3 V + 4 W must be in V as well. True. A subspace is closed under addition and scalar multiplication.

15. If matrix A is similar to matrix B, and B is similar to C, then C must be similar to A. True. P-1 AP = B Q-1 BQ = C Q-1 P-1 APQ = C A = PQCQ-1 P-1 A = (Q-1 P-1)-1 C (Q-1 P-1)

16. If a subspace V of Rn contains none of the standard vectors E 1, E 2, …, En, then V consists of the zero vector only. |c| False. The space | c | of R 3 is a |c| counter example.

17. If vectors V 1, V 2, V 3, V 4 are linearly independent, then vectors V 1, V 2, V 3 must be linearly independent as well. True. Any dependence relation among V 1, V 2, V 3 can be made into a dependence relation for V 1, V 2, V 3, V 4 by adding a zero coefficient to V 4.

| a | 18. The vectors of the form | b | | 0 | | a | (where a and b are arbitrary real numbers) form a subspace of R 4. True. This is closed under addition and scalar multiplication.

19. Matrix | 1 0 | is similar to | 0 1 |. | 0 -1 | |1 0| -1 True. |1/2 -1/2 | | 1 0| |1/2 -1/2 | = | 0 1 | |1/2 | | 0 -1| |1/2 1/2| |10|

| 1 | |2| |3| 20. Vectors | 0 |, | 1 |, | 2 | form a basis of R 3. | 0 | |0| |1| | 1 | | 2 | | 3 | |a+2 b+3 c| True. a| 0 |+b| 1 |+c| 2 | = | b+2 c | |0| |1| | c | For the dependence relation to equal zero, we must have c = 0, then b=0, then a=0. Thus the three vectors are linearly independent and must be a basis of R 3.

21. Matrix | 0 1 | is similar to | 0 0 |. |0 0| | 0 1 | False. The first matrix squares to zero. The second matrix does not square to zero. They cannot be similar.

22. These vectors are linearly independent. |1| |2| |3| |4| |5| |6| |7| |8| |9| |8| |7| |6| |5| |4| |3| |2| |1| |0| |-1 | |-2 | False. They are five vectors in a space of dimension 4. They must be linearly dependent.

23. If a subspace V of R 3 contains the standard vectors E 1, E 2, E 3, then V must be R 3. True. Clearly everything is a linear combination of E 1, E 2, and E 3.

24. If a 2 x 2 matrix P represents the orthogonal projection onto a line in R 2, then P must be similar to matrix | 1 0 |. | 0 0| True. Use one basis vector along the line things are projected onto, and put the other basis vector along the line perpendicular to the first.

25. If A and B are nxn matrices, and vector V is in the kernel of both A and B, then V must be in the kernel of matrix AB as well. True. In fact we did not even need V to be in the kernel of A. If V is in the kernel of B, then V is in the kernel of AB.

26. If two nonzero vectors are linearly dependent, then each of them is a scalar multiple of the other. True. The dependence relation a. V+b. W = 0 has to have both a and b nonzero. Then V = -b/a W and W = -a/b V.

27. If V 1, V 2, V 3 are any three vectors in R 3, then there must be a linear transformation T from R 3 to R 3 such that T(V 1) = E 1, T(V 2) = E 2, and T(V 3) = E 3. False. You can do this when they are independent. You cannot do it when they are dependent.

28. If vectors U, V, W are linearly dependent, then vector W must be a linear combination of U and V. False. Let U = V = 0 and W = E 3.

29. If A and B are invertible nxn matrices, then AB is similar to BA. True. A-1(AB)A = BA

30. If A is an invertible nxn matrix, then the -1 kernels of A and A must be equal. True. In fact the kernels of A and A-1 are both just 0.

31. If V is any three-dimensional subspace of R 5 then V has infinitely many bases. True. If V 1, V 2, V 3 is one basis, then V 1+k. V 2, V 3 is another basis for each integer k.

32. Matrix In is similar to 2 In. False. In is similar to only itself.

33. If AB = 0 for two 2 x 2 matrices A and B, then BA must be the zero matrix as well. False. |0 0| |1 0| |0 0| = | 0 0 | |0 1| | 0 0 | |0 0| |0 1| |0 0| = | 0 0 | |1 0| | 1 0 |

34. If A and B are nxn matrices, and V is in the image of both A and B, then V must be in the image of matrix A+B as well. False. Consider B = -A. Then A+B = 0 yet A and B have the same image.

35. If V and W are subspaces of Rn, then their union Vu. W must be a subspace of Rn as well. False. V = | c | |0| W = | 0 |. |d| Then Vu. W is not closed under addition since | c | is not in the union. |d|

36. If the kernel of a 5 x 4 matrix A consists of the zero vector only and if AV = AW for two vectors V and W in R 4, then vectors V and W must be equal. True. Since A(V-W) = 0, V-W = 0 and so V=W.

37. If V 1, V 2, …, Vn and W 1, W 2, …, Wn are two bases of Rn, then there is a linear transformation T from Rn to Rn such that T(V 1) = W 1, T(V 2) = W 2, …, T(Vn) = Wn. True. You can map a basis anywhere.

38. If matrix A represents a rotation through Pi/2 and matrix B rotation through Pi/4, then A is similar to B. False. A = | 0 -1 | | 1 0| B = | 1/Sqrt[2] -1/Sqrt[2] | | 1/Sqrt[2] | A 4 = I and B 4 =/= I. They cannot be similar.

39. R 2 is a subspace of R 3. False. There are subspaces of R 3 of dimension 2, but the vectors in them are all three tuples, not 2 tuples.
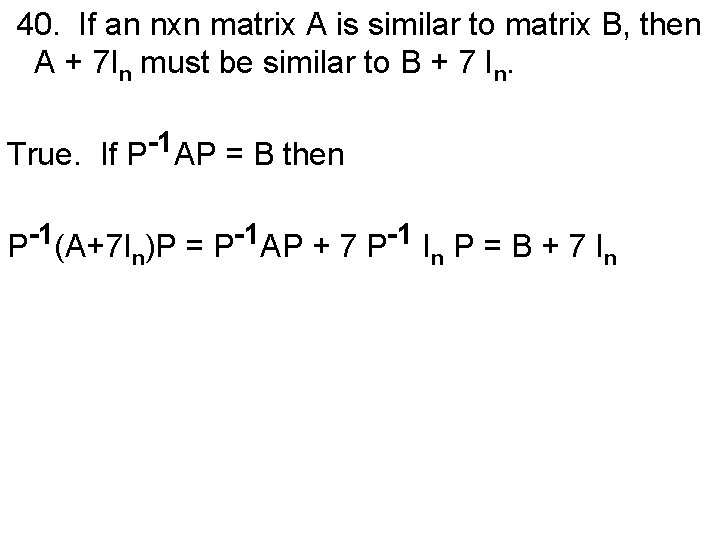
40. If an nxn matrix A is similar to matrix B, then A + 7 In must be similar to B + 7 In. True. If P-1 AP = B then P-1(A+7 In)P = P-1 AP + 7 P-1 In P = B + 7 In

41. There is a 2 x 2 matrix A such that im(A) = ker(A). True. | 0 1 | is one such matrix. |00 |

42. If two nxn matrices A and B have the same rank, then they must be similar. False. | 1 0 | and | 0 1 | both have rank |0 0| |00| one, but are not similar.

43. If A is similar to B, and A is invertible, then B must be invertible as well. True. If P-1 A P = B then P-1 A-1 P = B-1

44. If A 2 = 0 for a 10 x 10 matrix A, then the inequality rank(A) <= 5 must hold. True. 10 = rank(A) + nullity(A) Since A is contained in the null space of A, 10 >= 2 rank(A). So rank(A) <= 5.

45. For every subspace V of R 3 there is a 3 x 3 matrix A such that V = im(A). True. Just pick 3 vectors which span V. Use these as the columns of the matrix.

46. There is a nonzero 2 x 2 matrix A that is similar to 2 A. True. | 2 0| |01| |½ 0| =|0 2| | 0 1| |00| |0 1| | 0 0|

47. If the 2 x 2 matrix R represents the reflection across a line in R 2, then R must be similar to the matrix | 0 1 |. | 1 0 | True. Use the basis | / _____|/_______ | |

48. If A is similar to B, then there is one and only -1 one invertible matrix S such that S A S = B. False. (A-1 S)-1 A (A-1 S) will also work.

49. If the kernel of a 5 x 4 matrix A consists of the zero vector alone, and if AB = AC for two 4 x 5 matrices B and C, then the matrices B and C must be equal. True. A(B-C) = 0 so B-C = 0 and so B=C.

50. If A is any nxn matrix such that A 2 = A, then the image of A and the kernel of A have only the zero vector in common. True. If A(AV) = 0, that is, if AV is in the image of A and also in the kernel of A, then 0 = A 2 V = AV.

51. There is a 2 x 2 matrix A such that A 2 =/= 0 and A 3 = 0. False. If A 2 V =/= 0, and A 3 V = 0, then V, A 2 V must be linearly independent. This is impossible in R 2.
 True or false true or false
True or false true or false True or false mla requires a title page
True or false mla requires a title page There are four seasons all over the world true or false
There are four seasons all over the world true or false True or false questions about leadership
True or false questions about leadership True or false science questions
True or false science questions Psychology true or false
Psychology true or false True or false nutrition questions
True or false nutrition questions Cells are the basic unit of life true or false
Cells are the basic unit of life true or false True or false questions on research methodology
True or false questions on research methodology Finance true/false questions
Finance true/false questions The ten commandments of satan
The ten commandments of satan How to answer true or false questions
How to answer true or false questions Bird true or false questions
Bird true or false questions How to answer true or false questions
How to answer true or false questions True and false questions about smoking
True and false questions about smoking True or false jeopardy questions
True or false jeopardy questions Chapter 41 telephone techniques true or false
Chapter 41 telephone techniques true or false Accounting chapter 14 true and false
Accounting chapter 14 true and false Test 11a accounting
Test 11a accounting Chapter 37 vital signs and measurements true or false
Chapter 37 vital signs and measurements true or false Chapter 41 telephone techniques true or false
Chapter 41 telephone techniques true or false Chapter 3 true or false
Chapter 3 true or false Chapter 2 jesus christ true god and true man
Chapter 2 jesus christ true god and true man If ? true : false
If ? true : false Longitudinal wave vs transverse wave
Longitudinal wave vs transverse wave Groundwater true/false quiz answers
Groundwater true/false quiz answers Which of these statements is false
Which of these statements is false False and true vocal cords
False and true vocal cords Parallelogram properties
Parallelogram properties Percent increase and decrease maze answer key
Percent increase and decrease maze answer key Difference between true ribs and false ribs
Difference between true ribs and false ribs Contingency measures during workplace accidents
Contingency measures during workplace accidents Logical operators truth table
Logical operators truth table Radiation travels in straight lines
Radiation travels in straight lines Identify each statement as either true or false.
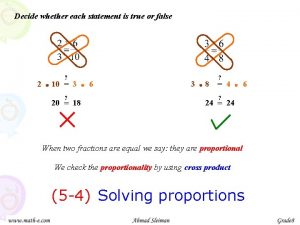
Identify each statement as either true or false. Decide whether each statement is true or false
Decide whether each statement is true or false Business letter quiz
Business letter quiz Body language is universal true or false
Body language is universal true or false The narrator was brought up mainly in
The narrator was brought up mainly in Flour is always made of wheat. true false
Flour is always made of wheat. true false True/false: there are ten spanish-speaking countries.
True/false: there are ten spanish-speaking countries. Tipe data bahasa pascal
Tipe data bahasa pascal Yang termasuk tipe data perbandingan adalah …
Yang termasuk tipe data perbandingan adalah … Belong images
Belong images Geometry chapter 6 review
Geometry chapter 6 review Quiz on road safety with answer
Quiz on road safety with answer Wanted: a just right government
Wanted: a just right government Dance is always done to music true or false
Dance is always done to music true or false Truemaps
Truemaps To kill a mockingbird jeopardy part 1
To kill a mockingbird jeopardy part 1 Which sentence diagram shows a compound sentence?
Which sentence diagram shows a compound sentence? Sexual harassment quiz
Sexual harassment quiz