Packing to fewer dimensions Paolo Ferragina Dipartimento di

Packing to fewer dimensions Paolo Ferragina Dipartimento di Informatica Università di Pisa

Speeding up cosine computation n What if we could take our vectors and “pack” them into fewer dimensions (say 50, 000 100) while preserving distances? n n n Now, O(nm) to compute cos(d, q) for all n docs Then, O(km+kn) where k << n, m Two methods: n n “Latent semantic indexing” Random projection

Briefly n LSI is data-dependent n n Create a k-dim subspace by eliminating redundant axes Pull together “related” axes – hopefully n n car and automobile What about polysemy ? Random projection is data-independent n Choose a k-dim subspace that guarantees good stretching properties with high probability between any pair of points.

Sec. 18. 4 Latent Semantic Indexing courtesy of Susan Dumais

Notions from linear algebra n n n Matrix A, vector v Matrix transpose (At) Matrix product Rank Eigenvalues l and eigenvector v: Av = lv Example

Overview of LSI n Pre-process docs using a technique from linear algebra called Singular Value Decomposition n Create a new (smaller) vector space n Queries handled (faster) in this new space

Singular-Value Decomposition n Recall m n matrix of terms docs, A. n A has rank r m, n Define term-term correlation matrix T=AAt n T is a square, symmetric m m matrix n Let U be m r matrix of r eigenvectors of T Define doc-doc correlation matrix D=At. A n D is a square, symmetric n n matrix n Let V be n r matrix of r eigenvectors of D

A’s decomposition n n Given U (for T, m r) and V (for D, n r) formed by orthonormal columns (unit dot-product) It turns out that n A = U S Vt Where S is a diagonal matrix with the eigenvalues of T=AAt in decreasing order. m n A = m r U r r S r n Vt

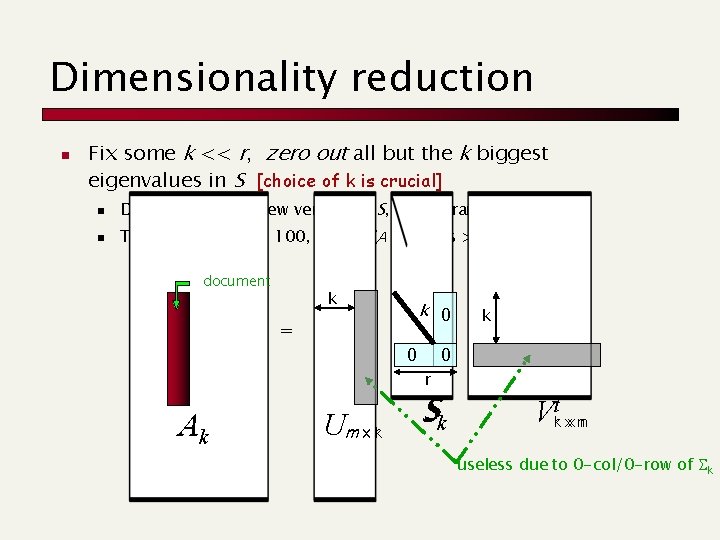
Dimensionality reduction n Fix some k << r, zero out all but the k biggest eigenvalues in S [choice of k is crucial] n n Denote by Sk this new version of S, having rank k Typically k is about 100, while r (A’s rank) is > 10, 000 document k k 0 = 0 k 0 r Ak Um x kr Sk Vkrt xx nn useless due to 0 -col/0 -row of Sk

A running example

A running example

A running example

Guarantee n Ak is a pretty good approximation to A: n n Relative distances are (approximately) preserved Of all m n matrices of rank k, Ak is the best approximation to A wrt the following measures: n min. B, rank(B)=k ||A-B||2 = ||A-Ak||2 = sk+1 n min. B, rank(B)=k ||A-B||F 2 = ||A-Ak||F 2 = sk+12+ sk+22+. . . + sr 2 n Frobenius norm ||A||F 2 = s 12+ s 22+. . . + sr 2

Reduction n Xk = S k Vt n n n U, V are formed by orthonormal eigenvectors of the matrices D, T is the doc-matrix k x n, hence reduced to k dim Since we are interested in doc/q correlation, we consider: n D=At A =(U S V t)t (U S V t) = (S V t)t (S V t) Approx S with Sk, thus get At A Xkt Xk (both are n x n matr. ) We use Xk to define how to project A and Q: n Xk = Sk Vk t Xk = Ukt A (using the def of SVD of A) In fact Xk plays the role of A, and hence its columns are the projected docs n Similarly Q can be interpreted as a new col of A and thus it is enough to multiply Ukt times Q to get the projected query, O(km) time

Which are the concepts ? n c-th concept = c-th col of Uk n (which is m x k) Uk[i][c] = strength of association between c-th concept and i-th term n Vtk[c][j] = strength of association between c-th concept and j-th document n Projected document: d’j = Utk dj n n d’j [c] = strenght of concept c in dj Projected query: q’ = Utk q n q’[c] = strenght of concept c in q

Random Projections Paolo Ferragina Dipartimento di Informatica Università di Pisa Slides only !

An interesting math result Lemma (Johnson-Linderstrauss, ‘ 82) Let P be a set of n distinct points in m-dimensions. Given e > 0, there exists a function f : P IRk such that for every pair of points u, v in P it holds: (1 - e) ||u - v||2 ≤ ||f(u) – f(v)||2 ≤ (1 + e) ||u-v||2 Where k = O(e-2 log n) f() is called JL-embedding Setting v=0 we also get a bound on f(u)’s stretching!!!

What about the cosine-distance ? f(u)’s, f(v)’s stretching substituting formula above for ||u-v||2

How to compute a JL-embedding? If we set the projection matrix P = pi, j as a random m x k matrix, where its components are independent random variables with one of the following two distributions: E[ri, j] = 0 Var[ri, j] = 1

Finally. . . R Random projections hide large constants v k (1/e)2 * log n, so k may be large… v it is simple and fast to compute R LSI is intuitive and may scale to any k v optimal under various metrics v but costly to compute, do exist good libraries