P O D Solve by substitution to find

P. O. D- Solve by substitution to find the solution (x, y) Y = 2 x 2 x + y = -4

Learning Objective Students will find the solution of a system of linear equations algebraically by using substitution CCLS: 8 EE. 8 Analyze and solve pairs of simultaneous linear equations. 8 EE. 8. b Solve systems of two linear equations in two variables algebraically, and estimate solutions by graphing the equations. Solve simple cases by inspection.

What is Substitution? l Substitution is when you replace one thing with another thing. l Substitution is ideal to use if one of the variables has already been isolated in the original system of equations. Example: y = -2 x + 3

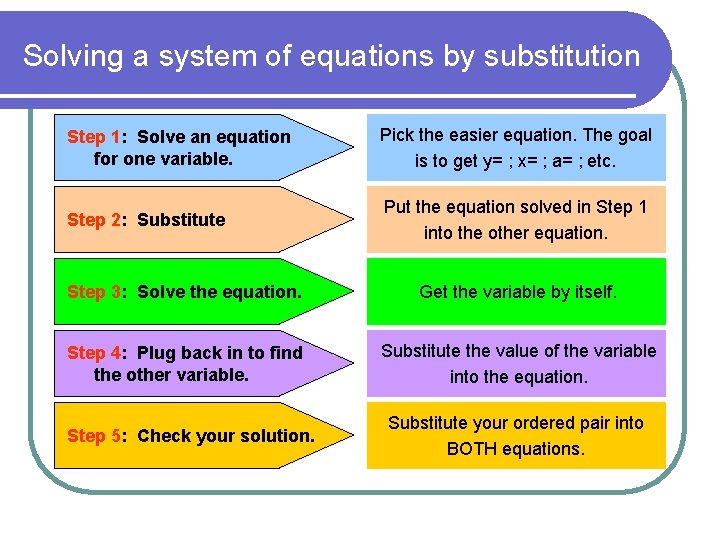
Solving a system of equations by substitution Step 1: Solve an equation for one variable. Pick the easier equation. The goal is to get y= ; x= ; a= ; etc. Step 2: Substitute Put the equation solved in Step 1 into the other equation. Step 3: Solve the equation. Get the variable by itself. Step 4: Plug back in to find the other variable. Substitute the value of the variable into the equation. Step 5: Check your solution. Substitute your ordered pair into BOTH equations.

Model Problem #1 Solve the following system of linear equations using substitution. x + y = 56 (1) y = 7 x + 8 (2) From (2) substitute y = 7 x + 8 into equation (1).

Model Problem# 1 (Continued) Substitute x = 6 into equation (1) x + y = 56 Check solution x = 6 and y = x + y = 56 (1) y = 7 x + 8 (2) in equation (2)

Model Problem #2 Solve the following system of linear equations using substitution. 3 x + 4 y = -4 (1) ¾ x + y = -1 (2) From (2) substitute y = into equation (1).

What does it mean if the result is “TRUE”? 1. 2. 3. 4. 5. The lines intersect The lines are parallel The lines are coinciding (The same) The lines reciprocate I can spell my name

Model Problem #3 Solve the following system of linear equations using substitution. 5 x – 4 y = 2 (1) 5 x - 4 y = 3 (2)

Ex. 3 x – y = 26 (1) 4 x + 5 y = 3 (2) Since no variables are isolated, we need to isolate one before we can substitute.

Ex. (Continued) Substitute into y = 3 x – 26 into (2). Substitute x = into (1).

Ex. (Continued) Check solution x = 7 and y = -5 into (2)

P. O. D. – On Slates Solve the following equation for y: 2 x – y = 8 Solve the following equation for x: 5 x + y = -25

Learning Objective Students will find the solution of a system of linear equations algebraically by using substitution CCLS: 8 EE. 8 Analyze and solve pairs of simultaneous linear equations. 8 EE. 8. b Solve systems of two linear equations in two variables algebraically, and estimate solutions by graphing the equations. Solve simple cases by inspection.

Ex. Solve the system of equations using substitution: -5 x + y = -3 3 x – 8 y = 24

White Board Drill – Solve by substitution x+y=5 y=3+x More Practice 1) 2 x + 4 y = 4 3 x + 2 y = 22 2) x = 3 – y x+y=7 3) 2 x + y = 4 4 x + 2 y = 8

Reflection Given the system of equations 2 x + y = 20 and 6 x – 5 y = 12 Solve and Justify in words how you would solve finding (x, y).