P 1 Graphs and Models Im so to
















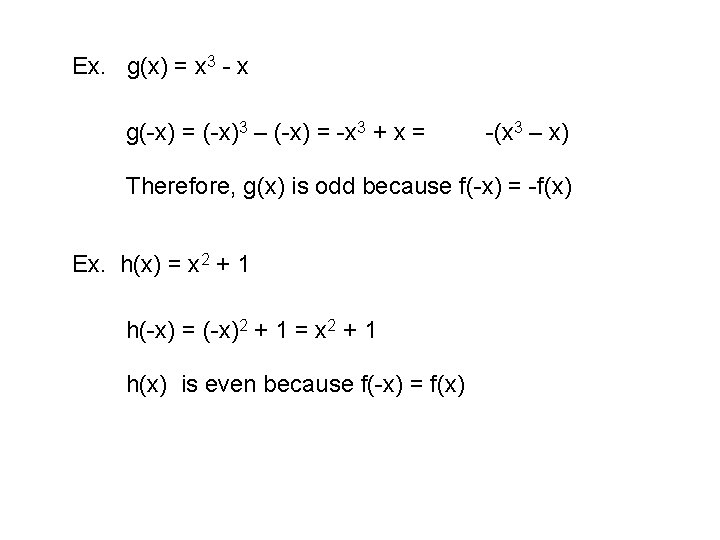



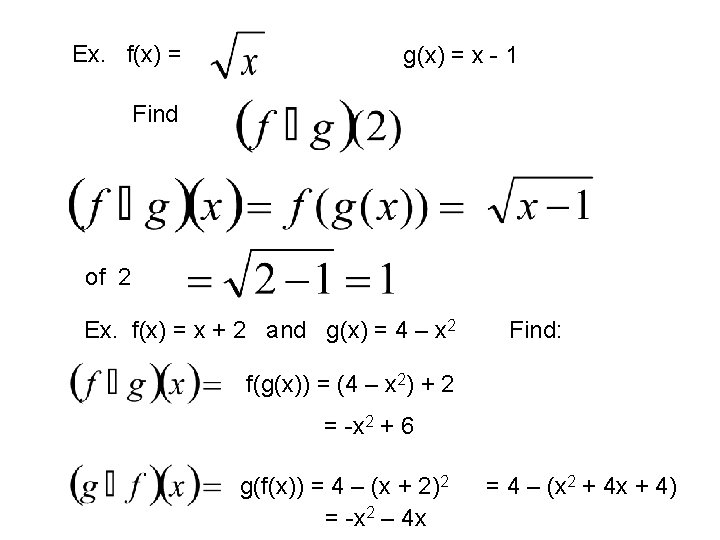

- Slides: 28

P. 1 Graphs and Models I’m so to be in Calculus!!!

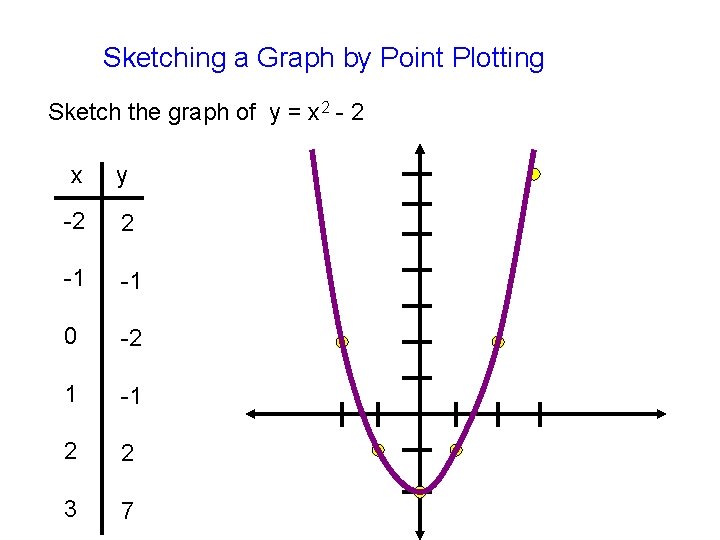
Sketching a Graph by Point Plotting Sketch the graph of y = x 2 - 2 x y -2 2 -1 -1 0 -2 1 -1 2 2 3 7

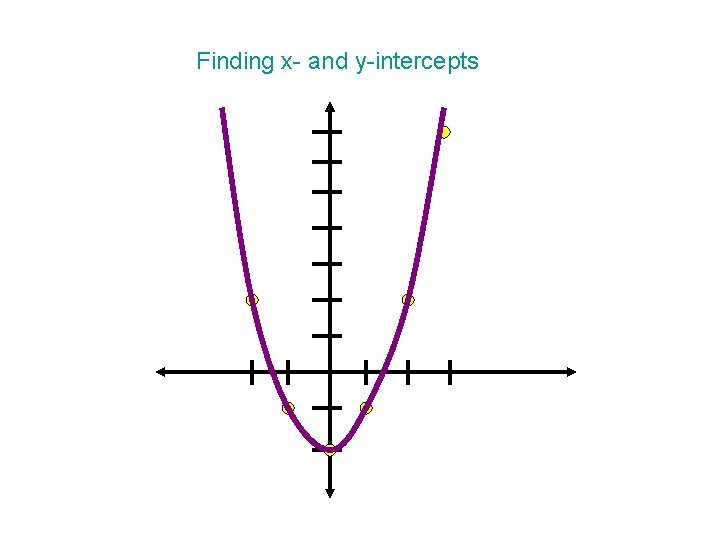
Finding x- and y-intercepts

Find the x- and y-intercepts of the graph of y = x 3 - 4 x To find the x-intercepts, let y be zero and solve for x. 0 = x 3 - 4 x This factors into? x(x - 2)(x + 2) = 0 the graph has the three x = 0, 2, or -2 x-intercepts: (0, 0), (2, 0), (-2, 0) To find the y-intercepts, let x = 0. y = 03 - 4(0) This produces y = 0. So, the y-intercept is (0, 0).

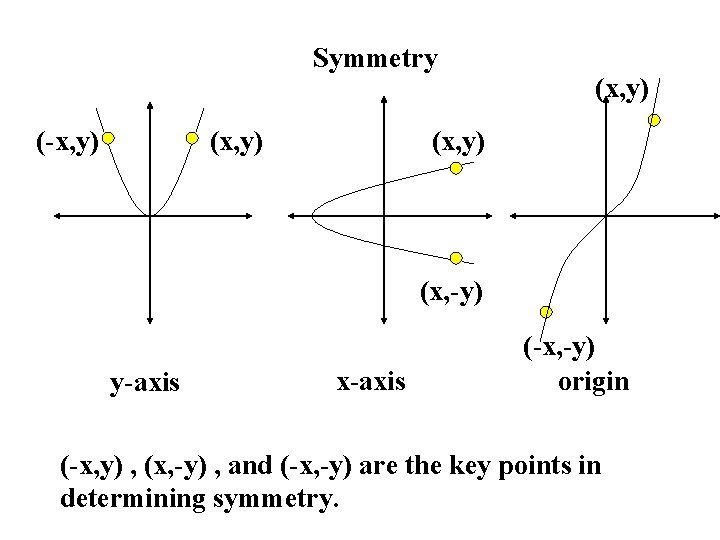
Symmetry (-x, y) (x, -y) y-axis x-axis (-x, -y) origin (-x, y) , (x, -y) , and (-x, -y) are the key points in determining symmetry.

Check for symmetry with respect to both axes and the origin. Ex. 4 xy 3 + 10 = 0 Plug in the three ordered pairs. If you can get it to look like the original equation, it has that symmetry. y-axis (-x, y) x-axis (x, -y) origin (-x, -y) (-x)y 3 + 10 = 0 Is this, or can we get this to look like -xy 3 + 10 = 0 the original? No. x(-y)3 + 10 = 0 -xy 3 + 10 = 0 Not like the original. (-x)(-y)3 + 10 = 0 This graph has origin symmetry. xy 3 + 10 = 0

P. 2 Linear Models and Rates of Change Calculus is a Celebration!!!

Slope of a Line Find the slope of the lines passing through… a. (-2, 0) and (3, 1) b. (-1, 2) and (2, 2) c. (4, -3) and (4, 5)

Point-slope Form of the Equation of a Line Given a point (x 1, y 1) and slope m y – y 1 = m(x – x 1) Ex. Find an equation of the line that passes through the point (1, -2) and has a slope of 3. y – (-2) = 3(x – 1) y + 2 = 3(x – 1) 0 = 3 x – y - 5

Summary of Equations of Lines 1. 2. 3. 4. 5. General Form Vertical Line Horizontal Liney = b Slope-intercept Point-slope form Ax + By + C = 0 x=a y = mx + b y – y 1 = m(x – x 1) Parallel lines have slopes that are Equal. Perpendicular lines have negative reciprocal slopes.

Ex. Find the equations of the lines that pass through the point (2, -1) and are a. ) parallel to and b. ) perpendicular to the line 2 x – 3 y = 5. First, solve for y and find the slope of the line. a. ) m = 2/3 Use point-slope form Mult. each term by 3. 3 y + 3 = 2 x - 4 0 = 2 x – 3 y – 7 or

b. ) What is our slope? Use point-slope form to start. Then put in general form. Dist. Mult. By 2

Calculus is something to P. 3 Functions and Their Graphs about!!!

Functions Function - for every x there is exactly one y. Domain - set of x-values Range - set of y-values

Tell whether the equations represent y as a function of x. a. x 2 + y = 1 Solve for y. y = 1 – x 2 For every number we plug in for x, do we get more than one y out? No, so this equation is a function. b. -x + y 2 = 1 Solve for y. y 2 = x + 1 Here we have 2 y’s for each x that we plug in. Therefore, this equation is not a function.

Find the domain of each function. a. f: {(-3, 0), (-1, 4), (0, 2), (2, 2), (4, -1)} Domain = { -3, -1, 0, 2, 4} b. D: Set 4 – x 2 greater than or = to 0, then factor, find C. N. ’s and test each interval. c. D: [-2, 2]

Ex. g(x) = -x 2 + 4 x + 1 Find: a. g(2) b. g(t) c. g(x+2) d. g(x + h) Ex. Evaluate at x = -1, 0, 1 Ans. 2, -1, 0

Ex. f(x) = x 2 – 4 x + 7 Find. = 2 x + h - 4

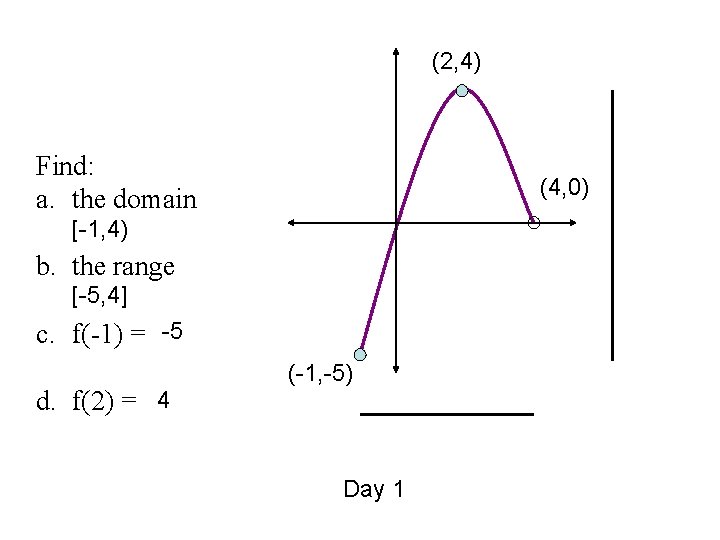
(2, 4) Find: a. the domain (4, 0) [-1, 4) b. the range [-5, 4] c. f(-1) = -5 d. f(2) = 4 (-1, -5) Day 1

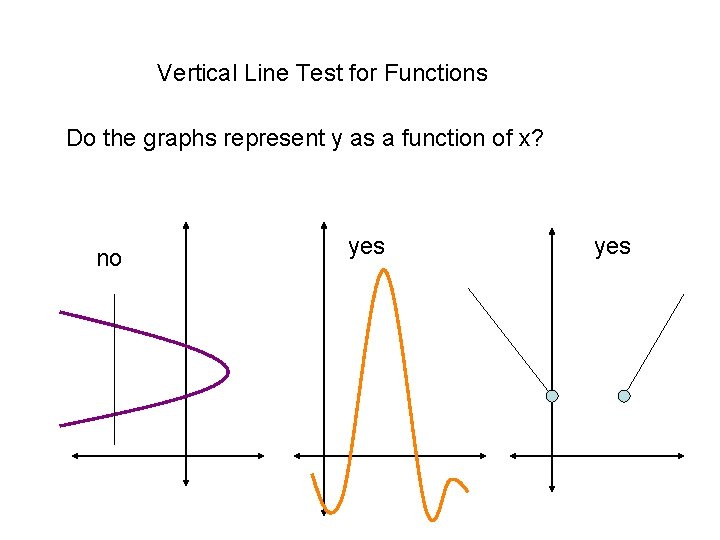
Vertical Line Test for Functions Do the graphs represent y as a function of x? no yes

Tests for Even and Odd Functions A function is y = f(x) is even if, for each x in the domain of f, f(-x) = f(x) An even function is symmetric about the y-axis. A function is y = f(x) is odd if, for each x in the domain of f, f(-x) = -f(x) An odd function is symmetric about the origin.
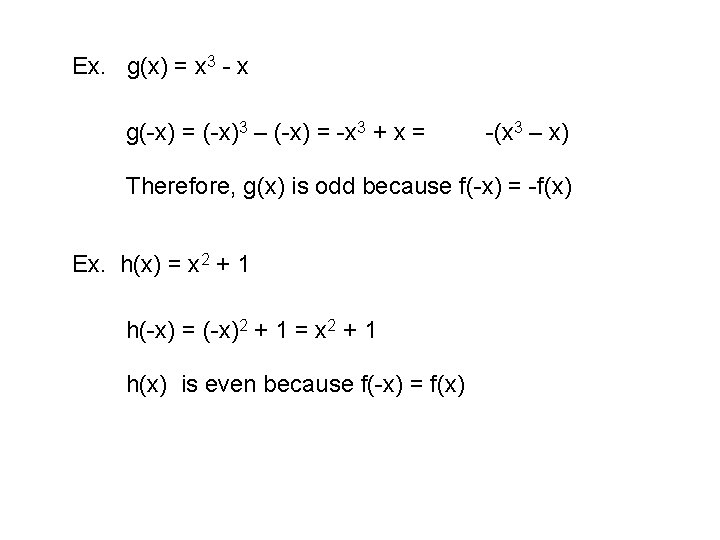
Ex. g(x) = x 3 - x g(-x) = (-x)3 – (-x) = -x 3 + x = -(x 3 – x) Therefore, g(x) is odd because f(-x) = -f(x) Ex. h(x) = x 2 + 1 h(-x) = (-x)2 + 1 = x 2 + 1 h(x) is even because f(-x) = f(x)

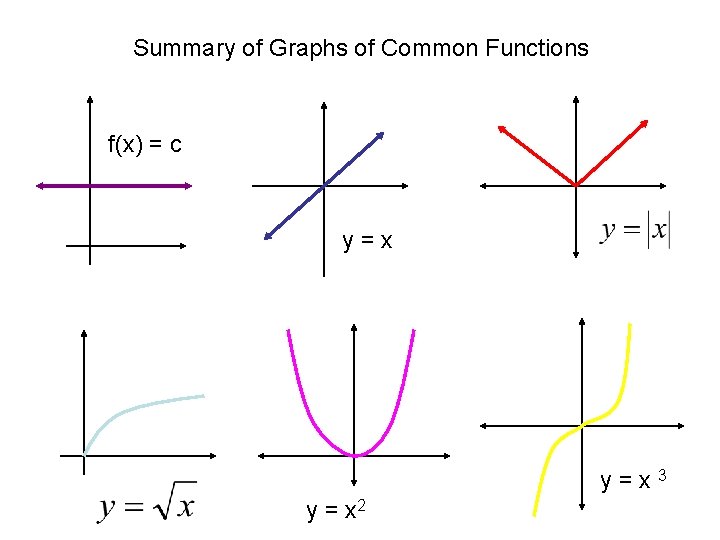
Summary of Graphs of Common Functions f(x) = c y=x 3 y = x 2

Vertical and Horizontal Shifts On calculator, graph y = x 2 + 2 y = x 2 - 3 y = (x – 1)2 y = (x + 2)2 y = -x 2 y = -(x + 3)2 -1

Vertical and Horizontal Shifts 1. h(x) = f(x) + c Vert. shift up 2. h(x) = f(x) - c Vert. shift down 3. h(x) = f(x – c) Horiz. shift right 4. h(x) = f(x + c) Horiz. shift left 5. h(x) = -f(x) Reflection in the x-axis 6. h(x) = f(-x) Reflection in the y-axis

Combinations of Functions The composition of the functions f and g is “f composed by g of x equals f of g of x”
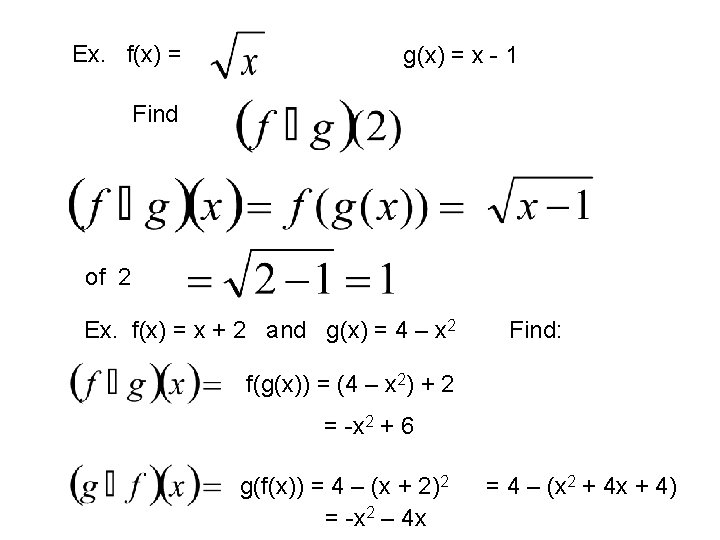
Ex. f(x) = g(x) = x - 1 Find of 2 Ex. f(x) = x + 2 and g(x) = 4 – x 2 Find: f(g(x)) = (4 – x 2) + 2 = -x 2 + 6 g(f(x)) = 4 – (x + 2)2 = -x 2 – 4 x = 4 – (x 2 + 4 x + 4)

Ex. Express h(x) = of two functions f and g. f(x) = g(x) = x-2 as a composition