p 01 Rate Eqn Order of Rxn C

p. 01 Rate Eqn. & Order of Rxn C. Y. Yeung (CHW, 2009)

p. 02 Rate Equation (Rate Law) the mathematical equation relating the rate of rxn to the [reactants]. Examples: 3 A + 2 B C rate x y [A] [B] order of rxn w. r. t. [A] order of rxn w. r. t. [B]

p. 03 rate x y = k[A] [B] rate constant (varies with temp. !!) * usually, order of reaction = 0, 1 or 2. Therefore, the rate equation shows that: rate of rxn is affected by [reactants] rate of rxn is affected by temperature

p. 04 Example: rate = k [A]m[B]n If [B] and temp. are kept constant, when [A] doubles, rate of reaction increases 4 times. Find the value of m. rate = k’ [A]m rate 1 = k’ [A]m and rate 2 = k’ (2[A])m 1 rate 1 k’ [A]m then = = m rate 2 k’ (2[A]) 4 1 m 1 = 2 4 the rxn is 2 nd order w. r. t. [A]. m=2

p. 05 If [B] and temp. are kept constant, when [A] doubles, rate of reaction increases 4 times. How to do it? [A] Expt. 1 [A]01 03 [B] Initial rate [A] 02 [B] Rate 1 [A]01 Expt. 2 [A]02 [B] Rate 2 Expt. 3 [A]03 [B] Rate 3 …. . [A] …. . t initial rate method kept constant Repeat expt. with constant [A] and different [B], find n!

Determination of k, m and n by graphical rate = k’ [A]m [A] [B] Initial rate Expt. 1 [A]1 [B] Rate 1 Expt. 2 [A]2 [B] Rate 2 Expt. 3 [A]3 [B] Rate 3 …. . p. 06 method Plot rate vs [A] : rate m=1 m=2 m=0 …. . [A] Only m could be found!

p. 07 rate = k’ [A]m log (rate) = m log [A] + log k’ y = mx + c log (rate) m=2 m=1 log k’ m=0 log [A] i. e. Both k (=k’/[B]) and m could be found!

1992 Paper II, Q. 2(a) p. 08

1992 Paper II, Q. 2(a) : Ans. p. 09

Differential Rate Equation: rate = - d[A] dt if m = 0 - d[A] dt = p. 10 slope of tangent at a point on the conc. - time graph. (NOT accurate!) m k’ [A] when t = 0, [A] = [A]0 = k’ - d[A] = k’dt - d[A] = k’ dt - [A] = k’t + C C = - [A]0 [A] = - k’t + [A]0 integrated rate eqn. (zeroth order) No calculation of tangent slope!

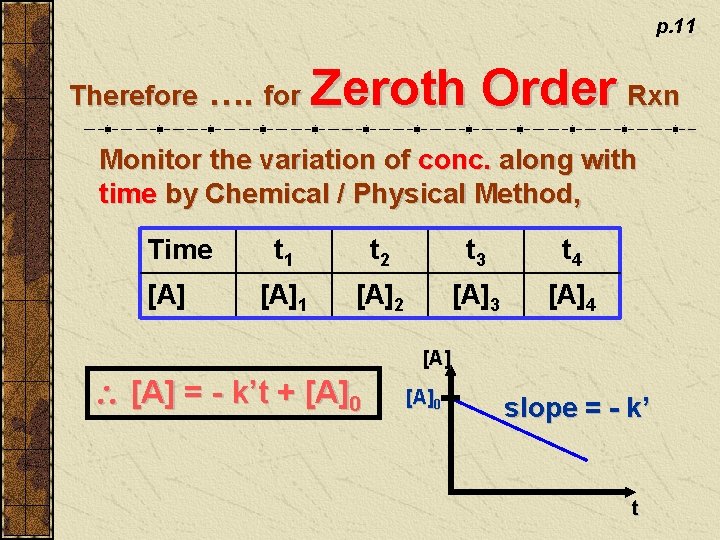
p. 11 Therefore …. for Zeroth Order Rxn Monitor the variation of conc. along with time by Chemical / Physical Method, Time [A] t 1 t 2 t 3 t 4 [A]1 [A]2 [A]3 [A]4 [A] = - k’t + [A]0 slope = - k’ t

p. 12 To conclude …. (1) Rate Equation shows that the rate of rxn is affected by conc. (order) & temp (k). Find the order of rxn (m, n) by Initial Rate Method (many combinations of [A] & [B]!) Plot log (rate) = m log[A] + log k’, both m, k’ and k could be found.

p. 13 To conclude …. (2) Initial Rate Method gives Differential Rate Equation, but m and k may not be accurately found from the initial rates (=slope of tangent). Integrated Rate Equation can give better m and k, as no calculation of tangent is involved.

p. 14 To conclude …. (3) To collect data for Integrated Rate Eqn. , only one combination of [A] & [B] is needed. Measure [A] at different t. Integrated Rate Eqn. of Zeroth Order: [A] = -k’t + [A]0

p. 15 Next …. Integrated Rate Eqn. of 1 st and 2 nd Order To study whether the decomposition of H 2 O 2 is 1 st order w. r. t. [H 2 O 2]. (expt. 8)

p. 16 Assignment Pre-lab [due date: 12/2(Thur)] p. 47 Q. 1 -6 [due date: 12/2(Thur)]