Oxide crystal structures The basics Ram Seshadri Materials

Oxide crystal structures: The basics Ram Seshadri Materials Department and Department of Chemistry & Biochemistry Materials Research Laboratory, University of California, Santa Barbara CA 93106 USA seshadri@mrl. ucsb. edu Materials 286 G, Spring 2020

en. wikipedia. org: Helen Dick Megaw (1 June 1907 – 26 February 2002) was an Irish crystallographer who was a pioneer in X-ray crystallography. She made measurements of the cell dimensions of ice and established the Perovskite crystal structure.

This lecture Brief description of oxide crystal structures 1. Ionic radii and Pauling’s rules 2. Electrostatic valence 3. Bond valence, and bond valence sums Connectivity and bandwidth 1. 2. 3. 4. 5. First rule: the radius ratio rule Second rule: the electrostatic valence rule Third rule: sharing of polyhedron corners, edges and faces Fourth rule: crystals containing different cations Fifth rule: the rule of parsimony

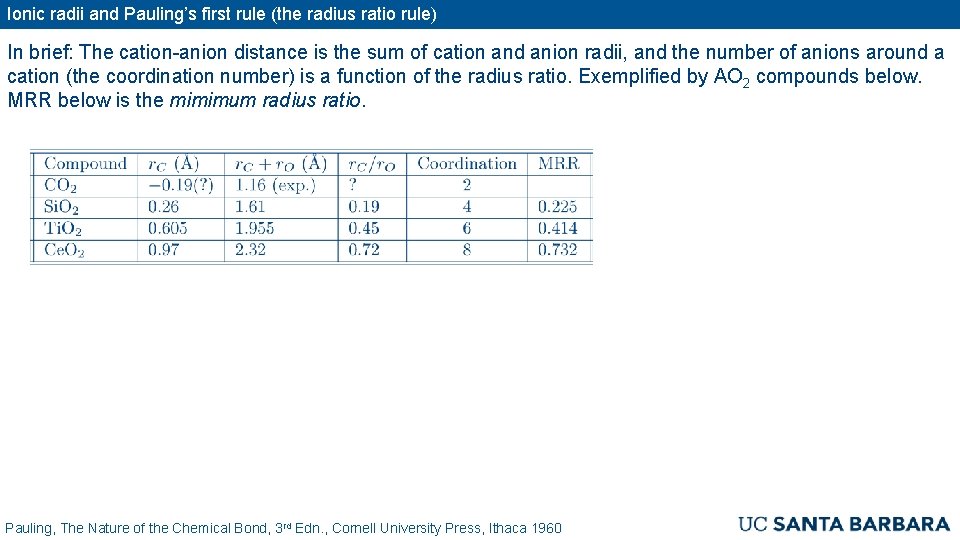
Ionic radii and Pauling’s first rule (the radius ratio rule) In brief: The cation-anion distance is the sum of cation and anion radii, and the number of anions around a cation (the coordination number) is a function of the radius ratio. Exemplified by AO 2 compounds below. MRR below is the mimimum radius ratio. Pauling, The Nature of the Chemical Bond, 3 rd Edn. , Cornell University Press, Ithaca 1960

Crystal structures of simple oxides [containing a single cation site]

Crystal structures of simple oxides [containing a single cation site] N. B. : Co. O is simple, Co 3 O 4 is not. Zn. Co 2 O 4 is certainly not ! Co 3 O 4 and Zn. Co 2 O 4 are complex oxides. Graphs of connectivity in crystals: Atoms are nodes and edges (the lines that connect nodes) indicate short (near-neighbor) distances. CO 2: The molecular structure is O=C=O. The graph is: Each C connected to 2 O, each O connected to a 1 C Os. O 4: The structure comprises isolated tetrahedra (molecular). The graph is below: Each Os connected to 4 O and each O to 1 Os

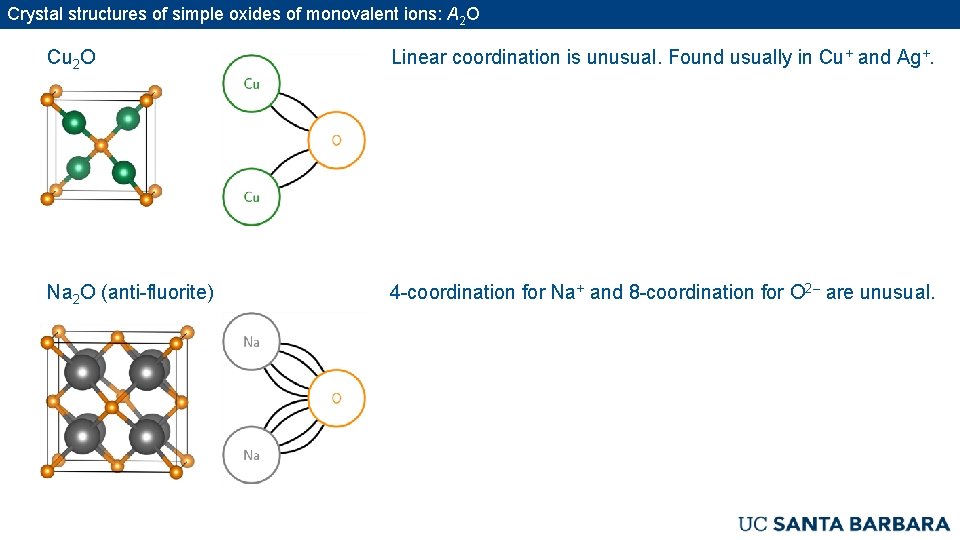
Crystal structures of simple oxides of monovalent ions: A 2 O Cu 2 O Linear coordination is unusual. Found usually in Cu+ and Ag+. Na 2 O (anti-fluorite) 4 -coordination for Na+ and 8 -coordination for O 2– are unusual.

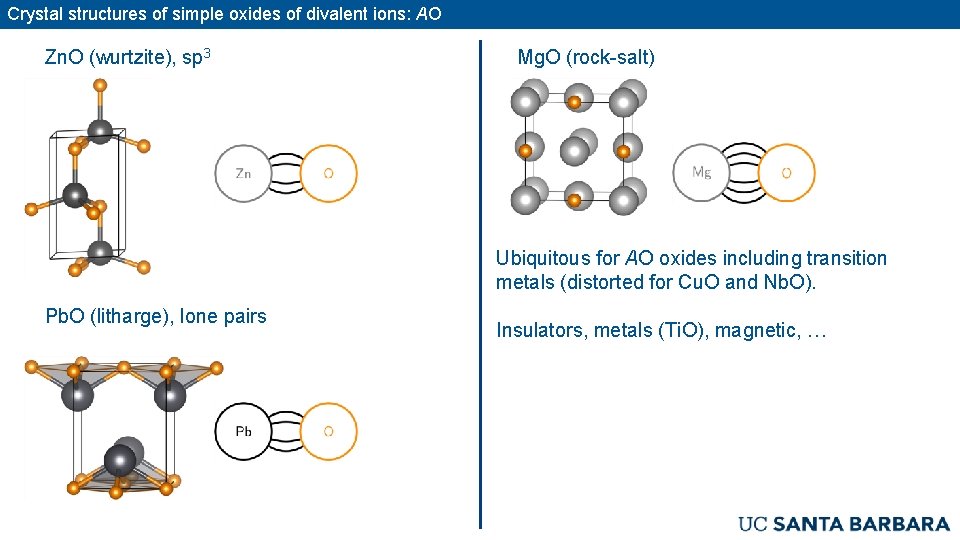
Crystal structures of simple oxides of divalent ions: AO Zn. O (wurtzite), sp 3 Mg. O (rock-salt) Ubiquitous for AO oxides including transition metals (distorted for Cu. O and Nb. O). Pb. O (litharge), lone pairs Insulators, metals (Ti. O), magnetic, …

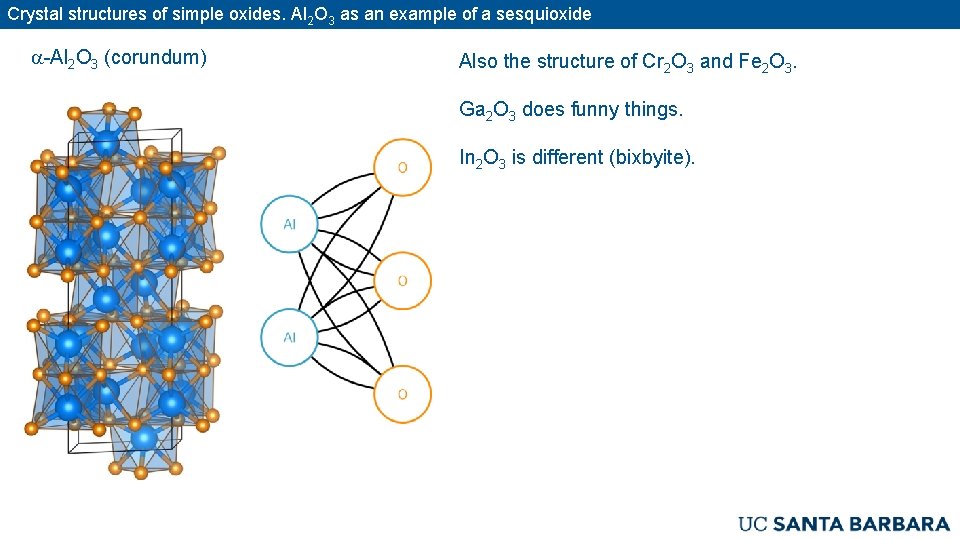
Crystal structures of simple oxides. Al 2 O 3 as an example of a sesquioxide a-Al 2 O 3 (corundum) Also the structure of Cr 2 O 3 and Fe 2 O 3. Ga 2 O 3 does funny things. In 2 O 3 is different (bixbyite).

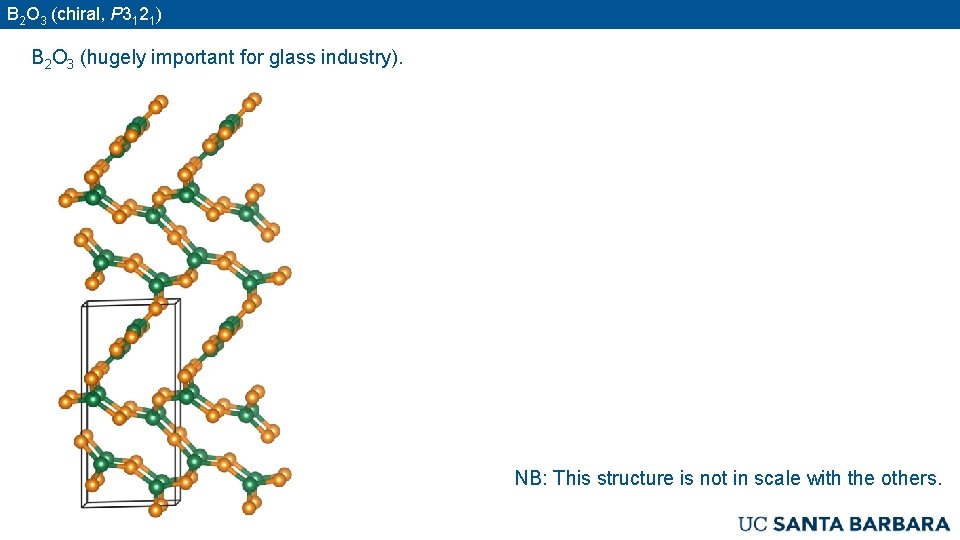
B 2 O 3 (chiral, P 3121) B 2 O 3 (hugely important for glass industry). NB: This structure is not in scale with the others.

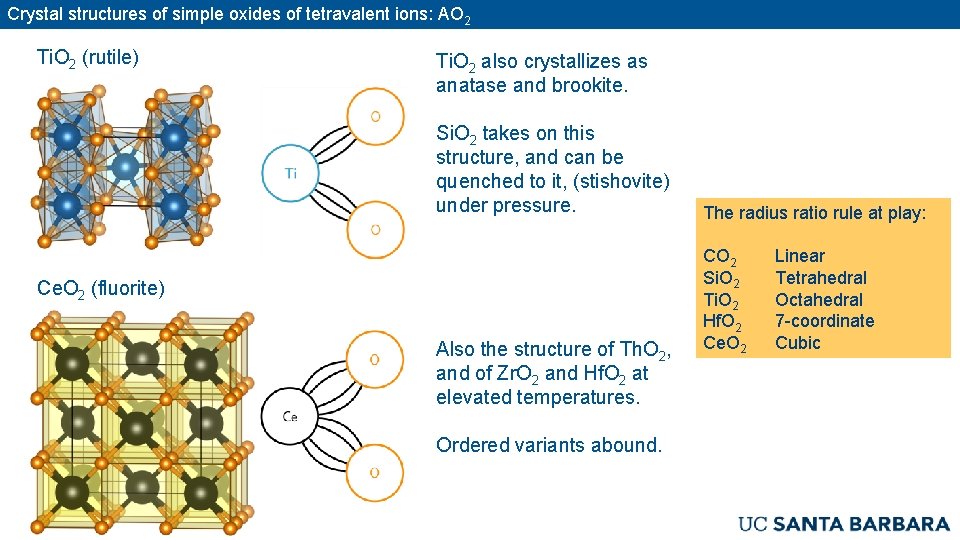
Crystal structures of simple oxides of tetravalent ions: AO 2 Ti. O 2 (rutile) Ti. O 2 also crystallizes as anatase and brookite. Si. O 2 takes on this structure, and can be quenched to it, (stishovite) under pressure. Ce. O 2 (fluorite) Also the structure of Th. O 2, and of Zr. O 2 and Hf. O 2 at elevated temperatures. Ordered variants abound. The radius ratio rule at play: CO 2 Si. O 2 Ti. O 2 Hf. O 2 Ce. O 2 Linear Tetrahedral Octahedral 7 -coordinate Cubic

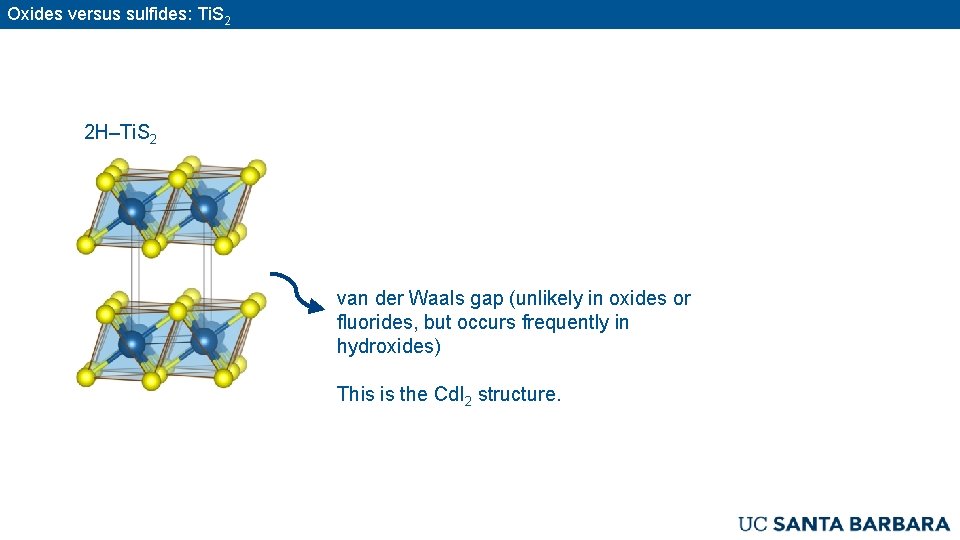
Oxides versus sulfides: Ti. S 2 2 H–Ti. S 2 van der Waals gap (unlikely in oxides or fluorides, but occurs frequently in hydroxides) This is the Cd. I 2 structure.

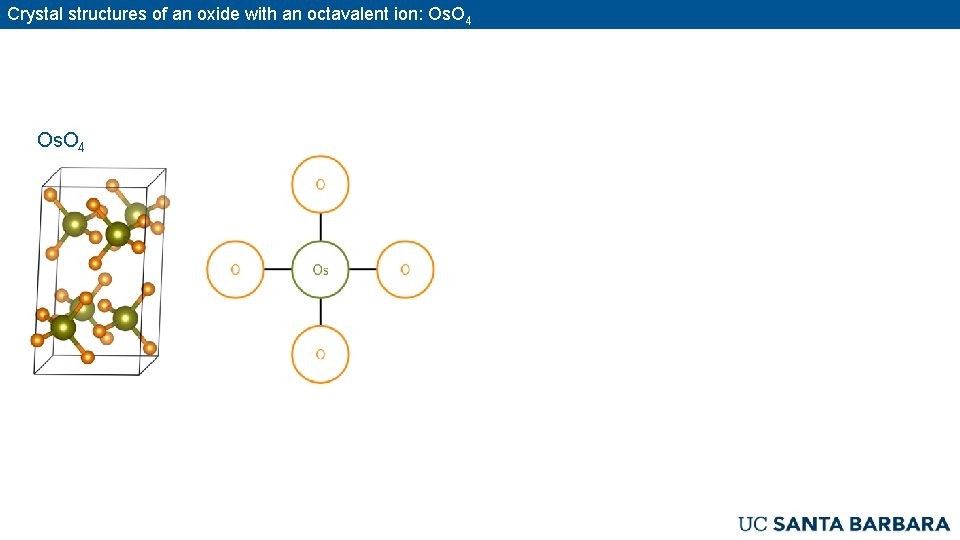
Crystal structures of an oxide with an octavalent ion: Os. O 4

Pauling’s second rule: The electrostatic valence rule In brief: Charges going out from cations should balance anions and vice-versa +1/2 +3/6 electrostatic bond strength or valence s = charge on cation/coordination number +8/4 Why is Os. O 4 a molecule? Radius ratio + electrostatic valence Pauling, The Nature of the Chemical Bond, 3 rd Edn. , Cornell University Press, Ithaca 1960

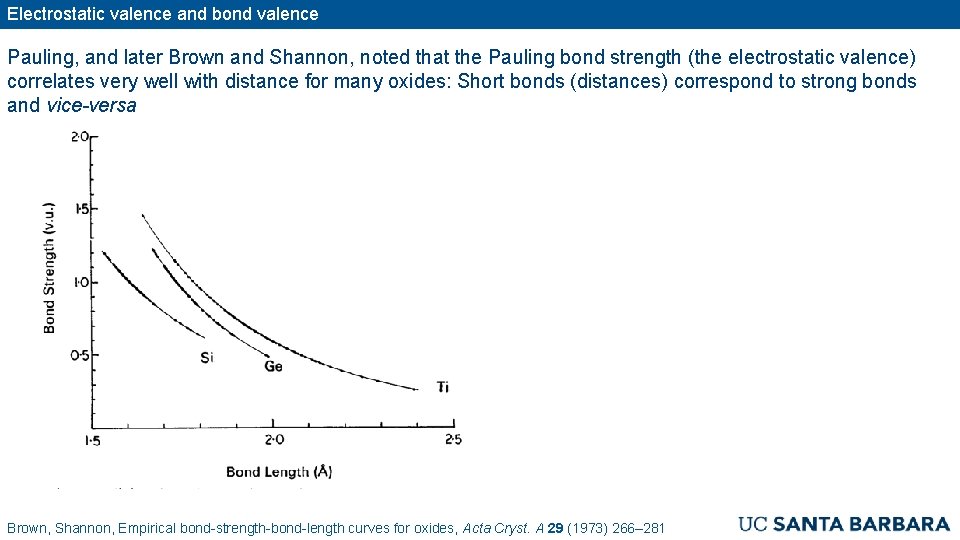
Electrostatic valence and bond valence Pauling, and later Brown and Shannon, noted that the Pauling bond strength (the electrostatic valence) correlates very well with distance for many oxides: Short bonds (distances) correspond to strong bonds and vice-versa Brown, Shannon, Empirical bond-strength-bond-length curves for oxides, Acta Cryst. A 29 (1973) 266– 281

Electrostatic valence and bond valence The modern bond valence relationship: Where s is the strength of the bond, R is the cation to anion distance, and R 0 and B ≈ 0. 37 Å are parametrized for the specific ion pair. When all s are calculated: s = +2/6 valence of the ion For Mn 2+–O 2–, R 0 = 1. 790 Å, B = 0. 37 Å. This means R = 2. 20 Å. experiment: 2. 22 Å Brown, Shannon, Empirical bond-strength-bond-length curves for oxides, Acta Cryst. A 29 (1973) 266– 281.

Electrostatic valence and bond valence: Parameters for Mn Mn Mn Mn Mn Mn Mn 2 2 2 2 2 3 3 3 4 4 4 6 7 7 O O S F Cl Br I N N O O F Cl N O O F F Cl N O O O F Cl -2 -2 -2 -1 -1 -1 -2 -3 -3 -2 -2 -1 -1 -1 -3 -2 -2 -2 -1 -1 1. 790 1. 765 2. 22 1. 698 2. 133 2. 34 2. 52 1. 849 1. 65 1. 760 1. 732 1. 66 2. 14 1. 837 1. 753 1. 750 1. 71 1. 63 2. 13 1. 822 1. 79 1. 827 1. 79 1. 72 2. 17 0. 37 0. 35 0. 37 0. 37 a j e a a e e j e a j b b j a j b e b j e e b bvsparm. cif

Crystal structures of some complex oxides [containing two or more cation sites]

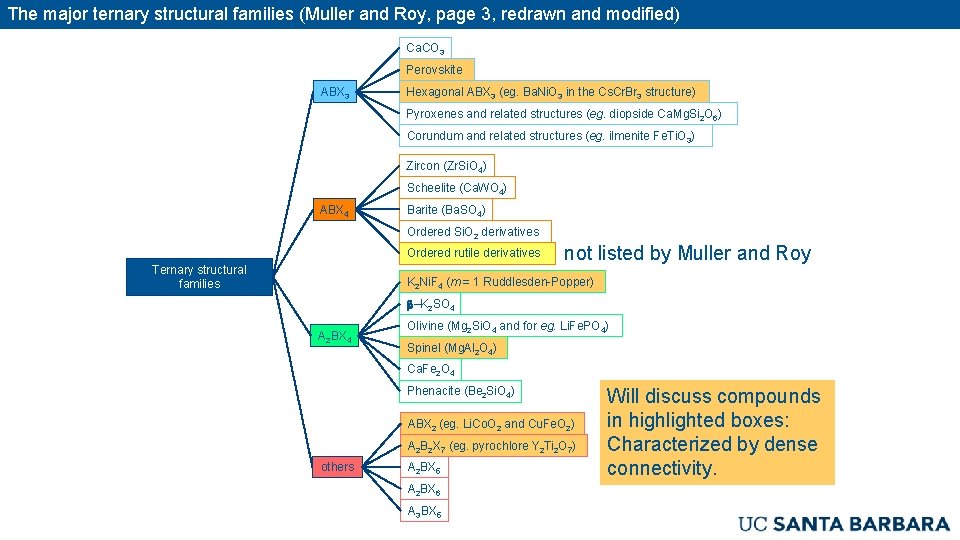
The major ternary structural families (Muller and Roy, page 3, redrawn and modified) Ca. CO 3 Perovskite ABX 3 Hexagonal ABX 3 (eg. Ba. Ni. O 3 in the Cs. Cr. Br 3 structure) Pyroxenes and related structures (eg. diopside Ca. Mg. Si 2 O 6) Corundum and related structures (eg. ilmenite Fe. Ti. O 3) Zircon (Zr. Si. O 4) Scheelite (Ca. WO 4) ABX 4 Barite (Ba. SO 4) Ordered Si. O 2 derivatives Ordered rutile derivatives Ternary structural families not listed by Muller and Roy K 2 Ni. F 4 (m = 1 Ruddlesden-Popper) b–K 2 SO 4 A 2 BX 4 Olivine (Mg 2 Si. O 4 and for eg. Li. Fe. PO 4) Spinel (Mg. Al 2 O 4) Ca. Fe 2 O 4 Phenacite (Be 2 Si. O 4) ABX 2 (eg. Li. Co. O 2 and Cu. Fe. O 2) A 2 B 2 X 7 (eg. pyrochlore Y 2 Ti 2 O 7) others A 2 BX 5 A 2 BX 6 A 3 BX 5 Will discuss compounds in highlighted boxes: Characterized by dense connectivity.

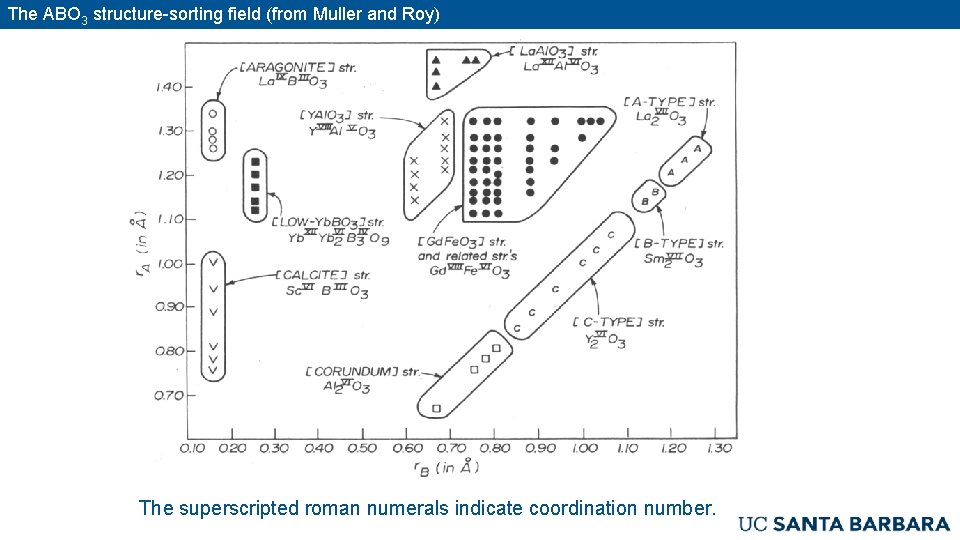
The ABO 3 structure-sorting field (from Muller and Roy) The superscripted roman numerals indicate coordination number.

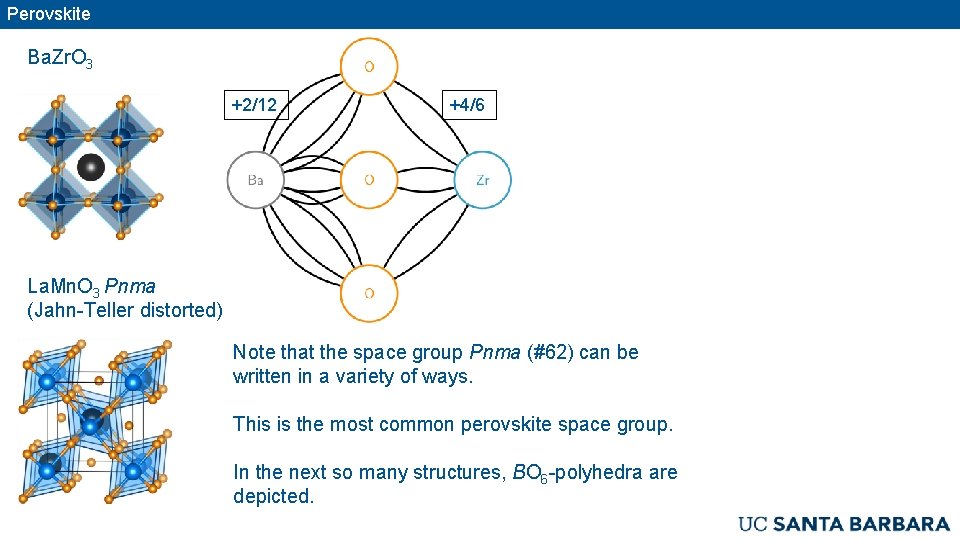
Perovskite Ba. Zr. O 3 +2/12 +4/6 La. Mn. O 3 Pnma (Jahn-Teller distorted) Note that the space group Pnma (#62) can be written in a variety of ways. This is the most common perovskite space group. In the next so many structures, BO 6 -polyhedra are depicted.

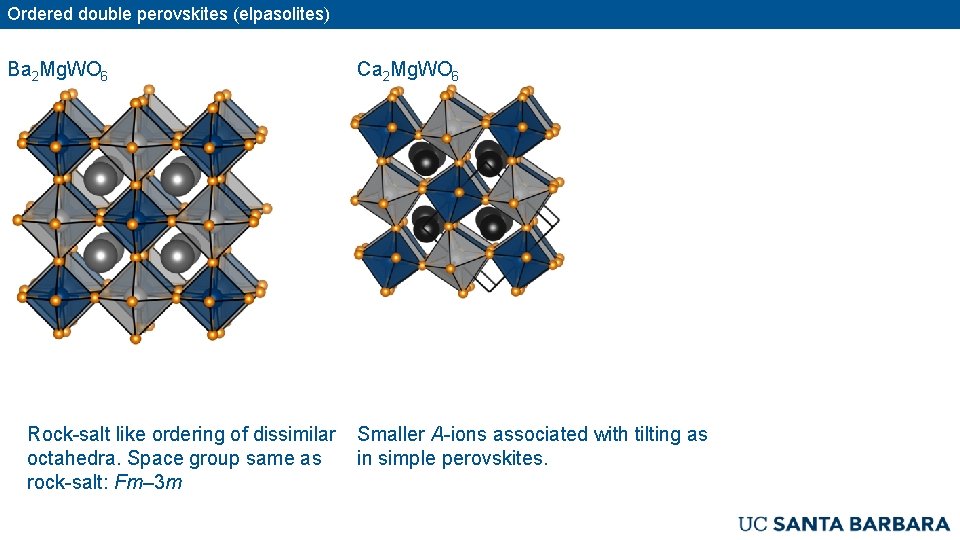
Ordered double perovskites (elpasolites) Ba 2 Mg. WO 6 Rock-salt like ordering of dissimilar octahedra. Space group same as rock-salt: Fm– 3 m Ca 2 Mg. WO 6 Smaller A-ions associated with tilting as in simple perovskites.

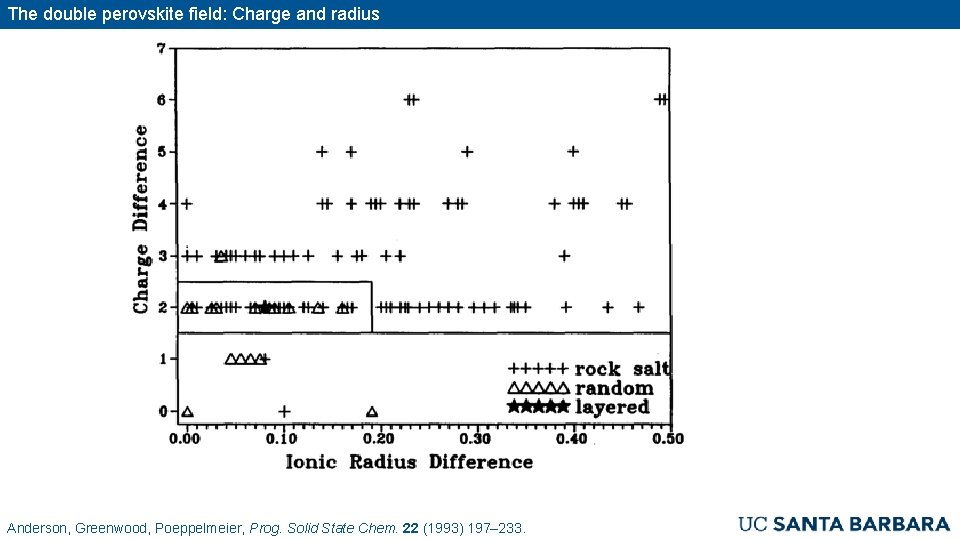
The double perovskite field: Charge and radius Anderson, Greenwood, Poeppelmeier, Prog. Solid State Chem. 22 (1993) 197– 233.

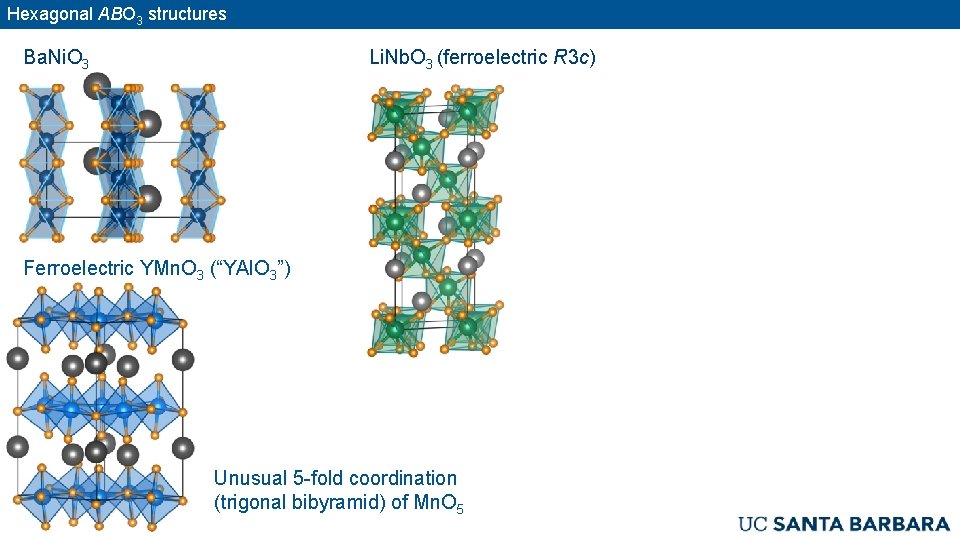
Hexagonal ABO 3 structures Ba. Ni. O 3 Li. Nb. O 3 (ferroelectric R 3 c) Ferroelectric YMn. O 3 (“YAl. O 3”) Unusual 5 -fold coordination (trigonal bibyramid) of Mn. O 5

Ordered rutiles (the trirutile), obtained through charge forking Co. Ta 2 O 6: 3×Ti. O 2 = Ti 3 O 6; 3×Ti 4+ = Co 2+ + 2×Ta 5+

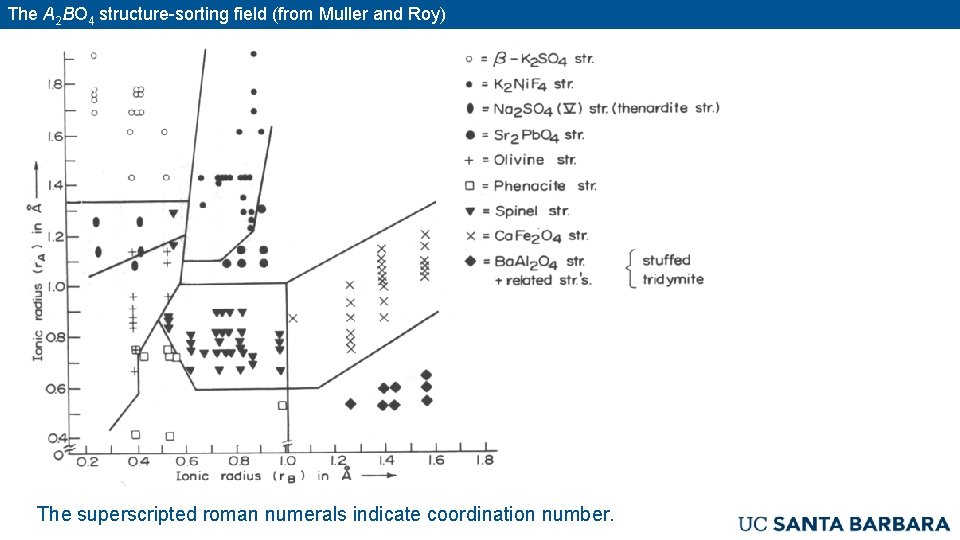
The A 2 BO 4 structure-sorting field (from Muller and Roy) The superscripted roman numerals indicate coordination number.

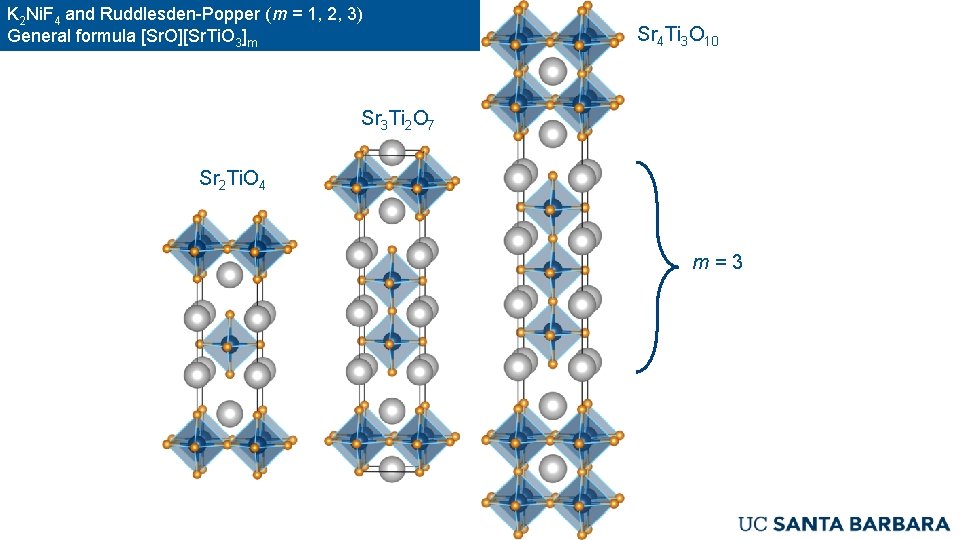
K 2 Ni. F 4 and Ruddlesden-Popper (m = 1, 2, 3) General formula [Sr. O][Sr. Ti. O 3]m Sr 4 Ti 3 O 10 Sr 3 Ti 2 O 7 Sr 2 Ti. O 4 m=3

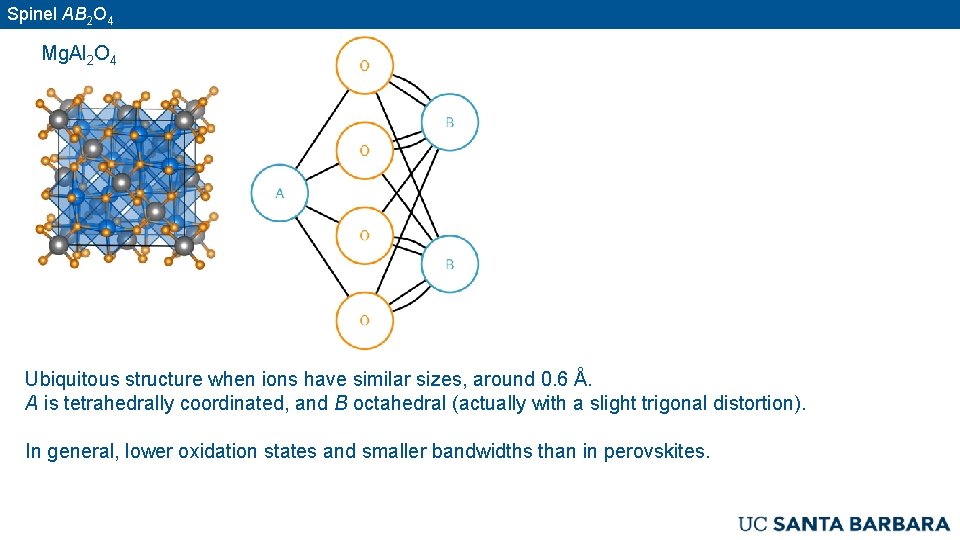
Spinel AB 2 O 4 Mg. Al 2 O 4 Ubiquitous structure when ions have similar sizes, around 0. 6 Å. A is tetrahedrally coordinated, and B octahedral (actually with a slight trigonal distortion). In general, lower oxidation states and smaller bandwidths than in perovskites.

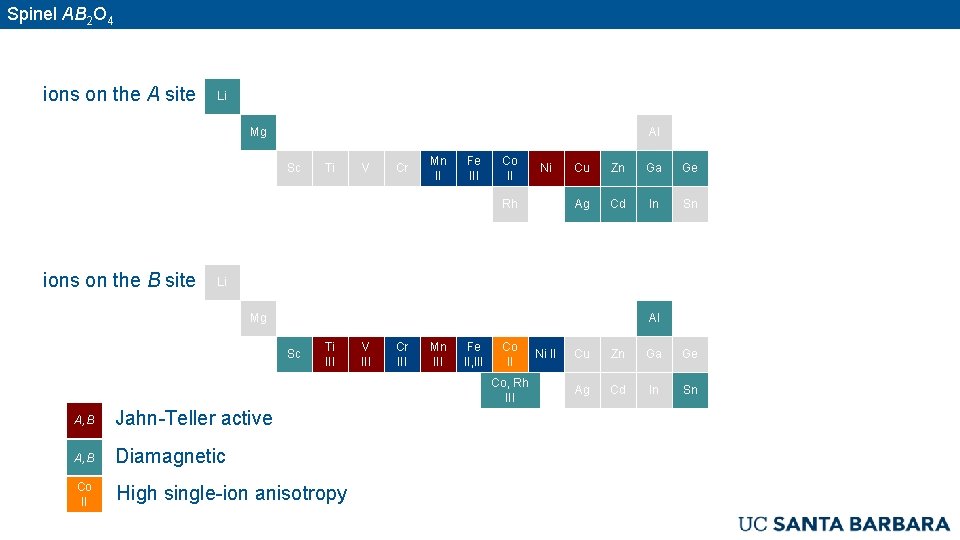
Spinel AB 2 O 4 ions on the A site Li Mg Al Sc Ti V Cr Mn II Fe III Co II Ni Rh ions on the B site Cu Zn Ga Ge Ag Cd In Sn Li Mg Al Sc Ti III V III Cr III Mn III Fe II, III Co, Rh III A, B Jahn-Teller active A, B Diamagnetic Co II High single-ion anisotropy Ni II Cu Zn Ga Ge Ag Cd In Sn

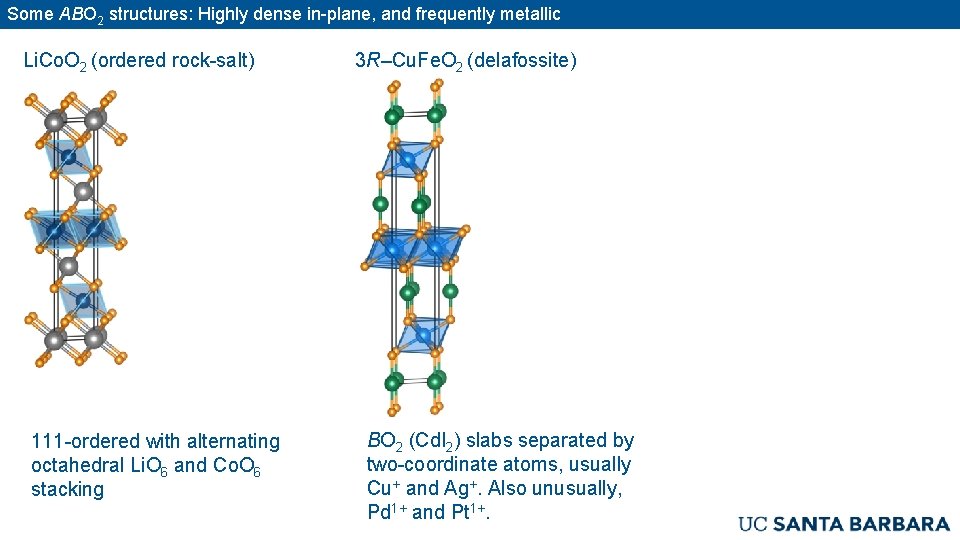
Some ABO 2 structures: Highly dense in-plane, and frequently metallic Li. Co. O 2 (ordered rock-salt) 111 -ordered with alternating octahedral Li. O 6 and Co. O 6 stacking 3 R–Cu. Fe. O 2 (delafossite) BO 2 (Cd. I 2) slabs separated by two-coordinate atoms, usually Cu+ and Ag+. Also unusually, Pd 1+ and Pt 1+.

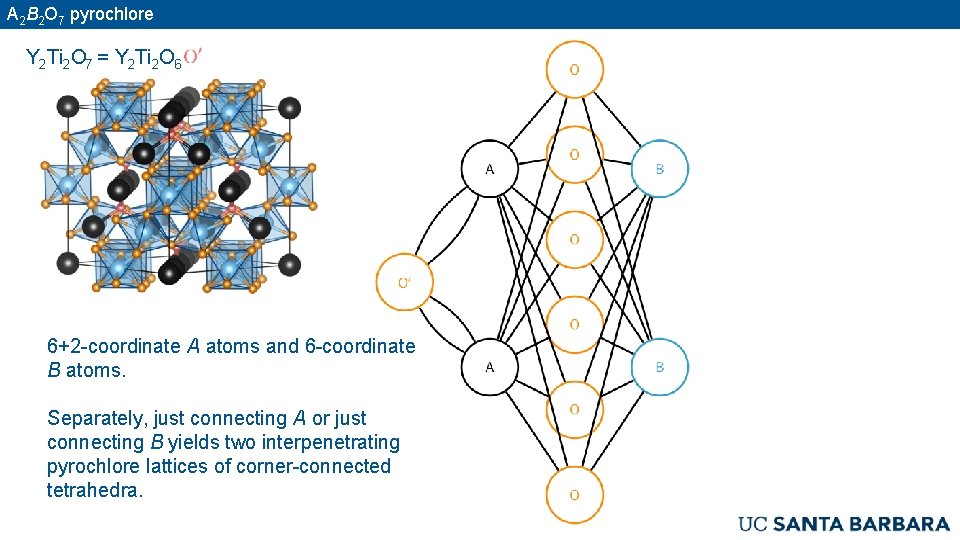
A 2 B 2 O 7 pyrochlore Y 2 Ti 2 O 7 = Y 2 Ti 2 O 6 6+2 -coordinate A atoms and 6 -coordinate B atoms. Separately, just connecting A or just connecting B yields two interpenetrating pyrochlore lattices of corner-connected tetrahedra.

Some examples of the structural principles covered

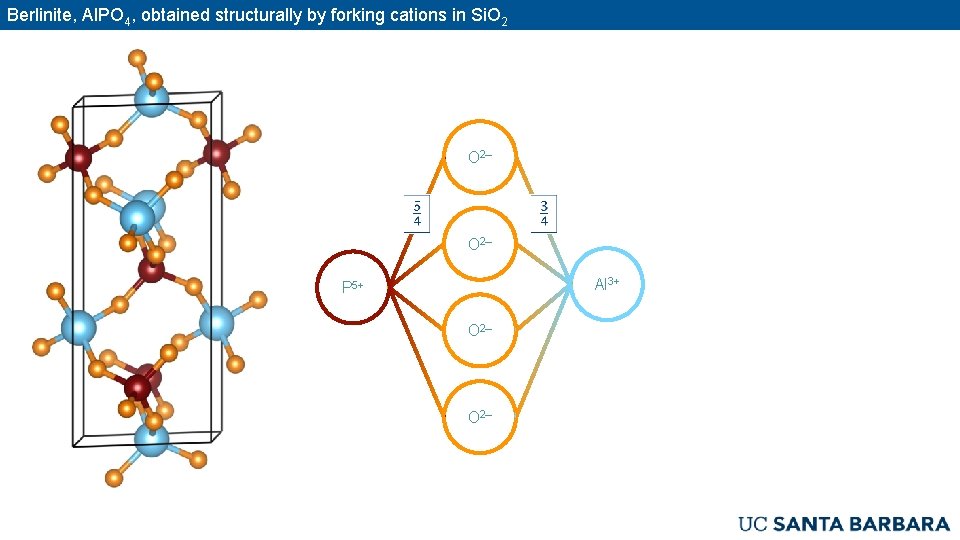
Berlinite, Al. PO 4, obtained structurally by forking cations in Si. O 2– Al 3+ P 5+ O 2–

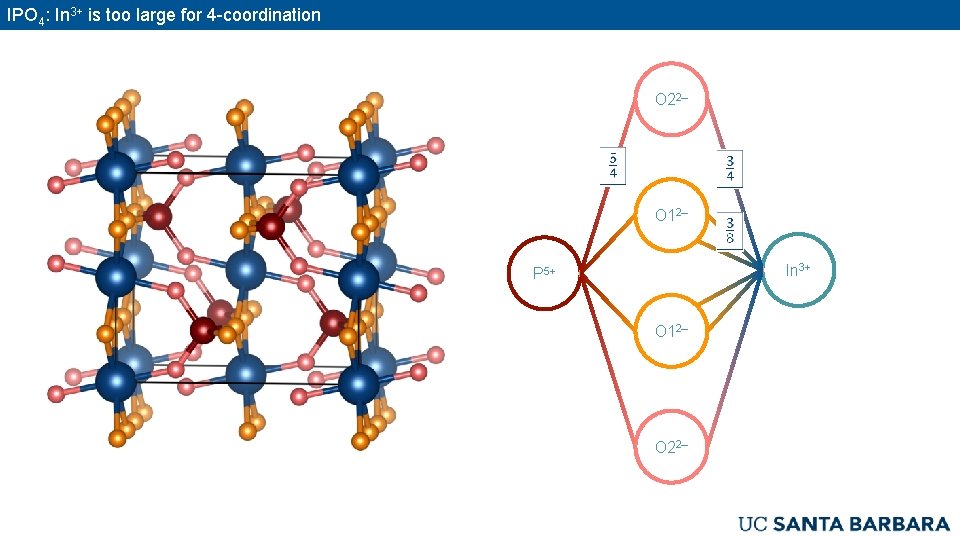
IPO 4: In 3+ is too large for 4 -coordination O 22– O 12– In 3+ P 5+ O 12– O 22–

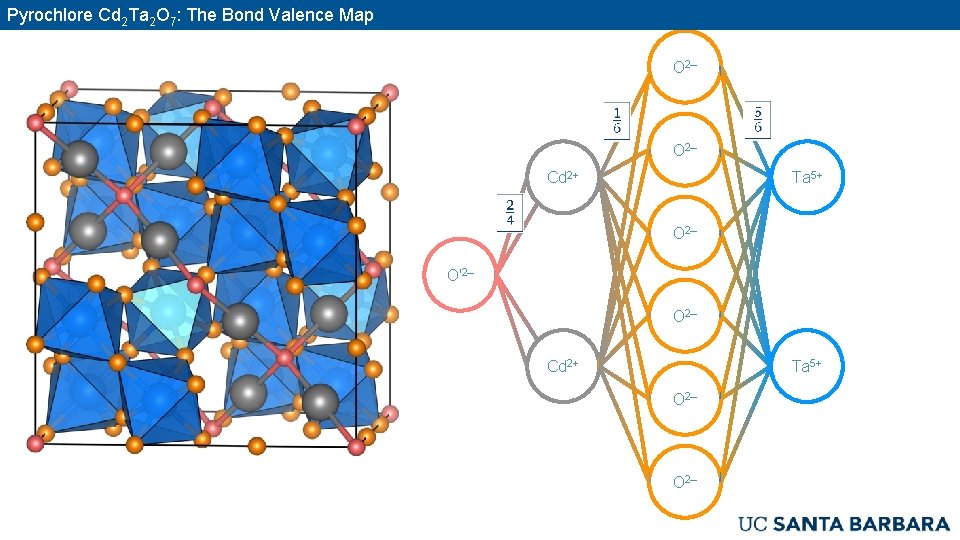
Pyrochlore Cd 2 Ta 2 O 7: The Bond Valence Map O 2– Cd 2+ Ta 5+ O 2– O′ 2– O 2– Cd 2+ Ta 5+ O 2–

End of these slides