Overview Pinhole model From 3 D to 2

Overview • Pin-hole model • From 3 D to 2 D • Camera projection • Homogeneous coordinates • Camera calibration • Vanishing points & lines • Perspective cues • Distortions

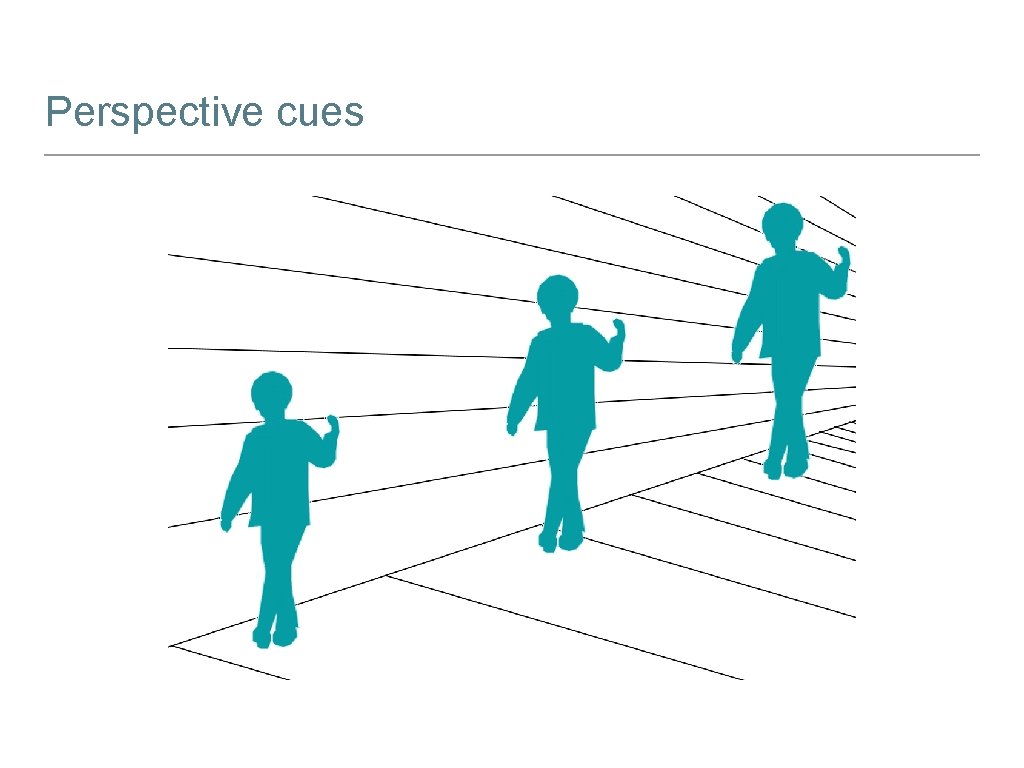
Perspective cues

Perspective cues

Perspective cues

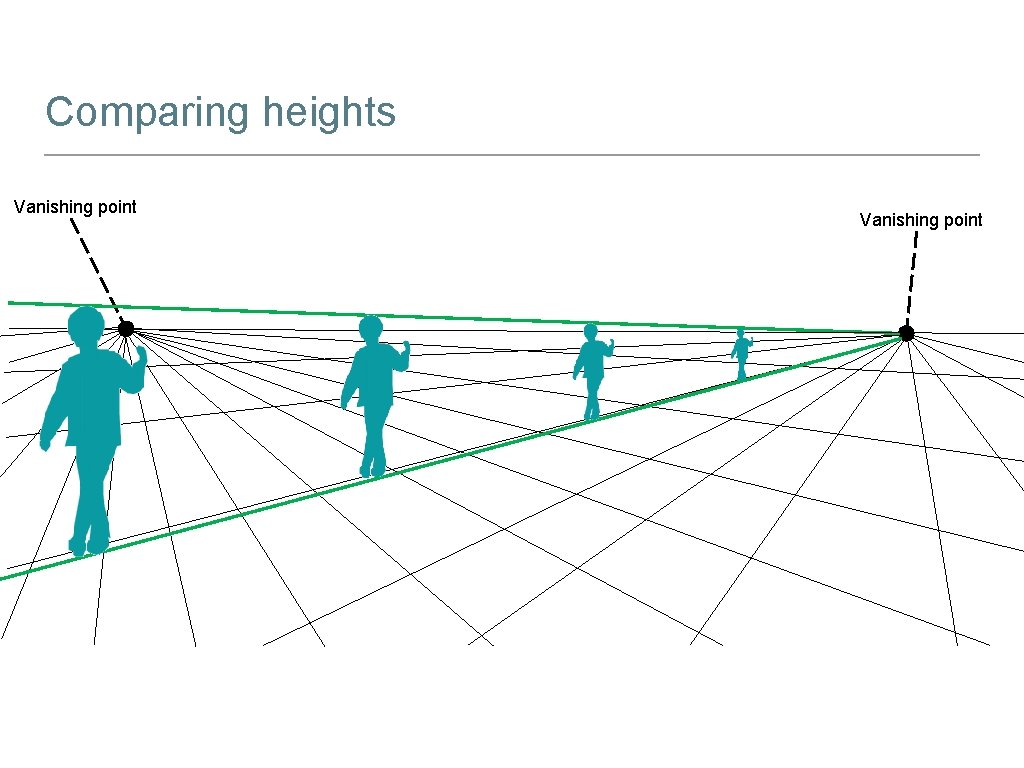
Comparing heights Vanishing point

Comparing heights Vanishing point

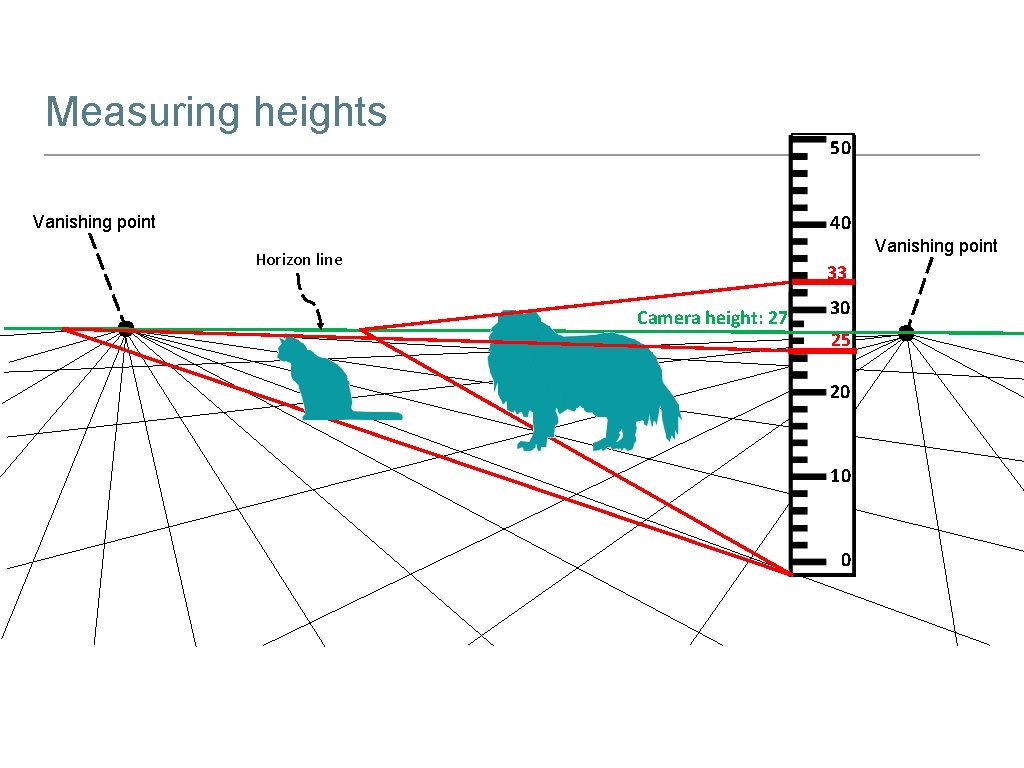
Measuring heights 50 40 Vanishing point Horizon line 33 Camera height: 27 30 25 20 10 0

The cross ratio • What if we have no ruler in the scene for the measuring? • Vanishing points are not enough for this task.

The cross ratio • The cross-ratio of 4 collinear points is the fundamental projection invariant of projective geometry. • The points ordering can be permuted. Therefore there are 4! = 24 different orders (but only 6 distinct values!)

The cross ratio

The cross ratio Scene cross ratio Image cross ratio

The cross ratio Vanishing point Horizon line Vanishing point

The cross ratio Vanishing point Horizon line Vanishing point

Overview • Pin-hole model • From 3 D to 2 D • Camera projection • Homogeneous coordinates • Camera calibration • Vanishing points & lines • Perspective cues • Distortions

Fronto-parallel planes • What happens to the projection of a pattern on a plane parallel to the image plane? • All points on that plane are at a fixed depth z • The pattern gets scaled by a factor of f/z, but angles and ratios of lengths/areas are preserved

Fronto-parallel planes • images from 1 X. com

Perspective distortions

Architectural photography

Architectural photography • When we want to take a photo of a tall building we may face a difficulty for capturing all the building in the wanted perspective. (a) Keeping the camera level, with an ordinary lens, captures only the bottom portion of the building.

Architectural photography • When we want to take a photo of a tall building we may face a difficulty for capturing all the building in the wanted perspective. (b) Tilting the camera upwards results in converging verticals.

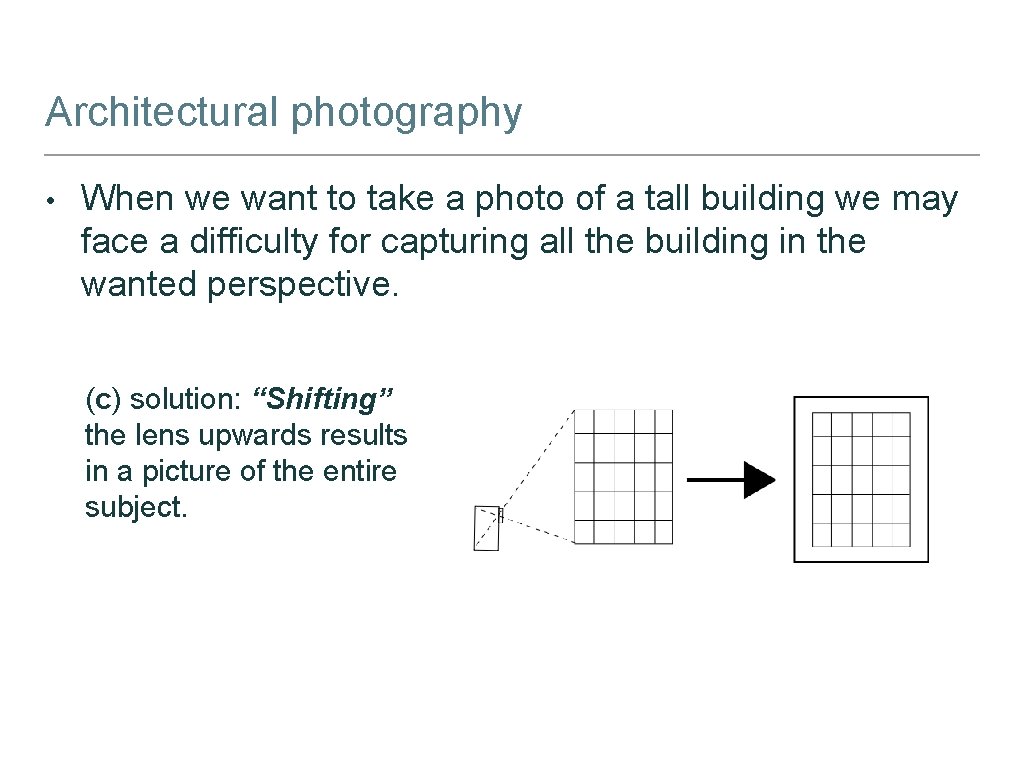
Architectural photography • When we want to take a photo of a tall building we may face a difficulty for capturing all the building in the wanted perspective. (c) solution: “Shifting” the lens upwards results in a picture of the entire subject.

Architectural photography • When we want to take a photo of a tall building we may face a difficulty for capturing all the building in the wanted perspective. (c) solution: “Shifting” the lens upwards results in a picture of the entire subject. • So how can we actually “shift” the lens of the camera for solving the problem?

Architectural photography • The solutions: • View camera – used by photographers for controlling focus and convergence of parallel lines. Image control is done by moving the front and/or rear standards.

Architectural photography • The solutions: • Tilt-Shift lens – a modern cameras solving this problem. Disadvantages: Tilting around the vertical axis resulted in a very small region in which objects appear sharp.

Tilt-Shift photography

Tilt-Shift photography

Tilt-Shift photography

Architectural photography • The solutions: • Homographic projections …

Points on the plane

Points on the plane • In many cases, such as the perspective distortions problem, we can consider some points in the image as on the same plane in the 3 D world. • Using an appropriate coordinates system for the scene, we can say all these points on the plane satisfy the fact that: Z = 0.

Points on the plane

Points on the plane

Points on the plane

Points on the plane

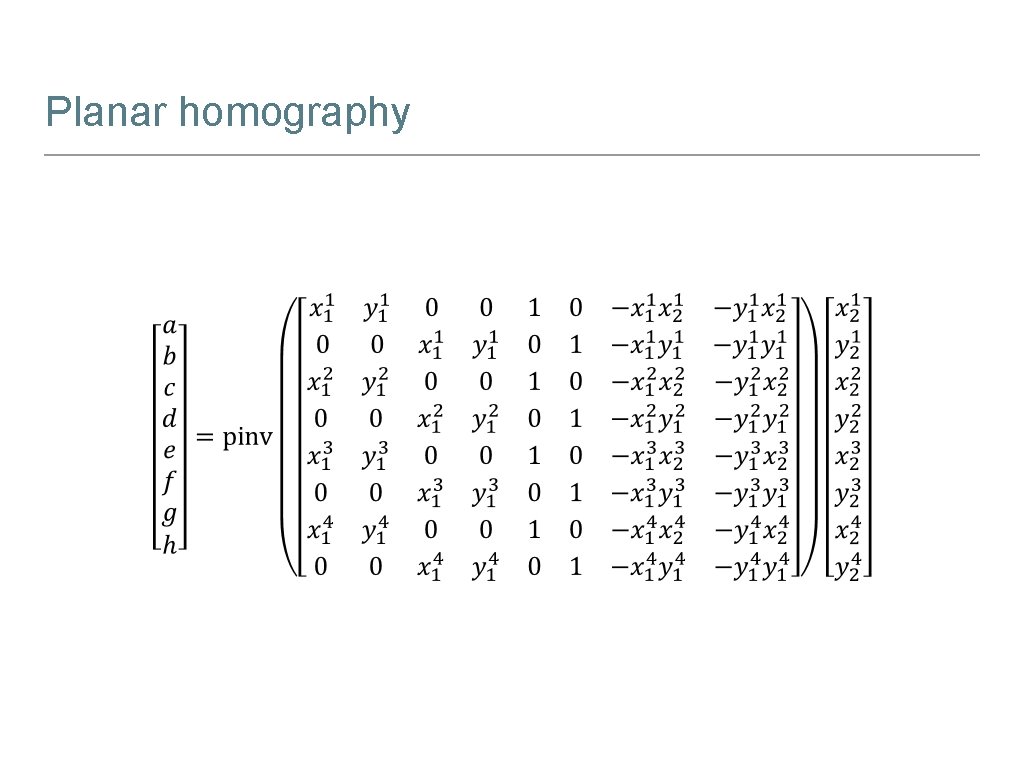
Planar homography • We got a 3 × 3 matrix, appropriate for the cases of points in the scene that lies on the same plane. We call this matrix Homography Matrix. • Once again the scale factor is arbitrary and ignorable. • Only 8 unique numbers left to be determined in the homography matrix. • Can be estimated from (at least) 4 world points and their corresponding image points.

Planar homography Pseudo Inverse

Planar homography Pseudo Inverse

Planar homography

Planar homography

Planar homography

Planar homography

Planar homography

Demo time!

The effect of virtual camera • Using the Homography matrix for dealing perspective distortions and other problematic cameras’ positions may be seen as projection of the handheld camera in the reality into a virtual camera which roles as a camera in which the result image of the homography is taken. • This virtual camera’s position is suitable for the actual perspective that we want to see the objects in the image.

The effect of virtual camera Virtual Camera Handled Camera

Planar homography - Some problems… • In most interesting images and cases, not all the points in the image are on the same plane. By wrapping the image according to the homography matrix, created for a specific plane, some distortions may occur regarding these points, and especially regarding edges in the image which connecting two planes in the world.

Planar homography - more uses

Planar homography - more uses

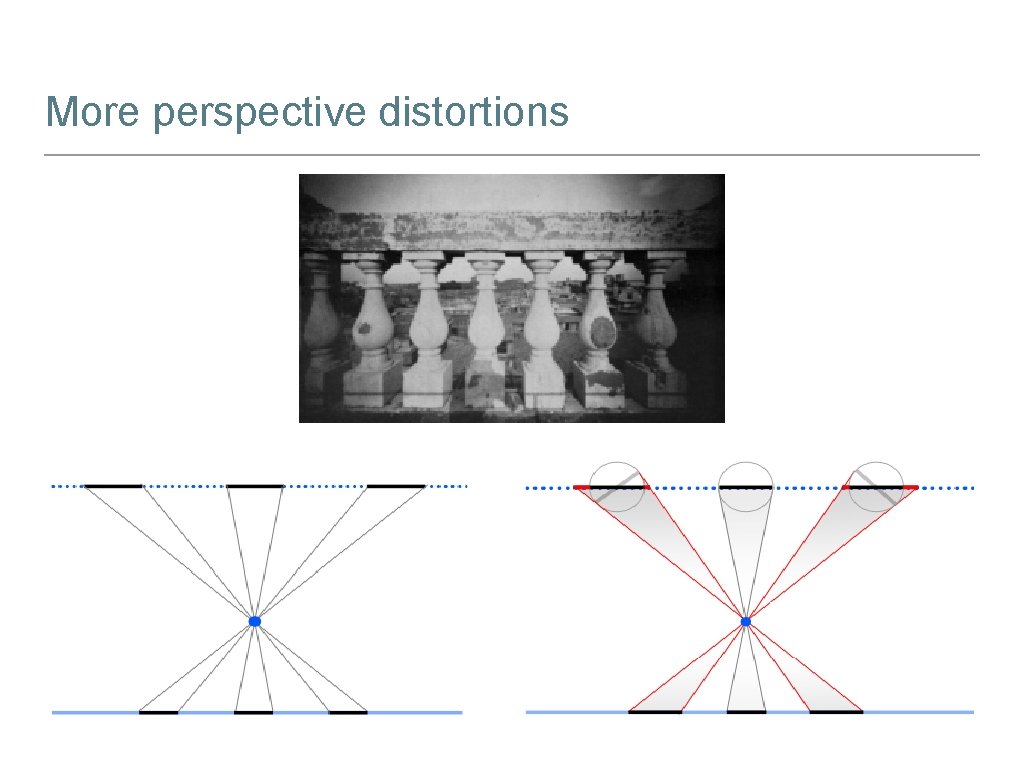
More perspective distortions • • The problem pointed initially by Da Vinci: • When we project some equal flat vertical objects, standing on a line parallel to the image plane, all these objects looks with the same length also in the projected 2 D image. • But if we use equal vertical cylindrical objects instead of the flat ones, under the same conditions, we notice that the exterior objects appear bigger. Important to note that this distortion has nothing to do with lens flaws.

More perspective distortions

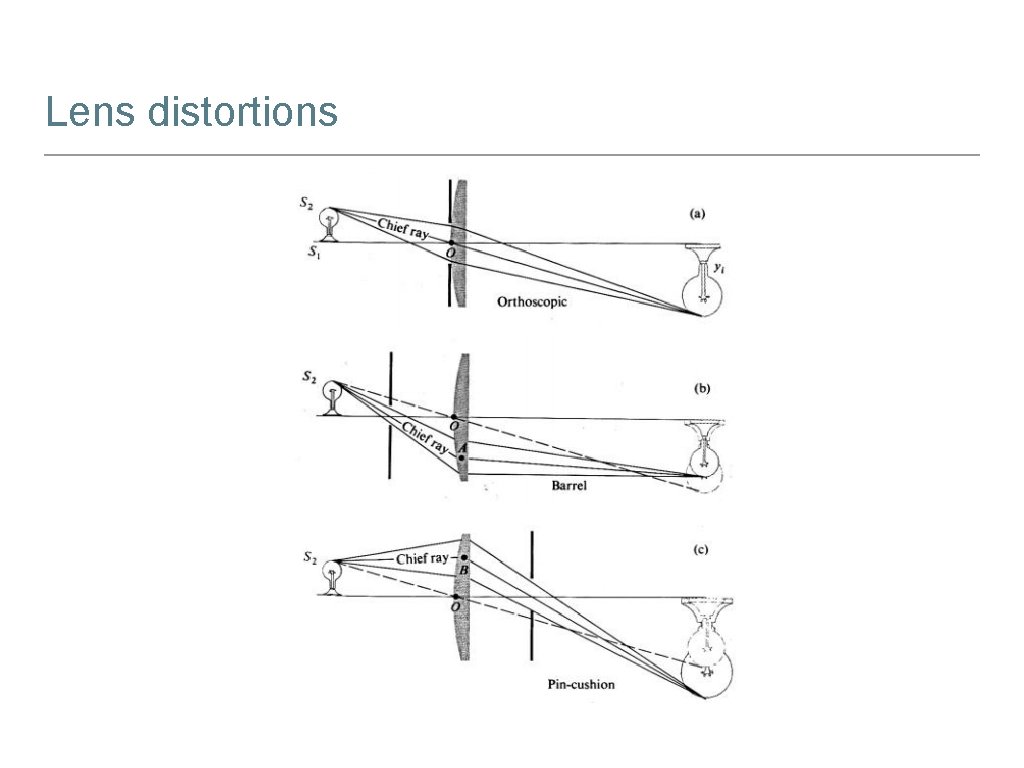
Lens distortions • Sometimes distortions in the images may stem from imperfect camera’s lens. • So far all the imaging models assume that cameras obeys a linear projection model, where straight lines in the world result in straight lines in the image. Unfortunately, many wide-angle lenses have noticeable radial distortion.

Lens distortions

Lens distortions • The coordinates in the observed images are displayed away from (Barrel) or towards (Pin-cushion) the image center by an amount proportional to their radial distance. Barrel distortion Pin-cushion distortion

Lens distortions

Lens distortions • Let be the pixel coordinates obtained after perspective division (from the homogeneous coordinates , but before scaling by focal length �� and shifting the optical centre ).

Lens distortions • Apply radial distortion according to the quartic model. �� 1 and �� 2 are called the radial distortion parameters.

Lens distortions • Compute the final pixel coordinates by applying focal length and translate image center.

Lens distortions - some exceptions • Fish-eye lens – produce strong visual distortion intended to create a wide panoramic or hemispherical image.

Lens distortions - some exceptions • • Anamorphic lenses – widely used in feature file production in order a wider range of aspect ratios could fit within a standard image sensor. These lens do not follow the radial distortion model we suggest. Instead, they can be thought of as inducing different vertical and horizontal scaling, i. e. non-square pixels. images from http: //www. red. com/learn/red-101/anamorphic-lenses

References • Szeliski: Ch. 2. 1. 3 -2. 1. 6, 6. 2, 6. 3 • cs. cornell. edu: http: //www. cs. cornell. edu/courses/cs 4670/2013 fa/lectures/lec 13_projection. pdf http: //www. cs. cornell. edu/courses/cs 4670/2013 fa/lectures/lec 14_projection. pdf http: //www. cs. cornell. edu/courses/cs 4670/2013 fa/lectures/lec 16_svm. pdf http: //www. cs. cornell. edu/courses/cs 4670/2013 fa/lectures/lec 17_svm 2. pdf • csail. mit. edu: http: //people. csail. mit. edu/torralba/courses/6. 869. computervision. htm • cs. haifa. ac. il/hagit: http: //cs. haifa. ac. il/hagit/courses/CP/Lectures/CP 11_Single. View. X 4. pdf • https: //www. youtube. com/watch? v=4 -th. Td. R 7 Blg • https: //www. youtube. com/watch? v=GVmbfy. Blods&spfreload=10 https: //www. youtube. com/watch? v=f. VJe. JMWZcq 8&spfreload=10