Overview of Web Ranking Algorithms HITS and Page

Overview of Web Ranking Algorithms: HITS and Page. Rank April 6, 2006 Presented by: Bill Eberle

Overview n n n Problem Web as a Graph HITS Page. Rank Comparison

Problem n n n Specific queries (scarcity problem). Broad-topic queries (abundance problem). Goal: to find the smallest set of “authoritative” sources.
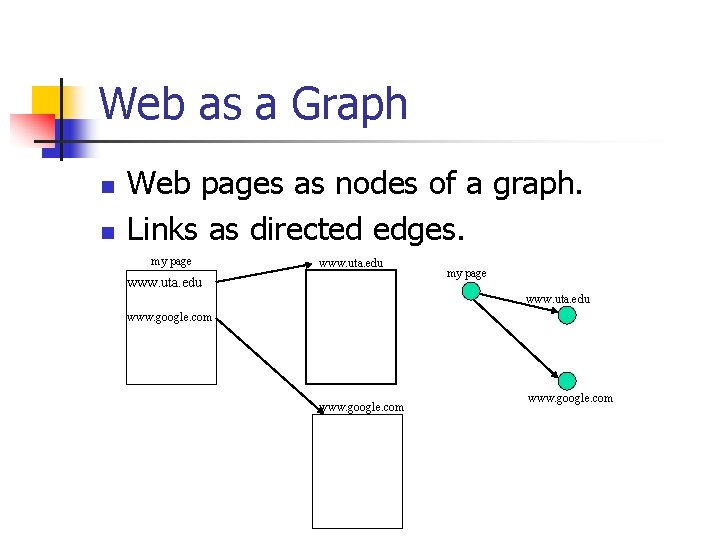
Web as a Graph n n Web pages as nodes of a graph. Links as directed edges. my page www. uta. edu www. google. com

Link Structure of the Web n n n Forward links (out-edges). Backward links (in-edges). Approximation of importance/quality: a page may be of high quality if it is referred to by many other pages, and by pages of high quality.

HITS n n HITS (Hyperlinked-Induced Topic Search) “Authoritative Sources in a Hyperlinked Environment”, Jon Kleinberg, Cornell University. 1998.

Authorities and Hubs n n Authority is a page which has relevant information about the topic. Hub is a page which has collection of links to pages about that topic. a 1 a 2 h a 3 a 4

Authorities and Hubs (cont. ) n n Good hubs are the ones that point to good authorities. Good authorities are the ones that are h pointed to by a good hubs. 1 1 h 2 a 2 h 3 a 4 h 5 a 6

Finding Authorities and Hubs n n First, construct a focused sub-graph of the www. Second, compute Hubs and Authorities from the sub-graph.
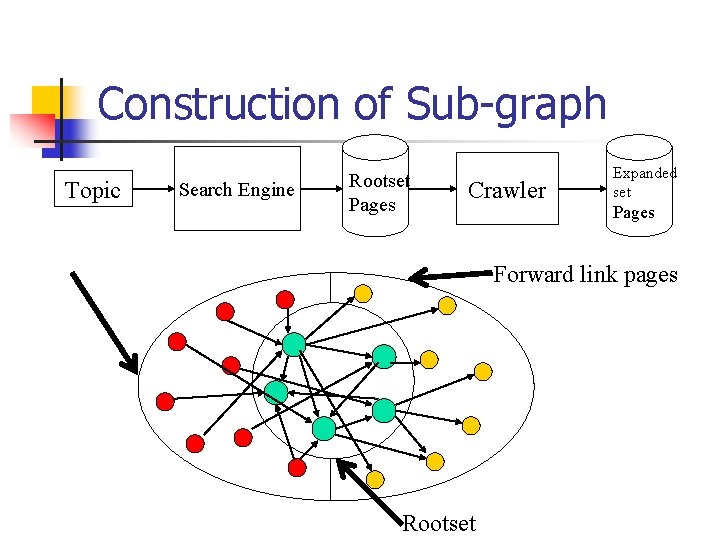
Construction of Sub-graph Topic Search Engine Rootset Pages Crawler Expanded set Pages Forward link pages Rootset
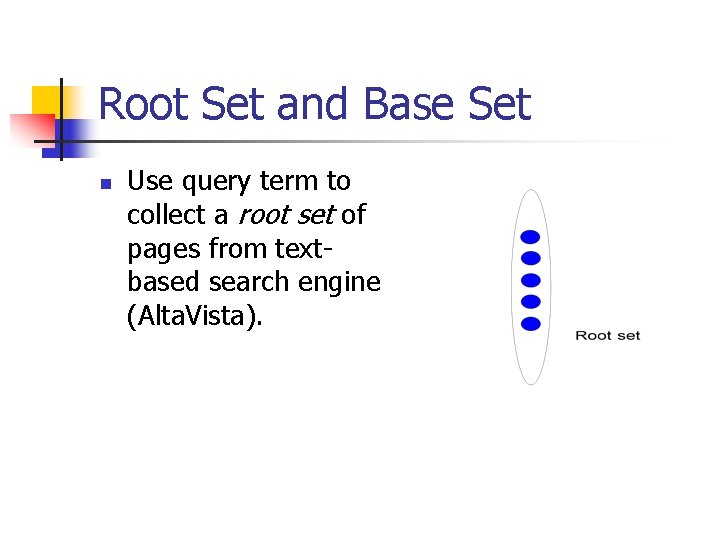
Root Set and Base Set n Use query term to collect a root set of pages from textbased search engine (Alta. Vista).
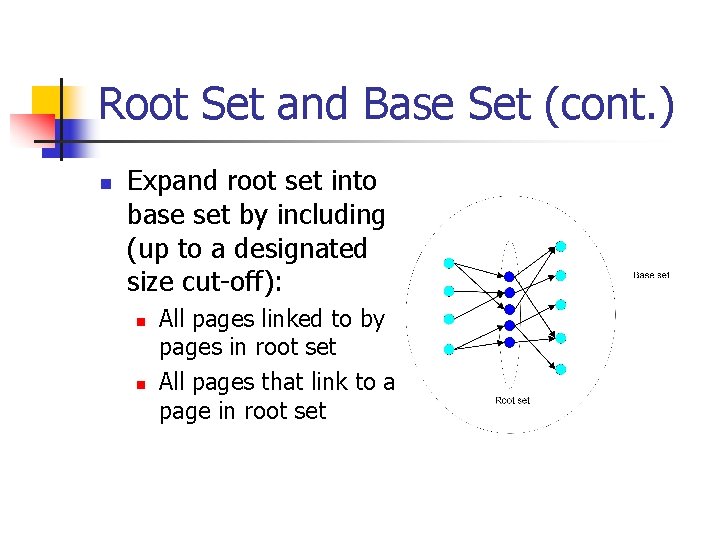
Root Set and Base Set (cont. ) n Expand root set into base set by including (up to a designated size cut-off): n n All pages linked to by pages in root set All pages that link to a page in root set

Hubs & Authorities Calculation n Iterative algorithm on Base Set: authority weights a(p), and hub weights h(p). n Set authority weights a(p) = 1, and hub weights h(p) = 1 for all p. n Repeat following two operations (and then re-normalize a and h to have unit norm): h(v 1) v 1 h(v 2) v 2 h(v 3) v 3 p p v 1 a(v 1) v 2 a(v 2) v 3 a(v 3)
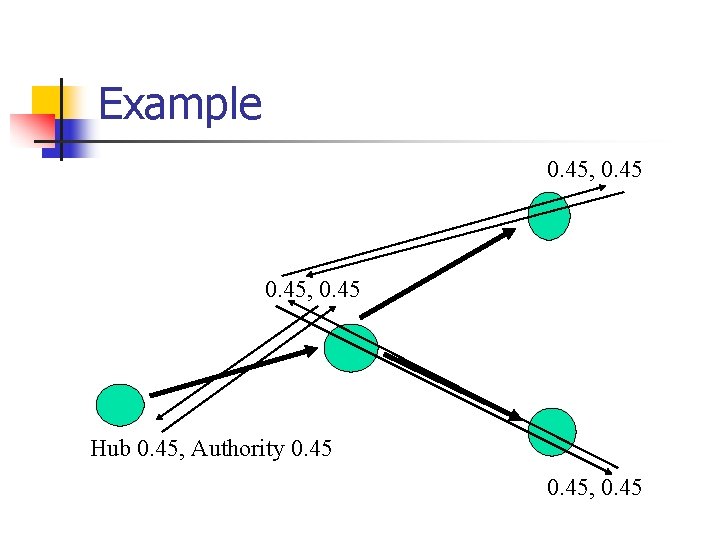
Example 0. 45, 0. 45 Hub 0. 45, Authority 0. 45, 0. 45
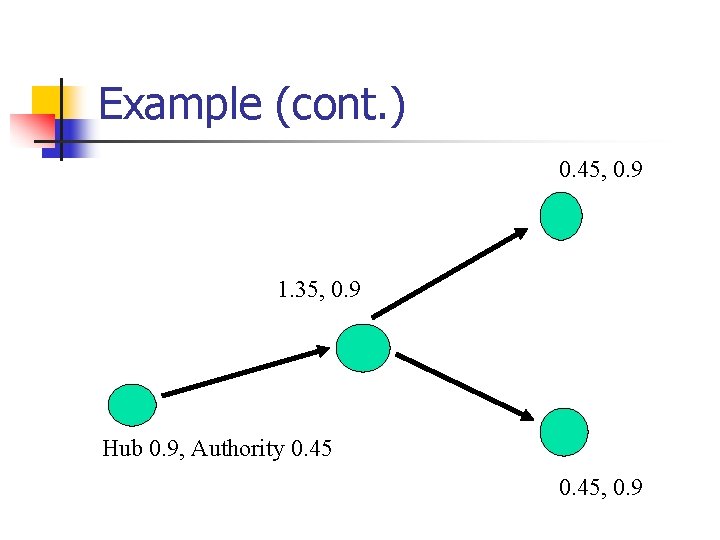
Example (cont. ) 0. 45, 0. 9 1. 35, 0. 9 Hub 0. 9, Authority 0. 45, 0. 9

Algorithmic Outcome n n n Applying iterative multiplication (power iteration) will lead to calculating eigenvector of any “non-degenerate” initial vector. Hubs and authorities as outcome of process. Principal eigenvector contains highest hub and authorities.

Results n n Although HITS is only link-based (it completely disregards page content) results are quite good in many tested queries. When the authors tested the query “search engines”: n n The algorithm returned Yahoo!, Excite, Magellan, Lycos, Alta. Vista However, none of these pages described themselves as a “search engine” (at the time of the experiment)

Issues n n n From narrow topic, HITS tends to end in more general one. Specific of hub pages - many links can cause algorithm drift. They can point to authorities in different topics. Pages from single domain / website can dominate result, if they point to one page - not necessarily a good authority.

Possible Enhancements n n n Use weighted sums for link calculation. Take advantage of “anchor text” - text surrounding link itself. Break hubs into smaller pieces. Analyze each piece separately, instead of whole hub page as one. Disregard or minimize influence of links inside one domain. IBM expanded HITS into Clever; not seen as viable real-time search engine.

Page. Rank n “The Page. Rank Citation Ranking: Bringing Order to the Web”, Lawrence Page and Sergey Brin, Stanford University. 1998.

Basic Idea n n Back-links coming from important pages convey more importance to a page. For example, if a web page has a link off the yahoo home page, it may be just one link but it is a very important one. A page has high rank if the sum of the ranks of its back-links is high. This covers both the case when a page has many back-links and when a page has a few highly ranked backlinks.

Definition n My page’s rank is equal to the sum of all the pages pointing to me.

Simplified Page. Rank Example n Rank(u) = Rank of page u , where c is a normalization constant (c < 1 to cover for pages with no outgoing links).

Expanded Definition n n n R(u): page rank of page u c: factor used for normalization (<1) Bu: set of pages pointing to u Nv: outbound links of v R(v): page rank of site v that points to u E(u): distribution of web pages that a random surfer periodically jumps (set to 0. 15)
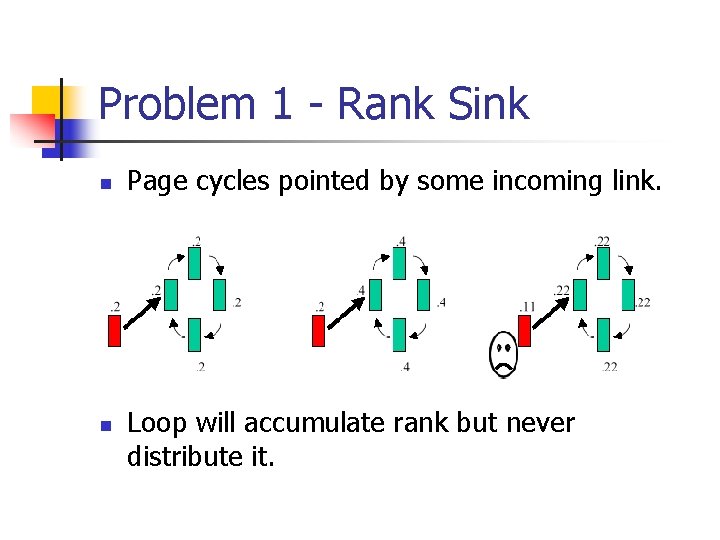
Problem 1 - Rank Sink n n Page cycles pointed by some incoming link. Loop will accumulate rank but never distribute it.
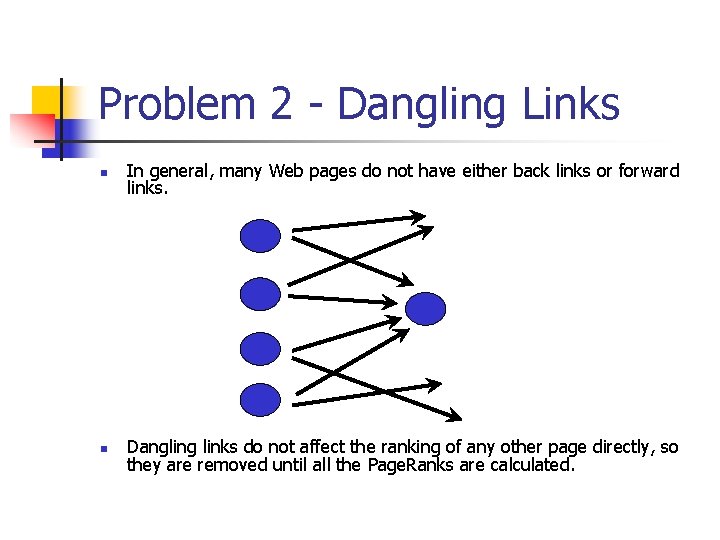
Problem 2 - Dangling Links n In general, many Web pages do not have either back links or forward links. n Dangling links do not affect the ranking of any other page directly, so they are removed until all the Page. Ranks are calculated.
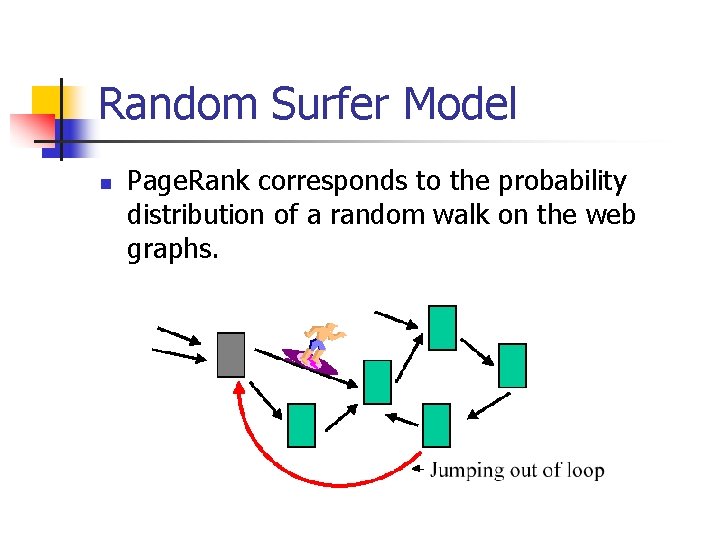
Random Surfer Model n Page. Rank corresponds to the probability distribution of a random walk on the web graphs.

Solution – Escape Term n n Escape term: E(u) can be thought of as the random surfer gets bored periodically and jumps to a different page – not staying in the loop forever. We term this E to be a vector over all the web pages that accounts for each page’s escape probability (user defined parameter).

Page. Rank Computation - initialize vector over web pages Loop: - new ranks sum of normalized backlink ranks - compute normalizing factor - add escape term - control parameter While - stop when converged
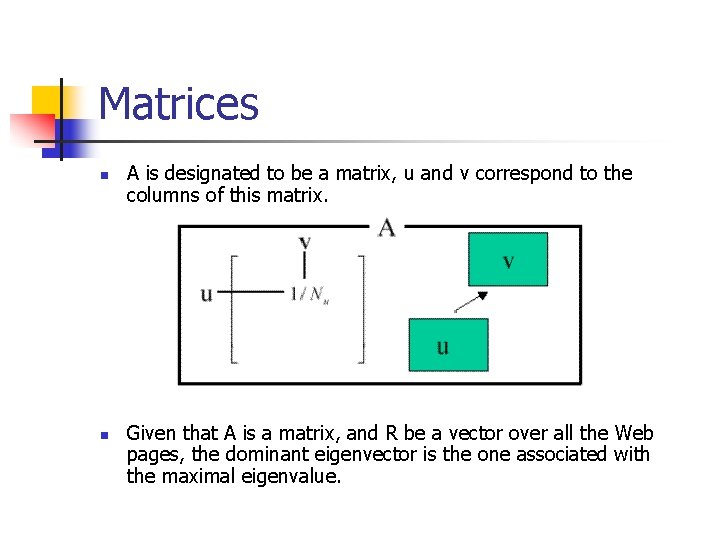
Matrices n n A is designated to be a matrix, u and v correspond to the columns of this matrix. Given that A is a matrix, and R be a vector over all the Web pages, the dominant eigenvector is the one associated with the maximal eigenvalue.
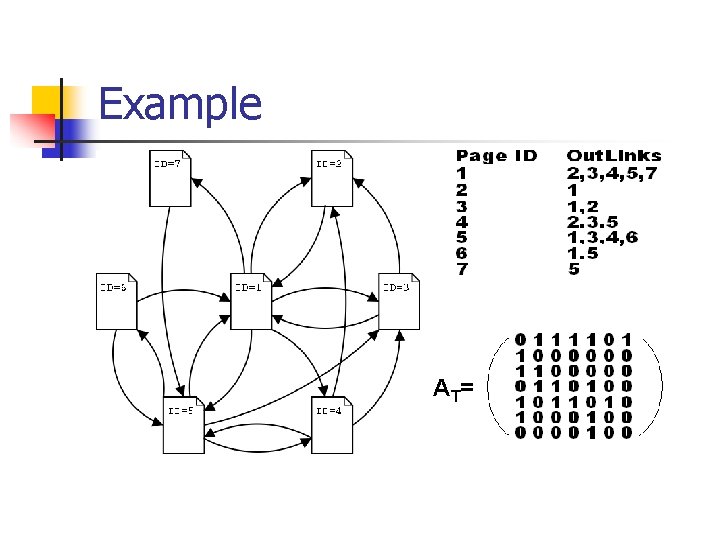
Example AT =
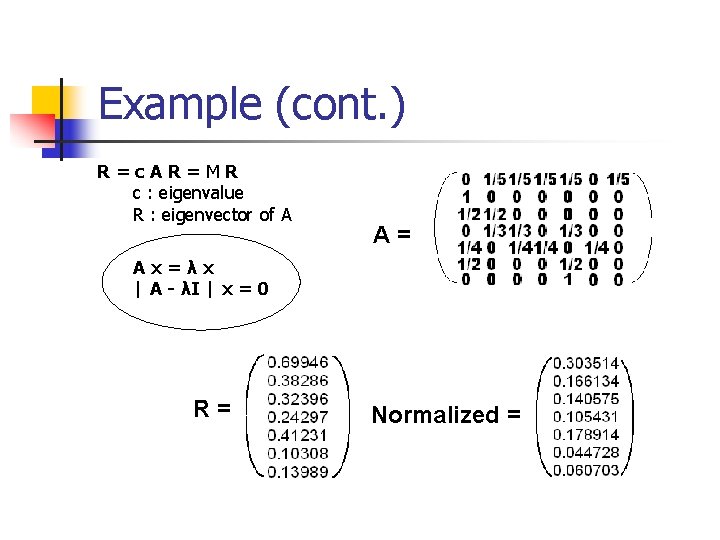
Example (cont. ) R=c. AR=MR c : eigenvalue R : eigenvector of A A= Ax=λx | A - λI | x = 0 R= Normalized =

Implementation 1. URL -> id 2. Store each hyperlink in a database. 3. Sort link structure by Parent id. 4. Remove dangling links. 5. Calculate the PR giving each page an initial value. 6. Iterate until convergence. 7. Add the dangling links.
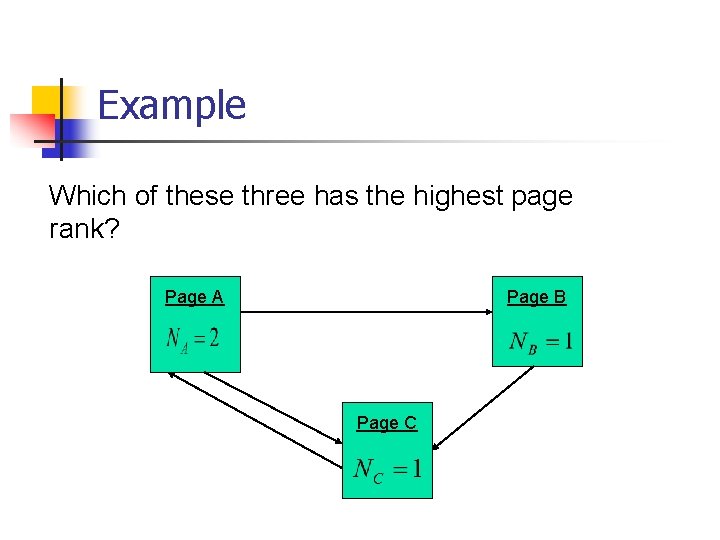
Example Which of these three has the highest page rank? Page A Page B Page C
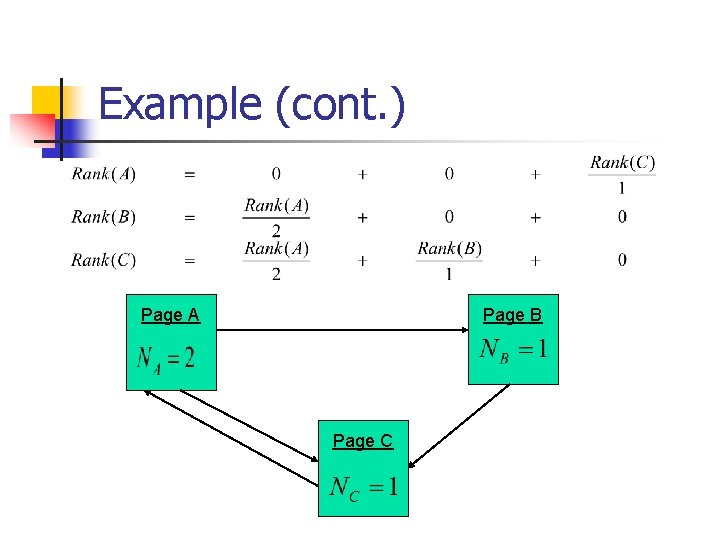
Example (cont. ) Page A Page B Page C

Example (cont. ) § Re-write the system of equations as a Matrix. Vector product. The Page. Rank vector is simply an eigenvector (scalar*vector = matrix*vector) of the coefficient matrix.
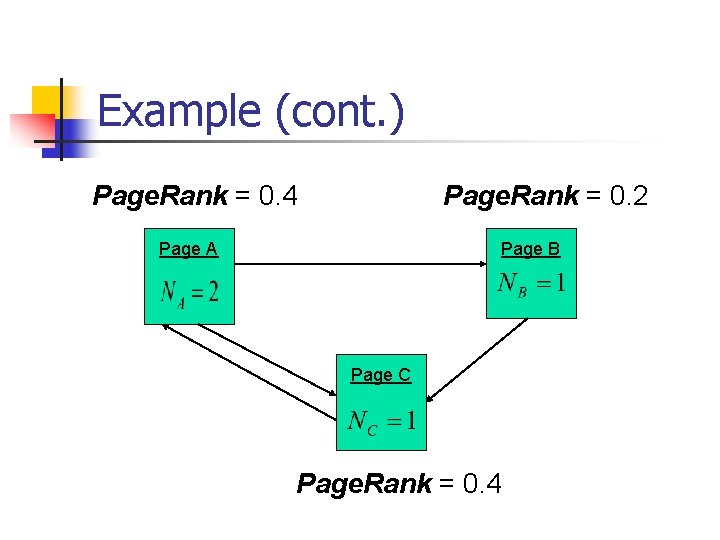
Example (cont. ) Page. Rank = 0. 4 Page. Rank = 0. 2 Page A Page B Page C Page. Rank = 0. 4
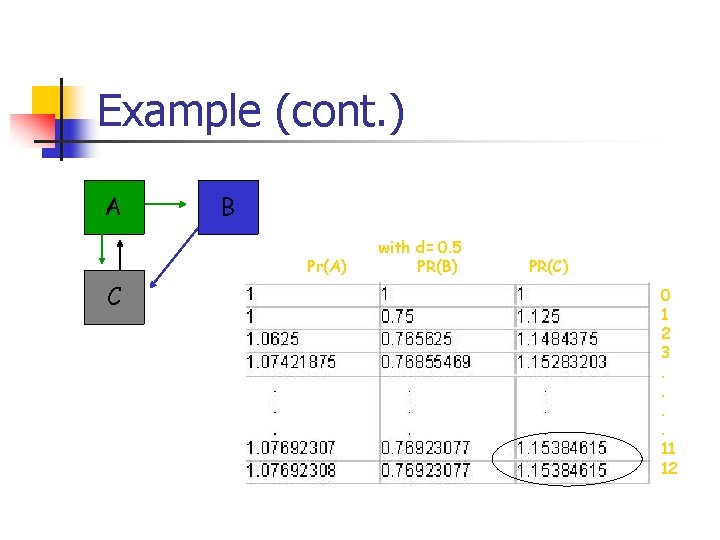
Example (cont. ) A B Pr(A) C with d= 0. 5 PR(B) PR(C) 0 1 2 3. . 11 12
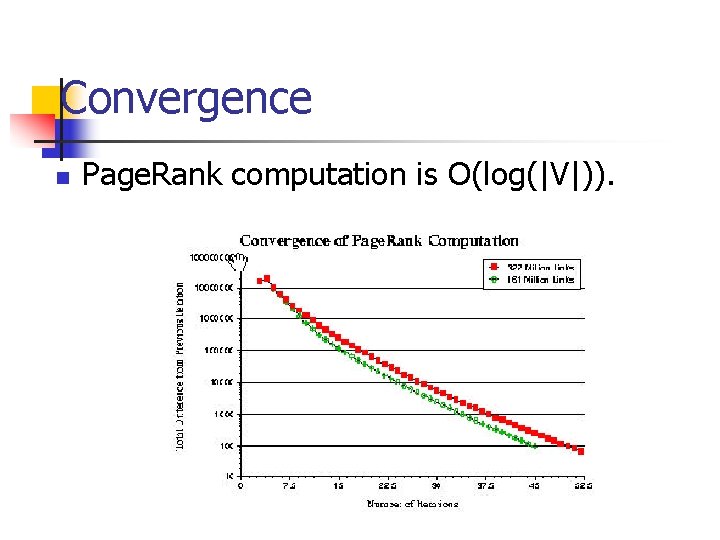
Convergence n Page. Rank computation is O(log(|V|)).

Other Applications n n Help user decide if a site is trustworthy. Estimate web traffic. Spam detection and prevention. Predict citation counts.

Issues n n n Users are not random walkers. Starting point distribution (actual usage data as starting vector). Bias towards main pages. Linkage spam. No query specific rank.

Page. Rank vs. HITS n Page. Rank (Google) n n n computed for all web pages stored in the database prior to the query computes authorities only Trivial and fast to compute n HITS (CLEVER) n n n performed on the set of retrieved web pages for each query computes authorities and hubs easy to compute, but real-time execution is hard

References n n “Authoritative Sources in a Hyperlinked Environment”, Jon Kleinberg, Cornell University. 1998. “The Page. Rank Citation Ranking: Bringing Order to the Web”, Lawrence Page and Sergey Brin, Stanford University. 1998.
- Slides: 43