Overview of JLab Nuclear Physics Program General Introduction

Overview of JLab Nuclear Physics Program • General Introduction: Why Electron Scattering? • 15+ years of JLab Experiments: Some Highlights • The Role of Quarks in Nuclear Physics CEBAF’s Original Mission Statement • Nucleon and Pion Elastic Form Factors and Transition Form Factors to Nucleon Excited States • The Strange Quark Content of the Proton • The Onset of the Quark Parton Model: The Quark-Hadron Transition • Deep Exclusive Reactions and Semi-Inclusive Reactions: Beyond One-Dimensional Substructure of Nucleons Constraints on Angular Momentum • On to the 12 Ge. V Program!

Cool Facts about QCD and Nuclei Did you know that … ? • If an atom was the size of a football field, the (atomic) nucleus would be about the size of a marble. • Despite its tiny dimensions, the nucleus accounts for 99. 9% of an atom’s mass. • Protons and neutrons swirl in a heavy atomic nucleus with speeds of up to some ¾ of c. More commonly, their speed is some ¼ the speed of light. The reason is because they are “strong-forced” to reside in a small space. • Quarks (and gluons) are “confined” to the even smaller space inside protons and neutrons. Because of this, they swirl around with the speed of light.

Cool Facts about QCD and Nuclei Did you know that … ? • The strong force is so strong, that you can never find one quark alone (this is called “confinement”). • When pried even a little apart, quarks experience ten tons of force pulling them together again. • Quarks and gluons jiggle around at nearly lightspeed, and extra gluons and quark/anti-quark pairs pop into existence one moment to disappear the next. • It is this flurry of activity, fueled by the energy of the gluons, that generates nearly all the mass of protons and neutrons, and thus ultimately of all the matter we see. • 99% of your mass is due to this stored energy. • Even the QCD “vacuum” is not truly empty. Long-distance gluonic fluctuations are an integral part. Quarks have small mass themselves, but attain an effective larger mass due to the fact that they attract these gluonic fluctuations around them M(up) + M(down) ~ 10 Me. V << M(proton)

Cool Facts about QCD and Nuclei Did you know that … ? • Nuclear physicists are trying to answer how basic properties like mass, shape, and spin come about from the flood of gluons, quark/anti-quark pairs, and a few everpresent quarks • A small fraction of the force between quarks and gluons “leaks out” of protons and neutrons, and binds them together to form tiny nuclei. The long-range part of this process can be well described as if protons and neutrons exchange pions. • Nuclear physicists are only now starting to understand how this “leakage” occurs, and how it results in the impressive variety of nuclei found in nature. • A nucleus consisting of some 100 protons and 150 neutrons can be the same size as one with 3 protons and 8 neutrons.
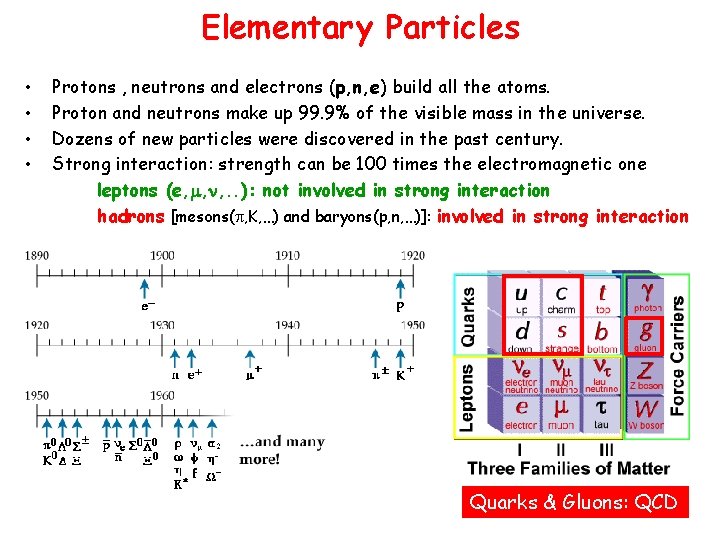
Elementary Particles • • Protons , neutrons and electrons (p, n, e) build all the atoms. Proton and neutrons make up 99. 9% of the visible mass in the universe. Dozens of new particles were discovered in the past century. Strong interaction: strength can be 100 times the electromagnetic one leptons (e, m, n, . . ): not involved in strong interaction hadrons [mesons( , K, …) and baryons(p, n, …)]: involved in strong interaction Quarks & Gluons: QCD

The Structure of the Proton Naïve Quark Model: proton = uud (valence quarks) QCD: proton = uud + uu + dd + ss + … The proton sea has a non-trivial structure: u ≠ d The proton is far more than just its up + down (valence) quark structure Nuclear physicists are trying to answer how basic properties like mass, shape, and spin come about from the flood of gluons, quark/anti-quark pairs, and a few ever-present quarks.
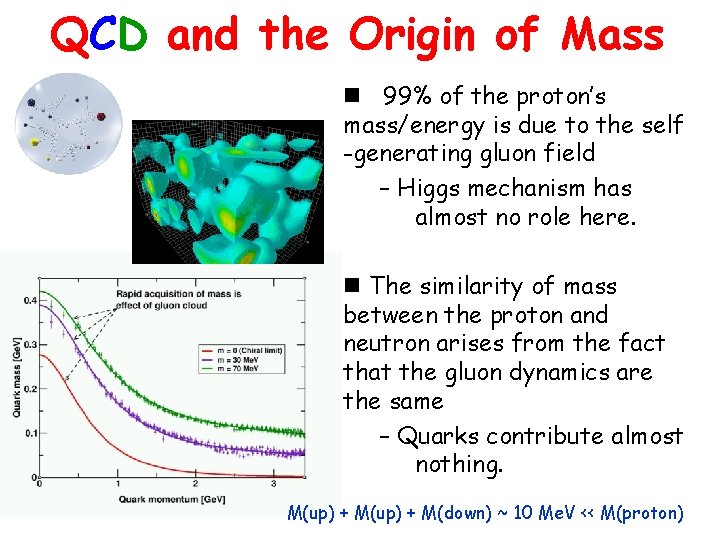
QCD and the Origin of Mass n 99% of the proton’s mass/energy is due to the self -generating gluon field – Higgs mechanism has almost no role here. n The similarity of mass between the proton and neutron arises from the fact that the gluon dynamics are the same – Quarks contribute almost nothing. M(up) + M(down) ~ 10 Me. V << M(proton)

QCD and Nuclei Gluons mediate the strong (color) force, just like photons mediate the electromagnetic force, but … gluons interact with themselves … which gives QCD unique properties QCD Lagrangian: quarks and gluons Nuclear Physics Model is an effective (but highly successful!) model using free nucleons and mesons as degrees of freedom.

Electron Scattering Electrons as probe of nuclear structure have some distinct advantages over other probes like hadrons or -rays: • The interaction between the electron and the nucleus is known; it is the electromagnetic interaction with the charge r and the current J of the nucleus: Vint = rf + J. A, where f and A are the scalar and vector potentials generated by the electron. • The interaction is weak, so that in almost all cases it can be treated in the “one-photon exchange approximation” (OPEA), i. e. , two-step processes (twophoton exchange) are small. The exception is charge elastic scattering of the Coulomb field of a heavy-Z nucleus. • The energy ( ) and linear momentum (q) transferred to the nucleus in the scattering process can be varied independently from each other. This is very important, as for a certain |q| one effectively measures a Fourier component of r or J. By varying |q| all Fourier components can be determined and from these the radial dependence of r and J can be reconstructed. • Because the photon has no charge, only the J. A interaction plays a role, leading to magnetic Ml and electric El transitions. In electron scattering, one can also have charge Cl transitions.

Electron Scattering Electron scattering has also some disadvantages: • The interaction is weak, so cross sections are small, but one can use high electron beam currents and thick targets. • Neutrons are less accessible than protons, since they do not have a net electric charge. • Because electrons are very light particles, they easily emit radiation (socalled Bremsstrahlung). This gives rise to radiative tails, with often large corrections for these processes.
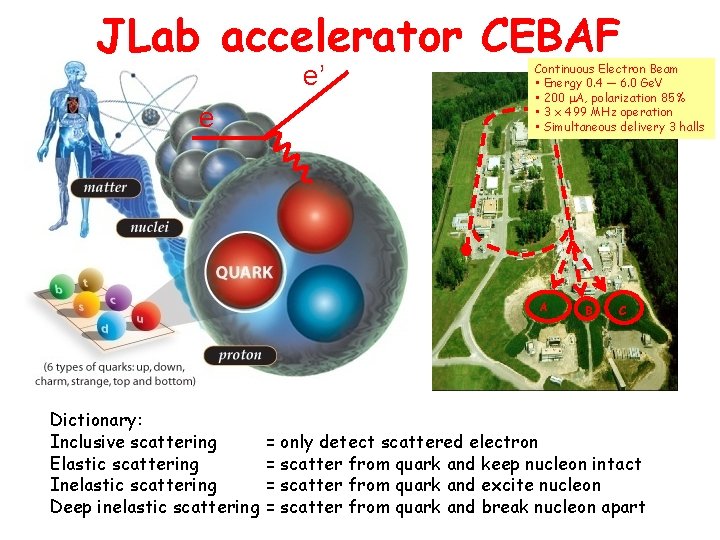
JLab accelerator CEBAF e’ e Continuous Electron Beam • Energy 0. 4 ─ 6. 0 Ge. V • 200 m. A, polarization 85% • 3 x 499 MHz operation • Simultaneous delivery 3 halls A Dictionary: Inclusive scattering Elastic scattering Inelastic scattering Deep inelastic scattering B C = only detect scattered electron = scatter from quark and keep nucleon intact = scatter from quark and excite nucleon = scatter from quark and break nucleon apart
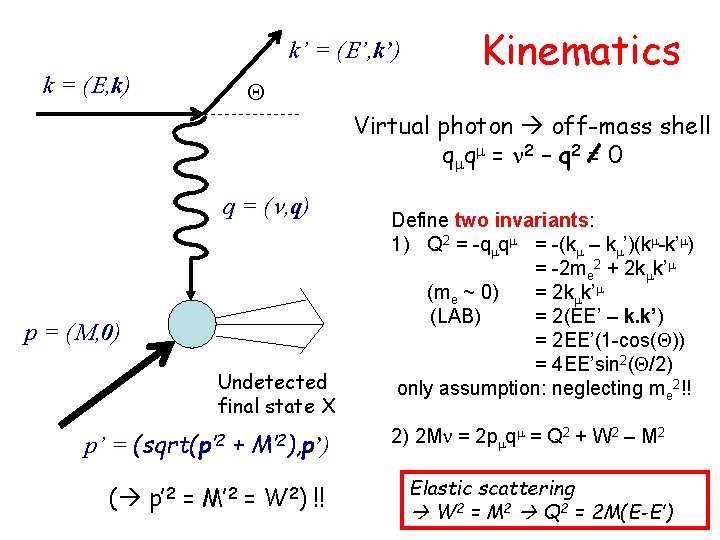
k’ = (E’, k’) k = (E, k) Q Kinematics Virtual photon off-mass shell qm qm = n 2 – q 2 = 0 q = (n, q) p = (M, 0) Undetected final state X p’ = (sqrt(p’ 2 + M’ 2), p’) ( p’ 2 = M’ 2 = W 2) !! Define two invariants: 1) Q 2 = -qmqm = -(km – km’)(km-k’m) = -2 me 2 + 2 kmk’m (me ~ 0) = 2 kmk’m (LAB) = 2(EE’ – k. k’) = 2 EE’(1 -cos(Q)) = 4 EE’sin 2(Q/2) only assumption: neglecting me 2!! 2) 2 Mn = 2 pmqm = Q 2 + W 2 – M 2 Elastic scattering W 2 = M 2 Q 2 = 2 M(E-E’)
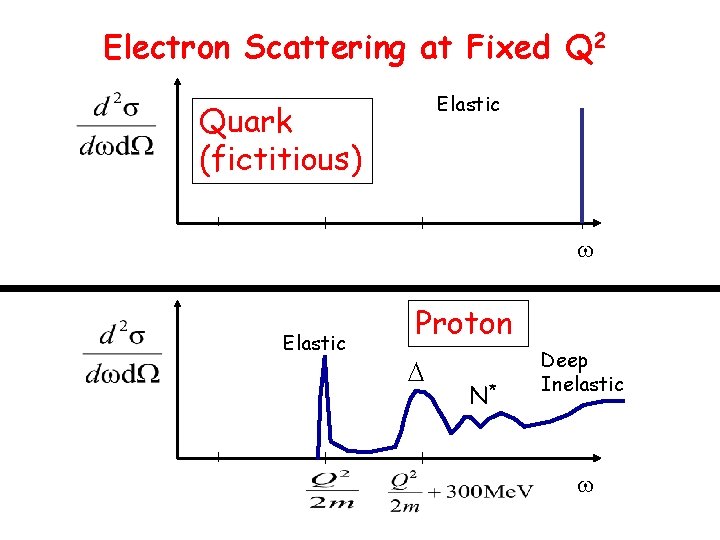
Electron Scattering at Fixed Q 2 Elastic Quark (fictitious) Elastic Proton N* Deep Inelastic
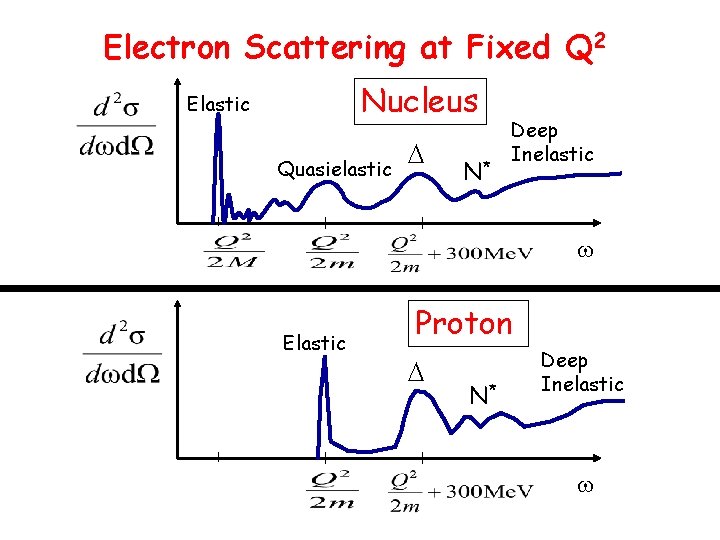
Electron Scattering at Fixed Q 2 Nucleus Elastic Quasielastic N* Deep Inelastic Elastic Proton N* Deep Inelastic
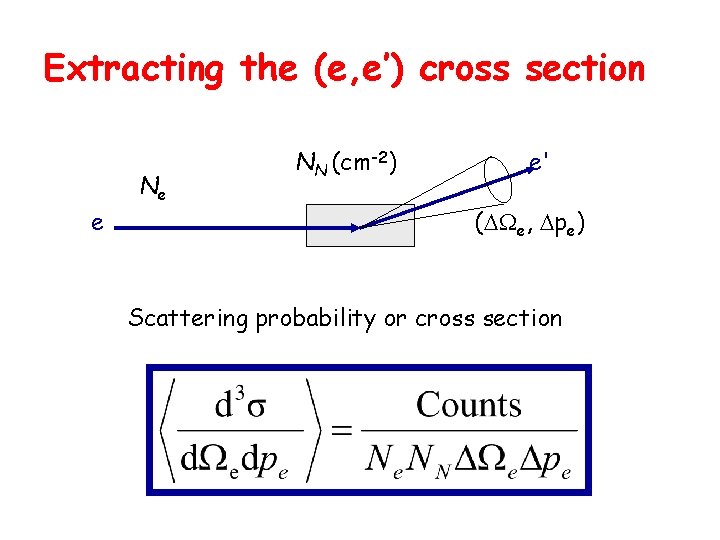
Extracting the (e, e’) cross section e Ne NN (cm-2) e' ( e, pe) Scattering probability or cross section
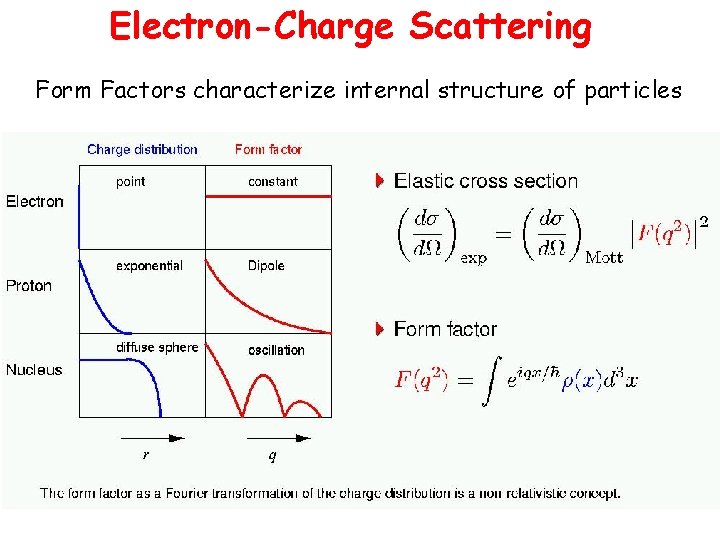
Electron-Charge Scattering Form Factors characterize internal structure of particles
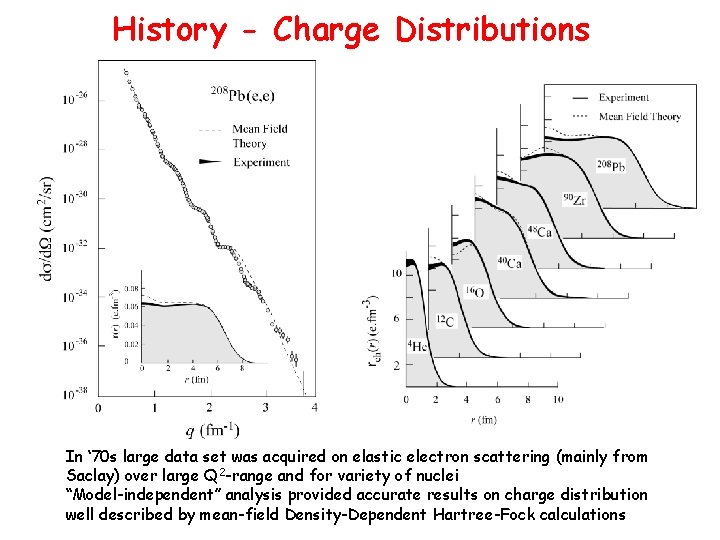
History - Charge Distributions In ‘ 70 s large data set was acquired on elastic electron scattering (mainly from Saclay) over large Q 2 -range and for variety of nuclei “Model-independent” analysis provided accurate results on charge distribution well described by mean-field Density-Dependent Hartree-Fock calculations
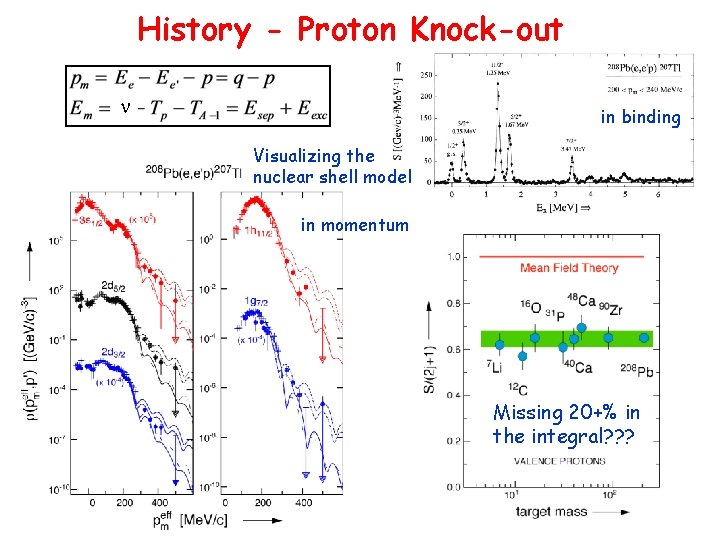
History - Proton Knock-out n in binding Visualizing the nuclear shell model in momentum Missing 20+% in the integral? ? ?
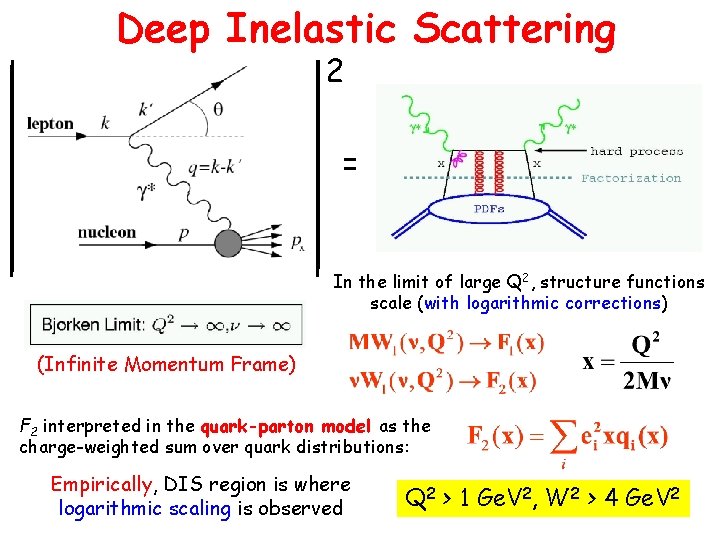
Deep Inelastic Scattering 2 = In the limit of large Q 2, structure functions scale (with logarithmic corrections) (Infinite Momentum Frame) F 2 interpreted in the quark-parton model as the charge-weighted sum over quark distributions: Empirically, DIS region is where logarithmic scaling is observed Q 2 > 1 Ge. V 2, W 2 > 4 Ge. V 2
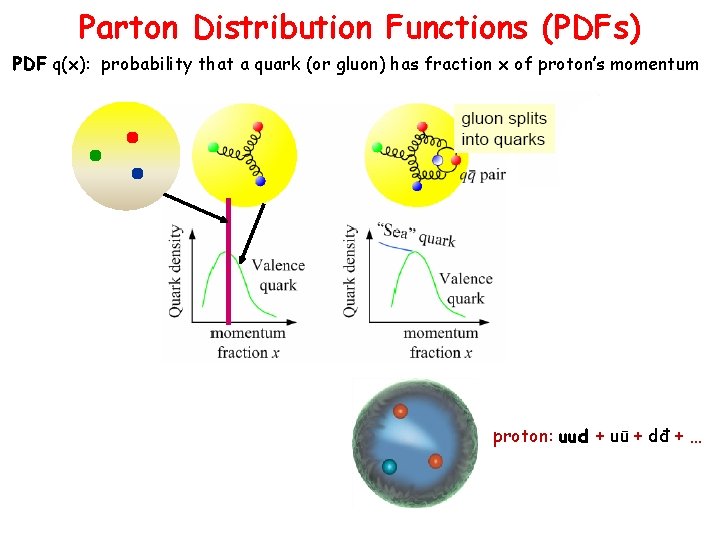
Parton Distribution Functions (PDFs) PDF q(x): probability that a quark (or gluon) has fraction x of proton’s momentum proton: uud + uū + dđ + …
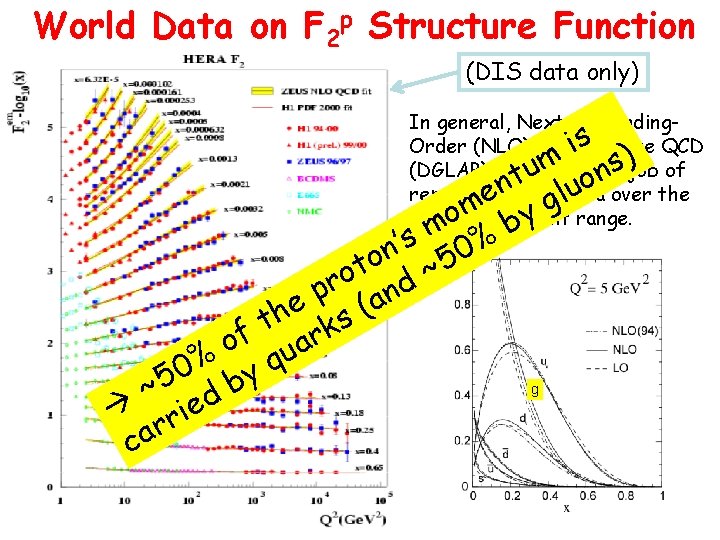
World Data on F 2 p Structure Function (DIS data only) In general, Next-to-Leading. Order (NLO) perturbative is ) QCD m s job of (DGLAP) fits do a good u n t o over the n the ldata u reproducing e om by g range. full measurement m s ’ % n 0 o 5 t ~ o r nd p e s (a h t k f r o ua % yq 0 ~5 d b rie r a c g

CEBAF’s Original Mission Statement Key Mission and Principal Focus (1987): The study of the largely unexplored transition between the nucleon-meson and the quark-gluon descriptions of nuclear matter. The Role of Quarks in Nuclear Physics Related Areas of Study: • Do individual nucleons change their size, shape, and quark structure in the nuclear medium? • How do nucleons cluster in the nuclear medium? • What are the properties of the force which binds quarks into nucleons and nuclei at distances where this force is strong and the quark confinement mechanism is important? Pushing the Limits of the Standard Model of Nuclear Physics Charge and Magnetization in Nucleons and Pions The Onset of the Parton Model

Halls A/B/C Base Equipment Hall A (2 HRS) Hall C (SOS/HMS) Hall B (CLAS)

Hall B - CLAS (forward carriage and side clamshells retracted) CLAS has more than 38, 000 readout channels Panel 4 TOF Large angle EC Panel 2 & 3 TOF Panel 1 TOF Region 3 drift chamber Cerenkov & Forward angle EC CLAS Overview, B. Mecking & staff, collaborators, NIM A 503 (2003) 513

Ancillary Equipment and Experiment-Specific Apparatus 2006 2002 -2007 GEn Electron Channel Setup 2004 DVCS Proton Array G 0 Setup 2005 BONUS RTPC Detector 2005 ENGE/HKS Setup

CEBAF’s Original Mission Statement Key Mission and Principal Focus (1987): The study of the largely unexplored transition between the nucleon-meson and the quark-gluon descriptions of nuclear matter. The Role of Quarks in Nuclear Physics Related Areas of Study: • Do individual nucleons change their size, shape, and quark structure in the nuclear medium? • How do nucleons cluster in the nuclear medium? • What are the properties of the force which binds quarks into nucleons and nuclei at distances where this force is strong and the quark confinement mechanism is important? Pushing the Limits of the Standard Model of Nuclear Physics Charge and Magnetization in Nucleons and Pions The Onset of the Parton Model
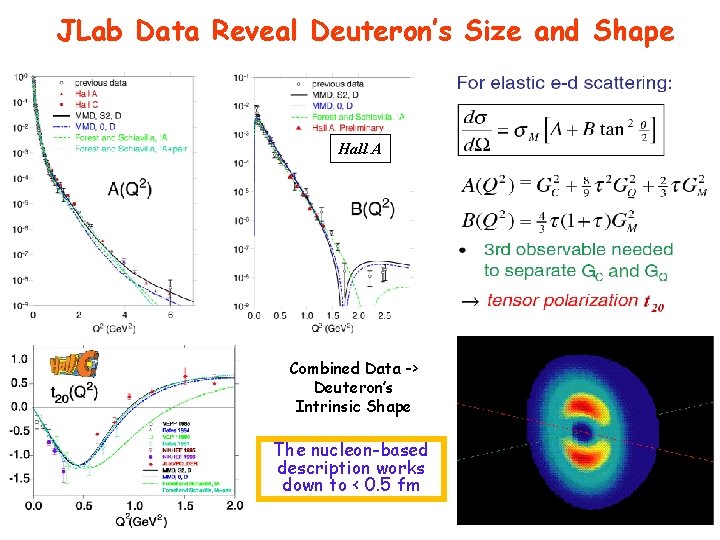
JLab Data Reveal Deuteron’s Size and Shape Hall A Combined Data -> Deuteron’s Intrinsic Shape The nucleon-based description works down to < 0. 5 fm
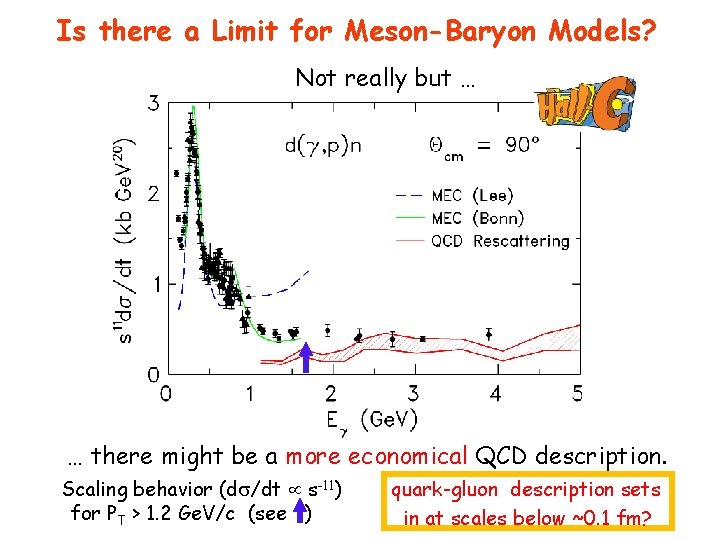
Is there a Limit for Meson-Baryon Models? Not really but … … there might be a more economical QCD description. Scaling behavior (d /dt s-11) for PT > 1. 2 Ge. V/c (see ) quark-gluon description sets in at scales below ~0. 1 fm?

CEBAF’s Original Mission Statement Key Mission and Principal Focus (1987): The study of the largely unexplored transition between the nucleon-meson and the quark-gluon descriptions of nuclear matter. The Role of Quarks in Nuclear Physics Related Areas of Study: • Do individual nucleons change their size, shape, and quark structure in the nuclear medium? • How do nucleons cluster in the nuclear medium? • What are the properties of the force which binds quarks into nucleons and nuclei at distances where this force is strong and the quark confinement mechanism is important? Pushing the Limits of the Standard Model of Nuclear Physics Charge and Magnetization in Nucleons and Pions The Onset of the Parton Model
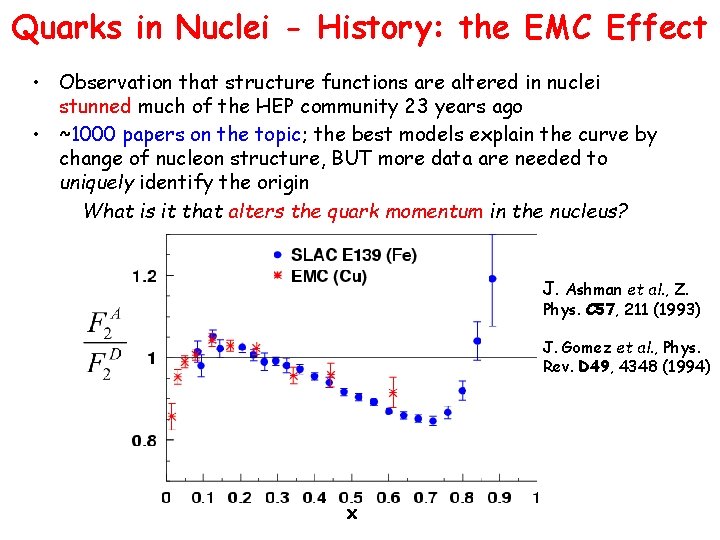
Quarks in Nuclei - History: the EMC Effect • Observation that structure functions are altered in nuclei stunned much of the HEP community 23 years ago • ~1000 papers on the topic; the best models explain the curve by change of nucleon structure, BUT more data are needed to uniquely identify the origin What is it that alters the quark momentum in the nucleus? J. Ashman et al. , Z. Phys. C 57, 211 (1993) J. Gomez et al. , Phys. Rev. D 49, 4348 (1994) x
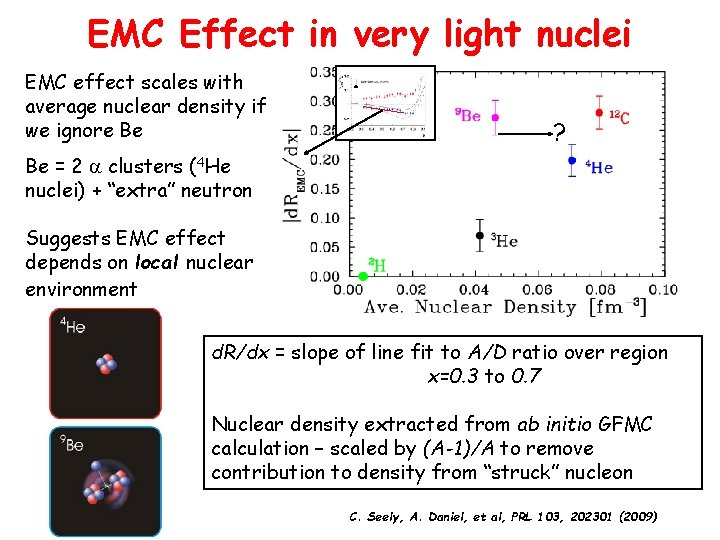
EMC Effect in very light nuclei EMC effect scales with average nuclear density if we ignore Be ? Be = 2 clusters (4 He nuclei) + “extra” neutron Suggests EMC effect depends on local nuclear environment d. R/dx = slope of line fit to A/D ratio over region x=0. 3 to 0. 7 Nuclear density extracted from ab initio GFMC calculation – scaled by (A-1)/A to remove contribution to density from “struck” nucleon C. Seely, A. Daniel, et al, PRL 103, 202301 (2009)

CEBAF’s Original Mission Statement Key Mission and Principal Focus (1987): The study of the largely unexplored transition between the nucleon-meson and the quark-gluon descriptions of nuclear matter. The Role of Quarks in Nuclear Physics Related Areas of Study: • Do individual nucleons change their size, shape, and quark structure in the nuclear medium? • How do nucleons cluster in the nuclear medium? • What are the properties of the force which binds quarks into nucleons and nuclei at distances where this force is strong and the quark confinement mechanism is important? Pushing the Limits of the Standard Model of Nuclear Physics The Onset of the Parton Model Use the Nuclear Arena to Study QCD
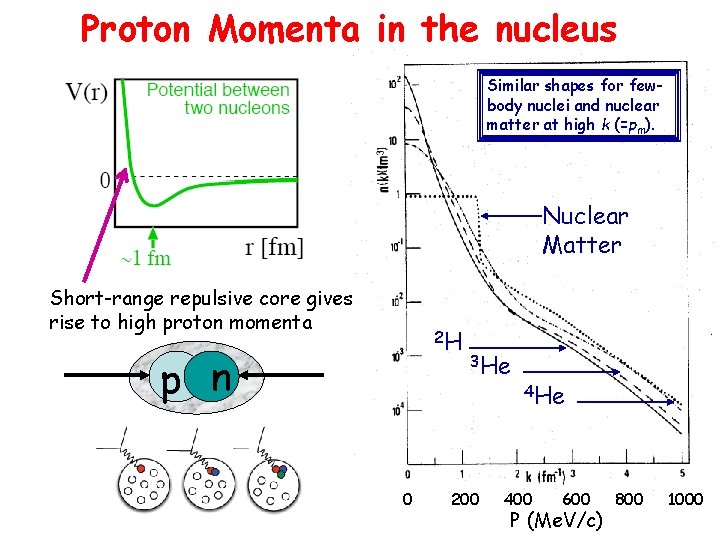
Proton Momenta in the nucleus Similar shapes for fewbody nuclei and nuclear matter at high k (=pm). Nuclear Matter Short-range repulsive core gives rise to high proton momenta 2 H p n 0 3 He 200 4 He 400 600 P (Me. V/c) 800 1000
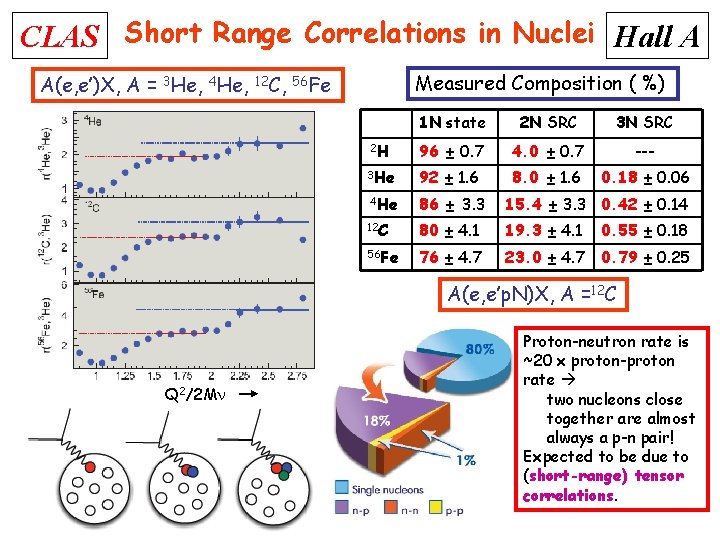
CLAS Short Range Correlations in Nuclei Hall A A(e, e’)X, A = 3 He, 4 He, Measured Composition ( %) 12 C, 56 Fe 1 N state 2 N SRC 3 N SRC 2 H 96 ± 0. 7 4. 0 ± 0. 7 --- 3 He 92 ± 1. 6 8. 0 ± 1. 6 0. 18 ± 0. 06 4 He 86 ± 3. 3 15. 4 ± 3. 3 0. 42 ± 0. 14 12 C 80 ± 4. 1 19. 3 ± 4. 1 0. 55 ± 0. 18 56 Fe 76 ± 4. 7 23. 0 ± 4. 7 0. 79 ± 0. 25 A(e, e’p. N)X, A =12 C Q 2/2 Mn Proton-neutron rate is ~20 x proton-proton rate two nucleons close together are almost always a p-n pair! Expected to be due to (short-range) tensor correlations.
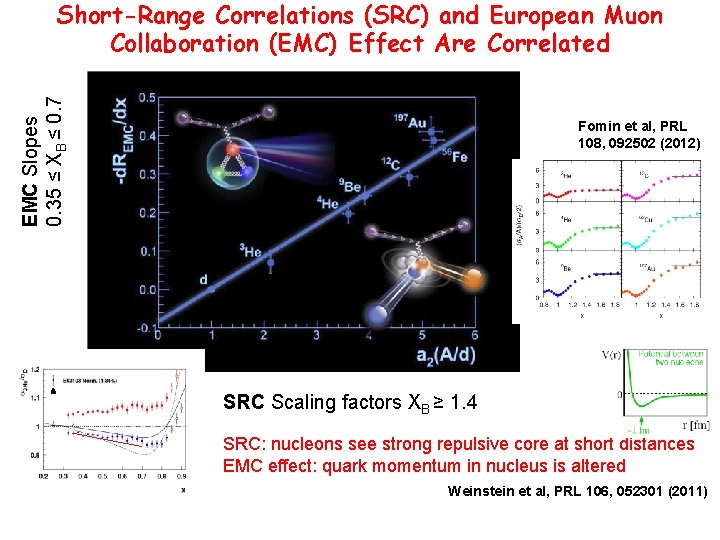
EMC Slopes 0. 35 ≤ XB ≤ 0. 7 Short-Range Correlations (SRC) and European Muon Collaboration (EMC) Effect Are Correlated Fomin et al, PRL 108, 092502 (2012) SRC Scaling factors XB ≥ 1. 4 SRC: nucleons see strong repulsive core at short distances EMC effect: quark momentum in nucleus is altered Weinstein et al, PRL 106, 052301 (2011)

CEBAF’s Original Mission Statement Key Mission and Principal Focus (1987): The study of the largely unexplored transition between the nucleon-meson and the quark-gluon descriptions of nuclear matter. The Role of Quarks in Nuclear Physics Related Areas of Study: • Do individual nucleons change their size, shape, and quark structure in the nuclear medium? • How do nucleons cluster in the nuclear medium? • What are the properties of the force which binds quarks into nucleons and nuclei at distances where this force is strong and the quark confinement mechanism is important? Pushing the Limits of the Standard Model of Nuclear Physics Charge and Magnetization in Nucleons and Pions The Onset of the Parton Model
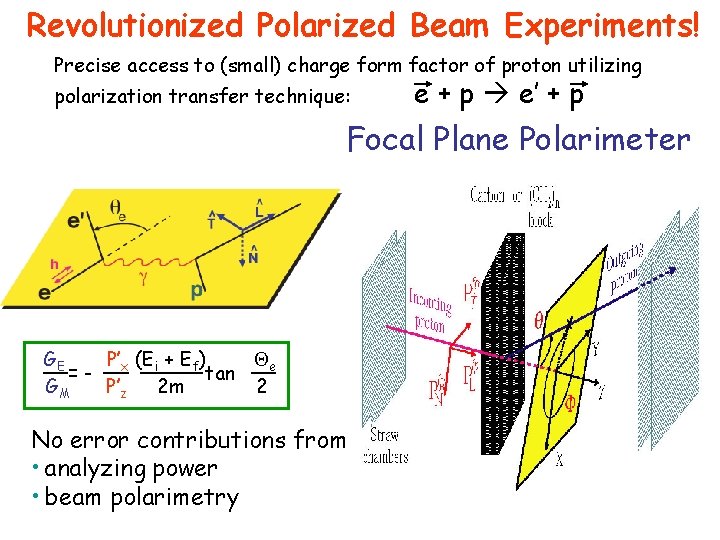
Revolutionized Polarized Beam Experiments! Precise access to (small) charge form factor of proton utilizing polarization transfer technique: e + p e’ + p Focal Plane Polarimeter GE P’x (E Qe __ __ _____ __ i + Ef) =tan GM P’z 2 m 2 No error contributions from • analyzing power • beam polarimetry
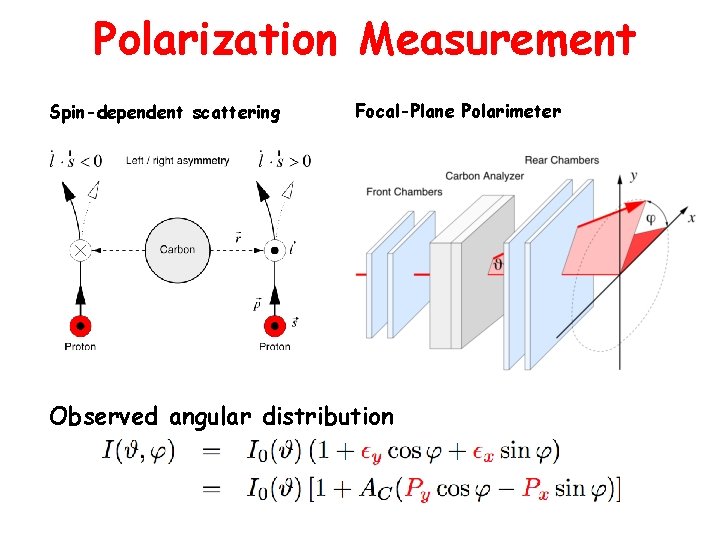
Polarization Measurement Spin-dependent scattering Focal-Plane Polarimeter Observed angular distribution
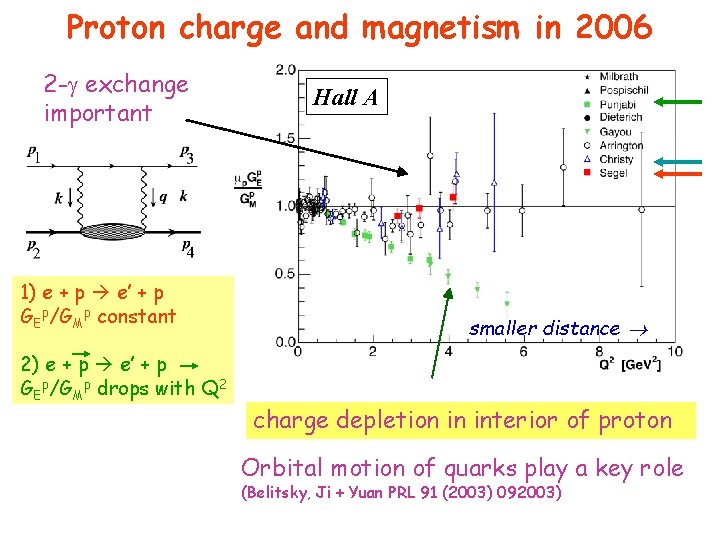
Proton charge and magnetism in 2006 2 - exchange important 1) e + p e’ + p GEp/GMp constant 2) e + p e’ + p GEp/GMp drops with Q 2 Hall A smaller distance charge depletion in interior of proton Orbital motion of quarks play a key role (Belitsky, Ji + Yuan PRL 91 (2003) 092003)
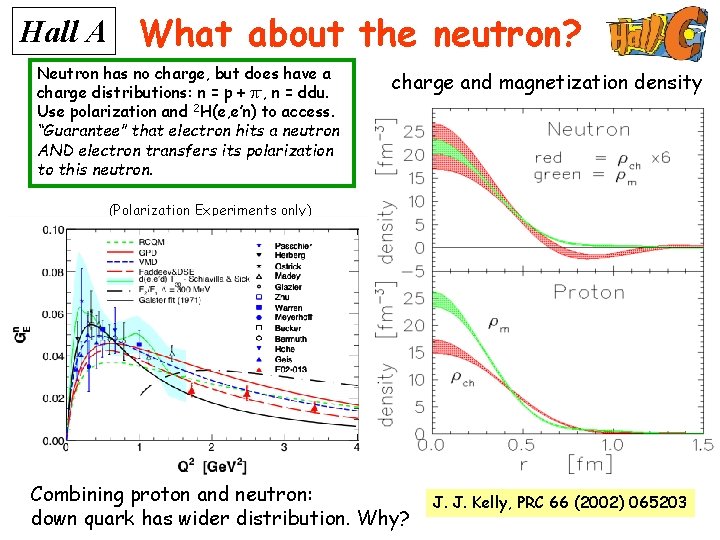
Hall A What about the neutron? Neutron has no charge, but does have a charge distributions: n = p + -, n = ddu. Use polarization and 2 H(e, e’n) to access. “Guarantee” that electron hits a neutron AND electron transfers its polarization to this neutron. charge and magnetization density (Polarization Experiments only) Combining proton and neutron: down quark has wider distribution. Why? J. J. Kelly, PRC 66 (2002) 065203
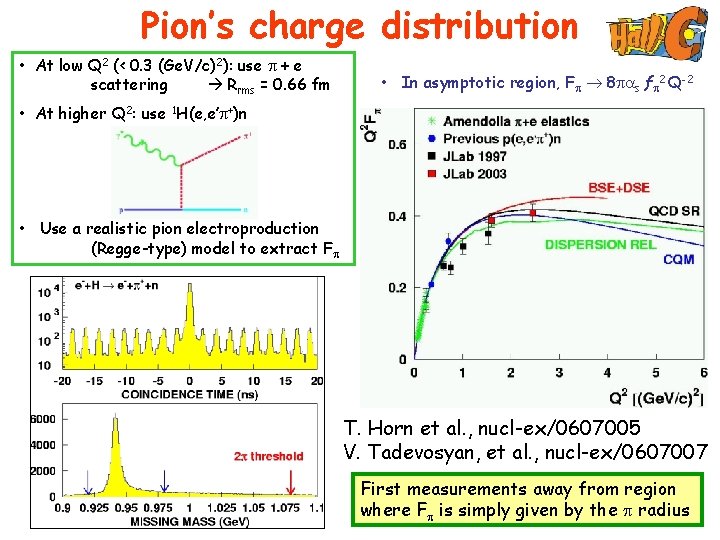
Pion’s charge distribution • At low Q 2 (< 0. 3 (Ge. V/c)2): use + e scattering Rrms = 0. 66 fm • In asymptotic region, F 8 s ƒ 2 Q-2 • At higher Q 2: use 1 H(e, e’ +)n • Use a realistic pion electroproduction (Regge-type) model to extract F T. Horn et al. , nucl-ex/0607005 V. Tadevosyan, et al. , nucl-ex/0607007 First measurements away from region where F is simply given by the radius
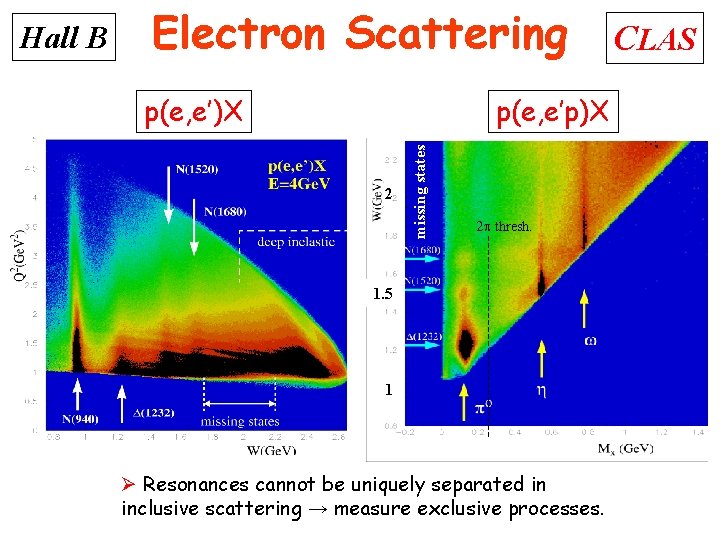
Electron Scattering p(e, e’)X p(e, e’p)X 2 missing states Hall B 2 thresh. 1. 5 1 Ø Resonances cannot be uniquely separated in inclusive scattering → measure exclusive processes. CLAS
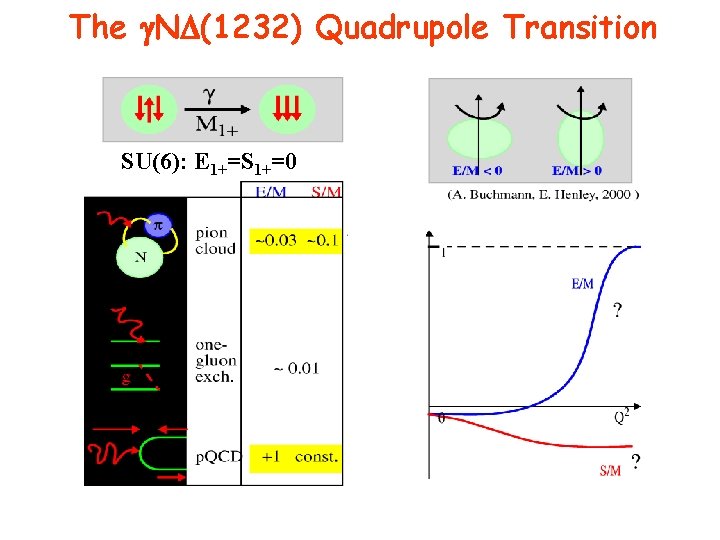
The g. ND(1232) Quadrupole Transition SU(6): E 1+=S 1+=0
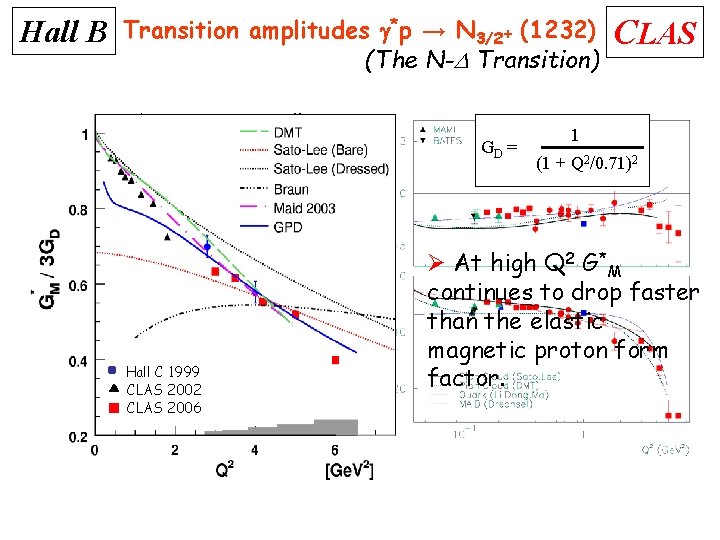
Hall B Transition amplitudes g*p → N 3/2+ (1232) (The N-D Transition) § REM = E 1+/M 1+ remains small and negative at – 2% to -3% from 0 ≤ Q 2 ≤ 6 Ge. V 2. § No trend towards sign change and towards asymptotic behavior. Helicity conservation requires REM → +100(%). § RSM = S 1+/M 1+ remains negative and continues to increase in Hall C 1999 magnitude. No 2002 trend towards CLAS 2006 asymptotic behavior. Helicity conservation requires RSM → constant. GD = CLAS 1 (1 + Q 2/0. 71)2 Ø At high Q 2 G*M continues to drop faster than the elastic magnetic proton form factor.
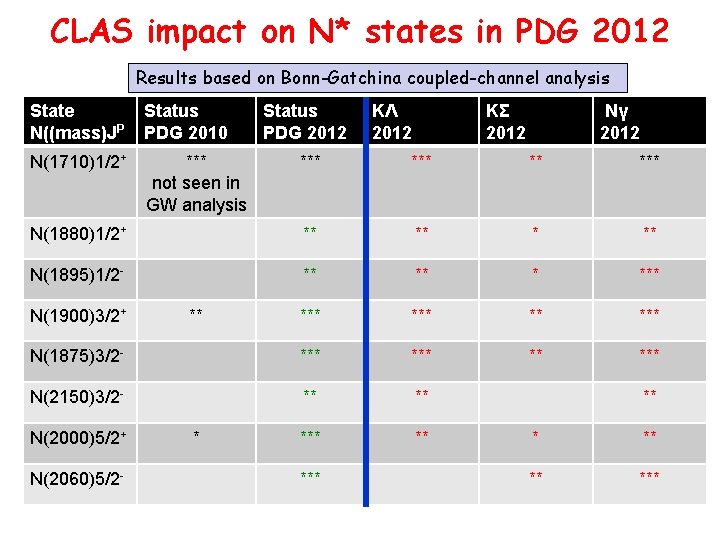
CLAS impact on N* states in PDG 2012 Results based on Bonn-Gatchina coupled-channel analysis State N((mass)JP Status PDG 2010 N(1710)1/2+ *** not seen in GW analysis Status PDG 2012 KΛ 2012 KΣ 2012 Nγ 2012 *** ** *** N(1880)1/2+ ** ** N(1895)1/2 - ** *** ** *** N(1875)3/2 - *** ** *** N(2150)3/2 - ** ** ** N(1900)3/2+ N(2000)5/2+ N(2060)5/2 - ** * ** ** ***

The proton’s magnetic moment Nobel Prize, 1943: "for his contribution to the development of the molecular ray method and his discovery of the magnetic moment of the proton" mp = 2. 5 nuclear magnetons, ± 10% (1933) Otto Stern 2002 experiment: mp = 2. 792847351(28) m. N mn = -1. 91304274(45) m. N 2006 theory: mp ~ 2. 8 m. N mn ~ -1. 8 m. N How do the quark contributions add up? How are charge and magnetism distributed?
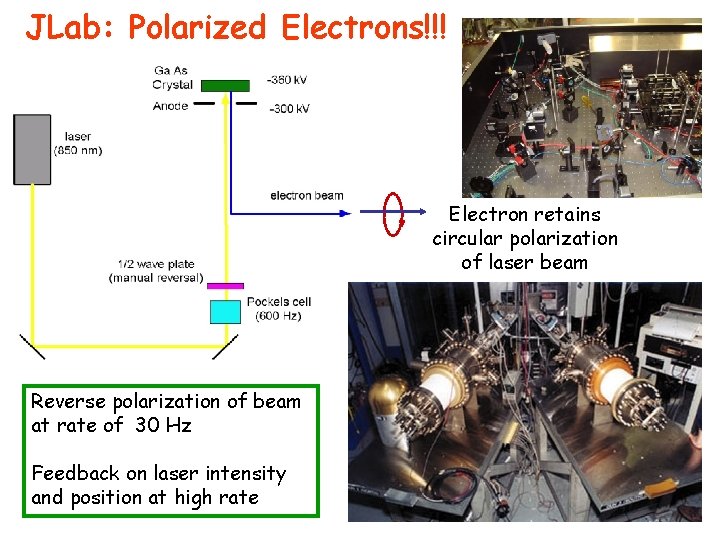
JLab: Polarized Electrons!!! Electron retains circular polarization of laser beam Reverse polarization of beam at rate of 30 Hz Feedback on laser intensity and position at high rate
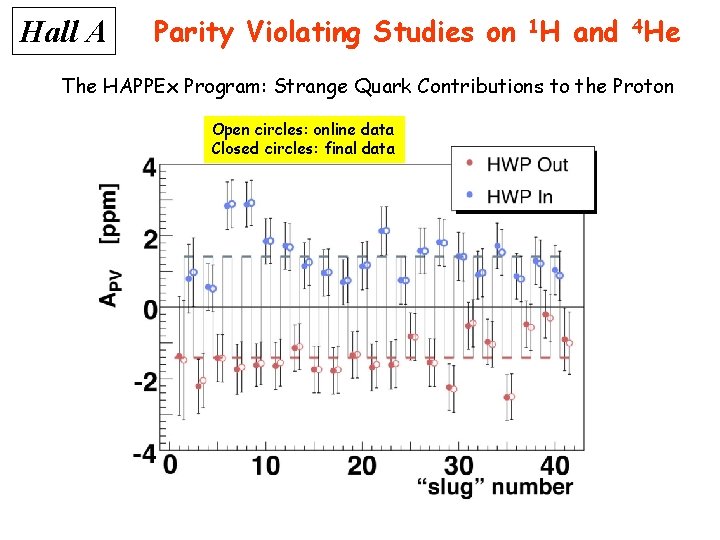
Hall A Parity Violating Studies on 1 H and 4 He The HAPPEx Program: Strange Quark Contributions to the Proton Open circles: online data Closed circles: final data
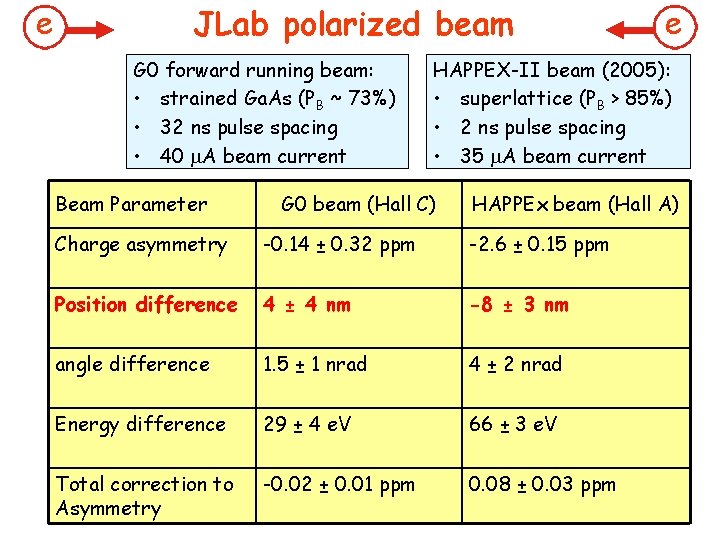
e JLab polarized beam G 0 forward running beam: • strained Ga. As (PB ~ 73%) • 32 ns pulse spacing • 40 m. A beam current Beam Parameter e HAPPEX-II beam (2005): • superlattice (PB > 85%) • 2 ns pulse spacing • 35 m. A beam current G 0 beam (Hall C) HAPPEx beam (Hall A) Charge asymmetry -0. 14 ± 0. 32 ppm -2. 6 ± 0. 15 ppm Position difference 4 ± 4 nm -8 ± 3 nm angle difference 1. 5 ± 1 nrad 4 ± 2 nrad Energy difference 29 ± 4 e. V 66 ± 3 e. V Total correction to Asymmetry -0. 02 ± 0. 01 ppm 0. 08 ± 0. 03 ppm

The Structure of the Proton Naïve Quark Model: proton = uud (valence quarks) QCD: proton = uud + uu + dd + ss + … The proton sea has a non-trivial structure: u ≠ d How much do virtual strange quark-antiquark pairs contribute to the structure of the proton? proton charge/magnetism neutron charge/magnetism proton response to Weak force Hall A up down strange
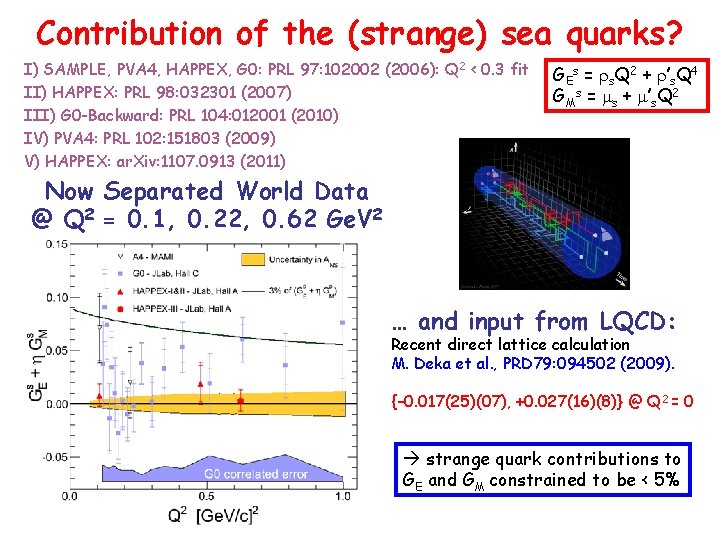
Contribution of the (strange) sea quarks? I) SAMPLE, PVA 4, HAPPEX, G 0: PRL 97: 102002 (2006): Q 2 < 0. 3 fit II) HAPPEX: PRL 98: 032301 (2007) III) G 0 -Backward: PRL 104: 012001 (2010) IV) PVA 4: PRL 102: 151803 (2009) V) HAPPEX: ar. Xiv: 1107. 0913 (2011) } GEs = rs. Q 2 + r’s. Q 4 GMs = ms + m’s. Q 2 Now Separated World Data @ Q 2 = 0. 1, 0. 22, 0. 62 Ge. V 2 … and input from LQCD: Recent direct lattice calculation M. Deka et al. , PRD 79: 094502 (2009). {– 0. 017(25)(07), +0. 027(16)(8)} @ Q 2 = 0 strange quark contributions to GE and GM constrained to be < 5%

CEBAF’s Original Mission Statement Key Mission and Principal Focus (1987): The study of the largely unexplored transition between the nucleon-meson and the quark-gluon descriptions of nuclear matter. The Role of Quarks in Nuclear Physics Related Areas of Study: • Do individual nucleons change their size, shape, and quark structure in the nuclear medium? • How do nucleons cluster in the nuclear medium? • What are the properties of the force which binds quarks into nucleons and nuclei at distances where this force is strong and the quark confinement mechanism is important? Pushing the Limits of the Standard Model of Nuclear Physics Charge and Magnetization in Nucleons and Pions The Onset of the Parton Model
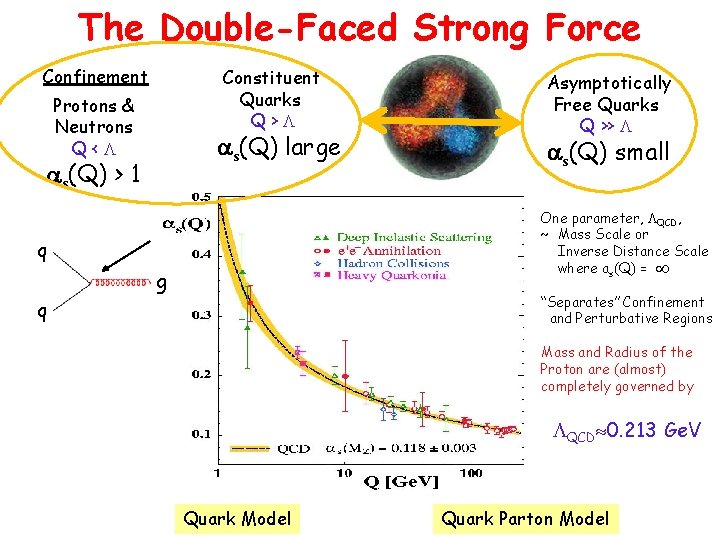
The Double-Faced Strong Force Confinement Protons & Neutrons Q< x as(Q) > 1 Constituent Quarks Q> as(Q) large Asymptotically Free Quarks Q >> as(Q) small One parameter, QCD, ~ Mass Scale or Inverse Distance Scale where as(Q) = q g “Separates” Confinement and Perturbative Regions q Mass and Radius of the Proton are (almost) completely governed by QCD 0. 213 Ge. V Quark Model Quark Parton Model

Nuclear Physics in terms of protons, neutrons and pion exchange is a very good effective model. Momentum transfer Q is negligible Protons and Neutrons in terms of constituent (valence) quarks is a very decent effective model: the Constituent Quark Model works surprisingly well. Momentum transfer Q is small Looking deep inside protons and neutrons, they are really balls of energy, with lots of gluons and quark-antiquark pairs popping in and out of existence. Momentum transfer Q is “large”
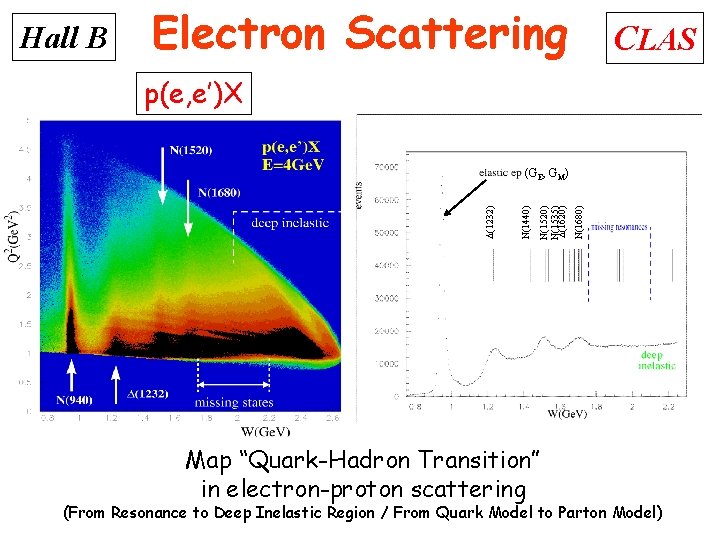
Hall B Electron Scattering CLAS p(e, e’)X Map “Quark-Hadron Transition” in electron-proton scattering N(1680) N(1520) N(1535) (1620) N(1440) (1232) (GE, GM) (From Resonance to Deep Inelastic Region / From Quark Model to Parton Model)
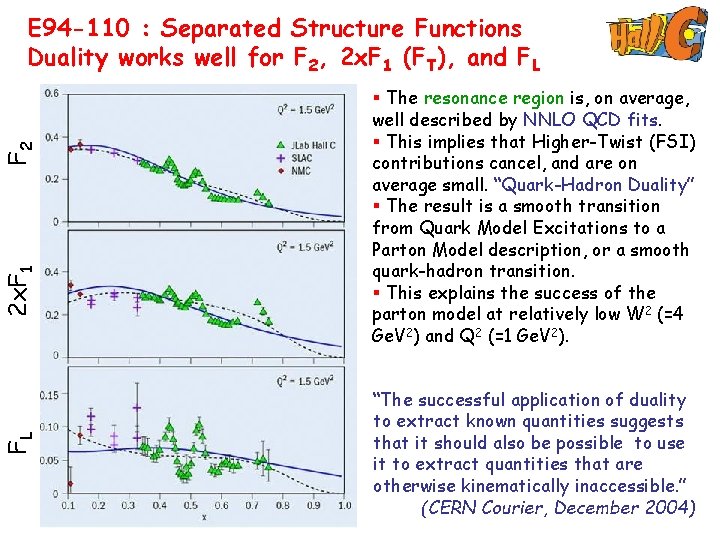
FL 2 x. F 1 F 2 E 94 -110 : Separated Structure Functions Duality works well for F 2, 2 x. F 1 (FT), and FL § The resonance region is, on average, well described by NNLO QCD fits. § This implies that Higher-Twist (FSI) contributions cancel, and are on average small. “Quark-Hadron Duality” § The result is a smooth transition from Quark Model Excitations to a Parton Model description, or a smooth quark-hadron transition. § This explains the success of the parton model at relatively low W 2 (=4 Ge. V 2) and Q 2 (=1 Ge. V 2). “The successful application of duality to extract known quantities suggests that it should also be possible to use it to extract quantities that are otherwise kinematically inaccessible. ” (CERN Courier, December 2004)
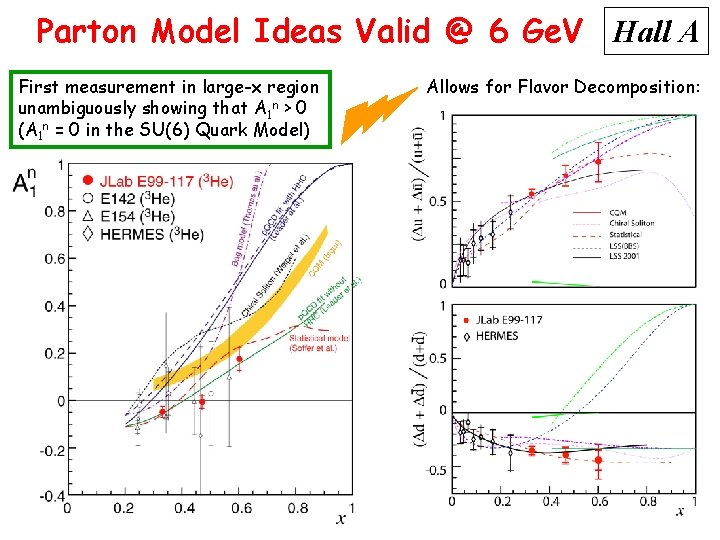
Parton Model Ideas Valid @ 6 Ge. V Hall A First measurement in large-x region unambiguously showing that A 1 n > 0 (A 1 n = 0 in the SU(6) Quark Model) Allows for Flavor Decomposition: A 1 n in Parton Model ~ x = fraction of nucleon momentum carried by struck quark
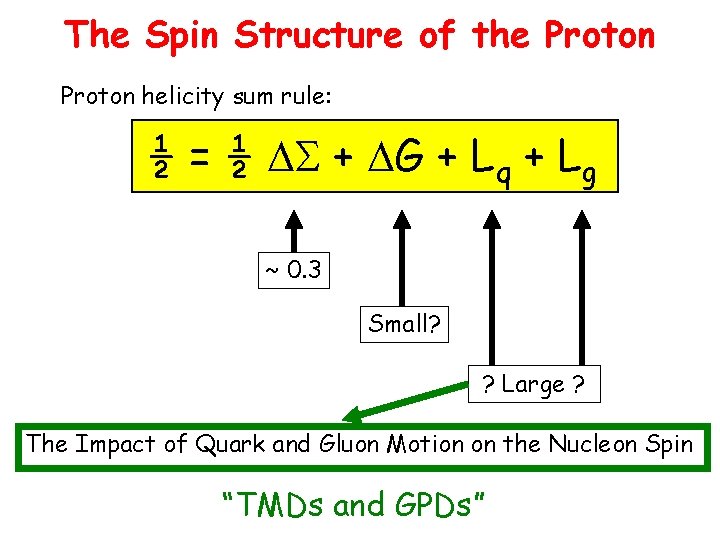
The Spin Structure of the Proton helicity sum rule: ½ = ½ S + G + Lq + Lg ~ 0. 3 Small? ? Large ? The Impact of Quark and Gluon Motion on the Nucleon Spin “TMDs and GPDs”
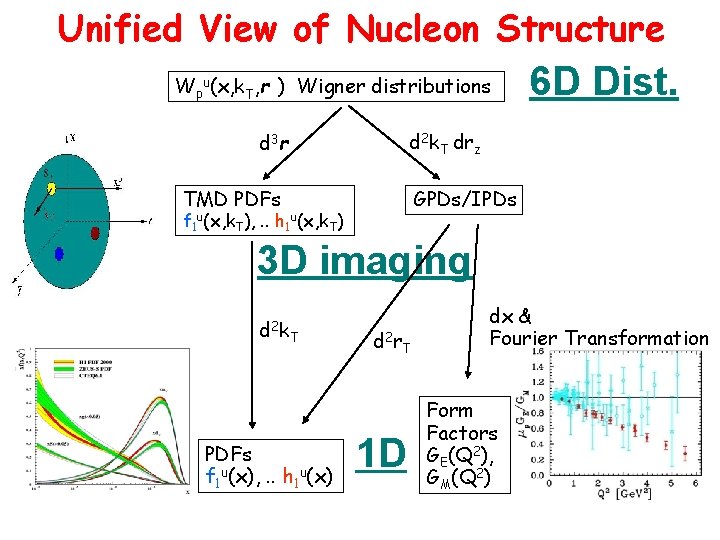
Unified View of Nucleon Structure Wpu(x, k. T, r ) Wigner distributions 6 D Dist. d 2 k. T drz d 3 r TMD PDFs GPDs/IPDs f 1 u(x, k. T), . . h 1 u(x, k. T) 3 D imaging d 2 k T PDFs f 1 u(x), . . h 1 u(x) d 2 r. T 1 D dx & Fourier Transformation Form Factors GE(Q 2), GM(Q 2)
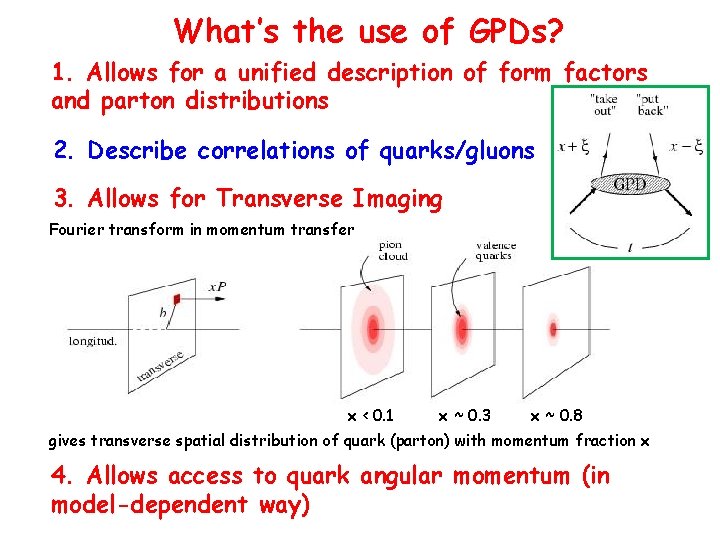
What’s the use of GPDs? 1. Allows for a unified description of form factors and parton distributions 2. Describe correlations of quarks/gluons 3. Allows for Transverse Imaging Fourier transform in momentum transfer x < 0. 1 x ~ 0. 3 x ~ 0. 8 gives transverse spatial distribution of quark (parton) with momentum fraction x 4. Allows access to quark angular momentum (in model-dependent way)
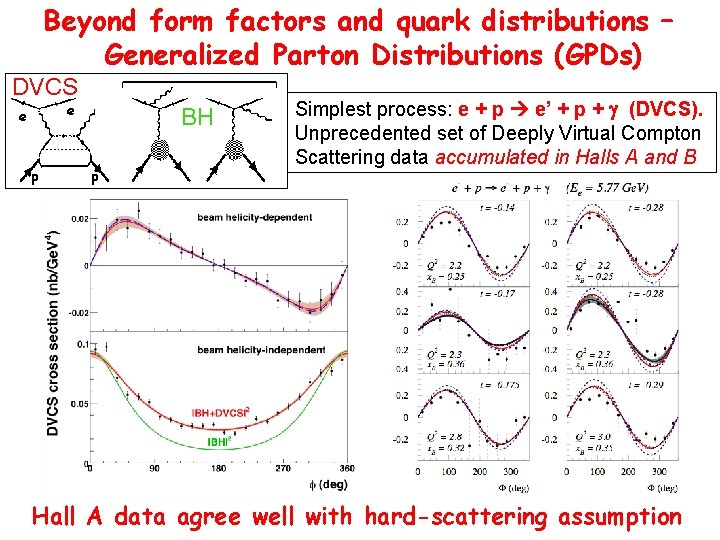
Beyond form factors and quark distributions – Generalized Parton Distributions (GPDs) DVCS e e p BH p Simplest process: e + p e’ + p + g (DVCS). Unprecedented set of Deeply Virtual Compton Scattering data accumulated in Halls A and B Hall A data agree well with hard-scattering assumption
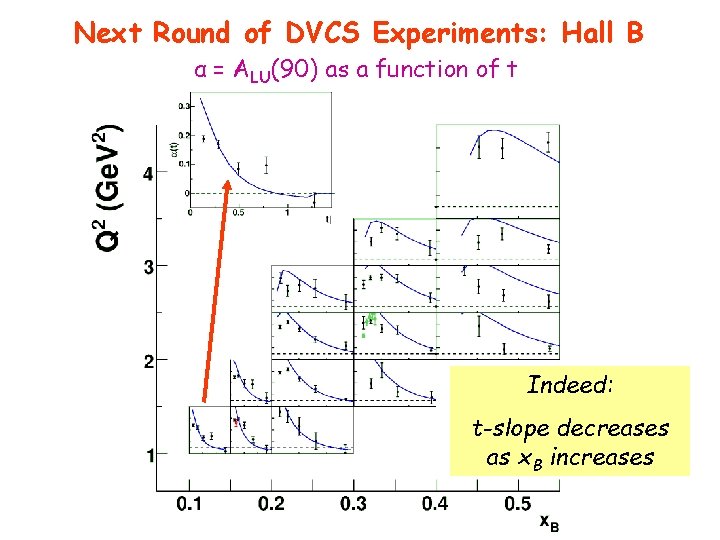
Next Round of DVCS Experiments: Hall B α = ALU(90) as a function of t Indeed: t-slope decreases as x. B increases
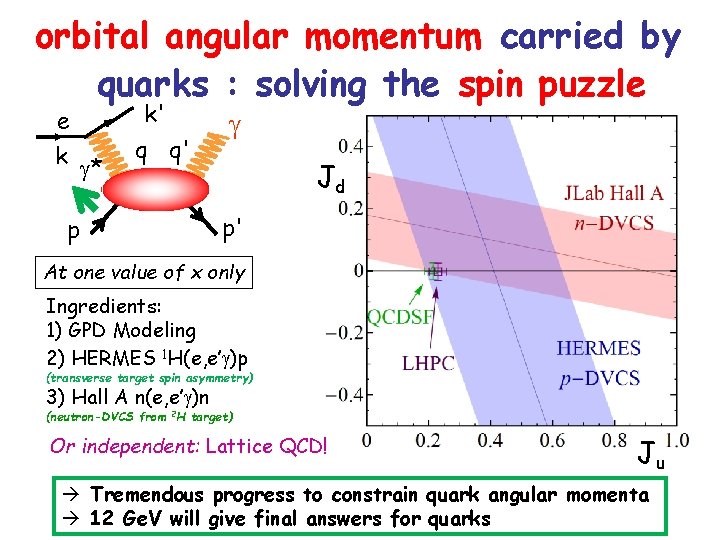
orbital angular momentum carried by quarks : solving the spin puzzle e k k' * q q' p Jd p' At one value of x only Ingredients: 1) GPD Modeling 2) HERMES 1 H(e, e’ )p (transverse target spin asymmetry) 3) Hall A n(e, e’ )n (neutron-DVCS from 2 H target) Or independent: Lattice QCD! Ju Tremendous progress to constrain quark angular momenta 12 Ge. V will give final answers for quarks
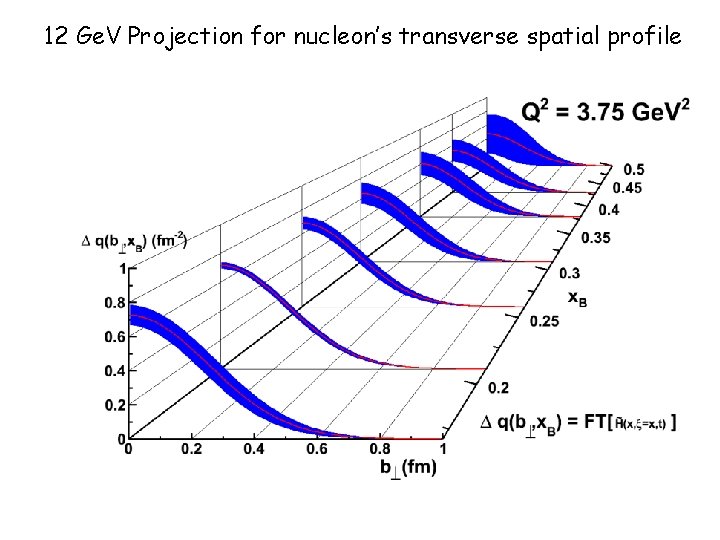
12 Ge. V Projection for nucleon’s transverse spatial profile
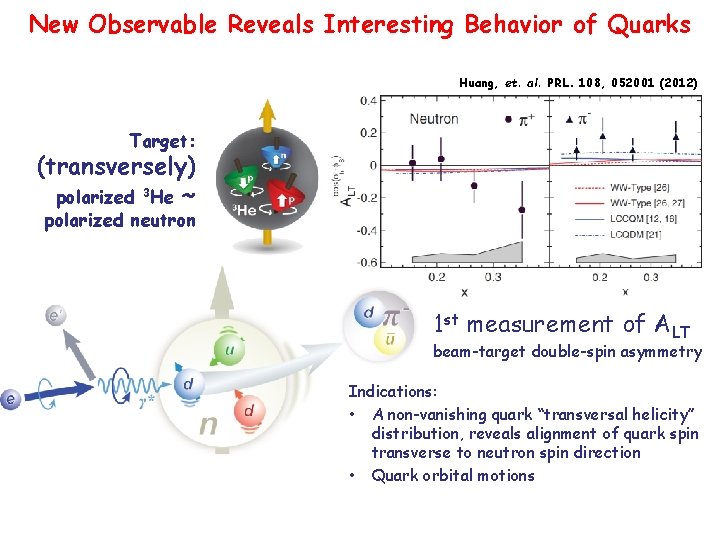
New Observable Reveals Interesting Behavior of Quarks Huang, et. al. PRL. 108, 052001 (2012) Target: (transversely) polarized 3 He ~ polarized neutron 1 st measurement of ALT beam-target double-spin asymmetry Indications: • A non-vanishing quark “transversal helicity” distribution, reveals alignment of quark spin transverse to neutron spin direction • Quark orbital motions
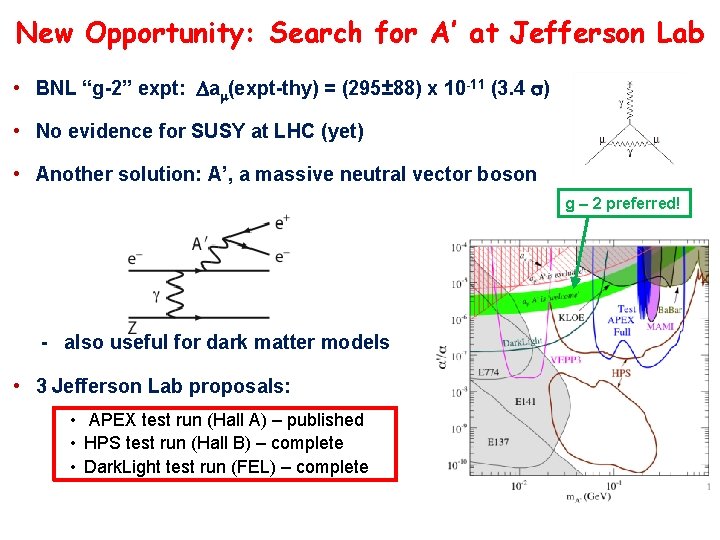
New Opportunity: Search for A’ at Jefferson Lab • BNL “g-2” expt: Dam(expt-thy) = (295± 88) x 10 -11 (3. 4 s) • No evidence for SUSY at LHC (yet) • Another solution: A’, a massive neutral vector boson g – 2 preferred! - also useful for dark matter models • 3 Jefferson Lab proposals: • APEX test run (Hall A) – published • HPS test run (Hall B) – complete • Dark. Light test run (FEL) – complete

15+ Years of Physics Experiments at JLab • Experiments have successfully adressed original Mission Statement: “The study of the largely unexplored transition between the nucleon-meson and the quark-gluon descriptions of nuclear matter” Highlight 1: The Role of Quarks in Nuclear Physics Probing the Limits of the Traditional Model of Nuclei • Emphasis has shifted to third sub-area of intended CEBAF research: “What are the properties of the force which binds quarks into nucleons and nuclei at distances where this force is strong and the quark confinement mechanism is important? ” • Highlight 2: Charge and Magnetization in Nucleons and Pions Charge distribution in proton differs from magnetization distribution Elusive charge distribution of neutron well mapped out to high resolution Strange quarks play <5% role in mass of proton. • Highlight 3: The Onset of the Parton Model at Low Energies High quality hadronic structure function data at JLab at 6 Ge. V have been accumulated spanning the nucleon resonance and low-W 2 deep inelastic region. The data indicate a surprisingly smooth parton-hadron transition at relatively low Q 2, allowing, for x > 0. 1, an unprecedented access to partons with the 12 Ge. V Upgrade, allowing to finally go beyond 1 -dimensional snapshots.

2 H(e, e)2 H elastic scattering 2 H: spin-1 3 form factors to disentangle Solution: measure tensor polarization in 2 H(e, e’d) “T 20 experiment” used HMS to detect the scattered electrons and a dedicated magnetic spectrometer on the 1 st large installation experiment: 1997 floor to detect the recoiling deuteron and measure it’s tensor polarization
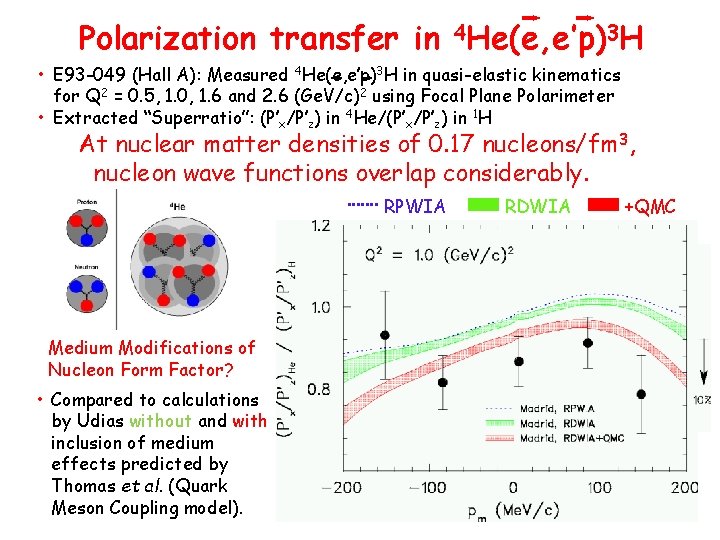
Polarization transfer in 4 He(e, e’p)3 H • E 93 -049 (Hall A): Measured 4 He(e, e’p)3 H in quasi-elastic kinematics for Q 2 = 0. 5, 1. 0, 1. 6 and 2. 6 (Ge. V/c)2 using Focal Plane Polarimeter • Extracted “Superratio”: (P’x/P’z) in 4 He/(P’x/P’z) in 1 H At nuclear matter densities of 0. 17 nucleons/fm 3, nucleon wave functions overlap considerably. RPWIA Medium Modifications of Nucleon Form Factor? • Compared to calculations by Udias without and with inclusion of medium effects predicted by Thomas et al. (Quark Meson Coupling model). RDWIA +QMC
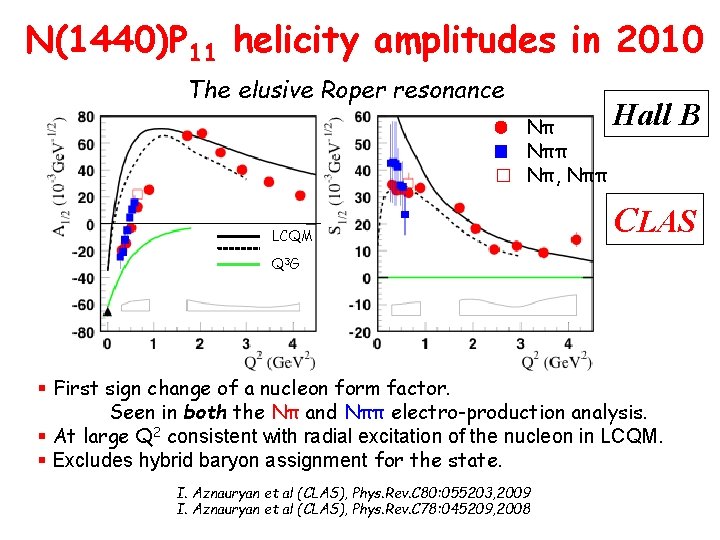
N(1440)P 11 helicity amplitudes in 2010 The elusive Roper resonance Nπ Nπ, Nππ LCQM Hall B CLAS Q 3 G § First sign change of a nucleon form factor. Seen in both the Nπ and Nππ electro-production analysis. § At large Q 2 consistent with radial excitation of the nucleon in LCQM. § Excludes hybrid baryon assignment for the state. I. Aznauryan et al (CLAS), Phys. Rev. C 80: 055203, 2009 I. Aznauryan et al (CLAS), Phys. Rev. C 78: 045209, 2008
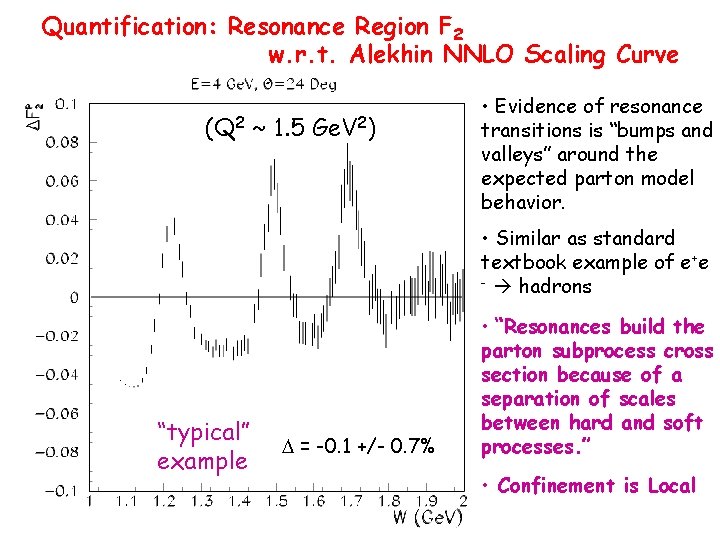
Quantification: Resonance Region F 2 w. r. t. Alekhin NNLO Scaling Curve (Q 2 ~ 1. 5 Ge. V 2) • Evidence of resonance transitions is “bumps and valleys” around the expected parton model behavior. • Similar as standard textbook example of e+e - hadrons “typical” example = -0. 1 +/- 0. 7% • “Resonances build the parton subprocess cross section because of a separation of scales between hard and soft processes. ” • Confinement is Local
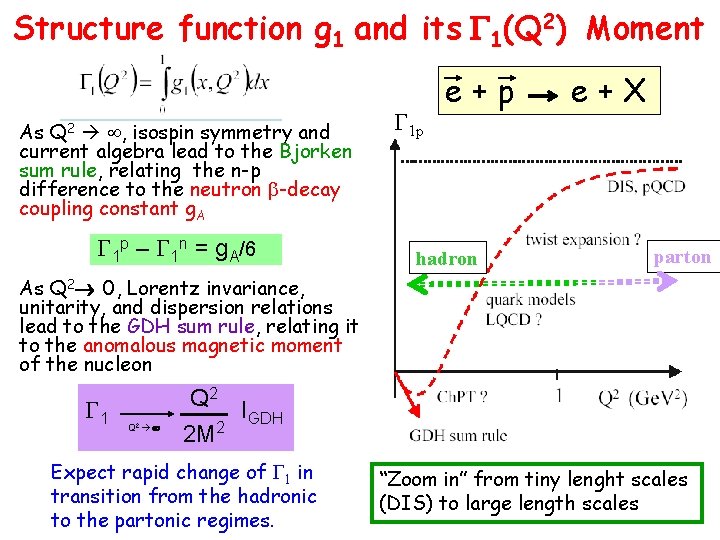
Structure function g 1 and its G 1(Q 2) Moment As Q 2 , isospin symmetry and current algebra lead to the Bjorken sum rule, relating the n-p difference to the neutron b-decay coupling constant g. A G 1 p – G 1 n = g. A/6 G 1 p e+p hadron e+X parton As Q 2 0, Lorentz invariance, unitarity, and dispersion relations lead to the GDH sum rule, relating it to the anomalous magnetic moment of the nucleon G 1 Q 2 I GDH 2 2 M Expect rapid change of G 1 in transition from the hadronic to the partonic regimes. “Zoom in” from tiny lenght scales (DIS) to large length scales
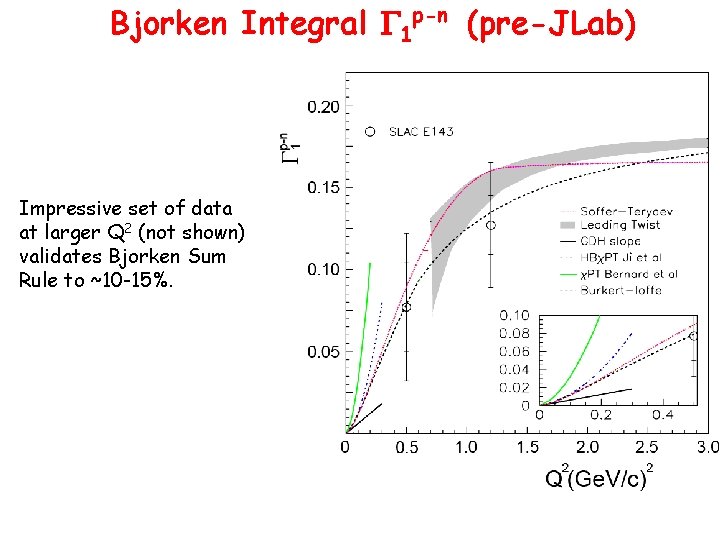
Bjorken Integral G 1 p-n (pre-JLab) Impressive set of data at larger Q 2 (not shown) validates Bjorken Sum Rule to ~10 -15%.
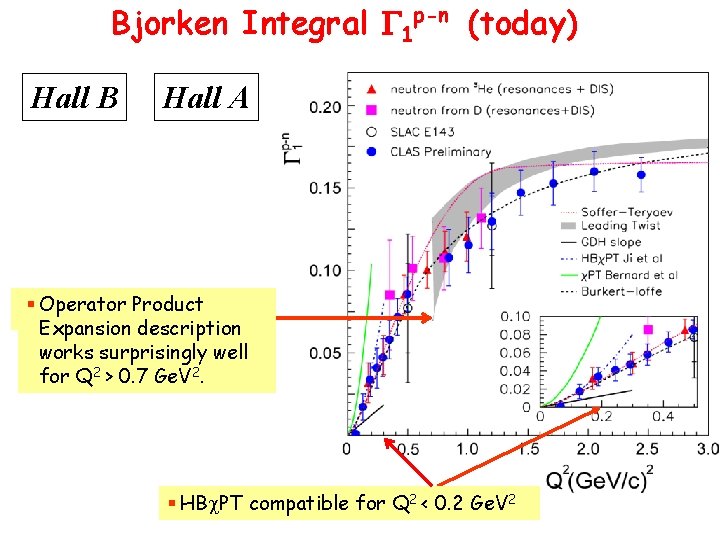
Bjorken Integral G 1 p-n (today) Hall B Hall A § Operator Product Expansion description works surprisingly well for Q 2 > 0. 7 Ge. V 2. § HBc. PT compatible for Q 2 < 0. 2 Ge. V 2
- Slides: 74