Overview of Digital Signal Processing Unit I and

Overview of Digital Signal Processing: (Unit I and II) Prof. H. D. Sonawane, Computer Department, BVCOE&RI, Nashik 1

Contents. . . Signals, Classifications Standard Signals in DSP: u(n) and δ(n) Convolution form Signal operations DT systems, properties Impulse and Step Response Representation of DT system: Modelling Impulse Response and Difference Equation FIR and IIR System DSP system, Sampling process, DT frequencies Aliasing Use of Transducers in signal processing 2

Contd. . . Fourier Series and Fourier Transform (DTFT) Properties of DTFT FT and DFT Significance of N, DFT Spectrum Twiddle factors DFT Properties Circular Convolution CC and LC, Linear Filtering CC using DFT and IDFT Spectral Leakage Analysis frequencies FFT Algorithms 3

Contd. . . Z- Transform (ZT) Significance of ROC ZT and DTFT, DFT Rational ZT, Pole Zero Plot System function H(Z) Difference Equation, Pole Zero Plot and H(Z) Analysis of DT LTI Systems Frequency Response DT System as Filters FIR and IIR Filters Design of Filters Filter Structures 4

DT Signals and Systems Signal : A physical quantity containing some useful information and function of one or more than one independent variable e. g. speech, image, video, ECG, EEG, seismic, radio etc. Signal processing concerned with mathematical representations of signals and algorithmic operations to extract useful information from the signals Signal domains : spatial (signal uses distance as an independent parameter i. e. time) and transformed domain like Frequency or Z-domain DT System – signal processing device 5

DT signals are the forms of CT signals obtained from the process of sampling Sampling forms a bridge between CT and DT domain Representations: 1. Sequence Representation 2. Graphical Representation 3. Mathematical Form 4. Tabular Representation 6

Classifications of signals 1. 2. 3. 4. 5. 1 -D, 2 -D, 3 -D signals Even and Odd signals Periodic and Aperiodic signals Causal and Noncausal signals Deterministic and Nondeterministic signals 7

Standard Signals Unit step signal: u(n) Unit impulse signal /Unit sample sequence : δ(n) e. g. Any arbitrary DT sequence can be represented by means of δ(n) (weighted, shifted version of δ(n) ) x(n) = {1, -2, 3, 2, -1} = δ(n) – 2. δ(n-1) + 3. δ(n-2)+ 2. δ(n-3) - δ(n-4) 8

Thus, = x(n) * δ(n) Likewise, u(n) = u(n) * δ(n) Convolution form Also, δ(n) = u(n) – u(n-1) Computational complexity of a linear convolution : with x(n) and h(n) having N samples Total multiplications = N. (2 N – 1) Total additions = (N-1). (2 N – 1) 9

Operations performed on DT signals 1. Reflection (Folding/Time Reversal) : x(-n) 2. Time Shifting: Advancing : x(n + k) Delaying: x(n - k) 3. Time Scaling: Expansion: x(n/k) Compression: x(n. k) k: scaling factor 4. Inversion (Amplitude Scaling): - x(n) i. e. A. x(n) where A= -1 5. Additions, Subtractions, Multiplications etc. 10

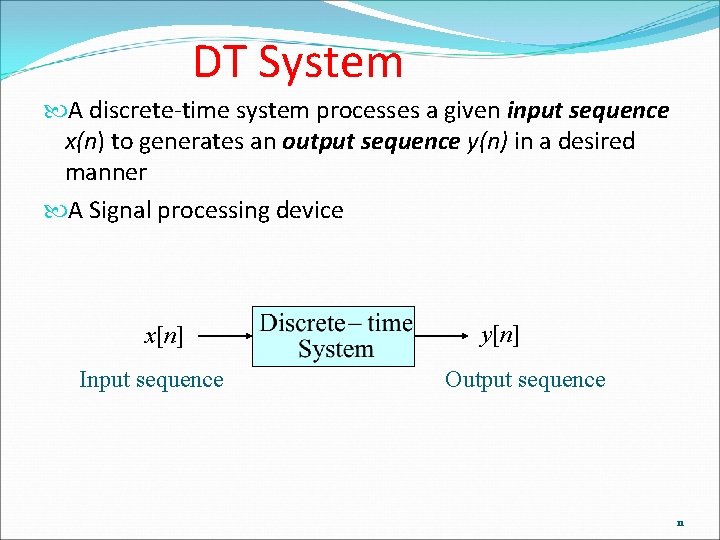
DT System A discrete-time system processes a given input sequence x(n) to generates an output sequence y(n) in a desired manner A Signal processing device x[n] Input sequence y[n] Output sequence 11

Properties of DT System Dynamicity: 1) static 2) dynamic Causality: 1) causal 2) non-causal Time Invariance (TIV) Stability Linearity Invertibility 12

Representation Of DT System Impulse Response: h(n) Linear Convolution: y(n) = x(n) * h(n) Difference equation: System Function: H(ω), H(Z) Pole Zero Plot : H(Z) FIR and IIR systems Design of a DT system: h(n) or H(Z) 13

Impulse and Step Responses The response of a discrete-time LTI system to a unit sample sequence δ(n) is called the unit sample response or, simply, the impulse response, and is denoted by h(n) The response of a discrete-time LTI system to a unit step sequence u(n) is called the unit step response or, simply, the step response, and is denoted by s(n) Input x(n) and output y(n) arbitrary; h(n), s(n) : unique which defines the system 14

• Impulse Response LTI • Step Response LTI 15

Impulse Response h(n) and DT System For a static system, h(n) = 0 for n ≠ 0 For a causal system, h(n) = 0 for n < 0 For a stable system, Invertibility where, h 1 (n) : Inverse system Step Response: 16

Impulse Response Example - The impulse response of the system is obtained by setting x[n] = δ[n] The impulse response is thus a finite-length sequence of length 4 given by 17

For FIR system the impulse response is {bk} coeff of difference equation What about IIR system? e. g. y(n) = x(n) + y(n-1) has impulse response h(n) = δ(n) + h(n-1) = u(n) Recursive system Sim, for, y(n) = x(n) + a. y(n-1) h(n) = Non-recursive system : FIR system Recursive system : IIR system DT Systems can be designed as FIR or IIR systems CT Systems ? Analog FIR filters does not present … 18

A DT LTI system is completely characterized by its impulse response Therefore, knowing the impulse response, one can compute the output of the system for any arbitrary input 19

A discrete-time LTI system is denoted as Any arbitrary input sequence x[n] can be expressed as a linear combination of delayed and advanced unit sample sequences in the form The response of the LTI system to an input will be 20

Hence, the response y[n] to an input will be which can be alternately written as 21

The summation is called the convolution sum of the sequences x[n] and h[n] and represented compactly as y[n] = x[n] * h[n] 22

Recursive implementation of a system: gives, y(n) = x(n) + y(n-1) (1) Non. Recursive system viewed as Recursive: gives, y(n) = x(n) + y(n-1) Both systems are same ? (2) 23

Discrete-Time LTI Systems DT LTI systems is characterized by a linear constantcoefficient difference equation of the form x(n) and y(n) are, respectively, the input and the output of the system and parameters which characterize the system The order of the system is given by max(N, M), which is the order of the difference equation FIR and IIR systems 24

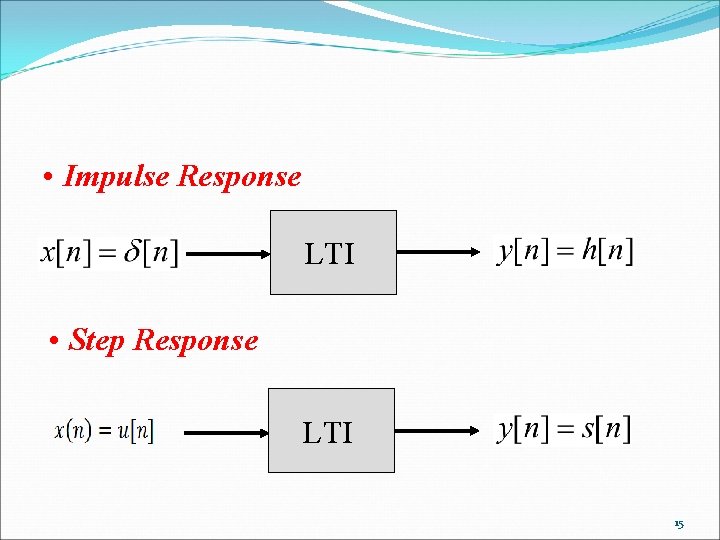
DSP System LPFin ADC DSP DAC LPFout Equivalent Analog Signal Processor ASP 25

ADC 1. Sampler: Conversion of CT signal into continuous amplitude DT signal 2. Quantizer: Conversion of continuous amplitude DT signal into discrete amplitude DT signal. Results into Q error 3. Coder: Represent each DT sample by b-bit binary sequence b ≥ log 2 L L: Quantization levels 26

Analog and DT frequencies CT signal: x(t) = A. cos(2 п. Ft + θ) ------(1) DT signal: x(n) = x(t) | t=n. T=n/Fs = A. cos(2 п. F. n/Fs + θ) ------(2) Also, x(n) = A. cos(2 пfn + θ) ------(3) Thus, f = F/Fs ------(4) And x(n) = A. cos(ωn + θ) ------(5) ω = 2 пf = 2 п. F/Fs = Ω. T -----(6) F: Analog frequency (cycles/s) f: DT frequency (cycles/samples) Fs: Sampling frequency (Samples/s) N = 1/f Period DT signal (samples/cycle) 27

_ Aliasing: Identical sampling Mapping of ∞ analog frequency range onto finite DT frequency range: -1/2 <= f <= +1/2 - п <= ω <= + п Higher frequencies taking form of lower frequencies DT sinusoids having frequencies integer multiple of 2 п are always identical All frequencies are the aliases of frequency F 0 Sampling Theorem Time domain and frequency domain aliasing 28

Transducers and Signal Processing The information presented by the signal may be in the form of a physical phenomenon or may be an electrical signal. The function of the detector (Transducer stage) is to sense the information and convert it into a convenient form for the acceptance. The process of detection and conversion of input signal or information from one form to another requires Energy. If energy is extracted from the signal, it will not be faithfully reproduced after conversion which may leads to errors. So energy should not be distorted and we should get corresponding output without any loss or error. 29

Transducer is a device which converts energy from one form to another. Transducers convert signals from other physical form to electrical current or voltage waveforms, which then are processed, transmitted as electromagnetic waves, received and converted by another transducer to final form. 30

Fourier Transform (DTFT) and DFT Frequency analysis of signals and systems Fourier: Any signal can be viewed as a linear combination of basic sets of signals (decomposition) and can be represented by means of sinusoids Periodic signals : Fourier series Trigonometric form Complex exponential form Aperiodic Signals: Fourier Transform FT is Periodic and continuous spectrum Periodic CT : FS, Aperiodic CT: FT Periodic DT : DFT, Aperiodic DT: DTFT Magnitude and Phase spectrum 31

Properties Linearity Periodicity Time Shifting Frequency Shifting (Modulation Property) Time Reversal Convolution Multiplication of two sequences (Windowing Theorem) 32

DFT Sampled version of FT Efficiently computed by means of digital computer N point DFT : N frequency samples obtained at discrete set of frequencies – Relationship between FT and DFT 33

DFT spectrum: plot of v/s K : gives magnitude for different k K : defines a set of N discrete frequencies ωk N >= L (L: length of the DT signal) Can we compute different N point DFTs for the same DT signal ? Significance ? IDFT gives periodic extended signal Properties: Periodicity, circular symmetry Circular Convolution N-point CC v/s LC 34

Analysis Frequencies ωk = 2 Пk / N = 2 Пfk =2 ПFk / Fs Also, fk = k / N =Fk / Fs Thus, Fk = k. Fs / N 35

Problem of spectral leakage The analysis frequencies observed – k = 0, 1, … (N-1) e. g. If, Fs = 4 K Samples/s, N = 8 Then Fk = {0, 0. 5, 1. 0, 1. 5, 2. 0, 2. 5, 3. 0, 3. 5} If {Fk} are not the part of a given DT signal x(n), then DFT spectrum is not correct giving leakage of actual frequencies 36

Twiddle factor DFT as linear transformation CC using DFT and IDFT as linear filtering LC using N-point CC For LC, N = (L + M – 1) 37

Fast Fourier Transform (FFT) Efficient computation of DFT Radix r FFT Divide and conquer approach Splitting N-pt DFT into smaller DFTs Effective use of Periodicity and Symmetry property Computation of N/2 butterflies in each stage and log 2 N stages Computational complexity is reduced to – N/2. log 2 N multiplications and N. log 2 N additions 38

DIT FFT Algorithm 39

DIF FFT Algorithm 40

N/2 twiddle factors In-place computation Indexing in bit reversal Computing basic butterflies, pairing in each step : 2**k with k = 0, 1, …, (n-1) where n = log 2 N Computation of IDFT using FFT: Reverse the direction of flow graph Change the sign of phase (twiddle) factors Interchange the inputs and outputs Finally divide each output by N 41