Overview AS Level Maths Year 12 Core mathematics







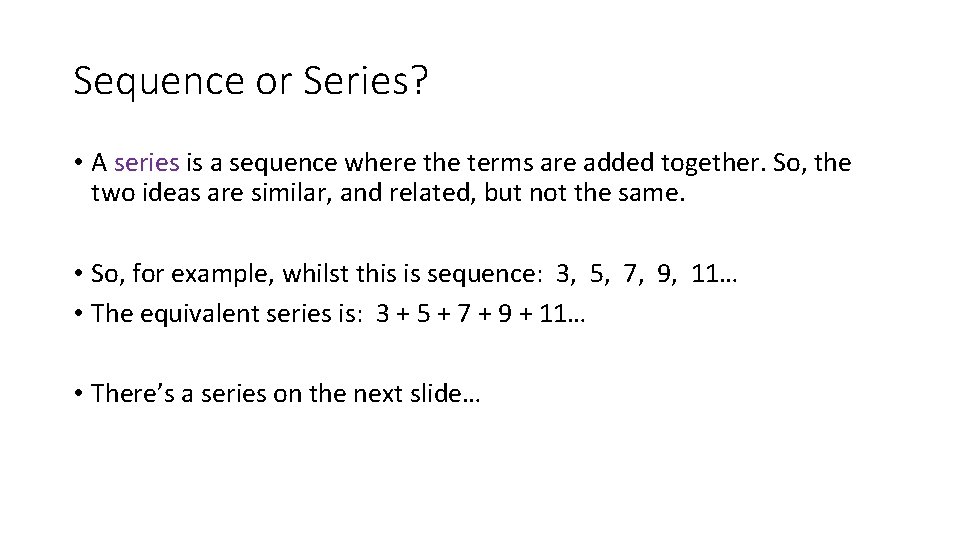

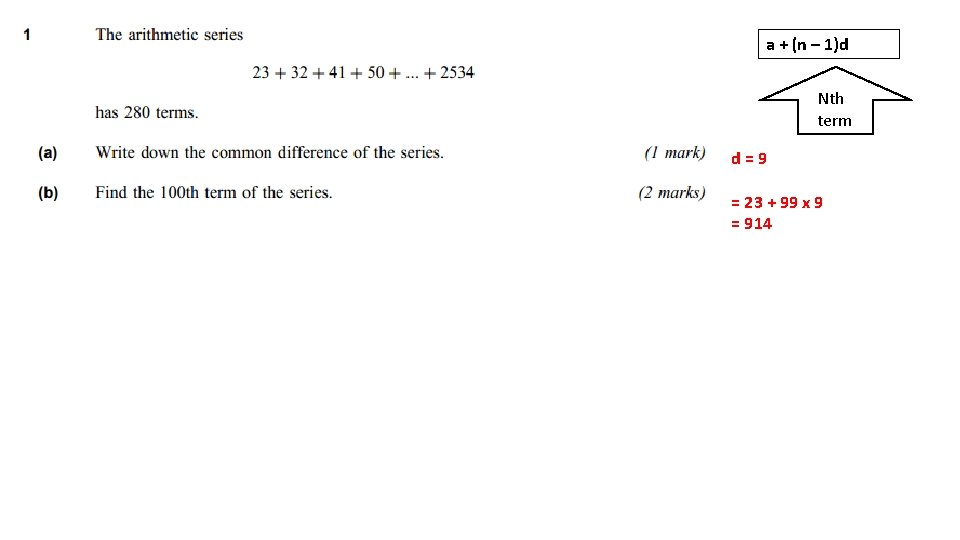
















- Slides: 27

Overview - AS Level Maths – Year 12 • Core mathematics: Proof, Algebra and functions, Coordinate geometry, Sequences and series, Trigonometry, Exponentials and logarithms, Differentiation • Statistics: Statistical sampling, Data presentation and interpretation, Probability, Statistical distributions, Statistical hypothesis testing • Mechanics: Vectors, Quantities and units in mechanics, Kinematics, Forces and Newton’s laws • Two exams in the summer of year 12: • Core and statistics. • Core and mechanics.

Overview - A 2 Level Maths – Year 13 • Core mathematics: Proof, Algebra and functions, Coordinate geometry, Sequences and series, Trigonometry, Exponentials and logarithms, Differentiation, Integration, Numerical methods. • Statistics: Statistical sampling, Data presentation and Interpretation, Probability, Statistical distributions, Statistical hypothesis testing. • Mechanics: Vectors, Quantities and units in mechanics, Kinematics, Forces and Newton’s laws, Moments • Three exams in the summer of year 13: • Core and statistics. • Core and mechanics.

Mr Shaw Gives Some Honest Advice: Only take A Level Maths if: • You like Maths • You’re good at Maths • You’re determined and won’t give up when it gets tough (it’ll get tough for everyone) • You’re prepared to work really hard Don’t do A Level Maths if: • You’re stuck for another subject and can’t think of anything else • You’re pretty sure that all this stuff about working hard is not true, because you never worked hard for GCSE Maths and that worked out okay, so this probably will too. It won’t just work out okay: to do well, you HAVE to put the time and energy in.

It’s best to get one of these before you start: Casio Class. Wiz FX-991 EX (You might be tempted to get a “better”, more expensive model to show serious you are about Maths – you don’t need to, it’s easier if everyone has the same one, because then we’re all learning the same menus).

Time For Actual Maths – Using a Rule for the nth Term Mr Mike the caretaker stacks chairs each of height 80 cm. Two chairs stacked on one another have a combined height of 85 cm. What is the height of 3, 4 and 5 chairs stacked? Create a rule for n chairs. The doors to the storage room are 2 m high, what is the maximum number of chairs Mr Mike can stack?

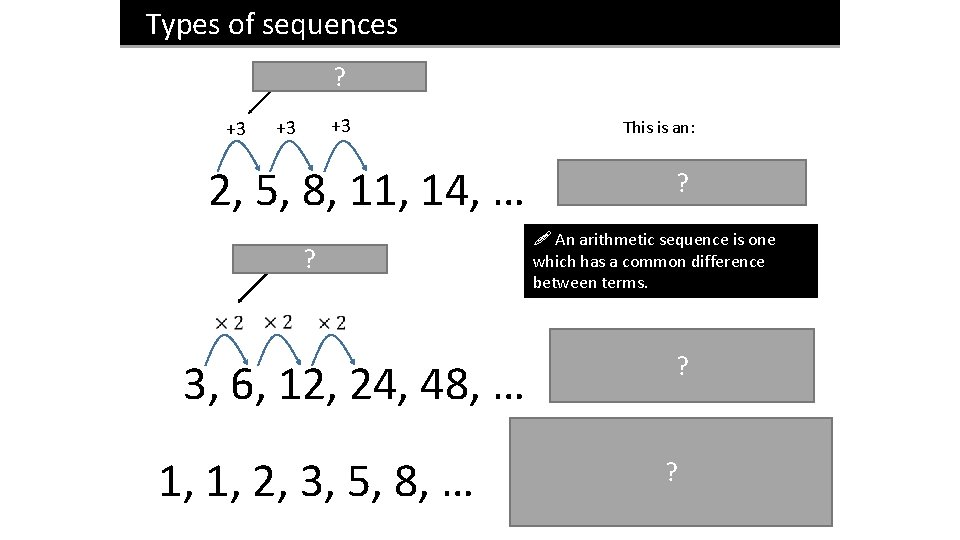
Types of sequences ? +3 +3 +3 This is an: 2, 5, 8, 11, 14, … ! An arithmetic sequence is one which has a common difference between terms. ? ? Arithmetic Sequence 3, 6, 12, 24, 48, … 1, 1, 2, 3, 5, 8, … Geometric Sequence ? (Not today though) This is the Fibonacci Sequence. The terms follow a recurrence relation because each term can be generated using the previous ones. These are studied at other points in the course. ?

So if we look at a typical arithmetic sequence and look for some patterns and properties… 8 11 14 17 20… 8 8 + 1 x 3 8 + 2 x 3 8 + 3 x 3 8 + 4 x 3 We can see that each term of an arithmetic sequence is made up of the starting value, plus some multiple of the common difference. (I’ve tried to do some colour coding here to highlight this)

Arithmetic Sequences An arithmetic sequence is a sequence with an inductive definition in the form u 1=a, un+1 = un + d. i. e. u 1=3, un+1 = un + 4. u 2 = 3 + 4 u 3 = 3 + (……… x 4) u 4 = 3 + (……… x 4) un = 3 + (……… x 4) The 4 th term of an arithmetic sequences is -2 and the 20 th term of the same sequence is 22. What is the nth term of the sequence? u 1 = a u 2 = a + d, The nth term is ……………………… u 4 = a + (……… x d) u 20 = a + (……… x d) How many terms are in the finite arithmetic sequence -10, -7, -4, -1, …………, 137? The nth term is ……………… u 1 = ……… u 2 = ……… + ……… u 3 = ……… + (2 x ………) u 4 = ……… + (……… x ………) un = ……… (What is the last term? ) Can you use this to find a value for n?
Sequence or Series? • A series is a sequence where the terms are added together. So, the two ideas are similar, and related, but not the same. • So, for example, whilst this is sequence: 3, 5, 7, 9, 11… • The equivalent series is: 3 + 5 + 7 + 9 + 11… • There’s a series on the next slide…

a + (n – 1)d Nth term Have a go at this – the answers are on the next slide….
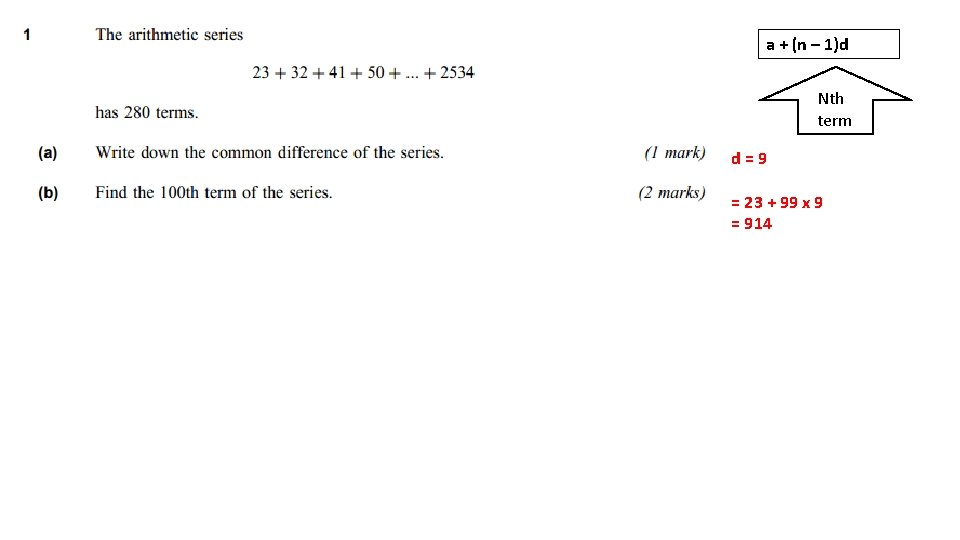
a + (n – 1)d Nth term d=9 = 23 + 99 x 9 = 914

a + (n – 1)d 140 + 19 x 20 = 520 Think about this next one – it’s not been on the Powerpoint yet, so no pressure…but can you figure out a nice quick way to do it?

Arithmetic Series (sum of the terms in an arithmetic sequence) Let’s start with an easier example. . . 1+3+5+7 = 16 I’m also going to write the same in reverse. . . 7+5+3+1 = 16 (or 32 for all 8 numbers) Each pair adds up to 8 so I’ve got 4 lots of 8. I only want the sum of the first four numbers (not all eight) Total amount = 0. 5 x 4(1 + 7)

A Formula for Arithmetic Series Consider a general sequence with first term a and last term l, then the series can be written as…………. a + (a + d) + ………+ (l – d) + l. And the reverse as. l + (l – d) + ………. . + (a +d) + a. 2 x Total amount = (a + l) +. . …. + (a + l) 2 x Total amount = n(a + l) Total amount = 0. 5 n(a + l)

Arithmetic Series – Another, Different, Formula… Example: Proving more generally: ? Let’s prove it! The idea is that each pair of terms, at symmetrically opposite ends, adds to the same number.

Which is best? It depends on what information we have…

Total number of points = 0. 5 n(a + l) 0. 5 x 20(140 + 520) = 6600

Standard Question Challenge Question


a) a + 17 d = 25 a + 20 d = 32. 5 b) a + 20 d = 32. 5 a + 17 d = 25 3 d = 7. 5 d = 2. 5 a + 17(2. 5) = 25 a = -17. 5

Multiply by 2 Divide by 2. 5

Find the sum of the first 30 terms of the following arithmetic sequences… 1 ? 2 ? 3 ? ?

Test Your Understanding Edexcel C 1 Jan 2012 Q 9 ? ?

Sigma Notation What does each bit of this expression mean? The Greek letter, capital sigma, means ‘sum’.

Determining the value First few terms? Final result? ? ? Be careful, there are 11 numbers between 5 and 15 inclusive. Subtract and +1. ? ? ?

Testing Your Understanding Solomon Paper A ? ?

Over the summer • Complete the bridging unit booklet. • You should read through the examples, complete the exercises and mark your own work with the solutions provided at the end. • The content of this will be tested approximately two weeks after you start the course. • If you have any questions about the course, please get in touch with me at: ashaw@nationalce-ac. org. uk