Overfitting occurs when a statistical model describes random

Overfitting occurs when a statistical model describes random error or noise instead of the underlying relationship. Overfitting generally occurs when a model is excessively complex, such as having too many parameters relative to the number of observations. A model which has been overfit will generally have poor predictive performance, as it can exaggerate minor fluctuations in the data.

Suppose we need to solve a classification problem We are not sure if we should us the. . • Simple linear classifier or the • Simple quadratic classifier How do we decide which to use? We do cross validation and choose the best one.

• Simple linear classifier gets 81% accuracy • Simple quadratic classifier 99% accuracy 100 90 80 70 60 50 40 30 20 10 10 20 30 40 50 60 70 80 90 100

• Simple linear classifier gets 96% accuracy • Simple quadratic classifier 97% accuracy

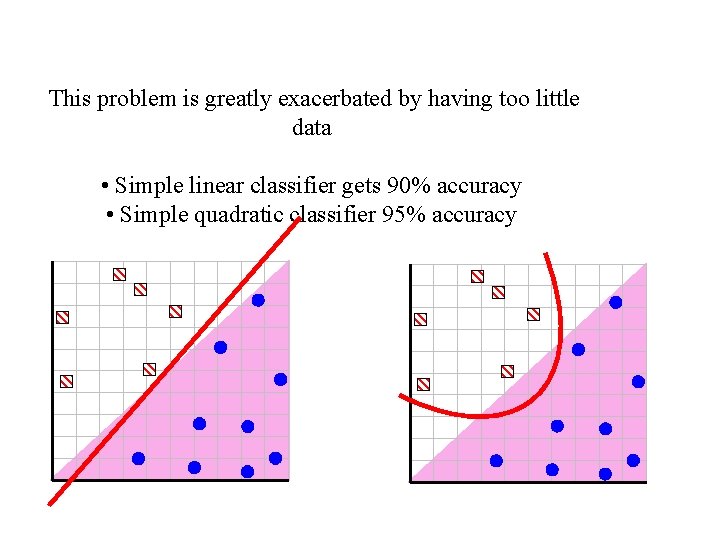
This problem is greatly exacerbated by having too little data • Simple linear classifier gets 90% accuracy • Simple quadratic classifier 95% accuracy

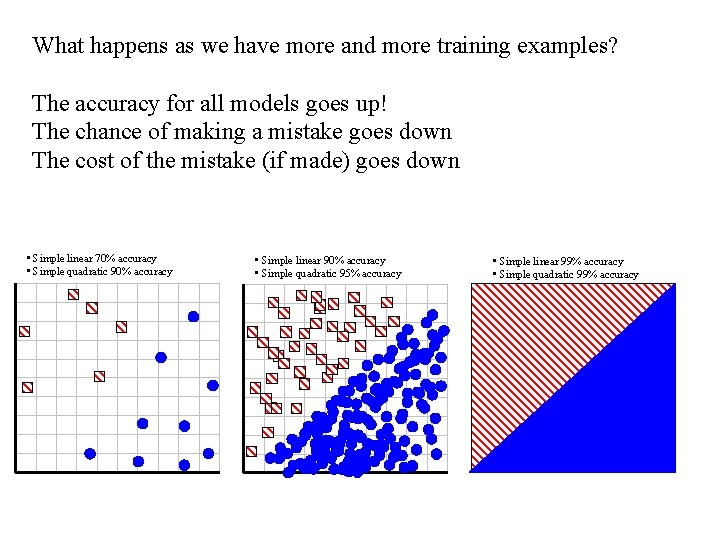
What happens as we have more and more training examples? The accuracy for all models goes up! The chance of making a mistake goes down The cost of the mistake (if made) goes down • Simple linear 70% accuracy • Simple quadratic 90% accuracy • Simple linear 90% accuracy • Simple quadratic 95% accuracy • Simple linear 99% accuracy • Simple quadratic 99% accuracy

One Solution: Charge Penalty for complex models • For example, for the simple {polynomial} classifier, we could charge 1% for every increase in the degree of the polynomial • Simple linear classifier gets 90. 5% • Simple quadratic classifier 97. 0% • Simple cubic classifier 97. 05% Accuracy = 90. 5% 10 9 8 7 6 5 4 3 2 1 accuracy, minus 0, equals 90. 5% accuracy, minus 1, equals 96. 0% accuracy, minus 2, equals 95. 05% Accuracy = 97. 0% 10 9 8 7 6 5 4 3 2 1 1 2 3 4 5 6 7 8 9 10 Accuracy = 97. 05% 10 9 8 7 6 5 4 3 2 1 1 2 3 4 5 6 7 8 9 10

One Solution: Charge Penalty for complex models • For example, for the simple {polynomial} classifier, we could charge 1% for every increase in the degree of the polynomial. • There are more principled ways to charge penalties • In particular, there is a technique called Minimum Description Length (MDL)

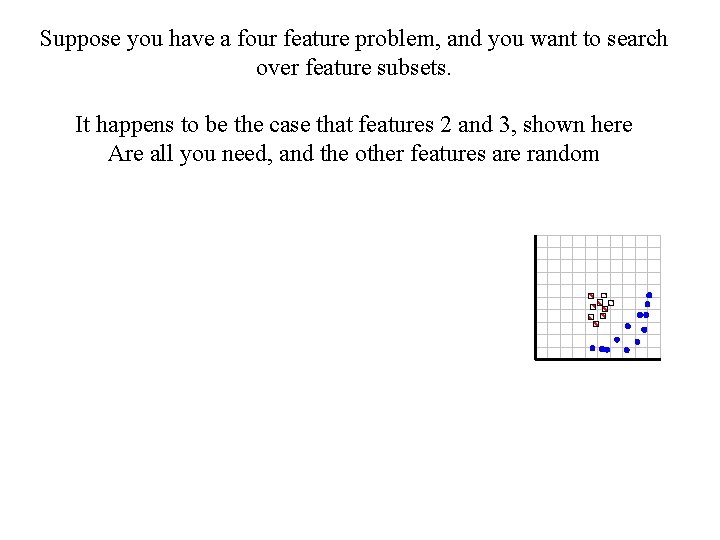
Suppose you have a four feature problem, and you want to search over feature subsets. It happens to be the case that features 2 and 3, shown here Are all you need, and the other features are random

Suppose you have a four feature problem, and you want to search over feature subsets. It happens to be the case that features 2 and 3, shown here all you need, and the other features are random 1, 2, 3 1 2 3 4 1, 3 2, 3 1, 4 2, 4 1, 3, 4 2, 3, 4 1, 2, 3, 4 0 1 2 3 4

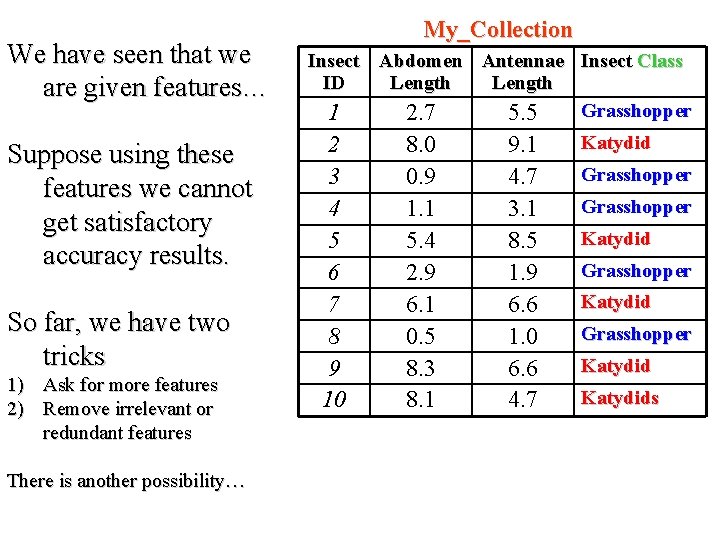
We have seen that we are given features… Suppose using these features we cannot get satisfactory accuracy results. So far, we have two tricks 1) Ask for more features 2) Remove irrelevant or redundant features There is another possibility… My_Collection Insect Abdomen Antennae Insect Class ID Length Grasshopper 1 2. 7 5. 5 2 3 4 5 6 7 8 9 10 8. 0 0. 9 1. 1 5. 4 2. 9 6. 1 0. 5 8. 3 8. 1 9. 1 4. 7 3. 1 8. 5 1. 9 6. 6 1. 0 6. 6 4. 7 Katydid Grasshopper Katydids

Feature Generation • Feature generation refers to any technique to make new features from existing features • Recall pigeon problem 2, and assume we are using the linear classifier Pigeon Problem 2 Examples of class A Using both features works poorly, using just X works poorly, using just Y works poorly. . 4 4 5 5 6 3 Examples of class B 5 2 5 5 3 2. 5 3 10 9 8 7 6 5 4 3 2 1 1 2 3 4 5 6 7 8 9 10

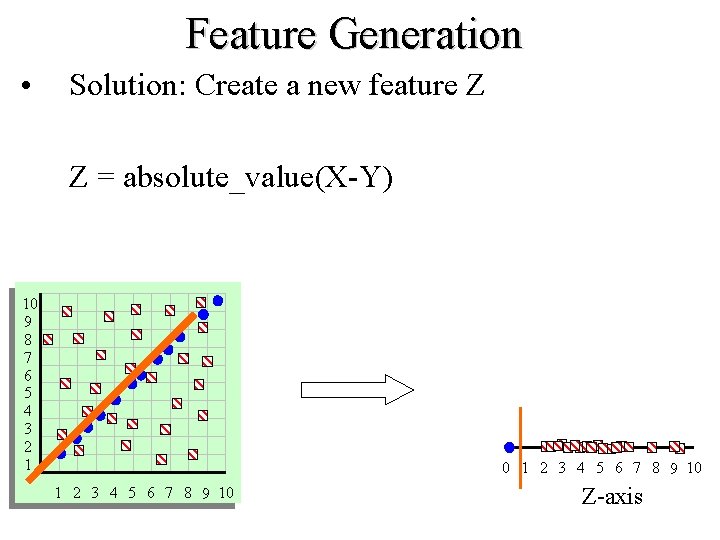
Feature Generation • Solution: Create a new feature Z Z = absolute_value(X-Y) 10 9 8 7 6 5 4 3 2 1 0 1 2 3 4 5 6 7 8 9 10 Z-axis

Recall this example? It was a teaching example to show that NN could use any distance measure It would not really work very well, unless we had LOTS more data… ID Name Class Greek 1 Gunopulos 2 Papadopoulos Greek 3 Kollios Greek 4 Dardanos Greek 5 Keogh Irish 6 Gough Irish 7 Greenhaugh Irish 8 Hadleigh Irish

Japanese Names AIKO AIMI AINA AIRI AKANE AKEMI AKIKO AKIRA AMI AOI ARATA ASUKA Irish Names ABERCROMBIE ABERNETHY ACKART ACKERMAN ACKERS ACKLAND ACTON ADAIR ADOLPH ALVIN ADLAM AFFLECK AMMADON

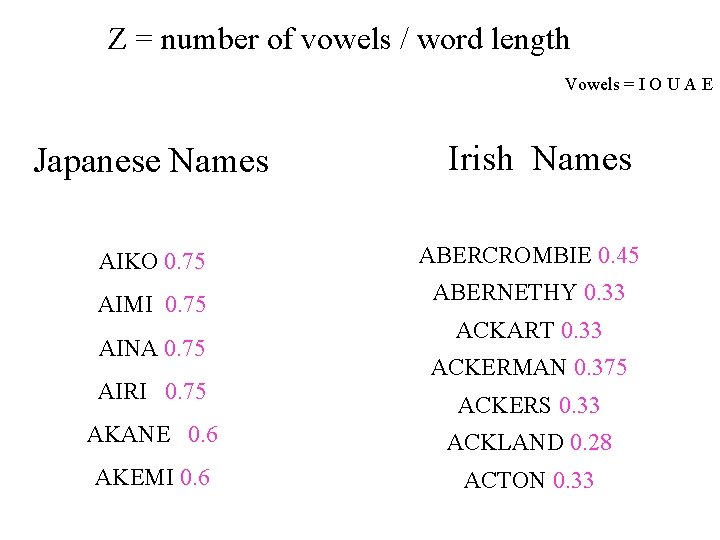
Z = number of vowels / word length Vowels = I O U A E Japanese Names Irish Names AIKO 0. 75 ABERCROMBIE 0. 45 AIMI 0. 75 ABERNETHY 0. 33 AINA 0. 75 AIRI 0. 75 ACKART 0. 33 ACKERMAN 0. 375 ACKERS 0. 33 AKANE 0. 6 ACKLAND 0. 28 AKEMI 0. 6 ACTON 0. 33

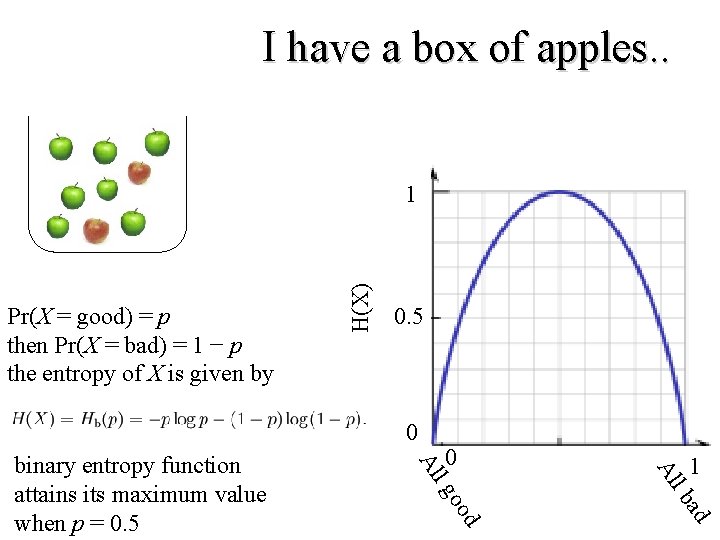
I have a box of apples. . Pr(X = good) = p then Pr(X = bad) = 1 − p the entropy of X is given by H(X) 1 0. 5 0 1 d oo ad lb Al 0 lg Al binary entropy function attains its maximum value when p = 0. 5

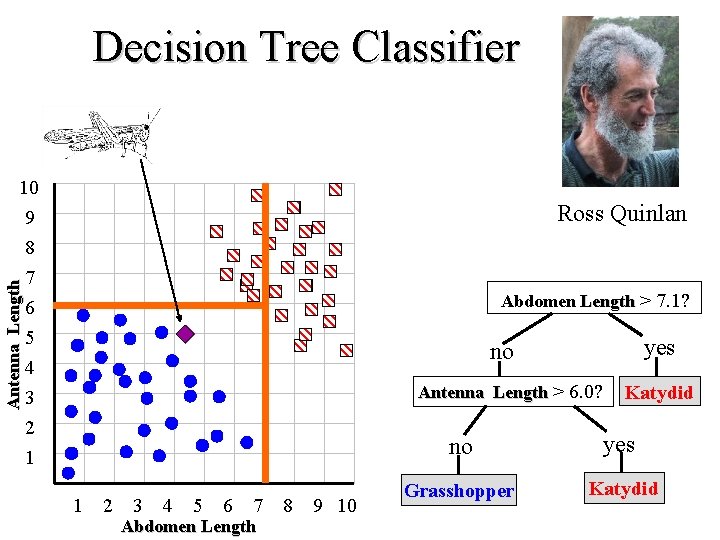
Decision Tree Classifier Antenna Length 10 Ross Quinlan 9 8 7 6 5 4 3 2 1 Abdomen Length > 7. 1? yes no Antenna Length > 6. 0? 1 2 3 4 5 6 7 Abdomen Length 8 9 10 Katydid no yes Grasshopper Katydid

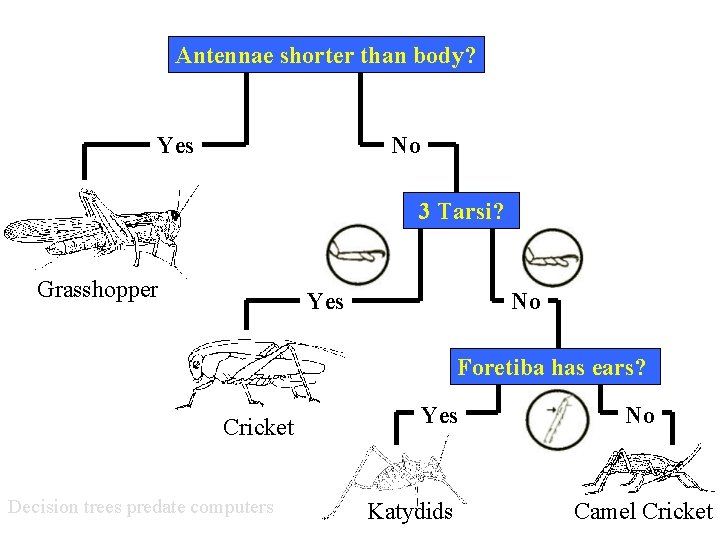
Antennae shorter than body? Yes No 3 Tarsi? Grasshopper Yes No Foretiba has ears? Cricket Decision trees predate computers Yes Katydids No Camel Cricket

Decision Tree Classification • Decision tree – – A flow-chart-like tree structure Internal node denotes a test on an attribute Branch represents an outcome of the test Leaf nodes represent class labels or class distribution • Decision tree generation consists of two phases – Tree construction • At start, all the training examples are at the root • Partition examples recursively based on selected attributes – Tree pruning • Identify and remove branches that reflect noise or outliers • Use of decision tree: Classifying an unknown sample – Test the attribute values of the sample against the decision tree

How do we construct the decision tree? • Basic algorithm (a greedy algorithm) – Tree is constructed in a top-down recursive divide-and-conquer manner – At start, all the training examples are at the root – Attributes are categorical (if continuous-valued, they can be discretized in advance) – Examples are partitioned recursively based on selected attributes. – Test attributes are selected on the basis of a heuristic or statistical measure (e. g. , information gain) • Conditions for stopping partitioning – All samples for a given node belong to the same class – There are no remaining attributes for further partitioning – majority voting is employed for classifying the leaf – There are no samples left

Information Gain as A Splitting Criteria • Select the attribute with the highest information gain (information gain is the expected reduction in entropy). • Assume there are two classes, P and N – Let the set of examples S contain p elements of class P and n elements of class N – The amount of information, needed to decide if an arbitrary example in S belongs to P or N is defined as 0 log(0) is defined as 0

Information Gain in Decision Tree Induction • Assume that using attribute A, a current set will be partitioned into some number of child sets • The encoding information that would be gained by branching on A Note: entropy is at its minimum if the collection of objects is completely uniform

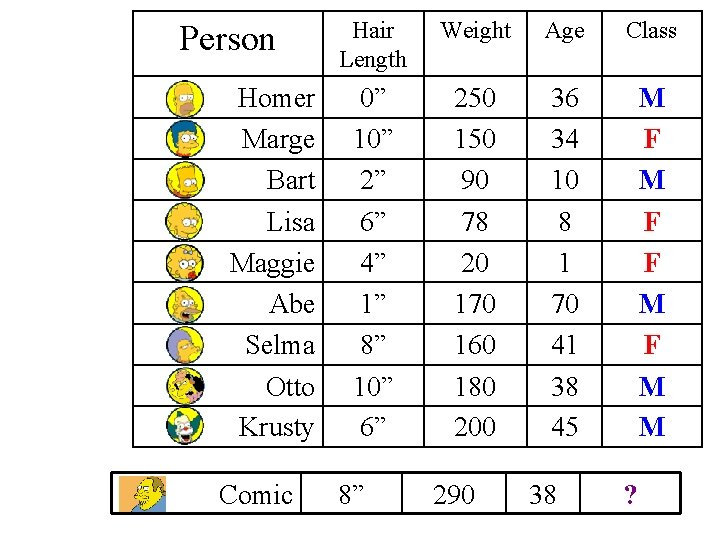
Person Homer Marge Bart Lisa Maggie Abe Selma Otto Krusty Comic Hair Length Weight Age Class 0” 10” 2” 6” 4” 1” 8” 10” 6” 250 150 90 78 20 170 160 180 200 36 34 10 8 1 70 41 38 45 M F F M M 8” 290 38 ?

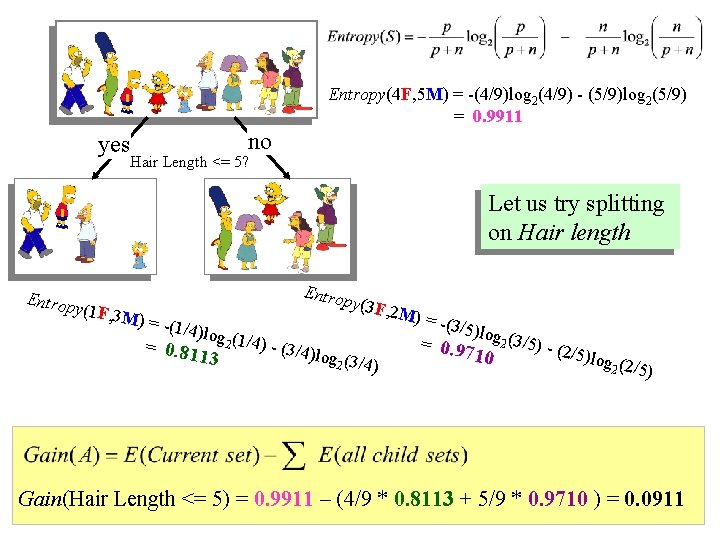
Entropy(4 F, 5 M) = -(4/9)log 2(4/9) - (5/9)log 2(5/9) = 0. 9911 yes no Hair Length <= 5? Let us try splitting on Hair length Entrop y(1 F, 3 M) = - Entro (1/4)lo py(3 F g = 0. 81 2 (1/4) - (3/4) log 2 (3/ 13 4) , 2 M) = -(3/ 5)log 2 (3/5) = 0. 9 (2 710 /5)log 2 (2/5) Gain(Hair Length <= 5) = 0. 9911 – (4/9 * 0. 8113 + 5/9 * 0. 9710 ) = 0. 0911

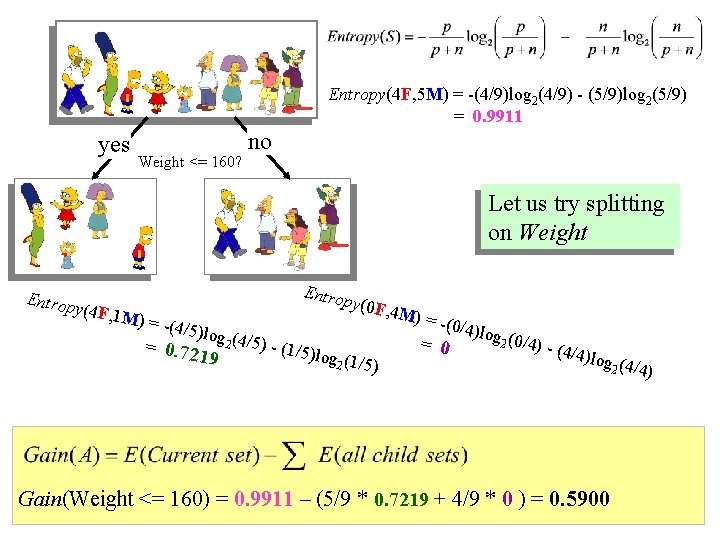
Entropy(4 F, 5 M) = -(4/9)log 2(4/9) - (5/9)log 2(5/9) = 0. 9911 yes Weight <= 160? no Let us try splitting on Weight Entrop y(4 F, 1 M) = - Entro (4/5)lo py(0 F g = 0. 72 2 (4/5) - (1/5) log 2 (1/ 19 5) , 4 M) = -(0/ 4)log 2 (0/4) = 0 (4 /4)log Gain(Weight <= 160) = 0. 9911 – (5/9 * 0. 7219 + 4/9 * 0 ) = 0. 5900 2 (4/4)

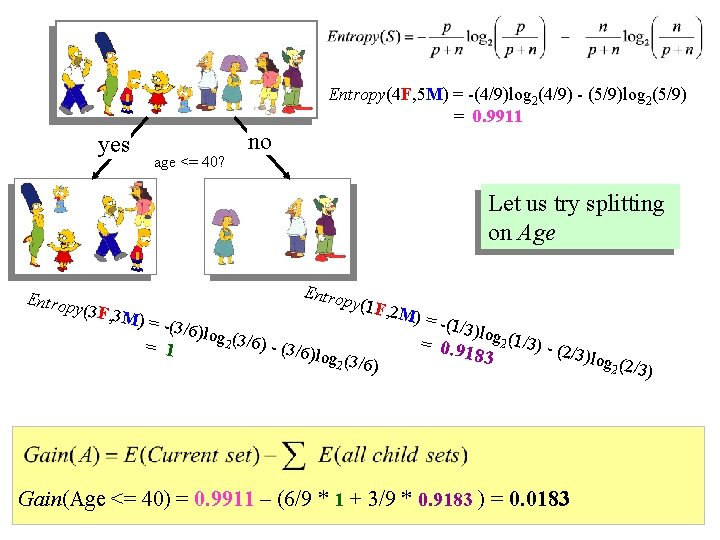
Entropy(4 F, 5 M) = -(4/9)log 2(4/9) - (5/9)log 2(5/9) = 0. 9911 yes age <= 40? no Let us try splitting on Age Entrop y(3 F, 3 M) = - Entro (3/6)lo = 1 py(1 F g 2 (3/6) - (3/6)l og 2 (3/6 ) , 2 M) = -(1/ 3)log 2 (1/3) = 0. 9 (2 183 Gain(Age <= 40) = 0. 9911 – (6/9 * 1 + 3/9 * 0. 9183 ) = 0. 0183 /3)log 2 (2/3)

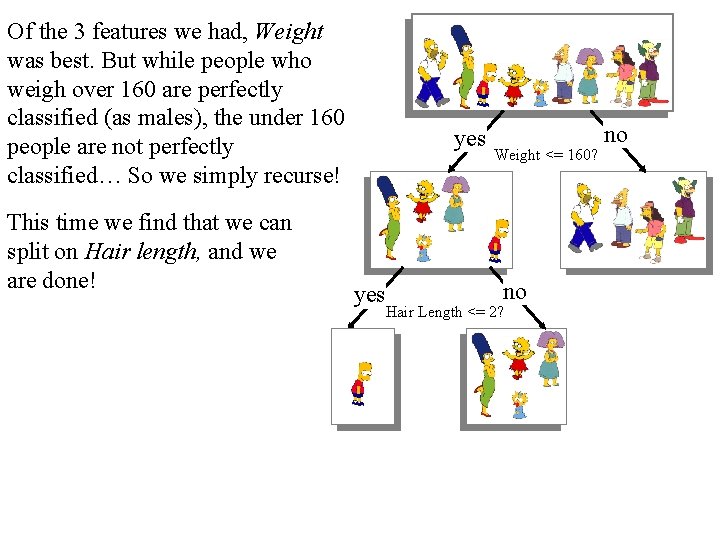
Of the 3 features we had, Weight was best. But while people who weigh over 160 are perfectly classified (as males), the under 160 people are not perfectly classified… So we simply recurse! This time we find that we can split on Hair length, and we are done! yes Weight <= 160? no Hair Length <= 2? no

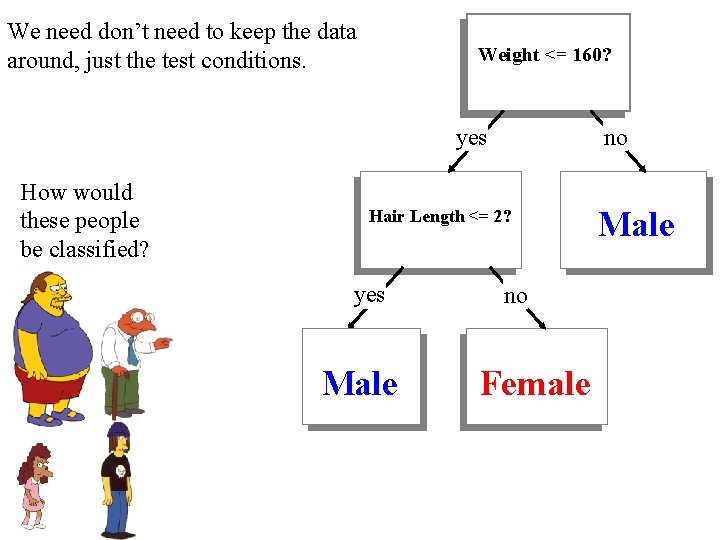
We need don’t need to keep the data around, just the test conditions. Weight <= 160? yes How would these people be classified? no Hair Length <= 2? yes Male no Female Male

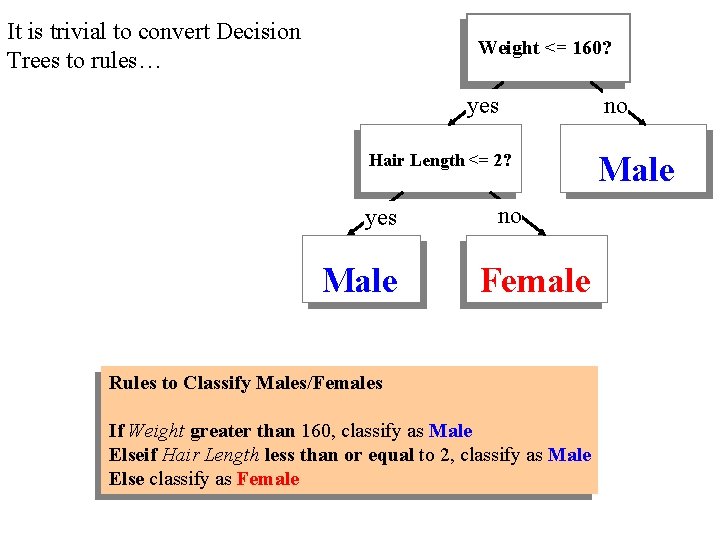
It is trivial to convert Decision Trees to rules… Weight <= 160? yes Hair Length <= 2? yes Male no Female Rules to Classify Males/Females If Weight greater than 160, classify as Male Elseif Hair Length less than or equal to 2, classify as Male Else classify as Female no Male

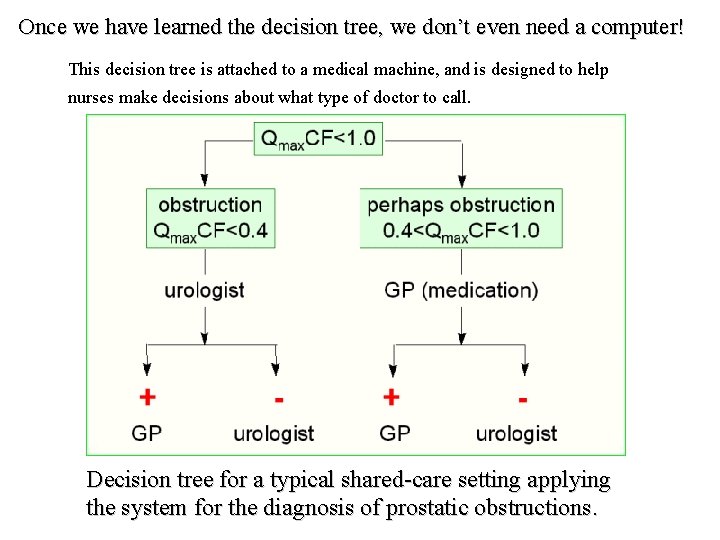
Once we have learned the decision tree, we don’t even need a computer! This decision tree is attached to a medical machine, and is designed to help nurses make decisions about what type of doctor to call. Decision tree for a typical shared-care setting applying the system for the diagnosis of prostatic obstructions.

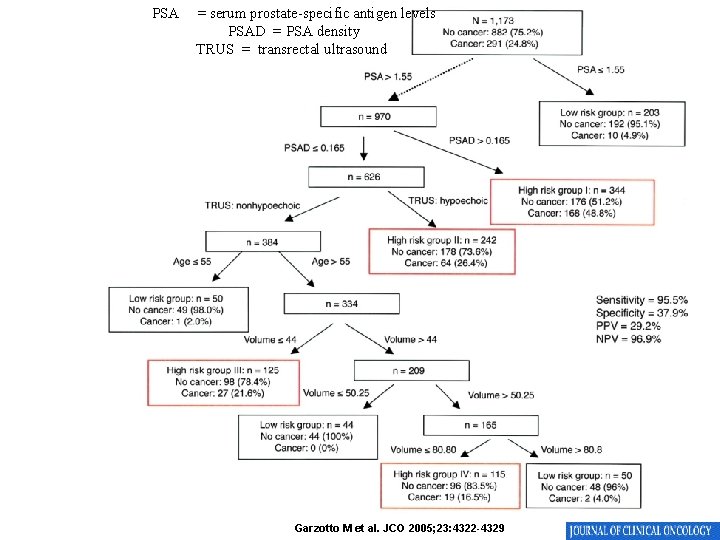
PSA = serum prostate-specific antigen levels PSAD = PSA density TRUS = transrectal ultrasound Garzotto M et al. JCO 2005; 23: 4322 -4329

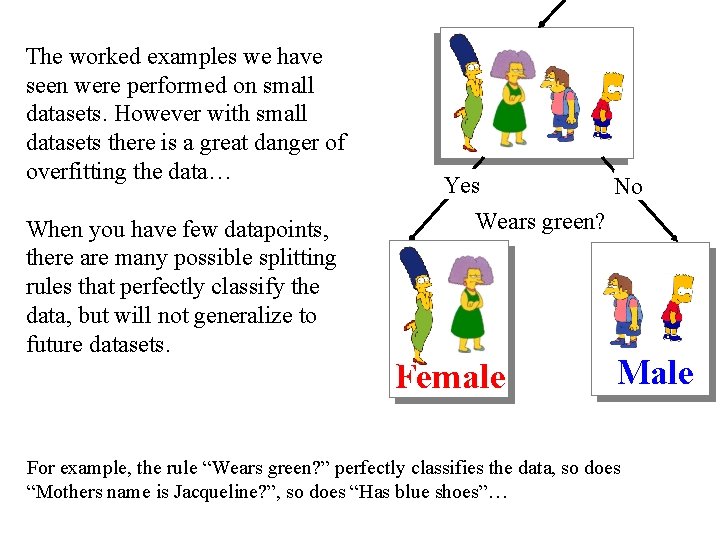
The worked examples we have seen were performed on small datasets. However with small datasets there is a great danger of overfitting the data… When you have few datapoints, there are many possible splitting rules that perfectly classify the data, but will not generalize to future datasets. Yes No Wears green? Female Male For example, the rule “Wears green? ” perfectly classifies the data, so does “Mothers name is Jacqueline? ”, so does “Has blue shoes”…

Avoid Overfitting in Classification • The generated tree may overfit the training data – Too many branches, some may reflect anomalies due to noise or outliers – Result is in poor accuracy for unseen samples • Two approaches to avoid overfitting – Prepruning: Halt tree construction early—do not split a node if this would result in the goodness measure falling below a threshold • Difficult to choose an appropriate threshold – Postpruning: Remove branches from a “fully grown” tree —get a sequence of progressively pruned trees • Use a set of data different from the training data to decide which is the “best pruned tree”

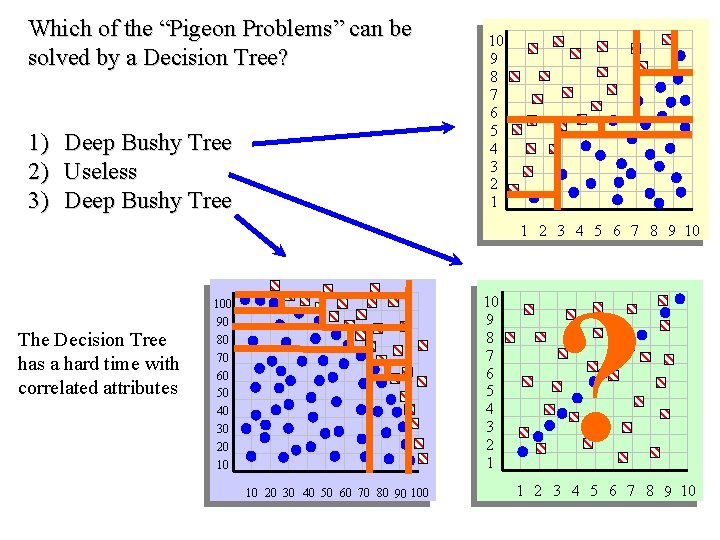
Which of the “Pigeon Problems” can be solved by a Decision Tree? 1) 2) 3) Deep Bushy Tree Useless Deep Bushy Tree 10 9 8 7 6 5 4 3 2 1 1 2 3 4 5 6 7 8 9 10 The Decision Tree has a hard time with correlated attributes 10 9 8 7 6 5 4 3 2 1 100 90 80 70 60 50 40 30 20 10 10 20 30 40 50 60 70 80 90 100 ? 1 2 3 4 5 6 7 8 9 10

Advantages/Disadvantages of Decision Trees • Advantages: – Easy to understand (Doctors love them!) – Easy to generate rules • Disadvantages: – May suffer from overfitting. – Classifies by rectangular partitioning (so does not handle correlated features very well). – Can be quite large – pruning is necessary. – Does not handle streaming data easily

There now exists, perhaps tens of million of digitized pages of historical manuscripts dating back to the 12 th century, that feature one or more heraldic shields The images are often stained, faded or torn

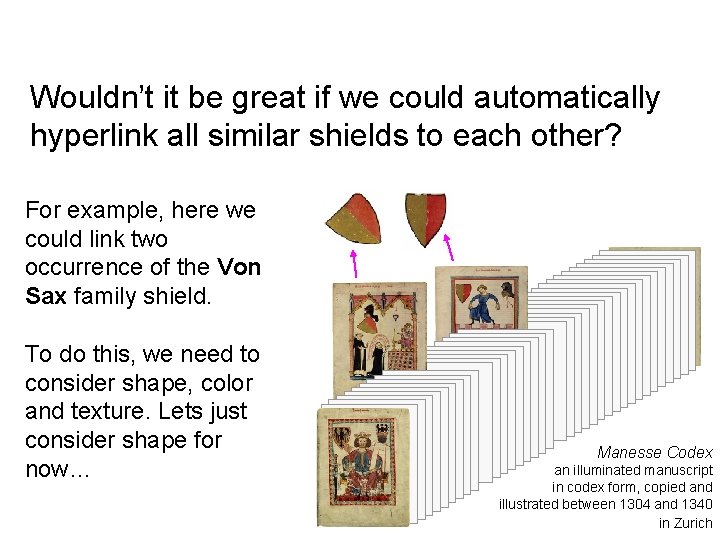
Wouldn’t it be great if we could automatically hyperlink all similar shields to each other? For example, here we could link two occurrence of the Von Sax family shield. To do this, we need to consider shape, color and texture. Lets just consider shape for now… Manesse Codex an illuminated manuscript in codex form, copied and illustrated between 1304 and 1340 in Zurich

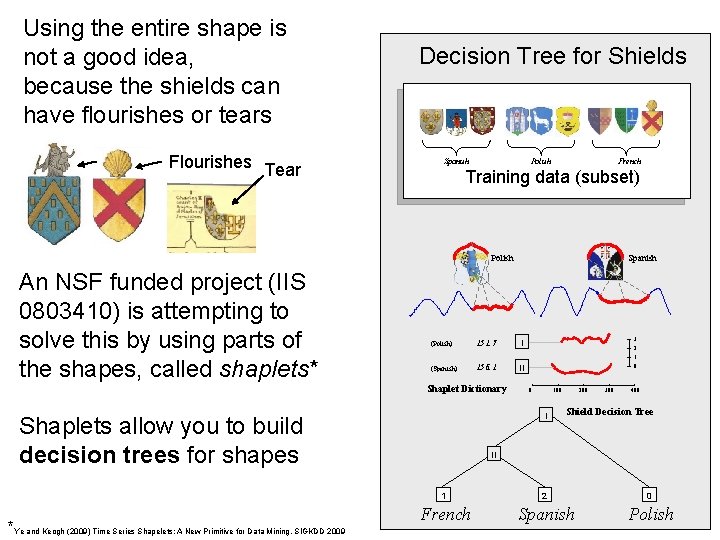
Using the entire shape is not a good idea, because the shields can have flourishes or tears Flourishes Tear Decision Tree for Shields Spanish Polish French Training data (subset) Polish An NSF funded project (IIS 0803410) is attempting to solve this by using parts of the shapes, called shaplets* (Polish) 151. 7 I (Spanish) 156. 1 II Shaplet Dictionary 3 2 1 0 0 100 200 300 400 I Shield Decision Tree 1 2 0 French Spanish Polish Shaplets allow you to build decision trees for shapes *Ye and Keogh (2009) Time Series Shapelets: A New Primitive for Data Mining. SIGKDD 2009 Spanish II

Naïve Bayes Classifier Thomas Bayes 1702 - 1761 We will start off with a visual intuition, before looking at the math…

Grasshoppers Katydids Antenna Length 10 9 8 7 6 5 4 3 2 1 1 2 3 4 5 6 7 Abdomen Length 8 9 10 Remember this example? Let’s get lots more data…

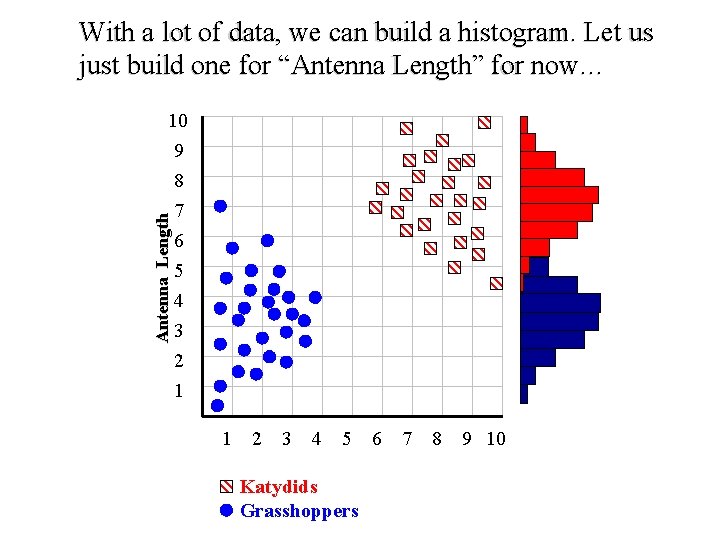
With a lot of data, we can build a histogram. Let us just build one for “Antenna Length” for now… Antenna Length 10 9 8 7 6 5 4 3 2 1 1 2 3 4 5 Katydids Grasshoppers 6 7 8 9 10

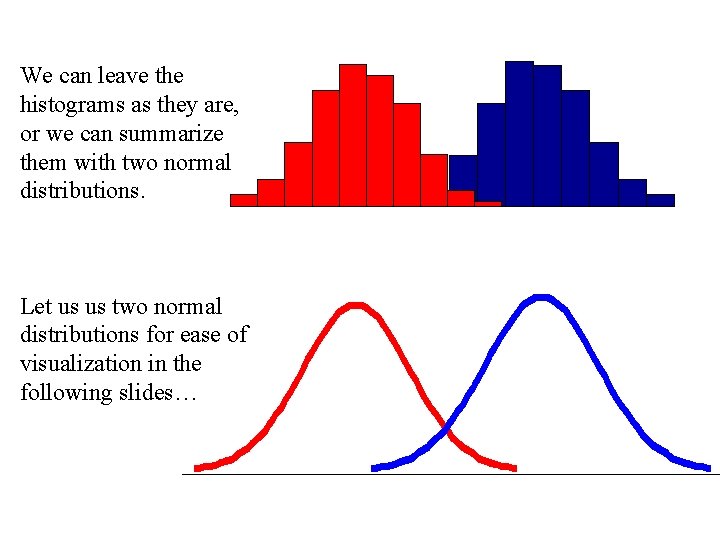
We can leave the histograms as they are, or we can summarize them with two normal distributions. Let us us two normal distributions for ease of visualization in the following slides…

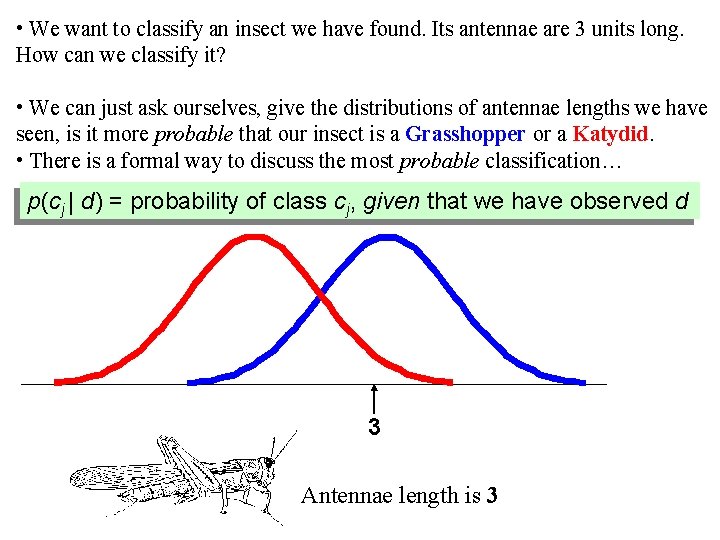
• We want to classify an insect we have found. Its antennae are 3 units long. How can we classify it? • We can just ask ourselves, give the distributions of antennae lengths we have seen, is it more probable that our insect is a Grasshopper or a Katydid. • There is a formal way to discuss the most probable classification… p(cj | d) = probability of class cj, given that we have observed d 3 Antennae length is 3

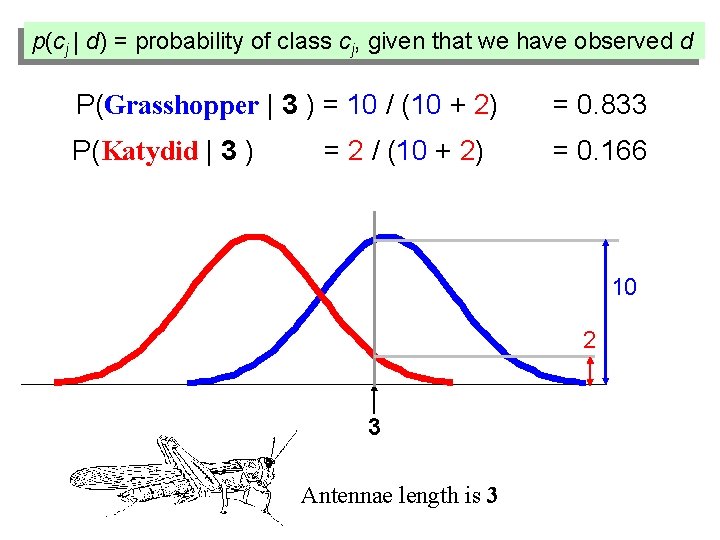
p(cj | d) = probability of class cj, given that we have observed d P(Grasshopper | 3 ) = 10 / (10 + 2) = 0. 833 P(Katydid | 3 ) = 0. 166 = 2 / (10 + 2) 10 2 3 Antennae length is 3

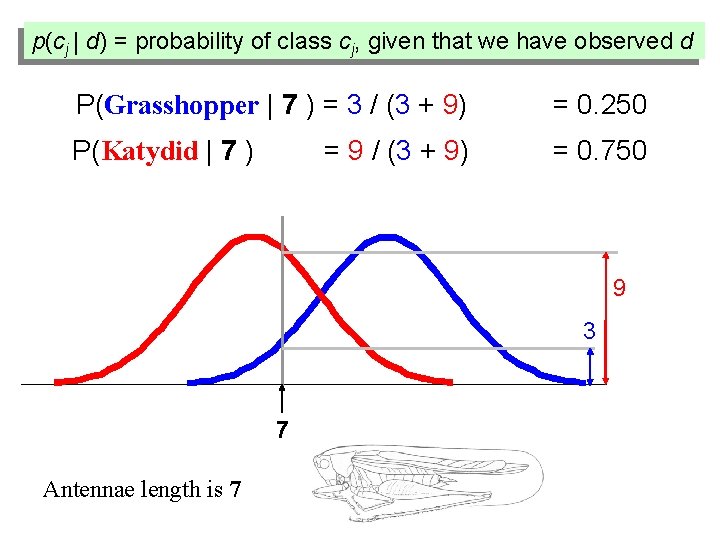
p(cj | d) = probability of class cj, given that we have observed d P(Grasshopper | 7 ) = 3 / (3 + 9) = 0. 250 P(Katydid | 7 ) = 0. 750 = 9 / (3 + 9) 9 3 7 Antennae length is 7

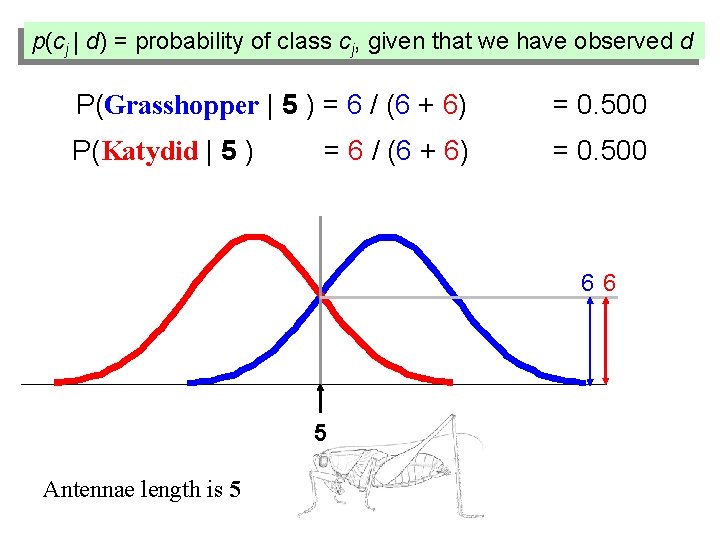
p(cj | d) = probability of class cj, given that we have observed d P(Grasshopper | 5 ) = 6 / (6 + 6) = 0. 500 P(Katydid | 5 ) = 0. 500 = 6 / (6 + 6) 66 5 Antennae length is 5

Bayes Classifiers That was a visual intuition for a simple case of the Bayes classifier, also called: • Idiot Bayes • Naïve Bayes • Simple Bayes We are about to see some of the mathematical formalisms, and more examples, but keep in mind the basic idea. Find out the probability of the previously unseen instance belonging to each class, then simply pick the most probable class.

Bayes Classifiers • Bayesian classifiers use Bayes theorem, which says p(cj | d ) = p(d | cj ) p(cj) p(d) • p(cj | d) = probability of instance d being in class cj, This is what we are trying to compute • p(d | cj) = probability of generating instance d given class cj, We can imagine that being in class cj, causes you to have feature d with some probability • p(cj) = probability of occurrence of class cj, This is just how frequent the class cj, is in our database • p(d) = probability of instance d occurring This can actually be ignored, since it is the same for all classes

Assume that we have two classes c 1 = male, male and c 2 = female (Note: “Drew can be a male or female name”) We have a person whose sex we do not know, say “drew” or d. Classifying drew as male or female is equivalent to asking is it more probable that drew is male or female, female I. e which is greater p(male | drew) or p(female | drew) Drew Barrymore Drew Carey What is the probability of being called “drew” given that you are a male? p(male | drew) = p(drew | male ) p(male) male p(drew) What is the probability of being a male? What is the probability of being named “drew”? (actually irrelevant, since it is that same for all classes)

This is Officer Drew (who arrested me in 1997). Is Officer Drew a Male or Female? Luckily, we have a small database with names and sex. We can use it to apply Bayes rule… Officer Drew p(cj | d) = p(d | cj ) p(cj) p(d) Name Drew Claudia Drew Sex Male Female Drew Alberto Karin Nina Female Male Female Sergio Male

Officer Drew p(cj | d) = p(d | cj ) p(cj) p(d) p(male | drew) = 1/3 * 3/8 p(female | drew) = 2/5 * 5/8 3/8 = 0. 125 3/8 = 0. 250 3/8 Name Drew Claudia Drew Sex Male Female Drew Alberto Karin Nina Sergio Female Male Officer Drew is more likely to be a Female

Officer Drew IS a female! Officer Drew p(male | drew) = 1/3 * 3/8 p(female | drew) = 2/5 * 5/8 3/8 = 0. 125 3/8 = 0. 250 3/8

So far we have only considered Bayes Classification when we have one attribute (the “antennae length”, or the “name”). But we may have many features. How do we use all the features? Name Drew Claudia Drew Over 170 CM No Yes No p(cj | d) = p(d | cj ) p(cj) p(d) Eye Blue Brown Blue Hair length Short Long Sex Male Female Drew Alberto Karin Nina No Yes Blue Brown Long Short Female Male Female Sergio Yes Blue Long Male

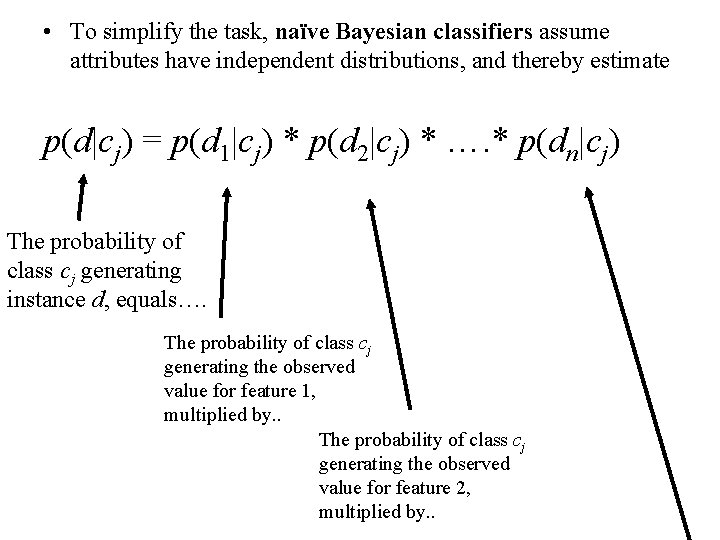
• To simplify the task, naïve Bayesian classifiers assume attributes have independent distributions, and thereby estimate p(d|cj) = p(d 1|cj) * p(d 2|cj) * …. * p(dn|cj) The probability of class cj generating instance d, equals…. The probability of class cj generating the observed value for feature 1, multiplied by. . The probability of class cj generating the observed value for feature 2, multiplied by. .

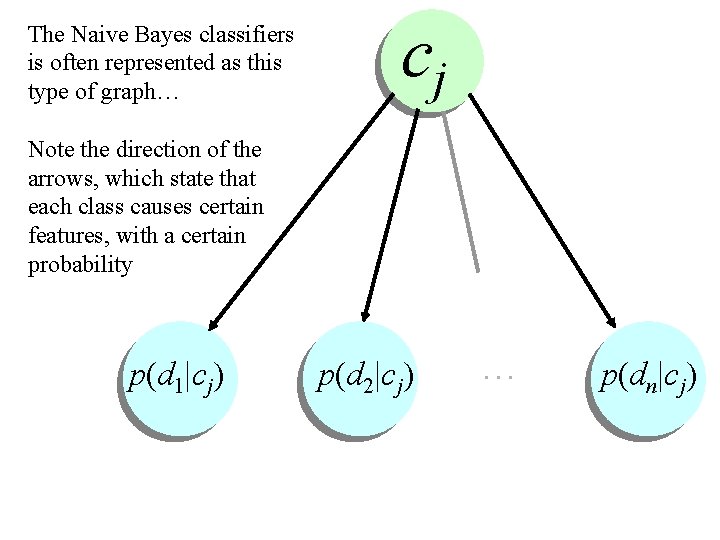
The Naive Bayes classifiers is often represented as this type of graph… cj Note the direction of the arrows, which state that each class causes certain features, with a certain probability p(d 1|cj) p(d 2|cj) … p(dn|cj)

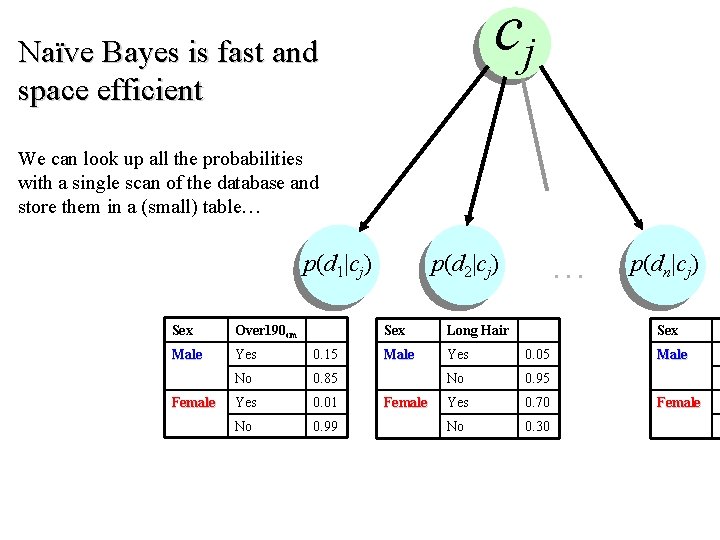
cj Naïve Bayes is fast and space efficient We can look up all the probabilities with a single scan of the database and store them in a (small) table… p(d 1|cj) Sex Over 190 cm Male Yes 0. 15 No 0. 85 Yes 0. 01 No 0. 99 Female … p(d 2|cj) Sex Long Hair Male Yes 0. 05 No 0. 95 Yes 0. 70 No 0. 30 Female p(dn|cj) Sex Male Female

Naïve Bayes is NOT sensitive to irrelevant features. . . Suppose we are trying to classify a persons sex based on several features, including eye color. (Of course, eye color is completely irrelevant to a persons gender) p(Jessica |cj) = p(eye = brown|cj) * p( wears_dress = yes|cj) * …. p(Jessica | Female) Female = 9, 000/10, 000 p(Jessica | Male) Male = 9, 001/10, 000 * 9, 975/10, 000 * …. * 2/10, 000 * …. Almost the same! However, this assumes that we have good enough estimates of the probabilities, so the more data the better.

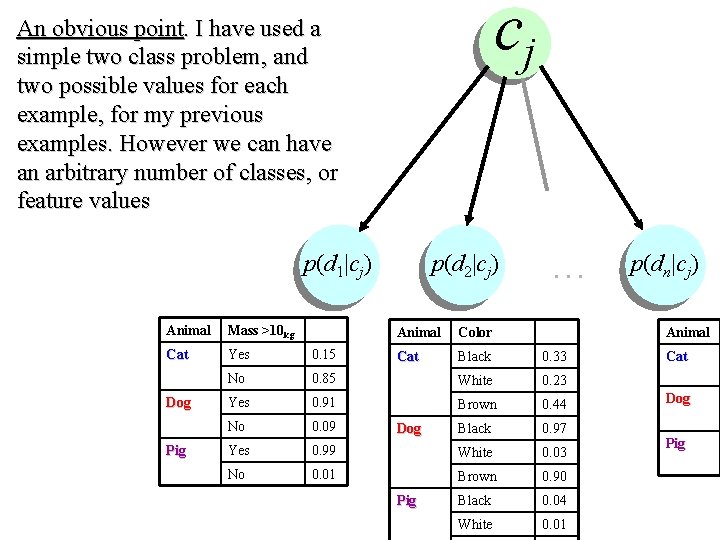
cj An obvious point. I have used a simple two class problem, and two possible values for each example, for my previous examples. However we can have an arbitrary number of classes, or feature values p(d 1|cj) Animal Mass >10 kg Cat Yes 0. 15 No Dog Pig p(d 2|cj) … Animal Color Cat Black 0. 33 0. 85 White 0. 23 Yes 0. 91 Brown 0. 44 No 0. 09 Black 0. 97 Yes 0. 99 White 0. 03 No 0. 01 Brown 0. 90 Black 0. 04 White 0. 01 Dog Pig p(dn|cj) Cat Dog Pig

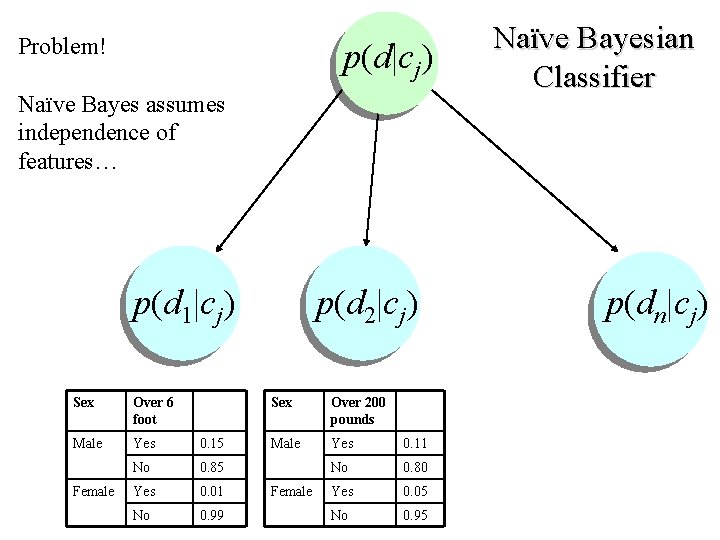
Problem! p(d|cj) Naïve Bayes assumes independence of features… p(d 1|cj) Sex Over 6 foot Male Yes 0. 15 No 0. 85 Yes 0. 01 No 0. 99 Female p(d 2|cj) Sex Over 200 pounds Male Yes 0. 11 No 0. 80 Yes 0. 05 No 0. 95 Female Naïve Bayesian Classifier p(dn|cj)

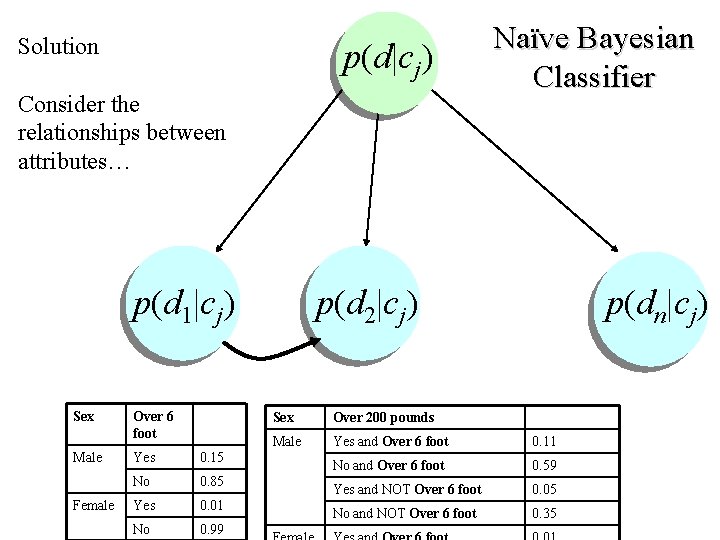
Solution p(d|cj) Consider the relationships between attributes… p(d 1|cj) Sex Male Female Over 6 foot Yes 0. 15 No 0. 85 Yes 0. 01 No 0. 99 Naïve Bayesian Classifier p(d 2|cj) p(dn|cj) Sex Over 200 pounds Male Yes and Over 6 foot 0. 11 No and Over 6 foot 0. 59 Yes and NOT Over 6 foot 0. 05 No and NOT Over 6 foot 0. 35

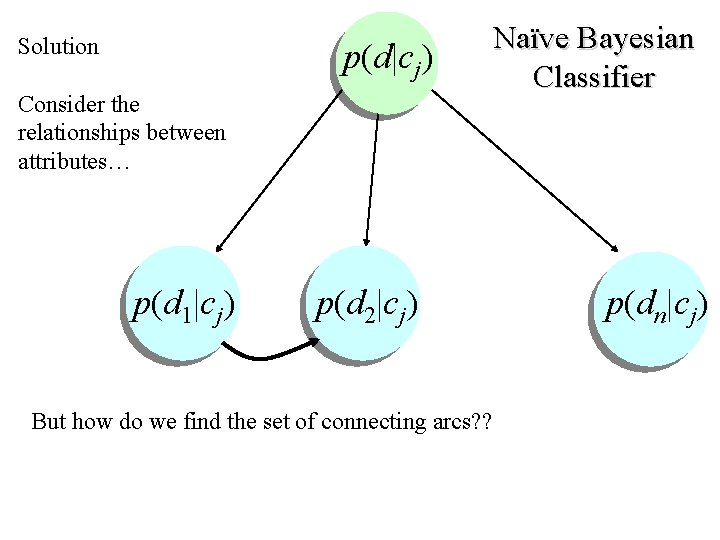
Solution p(d|cj) Consider the relationships between attributes… p(d 1|cj) p(d 2|cj) But how do we find the set of connecting arcs? ? Naïve Bayesian Classifier p(dn|cj)

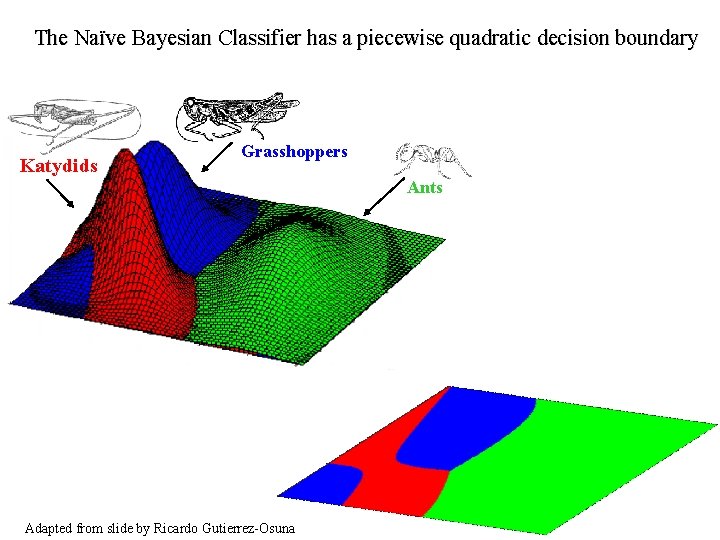
The Naïve Bayesian Classifier has a piecewise quadratic decision boundary Katydids Grasshoppers Ants Adapted from slide by Ricardo Gutierrez-Osuna

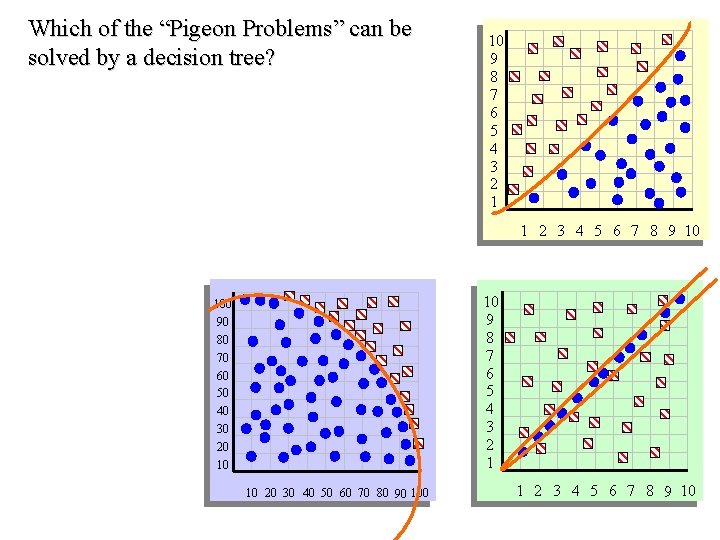
Which of the “Pigeon Problems” can be solved by a decision tree? 10 9 8 7 6 5 4 3 2 1 1 2 3 4 5 6 7 8 9 10 10 9 8 7 6 5 4 3 2 1 100 90 80 70 60 50 40 30 20 10 10 20 30 40 50 60 70 80 90 100 1 2 3 4 5 6 7 8 9 10

Dear SIR, I am Mr. John Coleman and my sister is Miss Rose Colemen, we are the children of late Chief Paul Colemen from Sierra Leone. I am writing you in absolute confidence primarily to seek your assistance to transfer our cash of twenty one Million Dollars ($21, 000. 00) now in the custody of a private Security trust firm in Europe the money is in trunk boxes deposited and declared as family valuables by my late father as a matter of fact the company does not know the content as money, although my father made them to under stand that the boxes belongs to his foreign partner. …

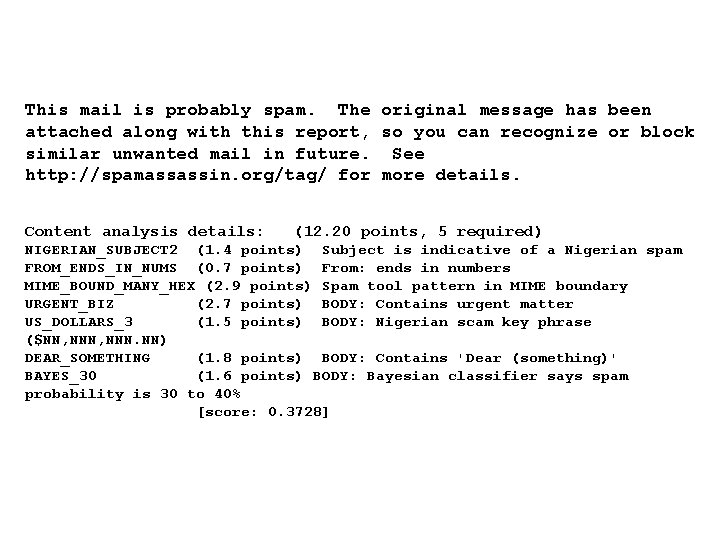
This mail is probably spam. The original message has been attached along with this report, so you can recognize or block similar unwanted mail in future. See http: //spamassassin. org/tag/ for more details. Content analysis details: (12. 20 points, 5 required) NIGERIAN_SUBJECT 2 (1. 4 points) Subject is indicative of a Nigerian spam FROM_ENDS_IN_NUMS (0. 7 points) From: ends in numbers MIME_BOUND_MANY_HEX (2. 9 points) Spam tool pattern in MIME boundary URGENT_BIZ (2. 7 points) BODY: Contains urgent matter US_DOLLARS_3 (1. 5 points) BODY: Nigerian scam key phrase ($NN, NNN. NN) DEAR_SOMETHING (1. 8 points) BODY: Contains 'Dear (something)' BAYES_30 (1. 6 points) BODY: Bayesian classifier says spam probability is 30 to 40% [score: 0. 3728]

Advantages/Disadvantages of Naïve Bayes • Advantages: – Fast to train (single scan). Fast to classify – Not sensitive to irrelevant features – Handles real and discrete data – Handles streaming data well • Disadvantages: – Assumes independence of features

Summary of Classification We have seen 4 major classification techniques: • Simple linear classifier, Nearest neighbor, Decision tree. There are other techniques: • Neural Networks, Support Vector Machines, Genetic algorithms. . In general, there is no one best classifier for all problems. You have to consider what you hope to achieve, and the data itself… Let us now move on to the other classic problem of data mining and machine learning, Clustering…