Over Lesson 4 3 Write a congruence statement

Over Lesson 4– 3 Write a congruence statement for the triangles. A. ΔLMN ΔRTS B. ΔLMN ΔSTR C. ΔLMN ΔRST D. ΔLMN ΔTRS

Over Lesson 4– 3 Name the corresponding congruent angles for the congruent triangles. A. L R, N T, M S B. L R, M S, N T C. L T, M R, N S D. L R, N S, M T

Over Lesson 4– 3 Name the corresponding congruent sides for the congruent triangles. ___ ___ ___ ___ ___ ___ A. LM RT, LN RS, NM ST B. LM RT, LN LR, LM LS C. LM ST, LN RT, NM RS ___ D. LM LN, RT RS, MN ST

Over Lesson 4– 3 Refer to the figure. Find x. A. 1 B. 2 C. 3 D. 4

Over Lesson 4– 3 Refer to the figure. Find m A. A. 30 B. 39 C. 59 D. 63

Over Lesson 4– 3 Given that ΔABC ΔDEF, which of the following statements is true? A. A E B. C D ___ ___ C. AB DE D. BC FD

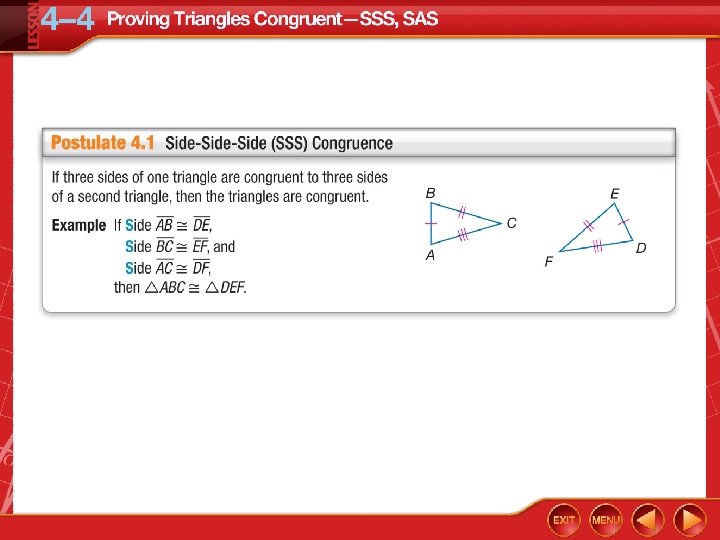
You proved triangles congruent using the definition of congruence. • Use the SSS Postulate to test for triangle congruence. • Use the SAS Postulate to test for triangle congruence.

• included angle

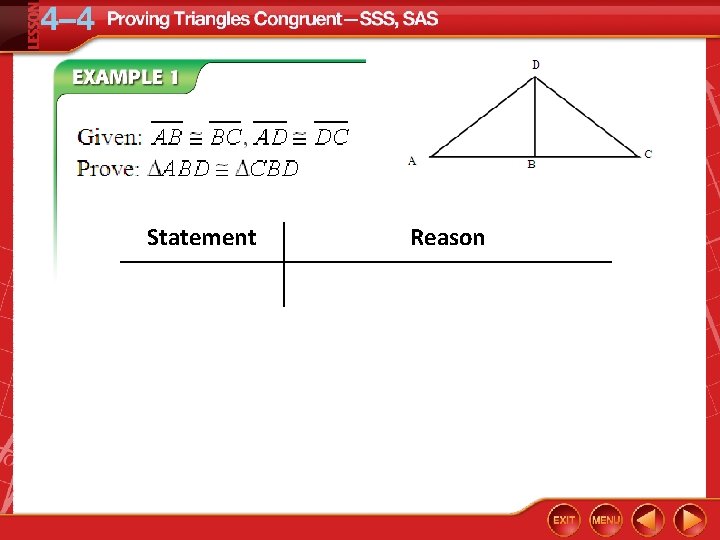
Use SSS to Prove Triangles Congruent Statement Reason

Statement Reason

Which information ___ is missing from the flowproof? Given: AC AB D is the midpoint of BC. Prove: ΔADC ΔADB ___ ___ A. AC B. AB C. AD D. CB BC

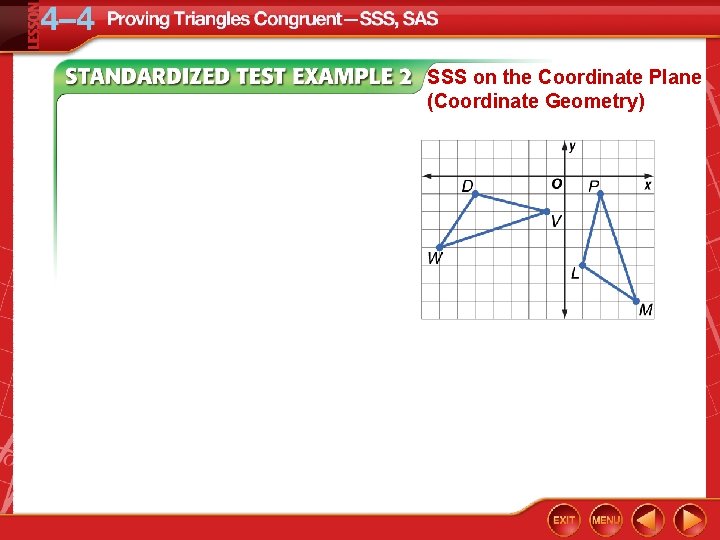
SSS on the Coordinate Plane EXTENDED RESPONSE Triangle DVW has vertices D(– 5, – 1), V(– 1, – 2), and W(– 7, – 4). Triangle LPM has vertices L(1, – 5), P(2, – 1), and M(4, – 7). a. Graph both triangles on the same coordinate plane. b. Prove the triangles are congruent by SSS using coordinate geometry. You must show work!

SSS on the Coordinate Plane (Coordinate Geometry)

Determine whether ΔABC ΔDEF for A(– 5, 5), B(0, 3), C(– 4, 1), D(6, – 3), E(1, – 1), and F(5, 1). A. yes B. no C. cannot be determined

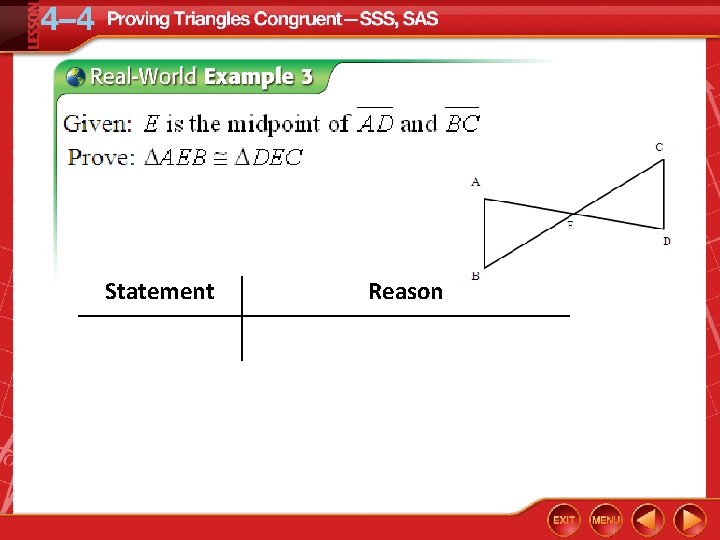
Use SAS to Prove Triangles are Congruent ENTOMOLOGY The wings of one type of moth form two triangles. Write a two-column proof to prove that ΔFEG ΔHIG if EI FH, and G is the midpoint of both EI and FH.

Use SAS to Prove Triangles are Congruent Given: EI FH; G is the midpoint of both EI and FH. Prove: ΔFEG ΔHIG Proof: Statements 1. EI FH; G is the midpoint of EI; G is the midpoint of FH. Reasons 1. Given

Statement Reason

The two-column proof is shown to prove that ΔABG ΔCGB if ABG CGB and AB CG. Choose the best reason to fill in the blank. Proof: Statements 1. Reasons 1. Given 2. ? Property 3. ΔABG ΔCGB A. Reflexive 3. SAS Postulate B. Symmetric C. Transitive D. Substitution

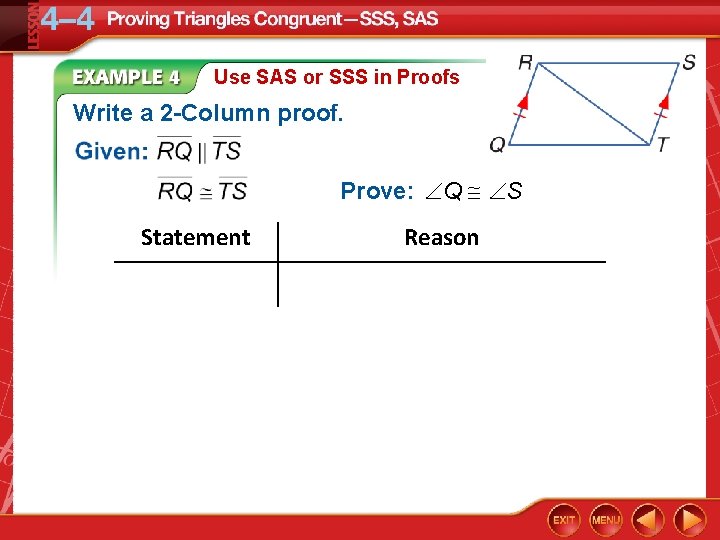
Use SAS or SSS in Proofs Write a 2 -Column proof. Prove: Q S Statement Reason

Choose the correct reason to complete the following flow proof. A. Segment Addition Postulate B. Symmetric Property C. Midpoint Theorem D. Substitution