Over Chapter 1 Identify the parent function f

You analyzed parent functions and their families of graphs. (Lesson 1 -5) • Graph

• power function • monomial function • radical function • extraneous solution

Analyze Monomial Functions A. Graph and analyze . Describe the domain, range, intercepts, end

Analyze Monomial Functions D = (–∞, ∞); R = [0, ∞); intercept: 0; end

Analyze Monomial Functions Answer: D = (–∞, ∞); R = [0, ∞); intercept: 0;

Analyze Monomial Functions B. Graph and analyze f (x) = –x 5. Describe the

Analyze Monomial Functions D = (–∞, ∞); R = (–∞, ∞); intercept: 0; end

Analyze Monomial Functions Answer: D = (–∞, ∞); R = (–∞, ∞); intercept: 0;

Describe where the graph of the function f (x) = 2 x 4 is

Functions with Negative Exponents A. Graph and analyze f (x) = 2 x –

Functions with Negative Exponents intercept: none; end behavior: continuity: infinite discontinuity at x =

Functions with Negative Exponents Answer: D = (– ∞, 0) (0, ∞); R =

Functions with Negative Exponents B. Graph and analyze f (x) = 2 x –

Functions with Negative Exponents D = (–∞, 0) (0, ∞); R = (–∞, 0)

Describe the end behavior of the graph of f (x) = 3 x –

Rational Exponents A. Graph and analyze. Describe the domain, range, intercepts, end behavior, continuity,

Rational Exponents D = [0, ∞); R = [0, ∞); intercept: 0; end behavior:

Rational Exponents Answer: D = [0, ∞); R = [0, ∞); intercept: 0; ;

Rational Exponents B. Graph and analyze. Describe the domain, range, intercepts, end behavior, continuity,

Rational Exponents D = (0, ∞); R = (0, ∞); intercept: none; end behavior:

Rational Exponents Answer: D = (0, ∞); R = (0, ∞); no intercept ;

Describe the continuity of the function A. continuous for all real numbers B. continuous

Power Regression A. ANIMALS The following data represent the body length L in centimeters

Power Regression Answer: The scatter plot appears to resemble the square root function which

Power Regression B. ANIMALS The following data represent the body length L in centimeters

Power Regression Using the Pwr. Reg tool on a graphing calculator yields y =

Power Regression C. ANIMALS The following data represent the body length L in centimeters

Power Regression Use the CALC feature on the calculator to find f(77). The value

AIR The table shows the amount of air f(r) in cubic inches needed to

Graph Radical Functions A. Graph and analyze. Describe the domain, range, intercepts, end behavior,

Graph Radical Functions D = [0, ∞); R = [0, ∞); intercept: 0; continuous

Graph Radical Functions Answer: D = [0, ∞); R = [0, ∞); intercept: 0;

Graph Radical Functions B. Graph and analyze . Describe the domain, range, intercepts, end

Graph Radical Functions D = (–∞, ∞); R = (–∞, ∞); x-intercept: , y-intercept:

Graph Radical Functions Answer: D = (–∞, ∞) ; R = (–∞, ∞) ;

Find the intercepts of the graph of A. x-intercept: B. x-intercepts: C. x-intercept: D.

Solve Radical Equations A. Solve . original equation Isolate the radical. Square each side

Solve Radical Equations Answer: – 1, 5 Check x=5 10 = 10 x =

Solve Radical Equations B. Solve . original equation Subtract 8 from each side. Raise

Solve Radical Equations C. Solve . original equation Square each side. Isolate the radical.

Solve Radical Equations x= 8 x = 24 Solve. One solution checks and the

Solve A. 0, 5 B. 11, – 11 C. 11 D. 0, 11 .

Slides: 54

Download presentation

Over Chapter 1 Identify the parent function f (x) of g (x) = 2|x – 3| + 1. Describe how the graphs of g (x) and f (x) are related. A. f (x) = | x |; f (x) is translated 3 units right, 1 unit up and expanded vertically to graph g (x). B. f (x) = | x |; f (x) is translated 3 units right, 1 unit up and expanded horizontally to graph g (x). C. f (x) = | x |; f (x) is translated 3 units left, 1 unit up and expanded vertically to graph g (x). D. f (x) = | x |; f (x) is translated 3 units left, 1 unit down and expanded horizontally to graph g (x).

You analyzed parent functions and their families of graphs. (Lesson 1 -5) • Graph and analyze power functions. • Graph and analyze radical functions, and solve radical equations.

• power function • monomial function • radical function • extraneous solution

Analyze Monomial Functions A. Graph and analyze . Describe the domain, range, intercepts, end behavior, continuity, and where the function is increasing or decreasing. Evaluate the function for several x-values in its domain. Then use a smooth curve to connect each of these points to complete the graph.

Analyze Monomial Functions D = (–∞, ∞); R = [0, ∞); intercept: 0; end behavior: continuity: continuous for all real numbers; decreasing: (–∞, 0); increasing: (0, ∞)

Analyze Monomial Functions Answer: D = (–∞, ∞); R = [0, ∞); intercept: 0; continuous for all real numbers; decreasing: (–∞, 0) , increasing: (0, ∞)

Analyze Monomial Functions B. Graph and analyze f (x) = –x 5. Describe the domain, range, intercepts, end behavior, continuity, and where the function is increasing or decreasing.

Analyze Monomial Functions D = (–∞, ∞); R = (–∞, ∞); intercept: 0; end behavior: continuity: continuous for all real numbers; decreasing: (–∞, ∞)

Analyze Monomial Functions Answer: D = (–∞, ∞); R = (–∞, ∞); intercept: 0; continuous for all real numbers; decreasing: (–∞, ∞)

Describe where the graph of the function f (x) = 2 x 4 is increasing or decreasing. A. increasing: (–∞, ∞) B. decreasing: (–∞, 0) , increasing: (0, ∞) C. decreasing: (–∞, ∞) D. increasing: (–∞, 0), decreasing: (0, ∞)

Functions with Negative Exponents A. Graph and analyze f (x) = 2 x – 4. Describe the domain, range, intercepts, end behavior, continuity, and where the function is increasing or decreasing.

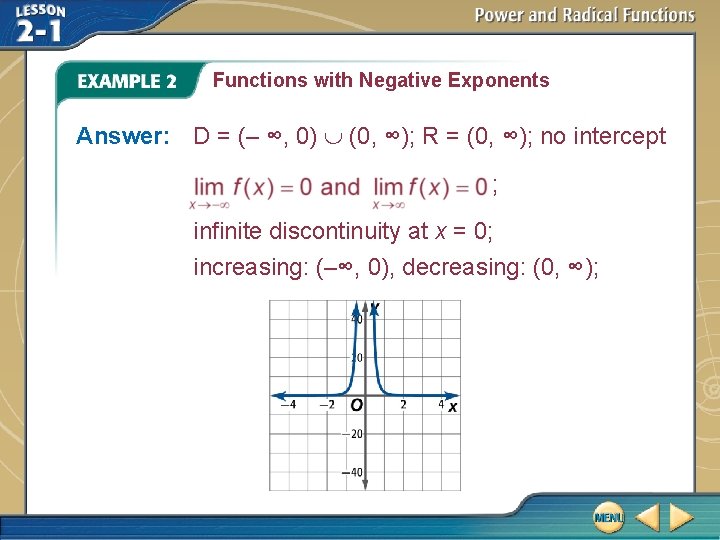
Functions with Negative Exponents intercept: none; end behavior: continuity: infinite discontinuity at x = 0; increasing: (–∞, 0); decreasing: (0, ∞)

Functions with Negative Exponents Answer: D = (– ∞, 0) (0, ∞); R = (0, ∞); no intercept ; infinite discontinuity at x = 0; increasing: (–∞, 0), decreasing: (0, ∞);

Functions with Negative Exponents B. Graph and analyze f (x) = 2 x – 3. Describe the domain, range, intercepts, end behavior, continuity, and where the function is increasing or decreasing.

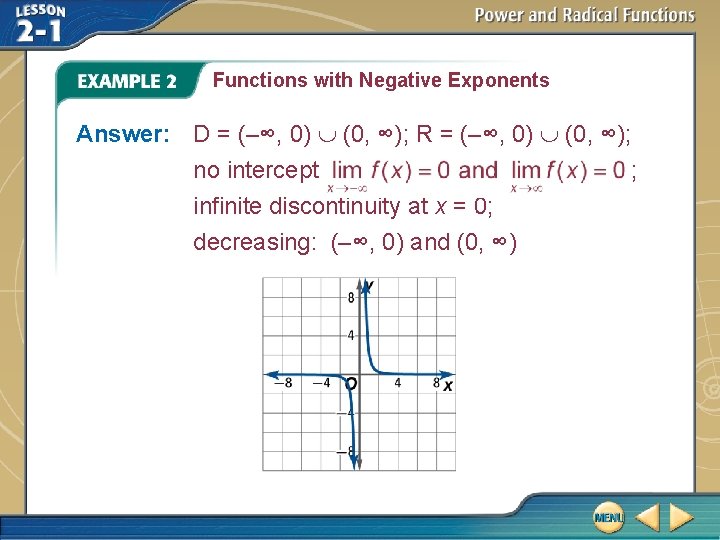
Functions with Negative Exponents D = (–∞, 0) (0, ∞); R = (–∞, 0) (0, ∞); intercept: none; end behavior: continuity: infinite discontinuity at x = 0; decreasing: (–∞, 0) and (0, ∞)

Functions with Negative Exponents Answer: D = (–∞, 0) (0, ∞); R = (–∞, 0) (0, ∞); no intercept ; infinite discontinuity at x = 0; decreasing: (–∞, 0) and (0, ∞)

Describe the end behavior of the graph of f (x) = 3 x – 5. A. B. C. D.

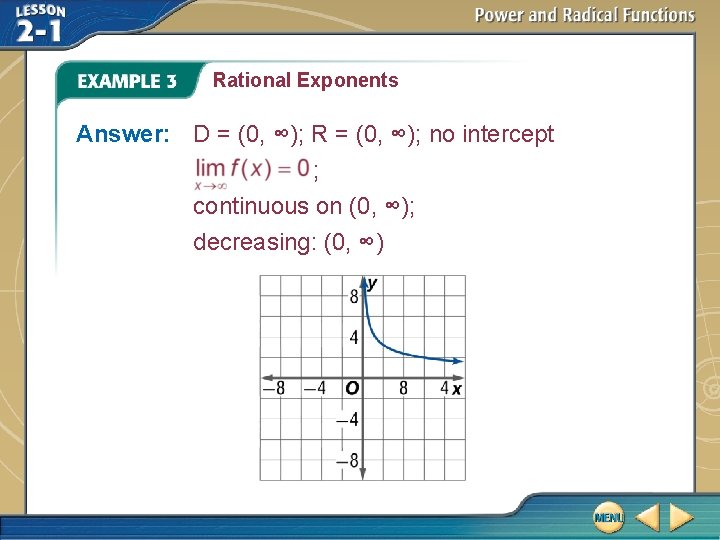
Rational Exponents A. Graph and analyze. Describe the domain, range, intercepts, end behavior, continuity, and where the function is increasing or decreasing.

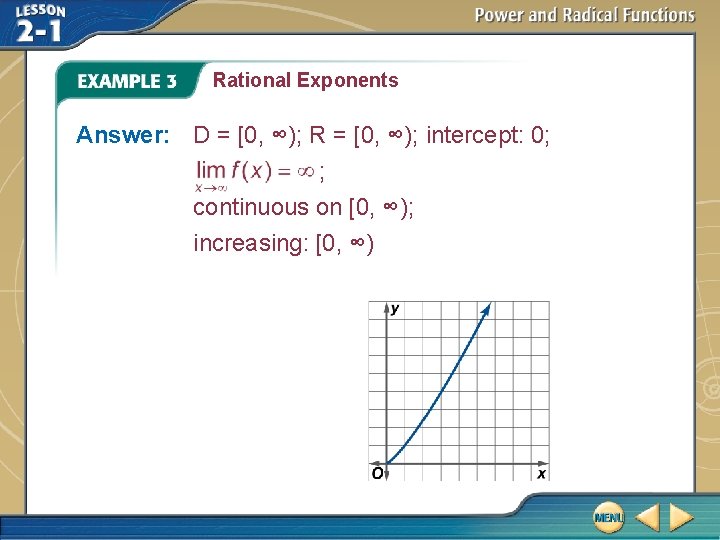
Rational Exponents D = [0, ∞); R = [0, ∞); intercept: 0; end behavior: continuity: continuous on [0, ∞); increasing: [0, ∞)

Rational Exponents Answer: D = [0, ∞); R = [0, ∞); intercept: 0; ; continuous on [0, ∞); increasing: [0, ∞)

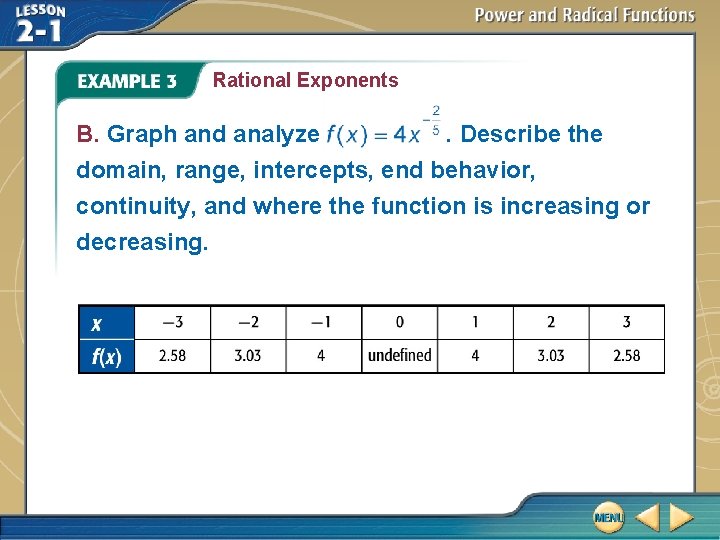
Rational Exponents B. Graph and analyze. Describe the domain, range, intercepts, end behavior, continuity, and where the function is increasing or decreasing.

Rational Exponents D = (0, ∞); R = (0, ∞); intercept: none; end behavior: continuity: continuous on (0, ∞); decreasing: (0, ∞)

Rational Exponents Answer: D = (0, ∞); R = (0, ∞); no intercept ; continuous on (0, ∞); decreasing: (0, ∞)

Describe the continuity of the function A. continuous for all real numbers B. continuous on C. continuous on (0, ∞] D. continuous on [0, ∞) and .

Power Regression A. ANIMALS The following data represent the body length L in centimeters and the mass M in kilograms of several African Golden cats being studied by a scientist. Create a scatter plot of the data.

Power Regression Answer: The scatter plot appears to resemble the square root function which is a power function.

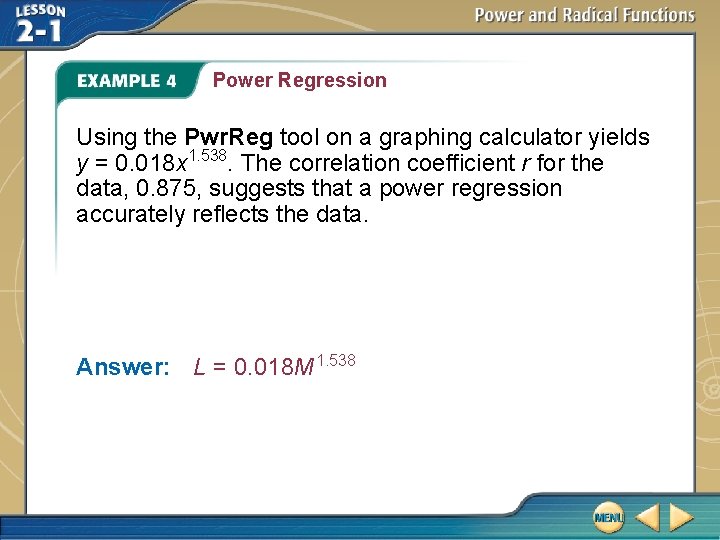
Power Regression B. ANIMALS The following data represent the body length L in centimeters and the mass M in kilograms of several African Golden cats being studied by a scientist. Determine a power function to model the data.

Power Regression Using the Pwr. Reg tool on a graphing calculator yields y = 0. 018 x 1. 538. The correlation coefficient r for the data, 0. 875, suggests that a power regression accurately reflects the data. Answer: L = 0. 018 M 1. 538

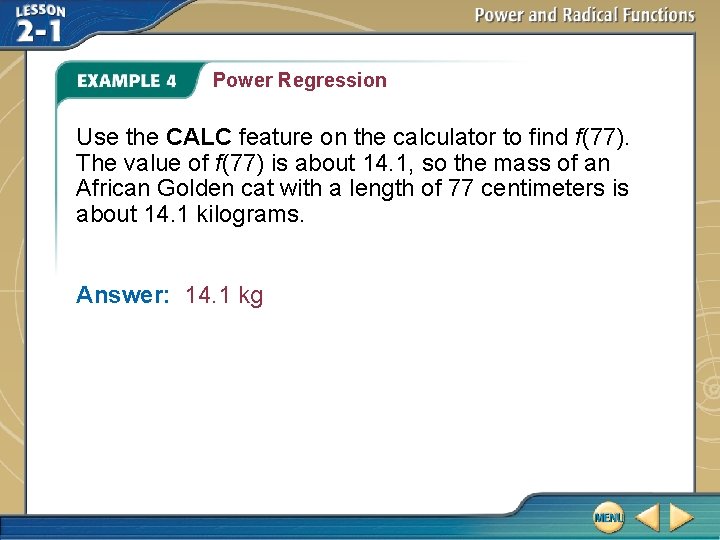
Power Regression C. ANIMALS The following data represent the body length L in centimeters and the mass M in kilograms of several African Golden cats being studied by a scientist. Use the data to predict the mass of an African Golden cat with a length of 77 centimeters.

Power Regression Use the CALC feature on the calculator to find f(77). The value of f(77) is about 14. 1, so the mass of an African Golden cat with a length of 77 centimeters is about 14. 1 kilograms. Answer: 14. 1 kg

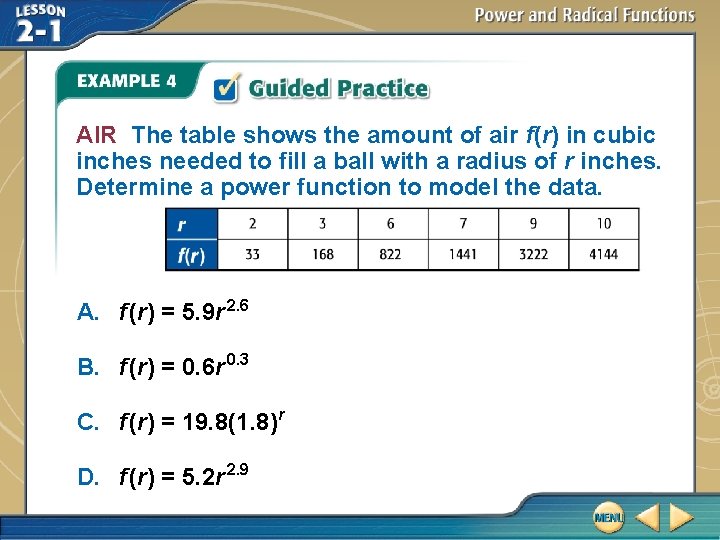
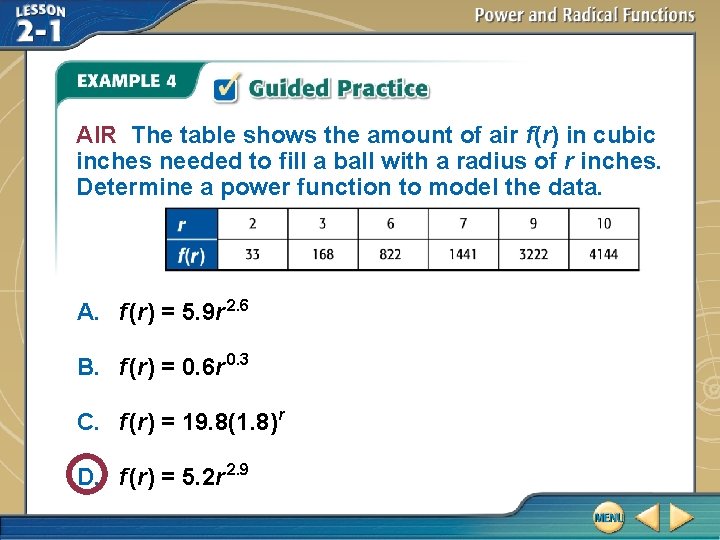
AIR The table shows the amount of air f(r) in cubic inches needed to fill a ball with a radius of r inches. Determine a power function to model the data. A. f (r) = 5. 9 r 2. 6 B. f (r) = 0. 6 r 0. 3 C. f (r) = 19. 8(1. 8)r D. f (r) = 5. 2 r 2. 9

Graph Radical Functions A. Graph and analyze. Describe the domain, range, intercepts, end behavior, continuity, and where the function is increasing or decreasing.

Graph Radical Functions D = [0, ∞); R = [0, ∞); intercept: 0; continuous on [0, ∞); increasing: [0, ∞)

Graph Radical Functions Answer: D = [0, ∞); R = [0, ∞); intercept: 0; ; continuous on [0, ∞); increasing: [0, ∞)

Graph Radical Functions B. Graph and analyze . Describe the domain, range, intercepts, end behavior, continuity, and where the function is increasing or decreasing.

Graph Radical Functions D = (–∞, ∞); R = (–∞, ∞); x-intercept: , y-intercept: about – 0. 6598; ; continuous for all real numbers; increasing: (–∞, ∞)

Graph Radical Functions Answer: D = (–∞, ∞) ; R = (–∞, ∞) ; x-intercept: y-intercept: about – 0. 6598; ; continuous for all real numbers; increasing: (–∞, ∞) ,

Find the intercepts of the graph of A. x-intercept: B. x-intercepts: C. x-intercept: D. x-intercepts: , y-intercept: , y-intercept – 4 .

Solve Radical Equations A. Solve . original equation Isolate the radical. Square each side to eliminate the radical. Subtract 28 x and 29 from each side. Factor. x – 5 = 0 or x + 1 = 0 x =5 x = – 1 Zero Product Property Solve.

Solve Radical Equations Answer: – 1, 5 Check x=5 10 = 10 x = – 1 – 2 = – 2 A check of the solutions in the original equation confirms that the solutions are valid.

Solve Radical Equations B. Solve . original equation Subtract 8 from each side. Raise each side to the third power. (The index is 3. ) Take the square root of each side. x = 10 or – 6 Add 2 to each side. A check of the solutions in the original equation confirms that the solutions are valid. Answer: 10, – 6

Solve Radical Equations C. Solve . original equation Square each side. Isolate the radical. Square each side. (x – 8)(x – 24) = 0 x – 8 = 0 or x – 24 = 0 Distributive Property Combine like terms. Factor. Zero Product Property

Solve Radical Equations x= 8 x = 24 Solve. One solution checks and the other solution does not. Therefore, the solution is 8. Answer: 8

Solve A. 0, 5 B. 11, – 11 C. 11 D. 0, 11 .

• power function • monomial function • radical function • extraneous solution