OUTSTANDING PROBLEMS IN GEOMETRIC CONSTRAINT SOLVING FOR CAD

OUTSTANDING PROBLEMS IN GEOMETRIC CONSTRAINT SOLVING FOR CAD Meera Sitharam, University of Florida Partially supported by NSF grants CCR 99 -02025, EIA 00 -96104

ORGANIZATION n CAD motivation and state of the art n Suite of Formal Problems n Our contribution-- FRONTIER n Unsolved Problems

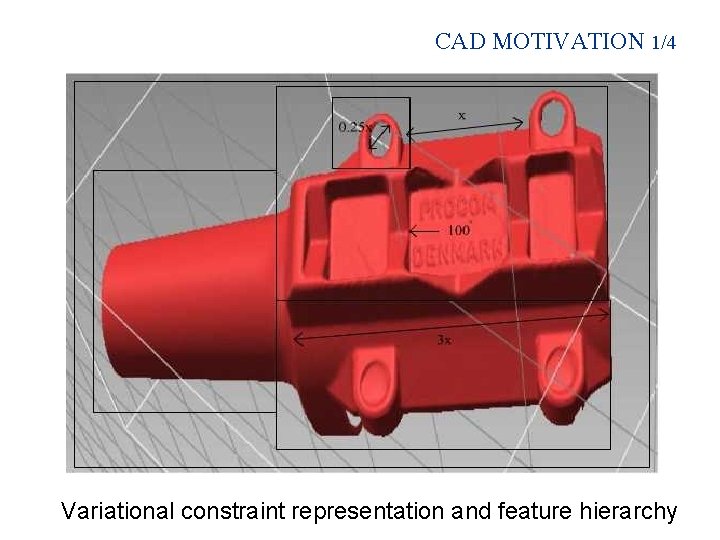
CAD MOTIVATION 1/4 Variational constraint representation and feature hierarchy

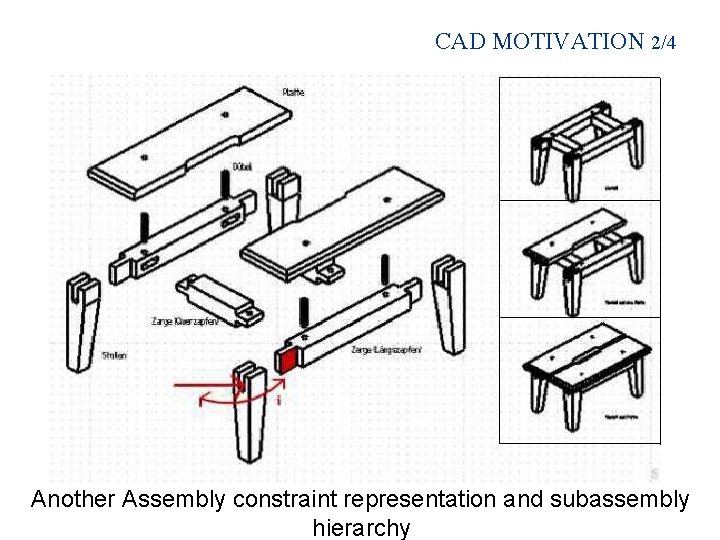
CAD MOTIVATION 2/4 Another Assembly constraint representation and subassembly hierarchy

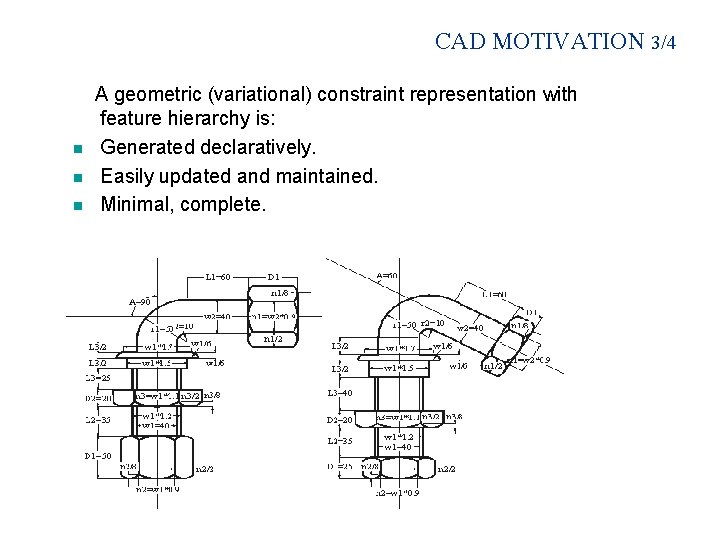
CAD MOTIVATION 3/4 n n n A geometric (variational) constraint representation with feature hierarchy is: Generated declaratively. Easily updated and maintained. Minimal, complete.

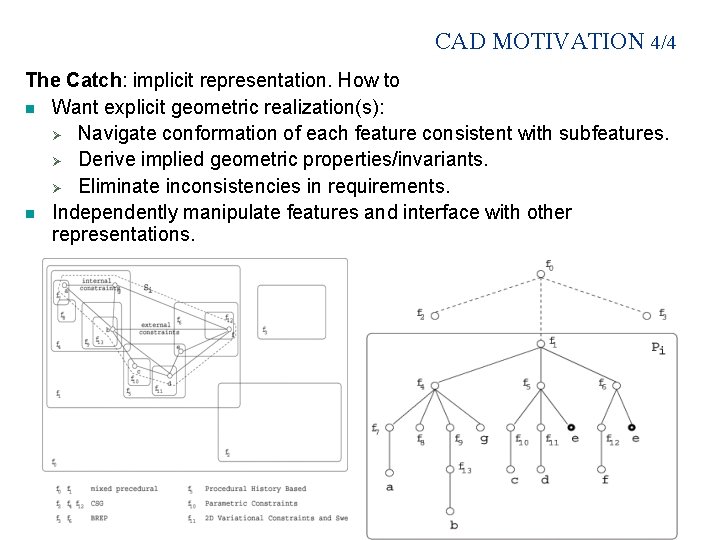
CAD MOTIVATION 4/4 The Catch: implicit representation. How to n Want explicit geometric realization(s): Ø Navigate conformation of each feature consistent with subfeatures. Ø Derive implied geometric properties/invariants. Ø Eliminate inconsistencies in requirements. n Independently manipulate features and interface with other representations.

STATE OF THE ART 1/3 § 2 dimensions : Small, simple, no feature hierarchy, standalone. § 3 dimensions : 2 d views; CSG; history of sweeps, extrusions; parametric constraint solving Hoffman et al (EREP), Bruderlin et al, Bronsvoort et al, Kramer et al, Michelucci et al, Owen et al (D-cubed), Latham, Middleditch et al

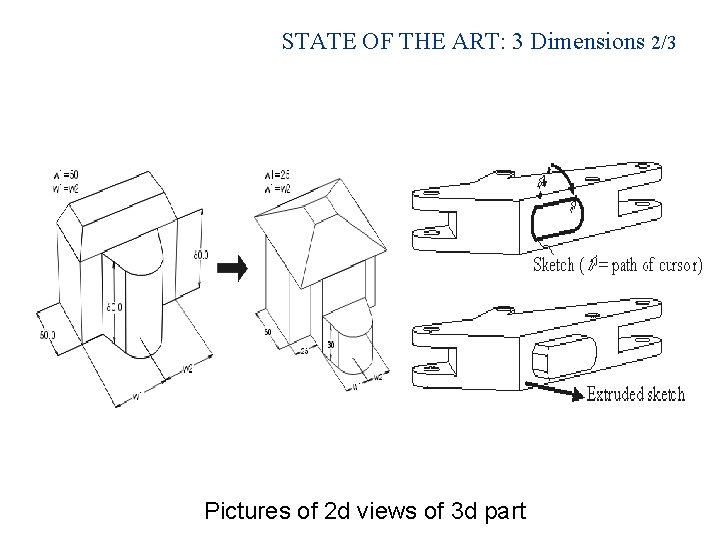
STATE OF THE ART: 3 Dimensions 2/3 Pictures of 2 d views of 3 d part

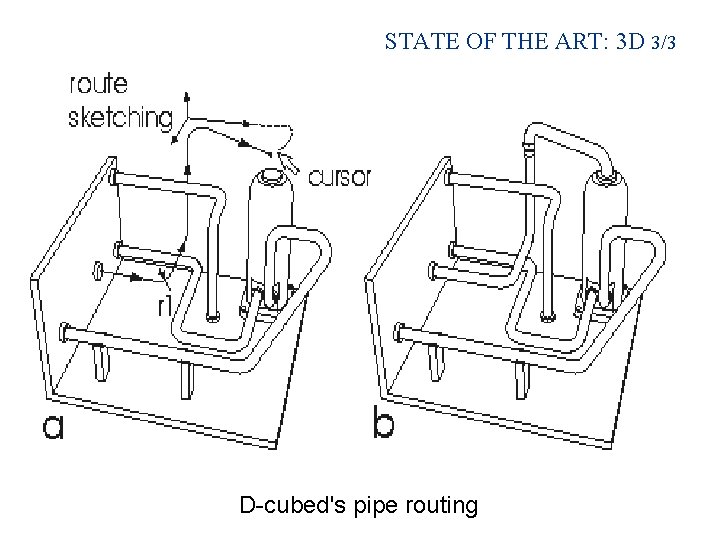
STATE OF THE ART: 3 D 3/3 D-cubed's pipe routing

GOAL

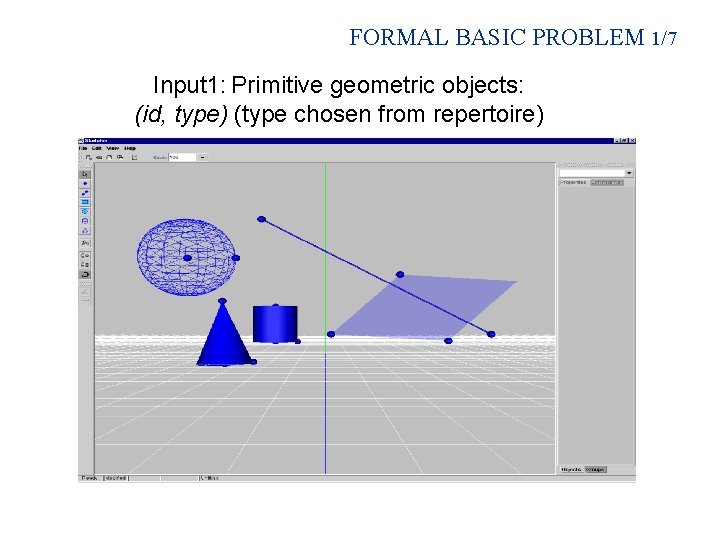
FORMAL BASIC PROBLEM 1/7 Input 1: Primitive geometric objects: (id, type) (type chosen from repertoire)

FORMAL BASIC PROBLEM 2/7 Input 2: Geometric constraints: (object 1, object 2, . . , objectk, type) (type chosen from repertoire) constraint types include some inequalities

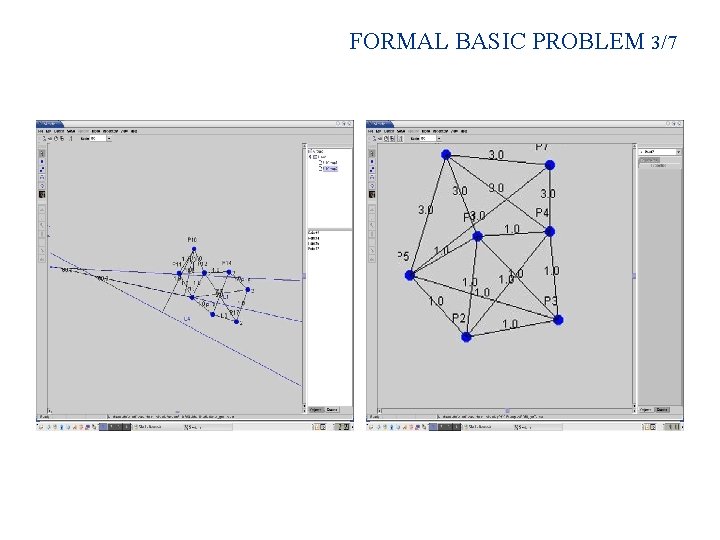
FORMAL BASIC PROBLEM 3/7

FORMAL BASIC PROBLEM 4/7 Input 3 : Feature hierarchies: Ø(more than one) partial order or DAG of subsets of objects Ø partial realization (output) information for the nodes of DAG.

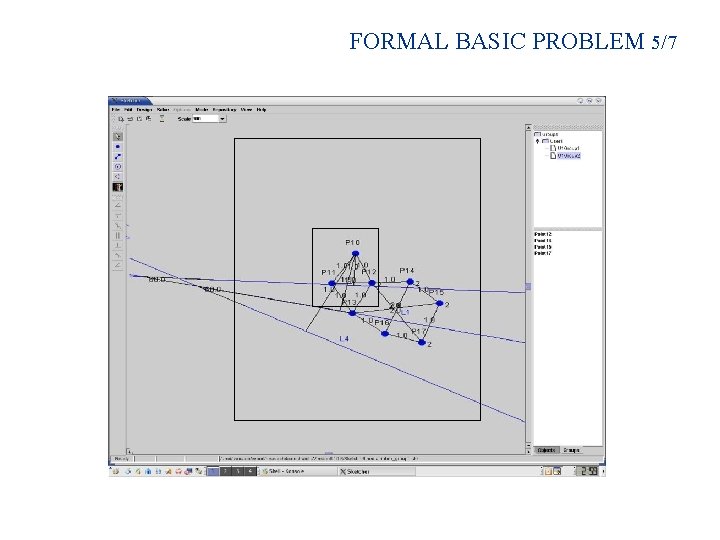
FORMAL BASIC PROBLEM 5/7

FORMAL BASIC PROBLEM 6/7

n n Existence: of realization SUITE OF FORMAL PROBLEMS 1/12 Conformation: One conformation (if it exists) for each node in feature hierarchy, represented as a rigid transformation applied to each child's conformation.

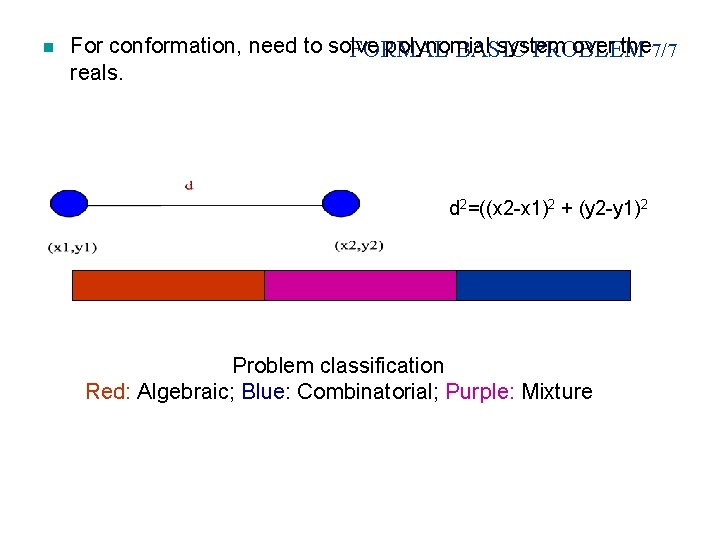
n For conformation, need to solve polynomial system over the 7/7 FORMAL BASIC PROBLEM reals. d 2=((x 2 -x 1)2 + (y 2 -y 1)2 Problem classification Red: Algebraic; Blue: Combinatorial; Purple: Mixture

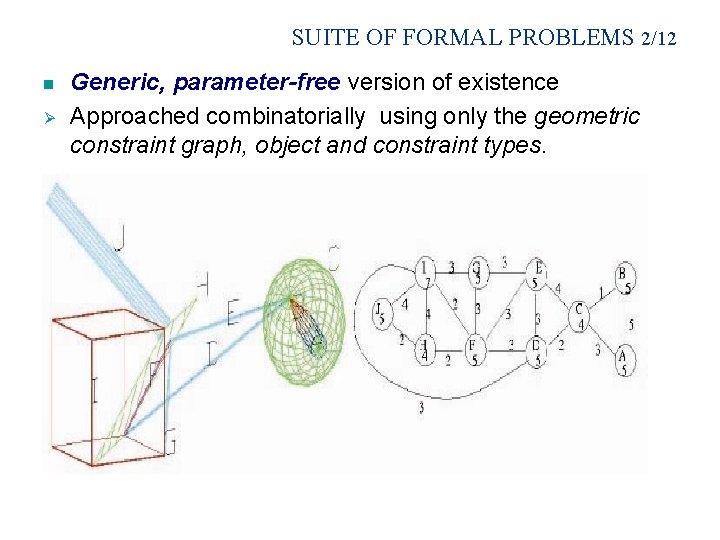
SUITE OF FORMAL PROBLEMS 2/12 n Ø Generic, parameter-free version of existence Approached combinatorially using only the geometric constraint graph, object and constraint types.

SUITE OF FORMAL PROBLEMS 3/12 n Generic answer holds Ø For all but a small set of forbidden parameter values that satisfy discriminant/resultant (in)equalities.

SUITE OF FORMAL PROBLEMS 4/12 n Generic Classification: some information on how many conformations exist? Ø finitely many (rigid or wellconstrained) Ø infinitely many(flexible or underconstrained) Ø none(inconsistently overconstrained)

SUITE OF FORMAL PROBLEMS 5/12 n Navigation: A well-defined set of conformations for each node in feature hierarchy, represented as a set of transformations applied to each child's set of conformations? n Meaning of well-defined: complete in some formal sense, systematically navigable. n Invariant: Does a given geometric property hold for all conformations?

SUITE OF FORMAL PROBLEMS 6/12

SUITE OF FORMAL PROBLEMS 7/12

SUITE OF FORMAL PROBLEMS 8/12

SUITE OF FORMAL PROBLEMS 9/12

SUITE OF FORMAL PROBLEMS 10/12 n Generic Overconstraint correction: a well-defined set of removable constraint-sets for each node in feature hierarchy.

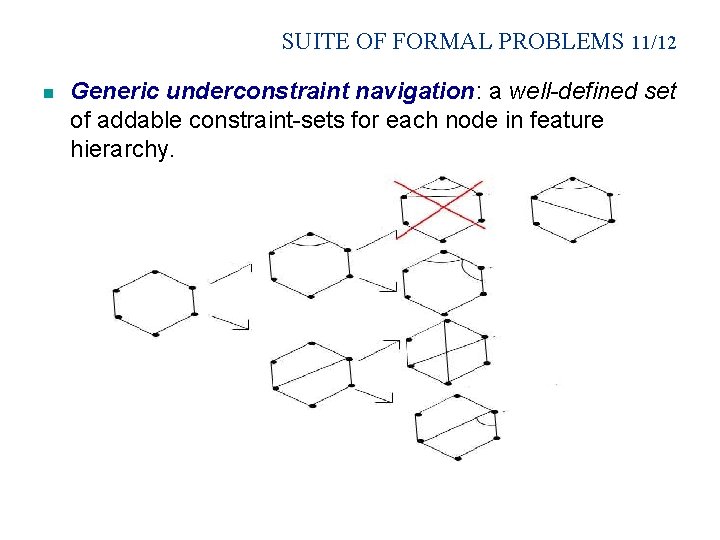
SUITE OF FORMAL PROBLEMS 11/12 n Generic underconstraint navigation: a well-defined set of addable constraint-sets for each node in feature hierarchy.

SUITE OF FORMAL PROBLEMS 12/12 n Combinatorial complete generic solution: Big open question. Gives rise to a combinatorial theory of rigidity. Whiteley et al. n Laman's theorem: complete combinatorial classification for 2 D points and distances. Simple dof analysis.

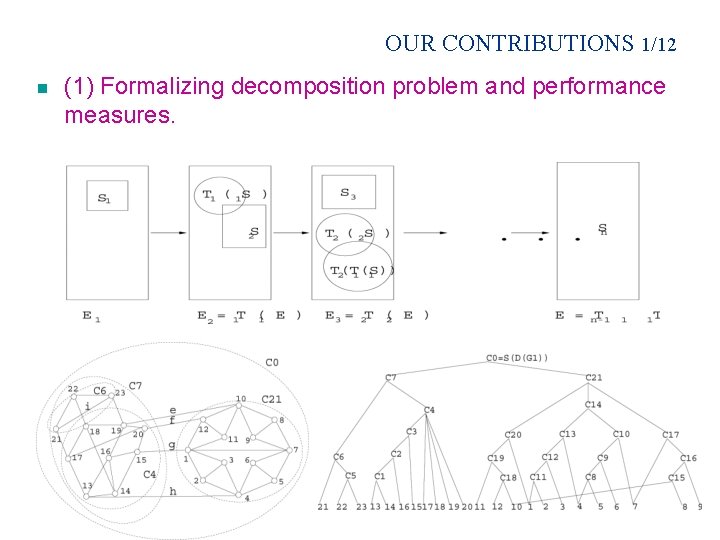
OUR CONTRIBUTIONS 1/12 n (1) Formalizing decomposition problem and performance measures.

OUR CONTRIBUTIONS 2/12 A Decomposition-Recombination plan (DR-plan) for an input constraint system G, consistent with an input feature hierarchy F is a DAG: Ø nodes are subsets of primitive objects of G such that their induced subsystems are well-over-constrained 1 Ø nodes include the nodes of F Ø each leaf/source is a primitive object in S; Ø each root/sink represents a maximal well-over-constrained subsystem of G 1 1 more generally, they possess atmost a specified number of degrees of freedom

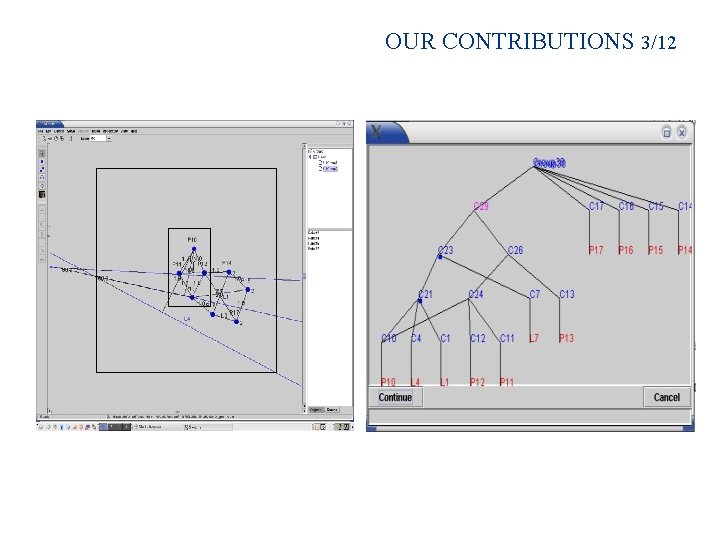
OUR CONTRIBUTIONS 3/12

OUR CONTRIBUTIONS 4/12 Other performance measures on DR-planners ØAn optimal DR-planner minimizes the maximum fan-in (size of the largest subsystem in DR-plan)

OUR CONTRIBUTIONS 5/12 n (2) Partial-generic characterization of DR-plan based on degree of freedom analysis of constraint graphs: minimal dense subgraph usually corresponds to wellover-constrained subsystem. n Algorithm for construction of DR-plan: using network flows to iteratively find the minimal dense subgraphs in current graph transformations that repeatedly simplify them. Ø Ø

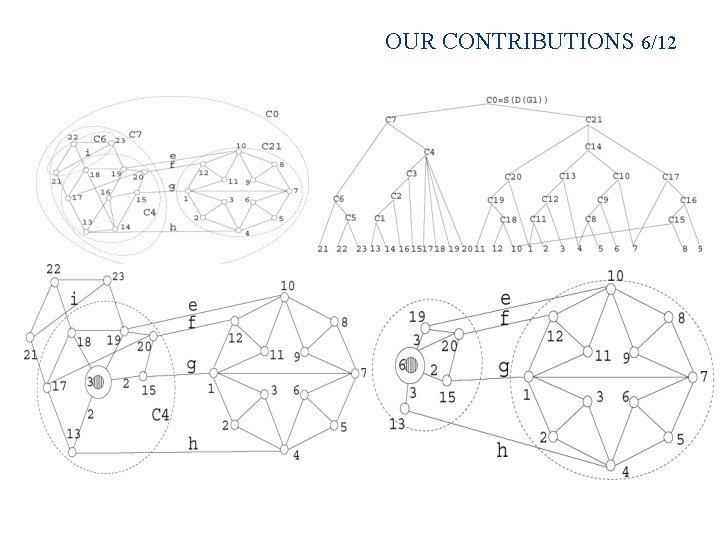
OUR CONTRIBUTIONS 6/12

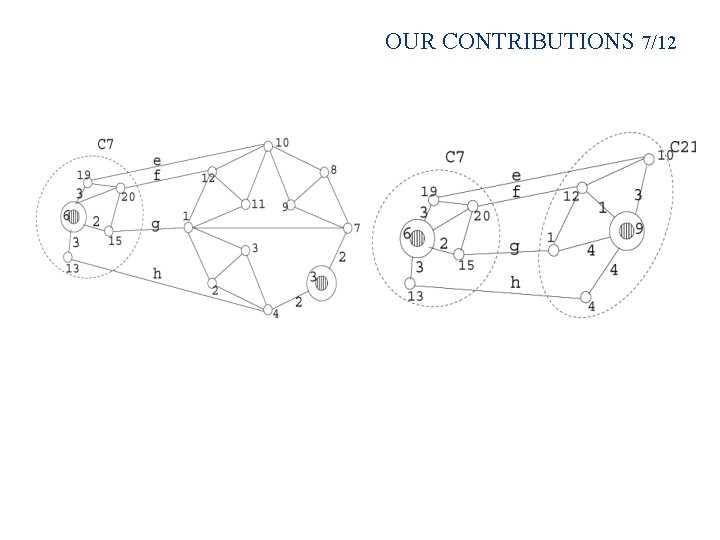
OUR CONTRIBUTIONS 7/12

OUR CONTRIBUTIONS 8/12 Optimal DR Planning problem (Partial-generic version) n. Already finding smallest well-constrained graph is NP-complete. Polynomial time algorithms known for special cases. Approximation status unknown.

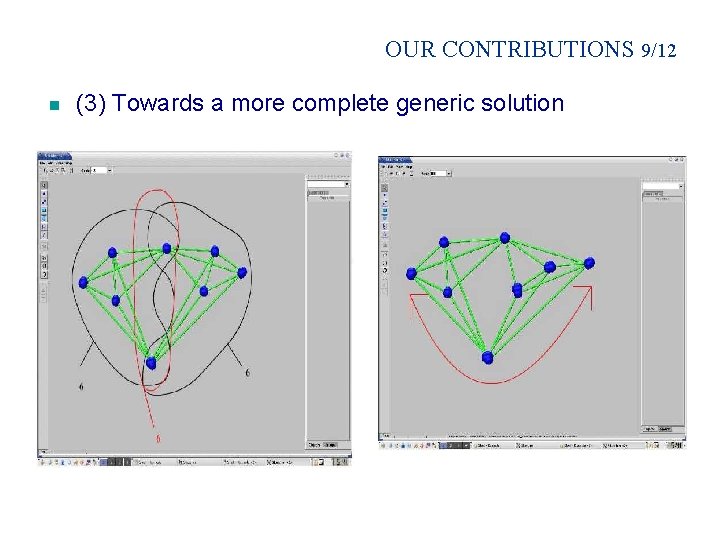
OUR CONTRIBUTIONS 9/12 n (3) Towards a more complete generic solution

OUR CONTRIBUTIONS 10/12

OUR CONTRIBUTIONS 11/12 n Ø Ø Ø Ø Ø (4) Decomposition gives partial-generic solution to: Existence Classification Overconstraint Correction Generic underconstraint Navigation Dealing with mixed representations, multiple input feature hierarchies (5) Plus additional work on equation and conformation management gives: Well-constrained Conformations Well-constrained Navigation Easy updates of constraint repertoire Easy updates of constraint representation, feature hierarchy and realizations Online constraint solving

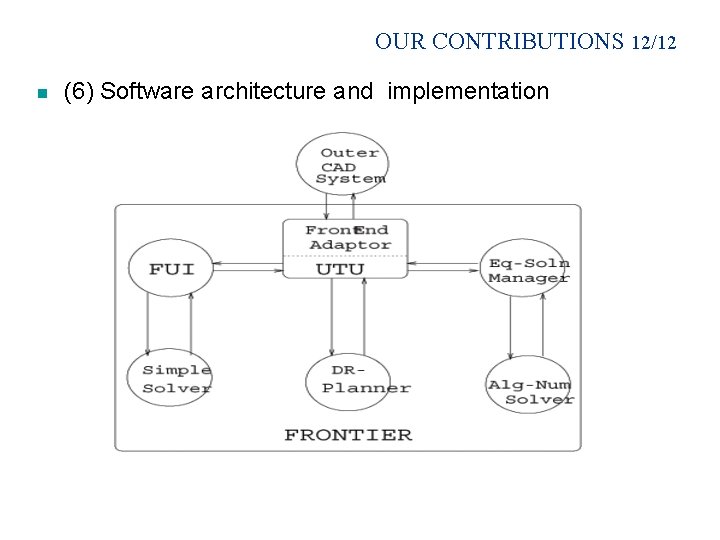
OUR CONTRIBUTIONS 12/12 n (6) Software architecture and implementation

REITERATING UNSOLVED PROBLEMS 1/3 n Isolation of Conformation: Chirality, Semi-global constraints, Symmetries, Forces. n Efficiently solving polynomial systems for rigid transformations : physically based semi-numerical algorithms are welcome. n Invariant problem. n Inverse problem of finding minimal constraint representation

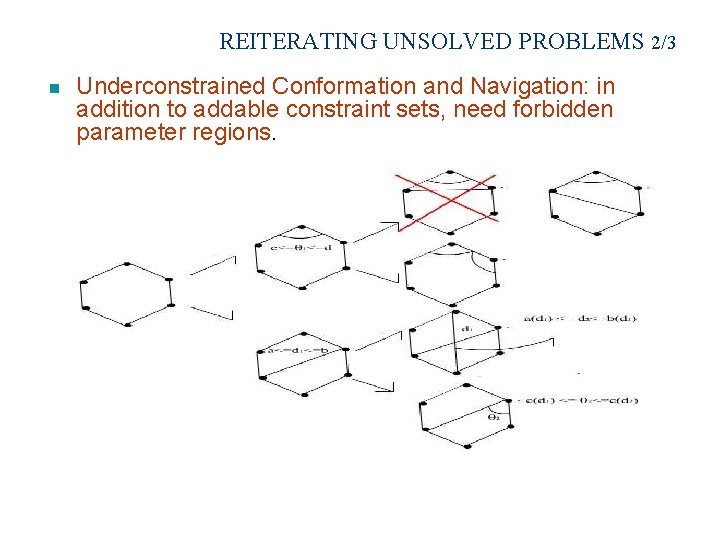
REITERATING UNSOLVED PROBLEMS 2/3 n Underconstrained Conformation and Navigation: in addition to addable constraint sets, need forbidden parameter regions.

REITERATING UNSOLVED PROBLEMS 3/3 n Complete generic solution to original problems-combinatorial geometry, geometric graphs. n Approximation algorithm for Optimal DR-plan problem, even the partial-generic version based on dof analysis. n Complexity of existence problem NP-hard; not known to be in NP; in DNPR (partial algebraic version of NP); not known to be DNPR-hard. n Algebraic description of generic describe the semialgebraic set of forbidden parameter values when generic solution does not hold