OUTPUT INPUT STABILITY Daniel Liberzon Coordinated Science Laboratory

OUTPUT – INPUT STABILITY Daniel Liberzon Coordinated Science Laboratory and Dept. of Electrical & Computer Eng. , Univ. of Illinois at Urbana-Champaign MTNS ’ 02

MOTIVATION ISS: stability (no outputs) detectability (no inputs) minimum phase s linear: stable eigenvalues linear: stable unobserv. modes linear: stable zeros stable inverse ? ? ?

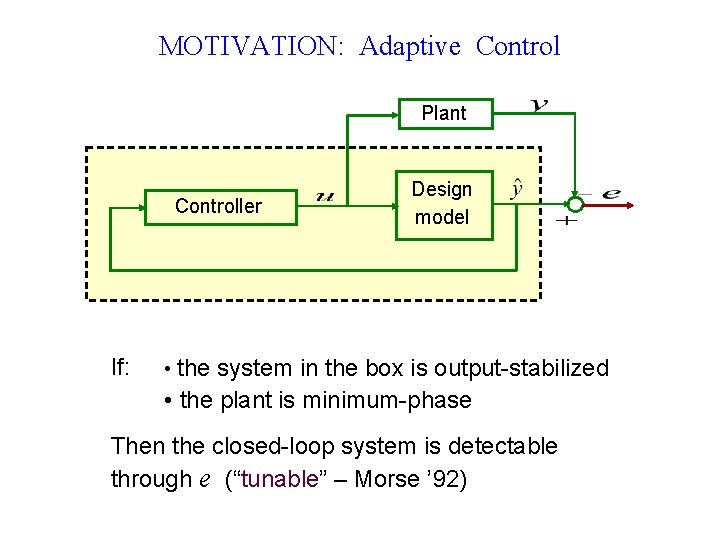
MOTIVATION: Adaptive Control Plant Controller If: Design model • the system in the box is output-stabilized • the plant is minimum-phase Then the closed-loop system is detectable through e (“tunable” – Morse ’ 92)

DEFINITION Call the system output-input stable if s. t. where Example: integer N and functions

UNDERSTANDING OUTPUT-INPUT STABILITY 1 Output-input stability: 2 Uniform detectability w. r. t. extended output: 3 Input-bounding property: 1 <=> 2 + 3

SISO SYSTEMS For systems analytic in controls, can replace the input-bounding property by where is the first derivative containing u For affine systems: this reduces to relative degree ( ) doesn’t have this property For affine systems in global normal form, output-input stability ISS internal dynamics

MIMO SYSTEMS Existence of relative degree no longer necessary For linear systems reduces to usual minimum phase notion Input-bounding property – via Hirschorn’s algorithm Example: Extensions: Singh’s algorithm, non-affine systems

INPUT / OUTPUT OPERATORS Operator is output-input stable if A system is output-input stable if and only if its I/O mapping (for zero i. c. ) is output-input stable under suitable minimality assumptions

APPLICATION: FEEDBACK DESIGN Output stabilization state stabilization Example: ( r – relative degree) Apply u to have with A stable Output-input stability guarantees closed-loop GAS No global normal form is needed

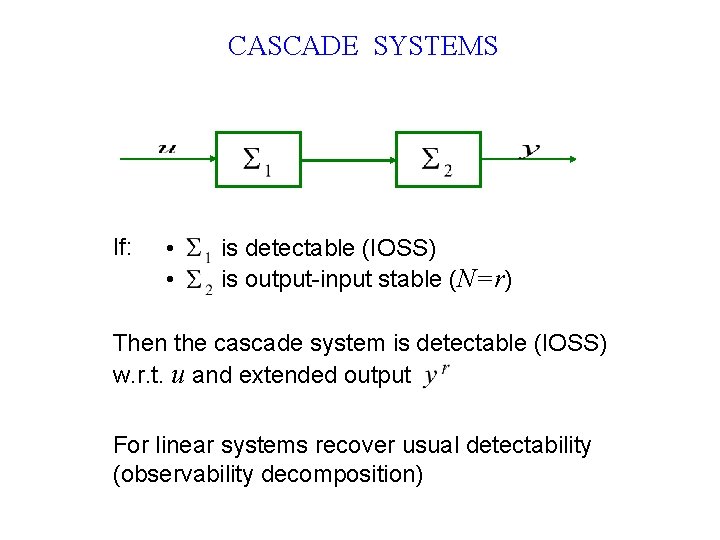
CASCADE SYSTEMS If: • • is detectable (IOSS) is output-input stable (N=r) Then the cascade system is detectable (IOSS) w. r. t. u and extended output For linear systems recover usual detectability (observability decomposition)

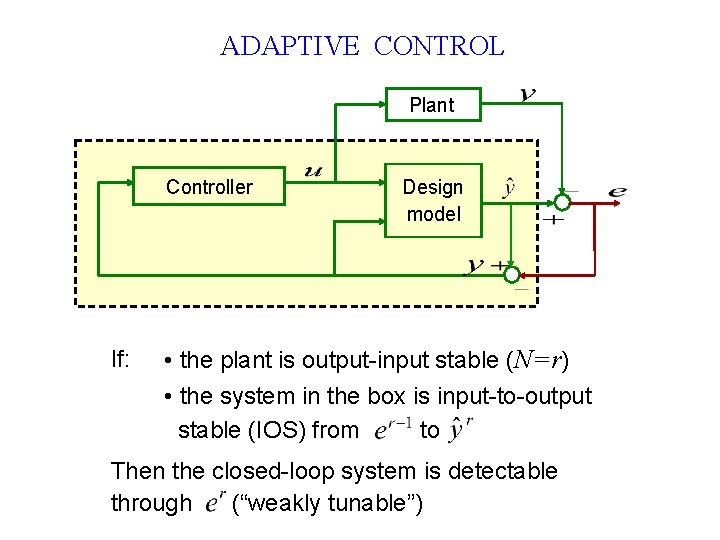
ADAPTIVE CONTROL Plant Controller If: Design model • the plant is output-input stable (N=r) • the system in the box is input-to-output stable (IOS) from to Then the closed-loop system is detectable through (“weakly tunable”)

SUMMARY New notion of output-input stability § applies to general smooth nonlinear control systems § reduces to minimum phase for linear (MIMO) systems § robust variant of Byrnes-Isidori minimum phase notion § relates to ISS, detectability, left-invertibility § extends to input/output operators Applications: § Feedback stabilization § Cascade connections § Adaptive control § More ?