Outline Theoretical Foundations Fundamental limitations of distributed systems

Outline • Theoretical Foundations – Fundamental limitations of distributed systems – Logical clocks 12/27/2021 COP 5611 1

Distributed Systems • A distributed system is a collection of independent computers that appears to its users as a single coherent system – Independent computers mean that they do not share memory or clock – The computers communicate with each other by exchanging messages over a communication network • The messages are delivered after an arbitrary transmission delay 12/27/2021 COP 5611 2

Inherent Limitations of a Distributed System • Absence of a global clock – In a centralized system, time is unambiguous – In a distributed system, there exists no system wide common clock • In other words, the notion of global time does not exist – Impact of the absence of global time • Difficult to reason about temporal order of events • Makes it harder to collect up-to-date information on the state of the entire system 12/27/2021 COP 5611 3

Absence of Global Time • When each machine has its own clock, an event that occurred after another event may nevertheless be assigned an earlier time. 12/27/2021 COP 5611 4

Inherent Limitations of a Distributed System • Absence of shared memory – An up-to-date state of the entire system is not available to any individual process • This information, however, is necessary to reason about the system’s behavior, debugging, recovering from failures 12/27/2021 COP 5611 5

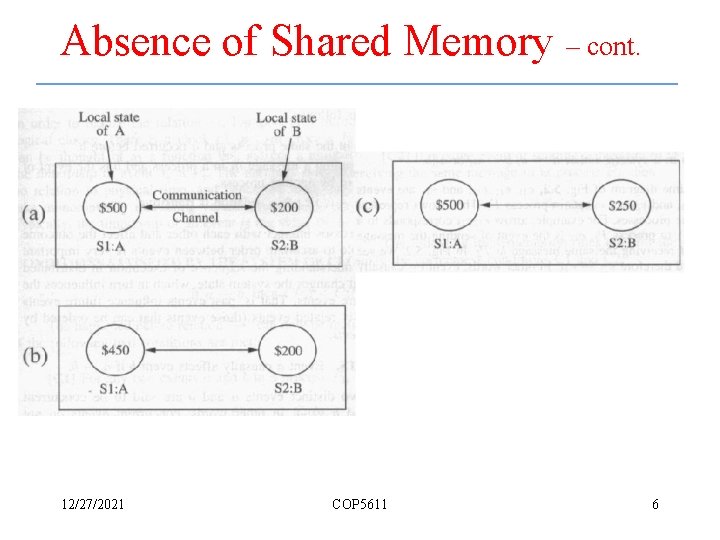
Absence of Shared Memory – cont. 12/27/2021 COP 5611 6

Two Approaches for a Global Clock • First approach is to physically synchronize the clocks on different computers – Synchronize them to a common server – Synchronize them to an average of the clocks • Second approach is to establish what is known as logical clock – They can be used to reason about the temporal ordering of events – But they are not related to the physical clock 12/27/2021 COP 5611 7

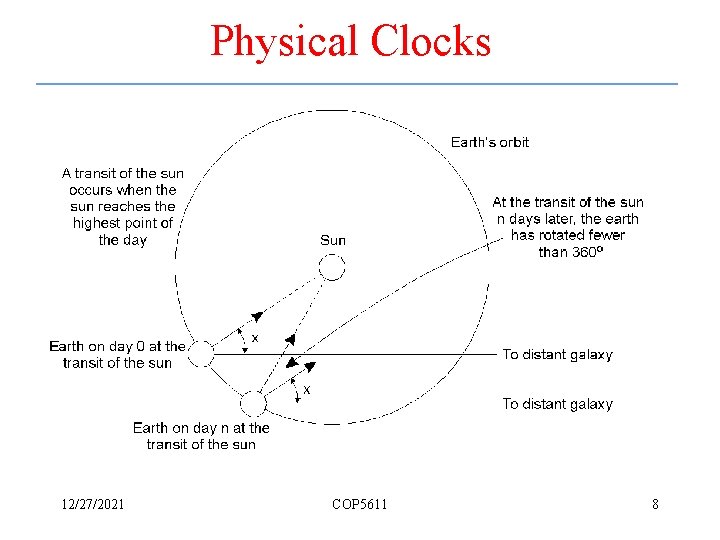
Physical Clocks 12/27/2021 COP 5611 8

Physical Clocks – cont. • TAI seconds are of constant length, unlike solar seconds. Leap seconds are introduced when necessary to keep in phase with the sun. 12/27/2021 COP 5611 9

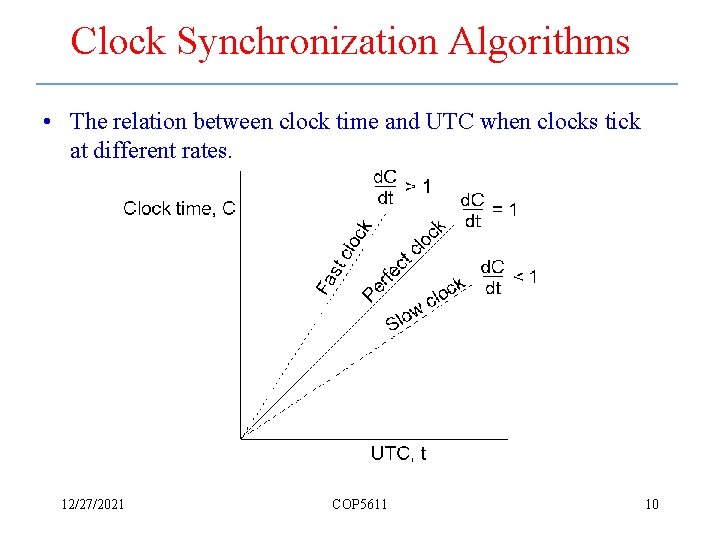
Clock Synchronization Algorithms • The relation between clock time and UTC when clocks tick at different rates. 12/27/2021 COP 5611 10

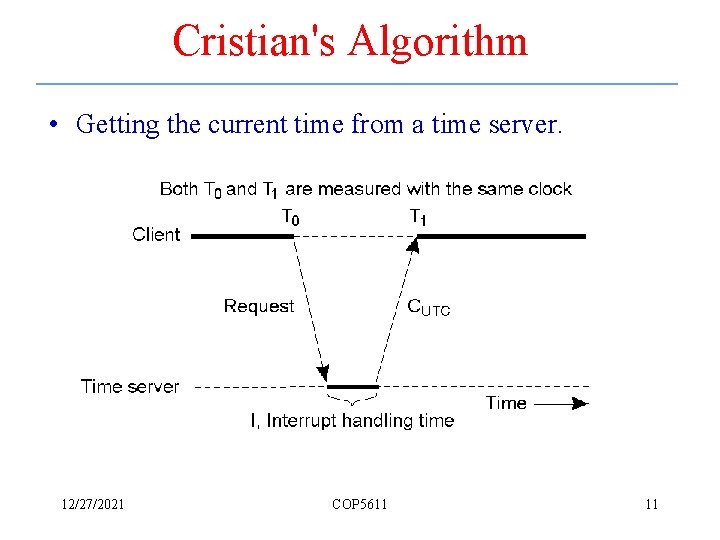
Cristian's Algorithm • Getting the current time from a time server. 12/27/2021 COP 5611 11

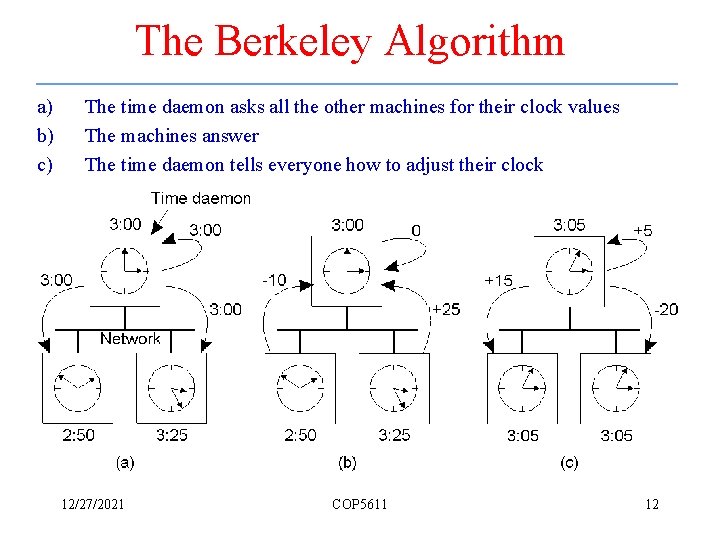
The Berkeley Algorithm a) b) c) The time daemon asks all the other machines for their clock values The machines answer The time daemon tells everyone how to adjust their clock 12/27/2021 COP 5611 12

Logical Clocks • There are technical issues with the clock synchronization approaches – Due to unpredictable message transmission delays, two processes can observe a global clock value at different instants – The physical clocks can drift from the physical time and thus we cannot have a system of perfectly synchronized clocks • For many purposes, it is sufficient that all machines agree on the same time 12/27/2021 COP 5611 13

Lamport’s Logical Clocks • Logical clocks – For a wide of algorithms, what matters is the internal consistency of clocks, not whether they are close to the real time – For these algorithms, the clocks are often called logical locks • Lamport proposed a scheme to order events in a distributed system using logical clocks 12/27/2021 COP 5611 14

Lamport’s Logical Clocks – cont. • Definitions – Happened before relation • Happened before relation ( ) captures the causal dependencies between events • It is defined as follows – a b, if a and b are events in the same process and a occurred before b. – a b, if a is the event of sending a message m in a process and b is the event of receipt of the same message m by another process – If a b and b c, then a c, i. e. , “ ” is transitive 12/27/2021 COP 5611 15

Lamport’s Logical Clocks – cont. • Definitions – continued – Causally related events • Event a causally affects event b if a b – Concurrent events • Two distinct events a and b are said to be concurrent (denoted by a || b) if a b and b a • For any two events, either a b, b a, or a || b 12/27/2021 COP 5611 16

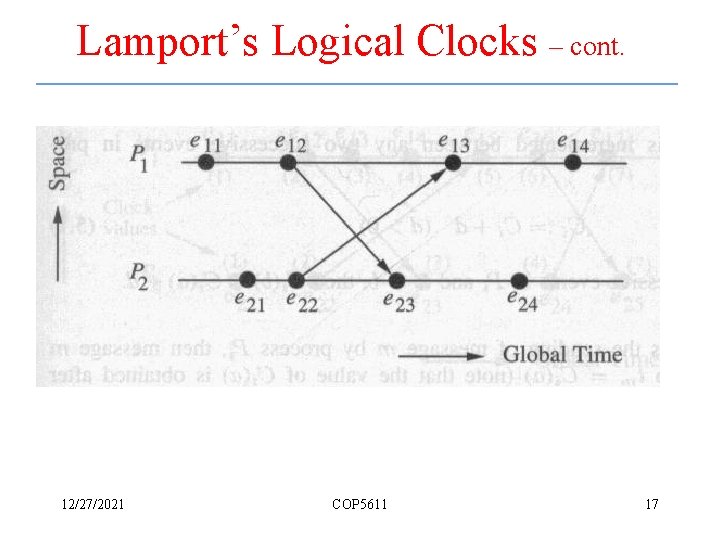
Lamport’s Logical Clocks – cont. 12/27/2021 COP 5611 17

Lamport’s Logical Clocks – cont. • Logical clocks – There is a clock at each process Pi in the system • Which is a function that assigns a number to any event a, called the timestamp of event a at Pi • The numbers assigned by the system of the clocks have no relation to physical time • The logical clocks take monotonically increasing values and can be implemented as counters 12/27/2021 COP 5611 18

Lamport’s Logical Clocks – cont. • Conditions satisfied by the system of clocks – For any two events, if a b, then C(a) < C(b) – [C 1] For any two events a and b in a process Pi, if a occurs before b, then Ci(a) < Ci(b) – [C 2] If a is the event of sending a message m in process Pi and b is the event of receiving the same message m at process Pj, then Ci(a) < Cj(b) 12/27/2021 COP 5611 19

Lamport’s Logical Clocks – cont. • Implementation rules – [IR 1] Clock Ci is incremented between any two successive events in process Pi Ci : = Ci + d ( d > 0) – [IR 2] If event a is the sending of message m by process Pi, then message m is assigned a timestamp tm = Ci(a). On receiving the same message m by process Pj, Cj is set to Cj : = max(Cj, tm + d) 12/27/2021 COP 5611 20

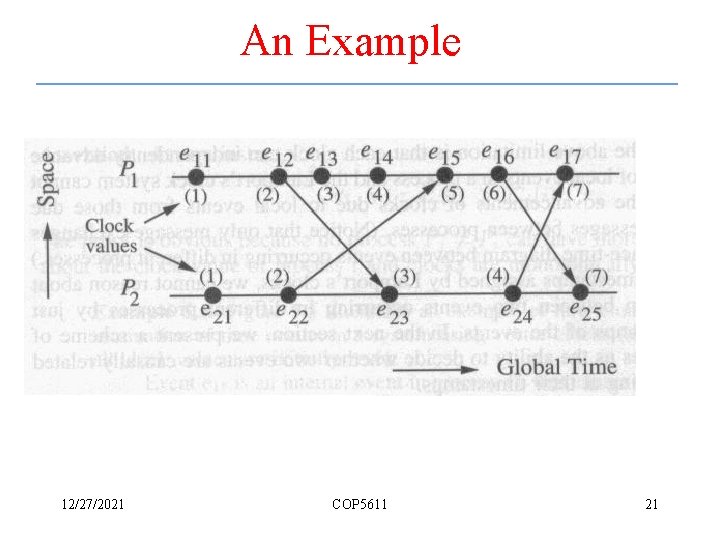
An Example 12/27/2021 COP 5611 21

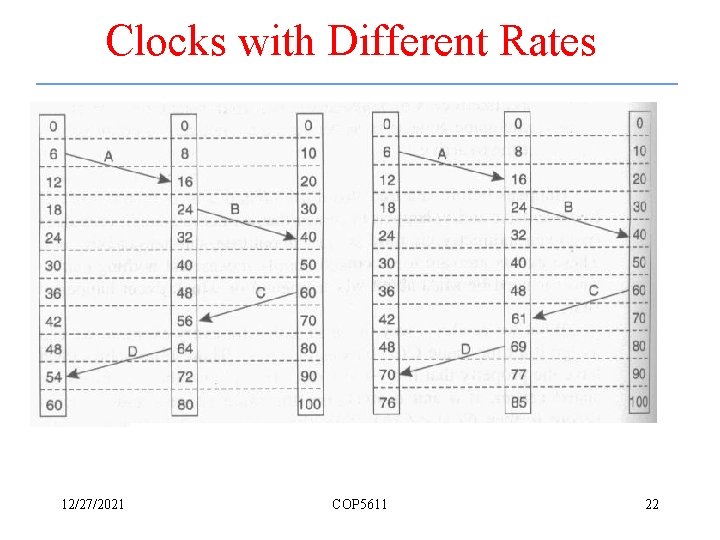
Clocks with Different Rates 12/27/2021 COP 5611 22

Total Ordering Using Lamport’s Clocks • If a is any event at process Pi and b is any event at process Pj, then a => b if and only if either – Where is any arbitrary relation that totally orders the processes to break ties 12/27/2021 COP 5611 23

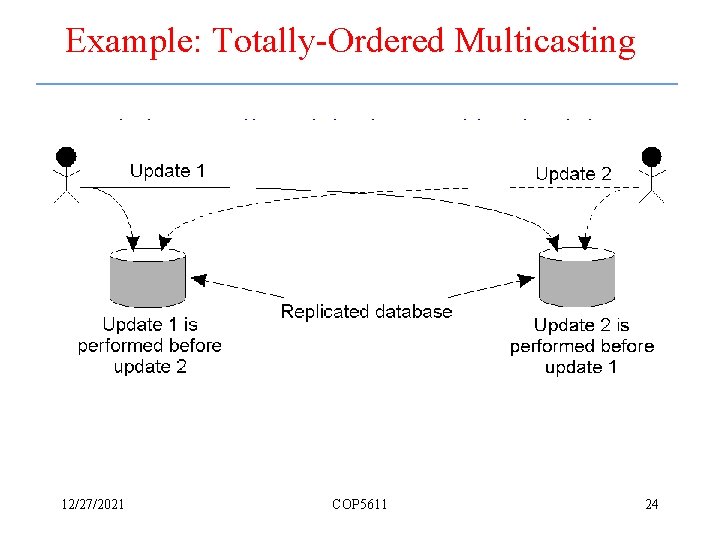
Example: Totally-Ordered Multicasting • Updating a replicated database and leaving it in an inconsistent state. 12/27/2021 COP 5611 24

A Limitation of Lamport’s Clocks • In Lamport’s system of logical clocks – If a b, then C(a) < C(b) – The reverse if not necessarily true if the events have occurred on different processes 12/27/2021 COP 5611 25

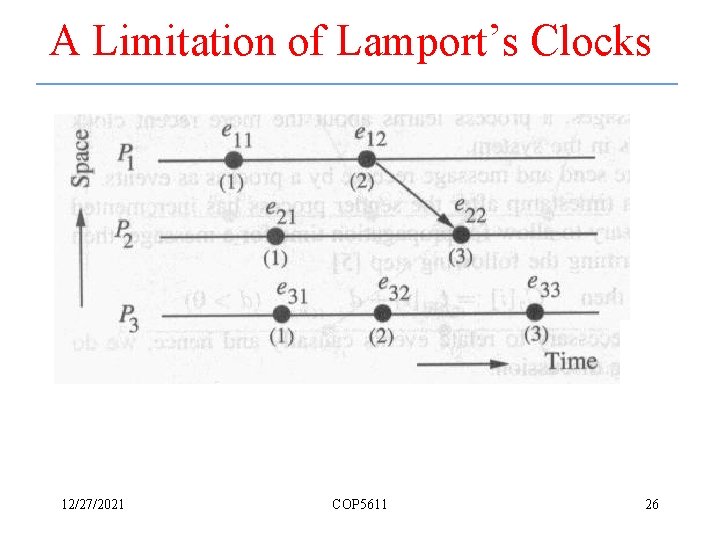
A Limitation of Lamport’s Clocks 12/27/2021 COP 5611 26

Vector Clocks • Implementation rules – [IR 1] Clock Ci is incremented between any two successive events in process Pi Ci[i] : = Ci[i] + d ( d > 0) – [IR 2] If event a is the sending of message m by process Pi, then message m is assigned a timestamp tm = Ci(a). On receiving the same message m by process Pj, Cj is set to Cj[k] : = max(Cj[k], tm[k]) 12/27/2021 COP 5611 27

Vector Clocks – cont. 12/27/2021 COP 5611 28

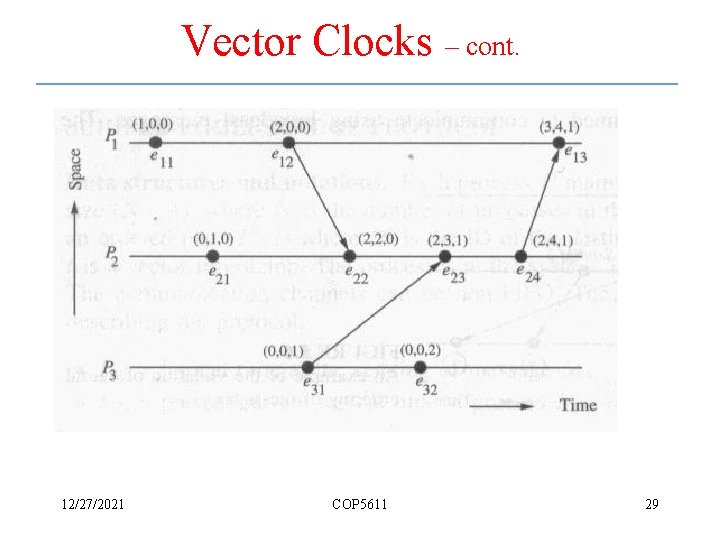
Vector Clocks – cont. 12/27/2021 COP 5611 29

Vector Clocks – cont. • Assertion – At any instant, • Events a and b are casually related if ta < tb or tb < ta. Otherwise, these events are concurrent • In a system of vector clocks, 12/27/2021 COP 5611 30