Outline Theoretical Foundations continued Lab 1 Lamports algorithm

Outline • Theoretical Foundations - continued – Lab 1 • Lamport’s algorithm for distributed mutual exclusion – Casual ordering of messages – continued – Global state – Cuts – Termination detection 10/24/2021 COP 5611 1

Regarding Lab 1 • For this project, you can work as a team with at most two members per team – Each team only needs to turn in one report – However, all the members are required to understand all the parts as you may be tested on the midterm or the final exam • Three processes – Bank Account Server – Bank Office Clients – Bank Office Mutual Exclusion Processes 10/24/2021 COP 5611 2
![Lamport’s Clock • Implementation rules – [IR 1] Clock Ci is incremented between any Lamport’s Clock • Implementation rules – [IR 1] Clock Ci is incremented between any](http://slidetodoc.com/presentation_image_h2/e74a7bbb6f704b027a392d791e2ddeef/image-3.jpg)
Lamport’s Clock • Implementation rules – [IR 1] Clock Ci is incremented between any two successive events in process Pi Ci : = Ci + d ( d > 0) – [IR 2] If event a is the sending of message m by process Pi, then message m is assigned a timestamp tm = Ci(a). On receiving the same message m by process Pj, Cj is set to Cj : = max(Cj, tm + d) 10/24/2021 COP 5611 3

Total Ordering Using Lamport’s Clocks • If a is any event at process Pi and b is any event at process Pj, then a => b if and only if either – Where is any arbitrary relation that totally orders the processes to break ties 10/24/2021 COP 5611 4

Lamport’s Distributed Mutual Exclusion Algorithm • This algorithm is based on the total ordering using Lamport’s clocks – Each process keeps a Lamport’s logical clock • Each process is associated with a unique id that can be used to break the ties – In the algorithm, each process keeps a queue, request_queuei, which contains mutual exclusion requests ordered by their timestamp and associated id – Ri of each process consists of all the processes – The communication channel is assumed to be FIFO 10/24/2021 COP 5611 5

Lamport’s Distributed Mutual Exclusion Algorithm – cont. 10/24/2021 COP 5611 6

Lamport’s Distributed Mutual Exclusion Algorithm – cont. 10/24/2021 COP 5611 7
![Vector Clocks • Implementation rules – [IR 1] Clock Ci is incremented between any Vector Clocks • Implementation rules – [IR 1] Clock Ci is incremented between any](http://slidetodoc.com/presentation_image_h2/e74a7bbb6f704b027a392d791e2ddeef/image-8.jpg)
Vector Clocks • Implementation rules – [IR 1] Clock Ci is incremented between any two successive events in process Pi Ci[i] : = Ci[i] + d ( d > 0) – [IR 2] If event a is the sending of message m by process Pi, then message m is assigned a timestamp tm = Ci(a). On receiving the same message m by process Pj, Cj is set to Cj[k] : = max(Cj[k], tm[k]) 10/24/2021 COP 5611 8

Vector Clocks – cont. • In a system of vector clocks, where 10/24/2021 COP 5611 9

Causal Ordering of Messages • The causal ordering of messages tries to maintain the same causal relationship that holds among “message send” events with the corresponding “message receive” events – In other words, if Send(M 1) -> Send(M 2), then Receive(M 1) -> Receive(M 2) – This is different from causal ordering of events 10/24/2021 COP 5611 10

Birman-Schiper-Stephenson Protocol 10/24/2021 COP 5611 11

Schiper-Eggli-Sando Protocol 10/24/2021 COP 5611 12

Schiper-Eggli-Sando Protocol – cont. 10/24/2021 COP 5611 13

Schiper-Eggli-Sando Protocol – cont. 10/24/2021 COP 5611 14
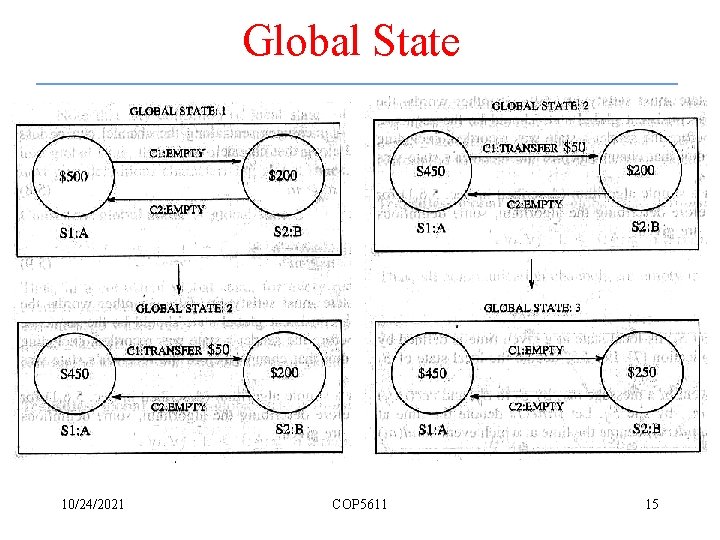
Global State 10/24/2021 COP 5611 15

Local State • Local state – For a site Si, its local state at a given time is defined by the local context of the distributed application, denoted by LSi. • More notations – mij denotes a message sent by Si to Sj – send(mij) and rec(mij) denote the corresponding sending and receiving event. 10/24/2021 COP 5611 16

Definitions – cont. 10/24/2021 COP 5611 17

Definitions – cont. 10/24/2021 COP 5611 18
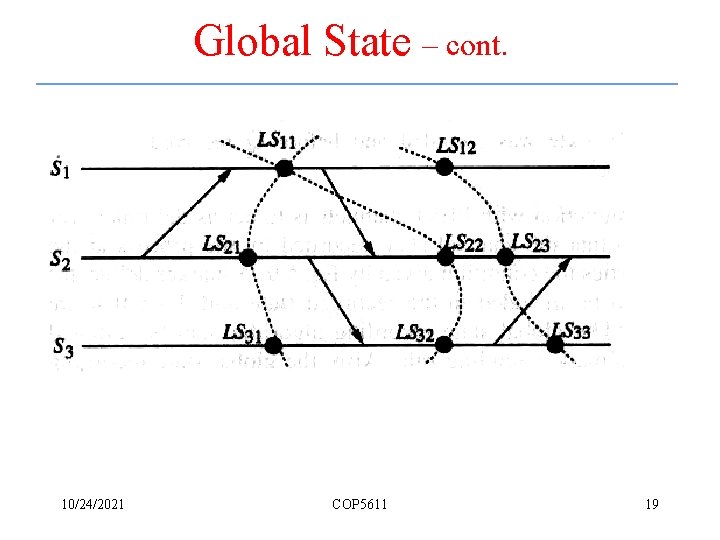
Global State – cont. 10/24/2021 COP 5611 19

Definitions – cont. Strongly consistent global state: A global state is strongly consistent if it is consistent and transitless 10/24/2021 COP 5611 20
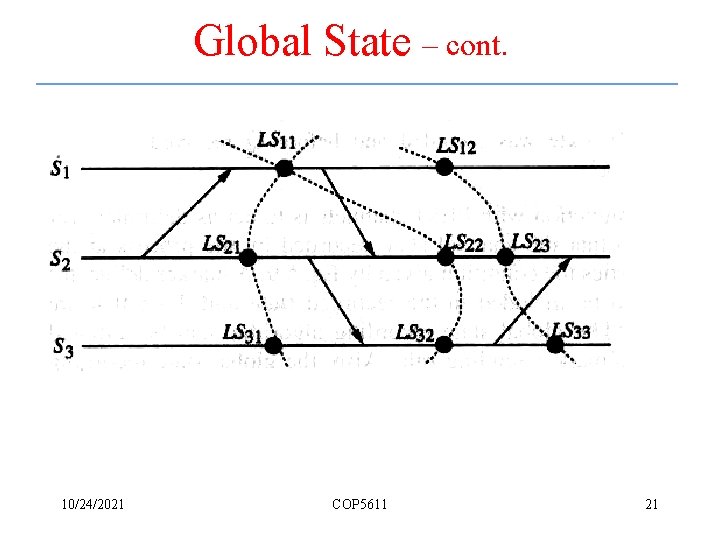
Global State – cont. 10/24/2021 COP 5611 21

Chandy-Lamport’s Global State Recording Algorithm 10/24/2021 COP 5611 22

Cuts of a Distributed Computation • A cut is a graphical representation of a global state – A consistent cut is a graphical representation of a consistent global state • Definition – A cut of a distributed computation is a set C={c 1, c 2, . . , cn}, where ci is a cut event at site Si in the history of the distributed computation 10/24/2021 COP 5611 23

Cuts of a Distributed Computation – cont. 10/24/2021 COP 5611 24

Cuts of a Distributed Computation – cont. 10/24/2021 COP 5611 25

Cuts of a Distributed Computation – cont. 10/24/2021 COP 5611 26

Cuts of a Distributed Computation – cont. 10/24/2021 COP 5611 27

Cuts of a Distributed Computation – cont. 10/24/2021 COP 5611 28

Termination Detection • Termination detection is to detect when a distributed algorithm is terminated, such as election, a deadlock detection, or token generating algorithm – A process can be active or idle – A computation is said to have terminated if and only if all the processes are idle and there are no messages in transit – Basic idea • We are not going to cover the algorithm in detail 10/24/2021 COP 5611 29

Summary • The absence of global time and the absence of shared memory are two main characteristics of distributed systems – Two schemes, Lamport’s logical clocks and vector clocks are used to order events – Two algorithms for causal ordering of messages based on the vector clock-based ideas are discussed – Global states and cuts of a distributed system are also covered – These provide theoretical foundations for other distributed algorithms 10/24/2021 COP 5611 30
- Slides: 30