Outline secrets equivalence between row operations matrix multiplication

Outline è secrets è equivalence between row operations & matrix multiplication è simplex è revised tableau in matrix form simplex method èrelationship with column generation 1

The Most Beautiful … 2

Maybe the Most Beautiful of All… è linear algebra geometric properties algebraic properties matrix properties 3

To be at Home with the Material è familiar è be with the equivalence lazy èkeeping èe. g. , and working only with the essence how much information to carry in solving è (sometimes) èe. g. , use logic, not eyes in some sense 4

Equivalence Between Row Operations & Matrix Multiplication w x y (1) b making w basic in (1) row operations: (a) (1 ) = (1)/3 (b) (2 ) = (2)-2(1 ) (2) è let E= è EA (1 ) (2 ) and A = = 5

Equivalence Between Row Operations & Matrix Multiplication w x y b (1) making y basic in (2) (1 ) (2) row operations: (a) (2 ) = (2)/4 (b) (1 ) = (1)+8(2 ) è let E= è EA and A = = 6

Equivalence Between Row Operations & Matrix Multiplication è what v should E be to make “v basic in (3)”? w x y b 7

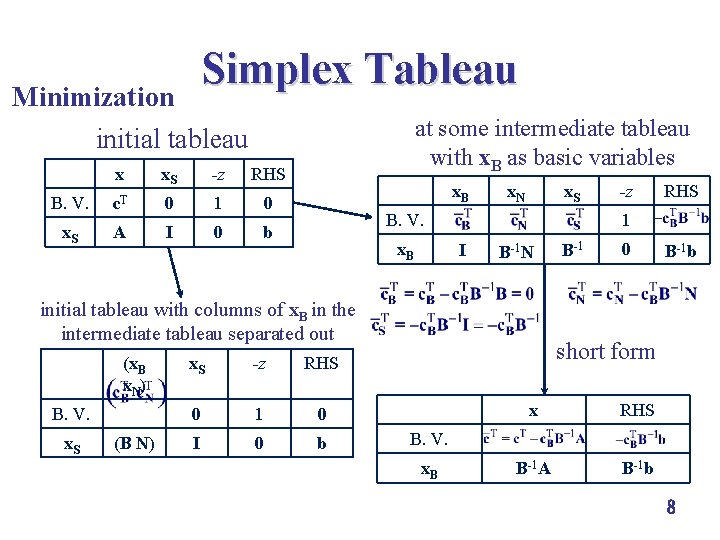
Simplex Tableau Minimization initial tableau x x. S -z RHS B. V. c. T 0 1 0 x. S A I 0 b at some intermediate tableau with x. B as basic variables x. B x. N x. S B. V. x. B B. V. x. S (B N) x. S -z RHS 0 1 0 I 0 b RHS 1 I B-1 N initial tableau with columns of x. B in the intermediate tableau separated out (x. B x. N) -z B-1 0 B-1 b short form x RHS B-1 A B-1 b B. V. x. B 8

Simplex Procedure x RHS B-1 A B-1 b B. V. x. B è an iteration before minimal: è 1 Find the smallest if all are non-negative, the minimal has been found and stop; else continue. è 2 Identify the entering variable xenter as the xj with the smallest è 3 Identify the leaving variable xleave as xi with the minimal ratio. Stop if the problem is unbounded; else continue. è 4 Identify aleave, enter from xenter and xleave. è 5 Pivot on element aleave, enter to update the whole tableau and go to step 1. 9

Inefficient Simplex Procedure è no guarantee that the smallest number of iterations gives the least opt. è can arbitrarily pick an xj with negative reduced cost as the entering variable è no need to update the whole tableau 10

Minimal Information for the Simplex Procedure x RHS B-1 A B-1 b B. V. x. B minimal information: the set of current basic variables x. B to generate the WHOLE tableau è conceptually, from x. B è è known c. B è known current basis Bcur and hence known (Bcur)-1 è any clever (i. e. , lazy) method to get (Bnew)-1 from (Bcur)-1 without inverting Bnew every time? è the whole tableau from B-1 11

Revised Simplex Algorithm x RHS B-1 A B-1 b B. V. x. B è keeping track of x. B and (Bcur)-1 è entering variable from reduced costs è leaving variable from minimum ratio test è finding (Bnew)-1 from (Bcur)-1 12

Revised Simplex Algorithm è suppose we have the current basic variables x. B, cur and the inverse of the basis (Bcur)-1 è known entities of the tableau: x. B, cur x. N, cur -z B. V. 0 ? 1 x. B I ? 0 RHS (Bcur)-1 b 13

Revised Simplex Algorithm è to find the entering variable xe : calculate for nonbasic variables è stop if all reduced costs are non-negative; else pick the first xj with negative reduced cost as the entering variable x. B, cur x. N, cur z B. V. 0 ? -1 x. B I ? 0 RHS (Bcur)-1 b 14

Revised Simplex Algorithm è to find the leaving variable xl è known column (Bcur)-1 A e of the entering variable xe è with known RHS, execution of minimal ratio test to determine the leaving variable xl (if available) è pivoting on al, e to turn column e into (0, . . , 0, 1, 0. . , 0)T, where “ 1” occurs at the lth row x. B, cur B. V. 0 x. B I xe (Bcur)-1 A e x. N, cur -z ? 1 ? 0 RHS (Bcur)-1 b 15

Equivalence Between Row Operations & Matrix Multiplication è what v should E be to make “v basic in (3)”? w x y v b w x y b making v basic in (3) row operations: (a) (3 ) = (3)/2 (b) (2 ) = (2)+(3 ) (c) (1 ) = (1)-2(3) elementary matrix E = 16

Revised Simplex Algorithm è to find the elementary matrix E that turns A e into è row operations are equivalent to premultiplying by matrix E, where E = I except the lth column, 17

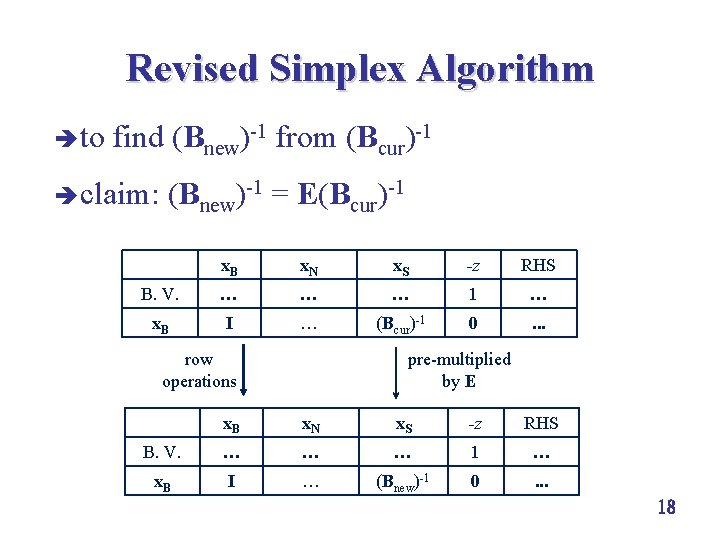
Revised Simplex Algorithm è to find (Bnew)-1 from (Bcur)-1 è claim: (Bnew)-1 = E(Bcur)-1 x. B x. N x. S -z RHS B. V. … … … 1 … x. B I … (Bcur)-1 0 . . . row operations pre-multiplied by E x. B x. N x. S -z RHS B. V. … … … 1 … x. B I … (Bnew)-1 0 . . . 18

Example of Revised Simplex Algorithm è max 2 x 1+x 2 min 2 x 1 x 2, è s. t. –x 1+x 2 2, è x 2 4, è x 1+x 2 8, è x 1, x 2 0. 6, 19

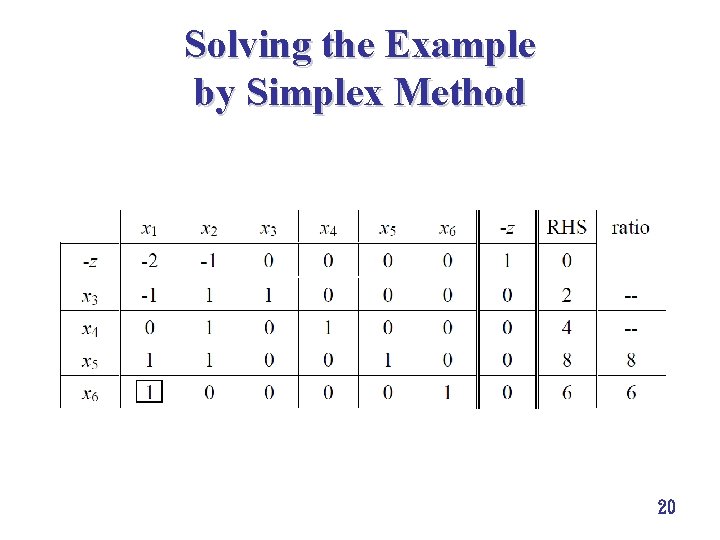
Solving the Example by Simplex Method 20

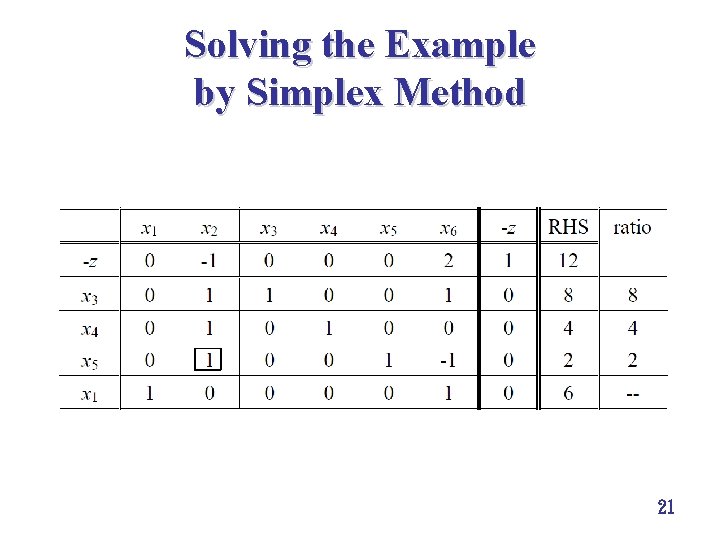
Solving the Example by Simplex Method 21

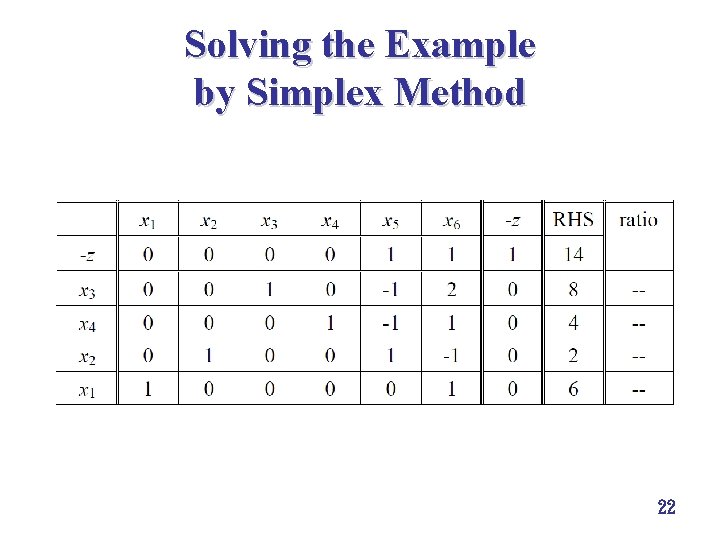
Solving the Example by Simplex Method 22

Example of Revised Simplex Algorithm 23

Relationship Between Revised Simplex and Column Generation è revised è no simplex method need to generate the whole tableau è only generating columns when searching for first negative reduced cost è column generation method è generating necessary column of non-basic variables only when è usually with additional complexity to determine the best entering variable for a given situation 24