Outline relationship among topics secrets LP with upper

Outline è è è relationship among topics secrets LP with upper bounds è by Simplex method è basic è feasible solution (BFS) by Simplex method for bounded variables è extended è optimality conditions for bounded variables è è basic feasible solution (EBFS) ideas of the proof examples Example 1 for ideas but inexact è Example 2 for the exact procedure è 1

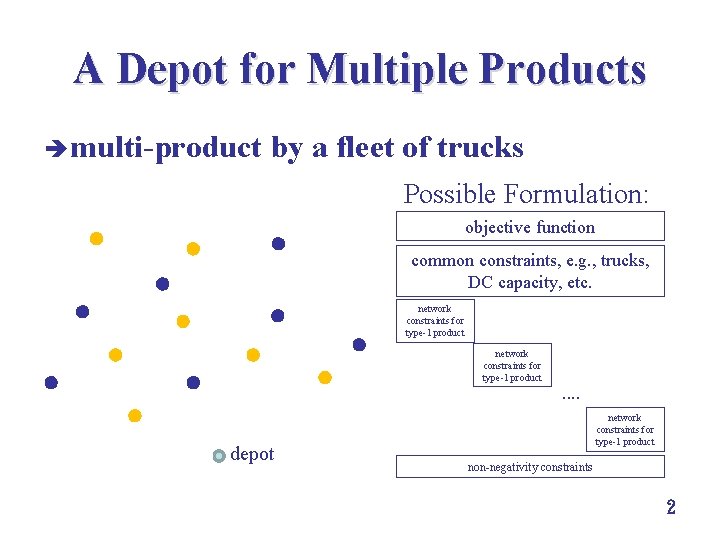
A Depot for Multiple Products è multi-product by a fleet of trucks Possible Formulation: objective function common constraints, e. g. , trucks, DC capacity, etc. network constraints for type 1 product . . depot network constraints for type 1 product non negativity constraints 2

A General Type of Optimization Problems è structure of many problems: è network constraints: easy è other constraints: hard objective function network constraints hard constraints non negativity constraints making use of the easy constraints to solve the problems è solution methods: large-scale optimization è è column generation, Lagrangian relaxation, Dantzig-Wolfe decomposition … è basis: linear programming, network optimization (and also non-linear optimization, integer optimization, combinatorial optimization) 3

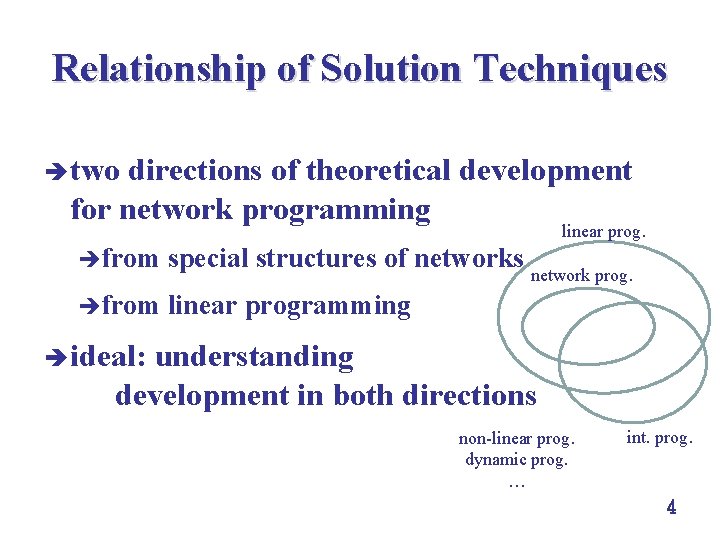
Relationship of Solution Techniques è two directions of theoretical development for network programming linear prog. èfrom special structures of networks network prog. èfrom linear programming è ideal: understanding development in both directions non linear prog. dynamic prog. … int. prog. 4

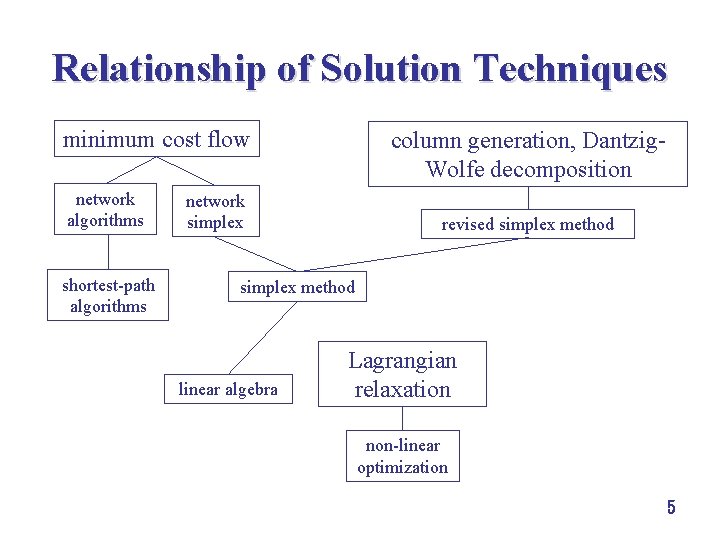
Relationship of Solution Techniques minimum cost flow network algorithms shortest path algorithms column generation, Dantzig Wolfe decomposition network simplex revised simplex method linear algebra Lagrangian relaxation non linear optimization 5

Our Topics è simplex method for bounded variables linkage between LP and network simplex è optimality conditions for minimum cost flow networks è è minimum cost algorithms standard, and successive shortest path è equivalence among network and LP optimality conditions è è è revised simplex column generation Dantzig-Wolfe decomposition Lagrangian relaxation It takes more than one semester to cover these topics in detail! We will only cover the ideas. 6

Secrets 7

The Most Beautiful … 8

Maybe the Most Beautiful of All… è linear algebra geometric properties algebraic properties matrix properties 9

LP with Upper Bounds 10

LP with Upper Bounds è upper bounds: common in network problems, e. g. , an arc with finite capacity è quite some theory of network optimization being from LP 11

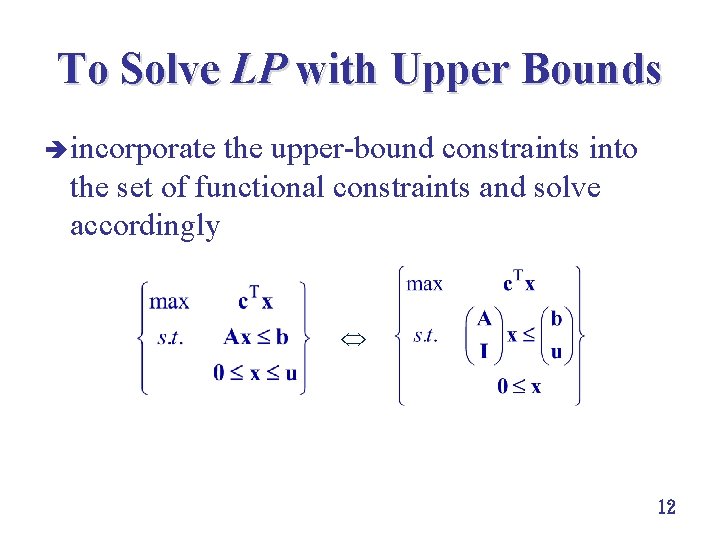
To Solve LP with Upper Bounds è incorporate the upper bound constraints into the set of functional constraints and solve accordingly 12

To Solve LP with Upper Bounds è In the simplex method the lower bound constraints 0 x do not appear in A. è Is it possible to work only with A even with upper bound constraints? è Yes. 13

BFS for Standard LP è Am n, m n, of rank m è basic feasible solution (BFS) x of LP, i. e. , èfeasible: Ax b, 0 x èbasic ènon basic variables: (at least) n m variables = 0 èbasic variables: m non negative variables with linearly independent columns 14

Extended Basic Feasible Solution of LP with Bounded Variables è Am n, m n, of rank m è extended basic feasible solution ( EBFS ) x of LP with bounded variables, i. e. , èfeasible: èbasic Ax b, 0 x u solution ènon basic variables: (at least) n m variables = 0, or = their upper bounds variables: m variables of the form 0 xi ui, with linearly independent columns èBasic 15

Optimality Conditions of Standard LP è Maximum è Conditions: BFS x is maximal if 0 for all non basic variable xj = 0 è Minimum Conditions: BFS è x is minimal if 0 for all non basic variable xj = 0 è intuition : increase of the objective function by unit increase in xj è maximum condition: no good to increase non basic xj è minimum condition: no good to decrease non basic xj è 16

Optimality Conditions of LP with Bounded Variables è Maximum Conditions: EBFS x is maximal if è 0 for all non basic variable xj = 0, and è 0 for all non basic variable xj = uj è Minimum Conditions: EBFS x is minimal if è 0 for all non basic variable xj = 0, and è 0 for all non basic variable xj = uj 17

How to Prove? 18

General Idea è optimality conditions of the EBFS èfrom duality theory and complementary slackness conditions 19

Complementary Slackness Conditions è primal dual pair è Theorem 1 (Complementary Slackness Conditions) èif x primal feasible and y dual feasible èthen x primal optimal and y dual optimal iff xj(y. TA j cj) = 0 for all j, and yi(bi Ai x) = 0 for all i 20

Complementary Slackness Conditions è primal dual pair è Theorem 2 (Necessary and Sufficient Condition) èif x primal feasible èthen x primal optimal iff there exists dual feasible y such that x and y satisfy the Complementary Slackness Conditions 21

Complementary Slackness Conditions for LP with Bounded Variables è by Theorem 2, primal feasible x and dual feasible (y. T, T) are optimal iff èxj(y. TA j + j cj ) = 0, j èyi(bi Ai x) = 0, i è j(uj xj ) = 0, j 22

General Idea of the Proof è optimality conditions of the EBFS è from duality theory and complementary slackness conditions è ideas of the proof è given an EBFS x satisfying the upper bound optimality conditions è then possible to find dual feasible variables (y. T, T)T such that x and (y. T, T)T satisfy the complementary slackness conditions 23

Example 1. Upper-Bound Constraints as Functional Constraints è max 2 x + 5 y, min 2 x 5 y, x + 2 y 20, è s. t. è è è 2 x + y 16, 0 x 2, 0 y 8. 24

Examples of LP with Bounded Variables 25

Example 1. Upper-Bound Constraints as Functional Constraints è min 2 x 5 y, è s. t. è x + 2 y 20, è 2 x + y 16, è 0 x 2, 0 y 8. è max. value = 44 è x* = 2 and y* = 8 26

The following procedure is not exactly the Simplex Method for Bounded Variables. It primarily brings out the ideas of the exact method. 27

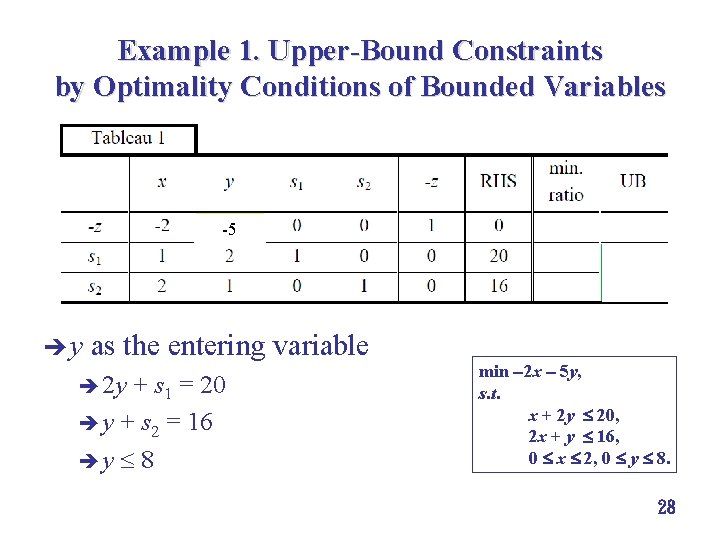
Example 1. Upper-Bound Constraints by Optimality Conditions of Bounded Variables 5 èy as the entering variable è 2 y + s 1 = 20 è y + s 2 = 16 èy 8 min 2 x 5 y, s. t. x + 2 y 20, 2 x + y 16, 0 x 2, 0 y 8. 28

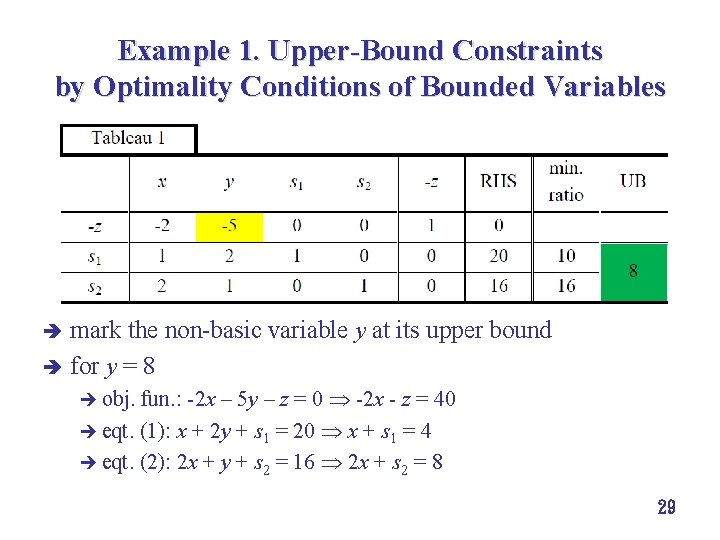
Example 1. Upper-Bound Constraints by Optimality Conditions of Bounded Variables mark the non basic variable y at its upper bound è for y = 8 è fun. : 2 x – 5 y – z = 0 2 x z = 40 è eqt. (1): x + 2 y + s 1 = 20 x + s 1 = 4 è eqt. (2): 2 x + y + s 2 = 16 2 x + s 2 = 8 è obj. 29

Example 1. Upper-Bound Constraints by Optimality Conditions of Bounded Variables èx as the entering variable èx + s 1 = 4 è 2 x èx + s 2 = 8 2 min 2 x 5 y, s. t. x + 2 y 20, 2 x + y 16, 0 x 2, 0 y 8. 30

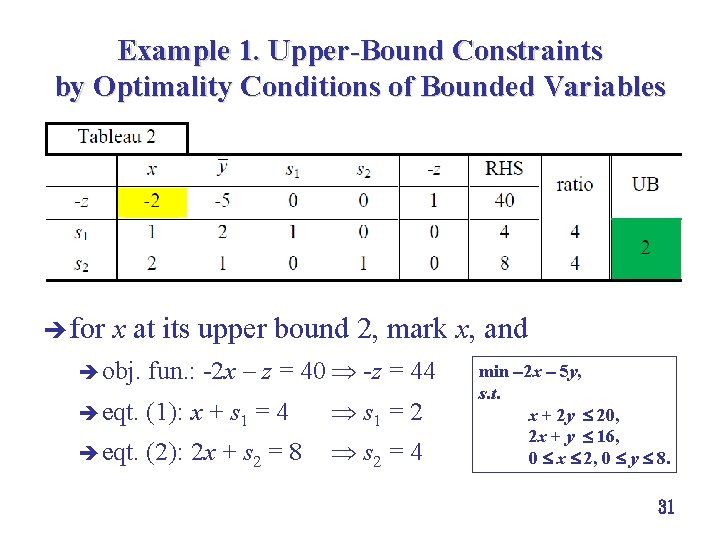
Example 1. Upper-Bound Constraints by Optimality Conditions of Bounded Variables è for x at its upper bound 2, mark x, and è obj. fun. : 2 x – z = 40 z = 44 è eqt. (1): x + s 1 = 4 s 1 = 2 è eqt. (2): 2 x + s 2 = 8 s 2 = 4 min 2 x 5 y, s. t. x + 2 y 20, 2 x + y 16, 0 x 2, 0 y 8. 31

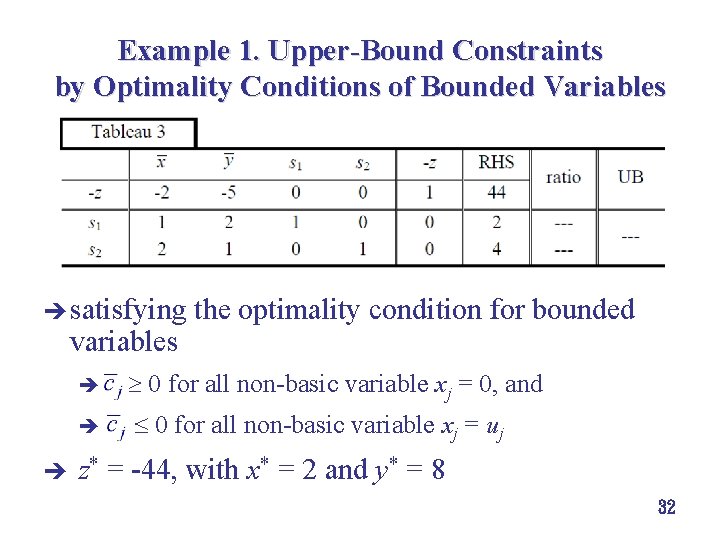
Example 1. Upper-Bound Constraints by Optimality Conditions of Bounded Variables è satisfying variables è è è z* the optimality condition for bounded 0 for all non basic variable xj = 0, and 0 for all non basic variable xj = uj = 44, with x* = 2 and y* = 8 32

Example 1 Being Too Specific è in general, variables swapping among all sorts of status è non-basic at 0 è basic between 0 and upper bound è basic at upper bound è non-basic at upper bound è Simplex method for bounded variables: a special algorithm to record all possibilities 33

The following example follows the exact procedure of the Simplex Method for Bounded Variables. 34

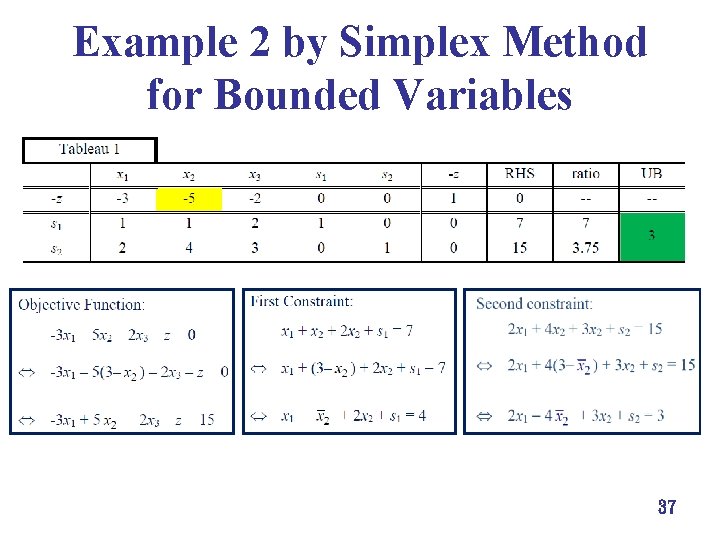
Example 2 è max 3 x 1 + 5 x 2 + 2 x 3 min 3 x 1 5 x 2 2 x 3, è s. t. è x 1 + x 2 + 2 x 3 7, è 2 x 1 + 4 x 2 + 3 x 3 15, è 0 x 1 4, 0 x 2 3, 0 x 3 3. 35

Example 2 by Simplex Method for Bounded Variables è potential entering variable: x 2 è bounded by upper bound 3 è define = u 2 x 2 = 3 x 2 min 3 x 1 5 x 2 2 x 3, s. t. x 1 + x 2 + 2 x 3 7, 2 x 1 + 4 x 2 + 3 x 3 15, 0 x 1 4, 0 x 2 3, 0 x 3 3. 36

Example 2 by Simplex Method for Bounded Variables 37

Example 2 by Simplex Method for Bounded Variables è x 1 as the (potential) entering variable è s 2 as the leaving variable èa min 3 x 1 5 x 2 2 x 3, s. t. x 1 + x 2 + 2 x 3 7, 2 x 1 + 4 x 2 + 3 x 3 15, 0 x 1 4, 0 x 2 3, 0 x 3 3. pivot operation as in standard Simplex Method 38

Example 2 by Simplex Method for Bounded Variables è which can be an entering variable? è can s 1 be a leaving variable? Yes è can x 1 be a leaving variable? Yes min 3 x 1 5 x 2 2 x 3, s. t. x 1 + x 2 + 2 x 3 7, 2 x 1 + 4 x 2 + 3 x 3 15, 0 x 1 4, 0 x 2 3, 0 x 3 3. 39

Example 2 by Simplex Method for Bounded Variables è when = 1. 25, x 1 reaches its upper bound 4 è replace x 1 by and is a basic variable = 0 min 3 x 5 x 2 x , è result s. t. 1 2 3 x 1 + x 2 + 2 x 3 7, 2 x 1 + 4 x 2 + 3 x 3 15, 0 x 1 4, 0 x 2 3, 0 x 3 3. 40

Example 2 by Simplex Method for Bounded Variables è. èa min 3 x 1 5 x 2 2 x 3, s. t. x 1 + x 2 + 2 x 3 7, 2 x 1 + 4 x 2 + 3 x 3 15, 0 x 1 4, 0 x 2 3, 0 x 3 3. “normal” pivot operation with aij < 0 41

Example 2 by Simplex Method for Bounded Variables è minimum è z* min 3 x 1 5 x 2 2 x 3, s. t. x 1 + x 2 + 2 x 3 7, 2 x 1 + 4 x 2 + 3 x 3 15, 0 x 1 4, 0 x 2 3, 0 x 3 3. = 20. 75, x 1* = 4, x 2* = 1. 75, x 3* = 0 42