Outline MOTIVATION CLASSICAL MOLECULAR DYNAMICS TOOLS STRUCTURE OF

Outline MOTIVATION CLASSICAL MOLECULAR DYNAMICS TOOLS STRUCTURE OF NEUTRON STAR MATTER CONCLUSIONS

MOTIVATION Study the structure of neutron star crusts

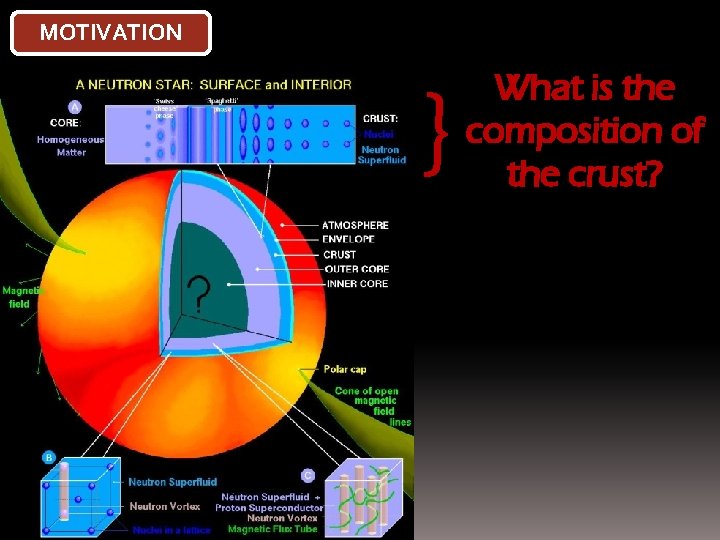
MOTIVATION } What is the composition of the crust?

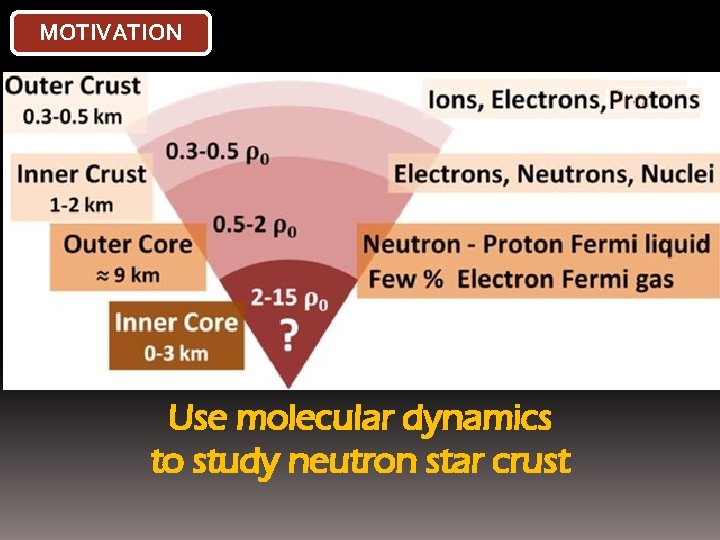
MOTIVATION Use molecular dynamics to study neutron star crust

MOTIVATION Known: Neutron star matter composed of Protons, neutrons and electrons Expected: Structure of neutron star crust is “Pasta” Relevant questions: • Does the structure of the pasta evolves as r, T and isospin asymmetry vary? • Are there phase transitions in NSM? • Does the symmetry energy depend on these structures and phase changes?

MOTIVATION CLASSICAL MOLECULAR DYNAMICS TOOLS STRUCTURE OF NEUTRON STAR MATTER CONCLUSIONS

CLASSICAL MOLECULAR DYNAMICS Classical molecular dynamics - Inter-particle potential - Uses protons & neutrons - Proper dynamics and geometry - Does not use “test particles” - Does not use gaussian density distributions - Produces fragments without external aid - Deexcites fragments naturally - Uses a unique set of parameters But. . . is classic and not quantum

CLASSICAL MOLECULAR DYNAMICS Classical Molecular Dynamics • Potential • Solve equation of motion (Verlet) • Recognize clusters (MSE) • Track evolutions in space-time

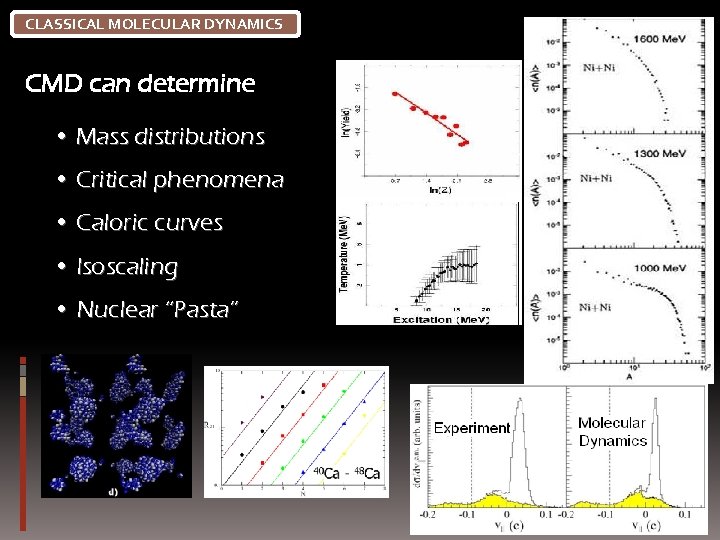
CLASSICAL MOLECULAR DYNAMICS CMD can determine • Mass distributions • Critical phenomena • Caloric curves • Isoscaling • Nuclear “Pasta”

CLASSICAL MOLECULAR DYNAMICS

CLASSICAL MOLECULAR DYNAMICS INFINITE MATTER Procedure to study infinite nuclear matter • Create an infinite system • Select density r • Select temperature • Select isospin content • Equilibrate • Measure • Binding energy E(r, T) • Pressure p(r, T) • Compressibility K(r, T) • Obtain equation of state • Obtain phase diagram • Obtain structure at various r, T, isospin content

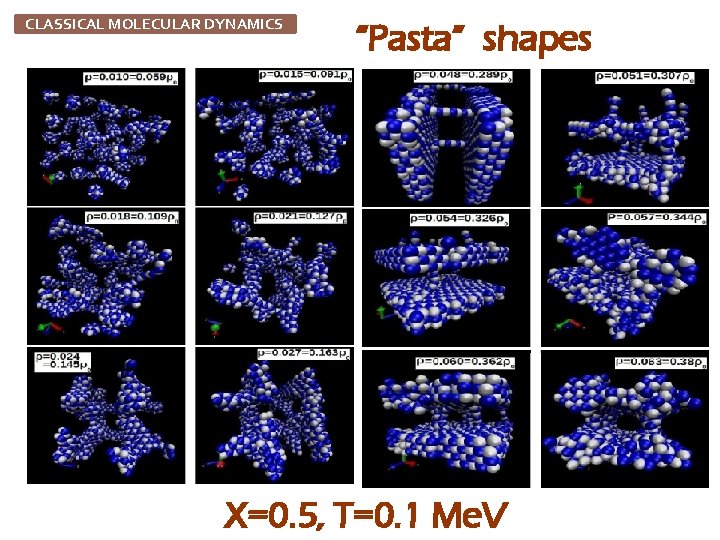
La sa gn a Sp ag he tti Gn oc ch i CLASSICAL MOLECULAR DYNAMICS Pasta !

CLASSICAL MOLECULAR DYNAMICS “Pasta” shapes X=0. 5, T=0. 1 Me. V

Outline MOTIVATION CLASSICAL MOLECULAR DYNAMICS TOOLS STRUCTURE OF NEUTRON STAR MATTER CONCLUSIONS

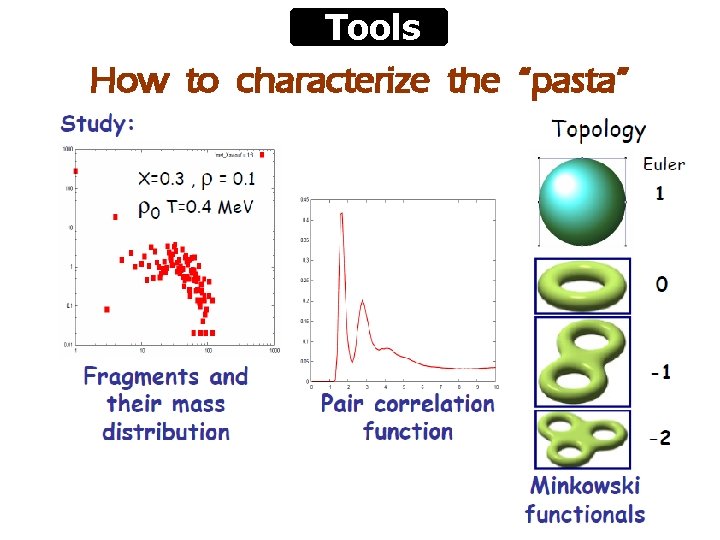
Tools How to characterize the “pasta”

Tools Lindemann coefficient Kolmogorov statistic

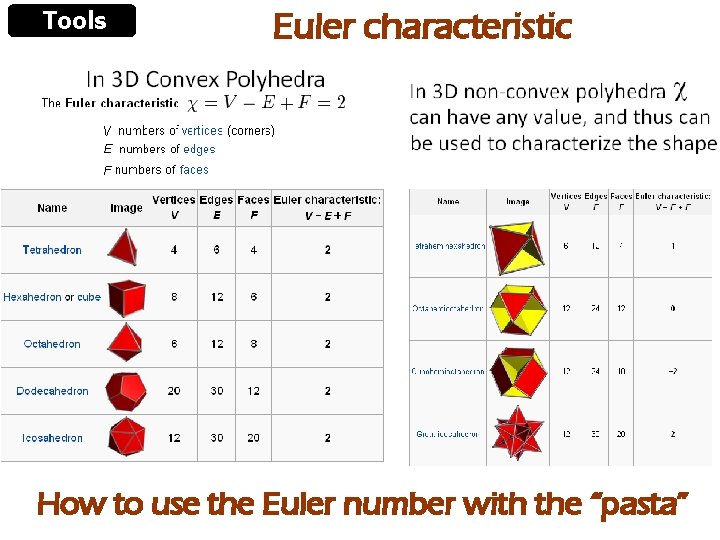
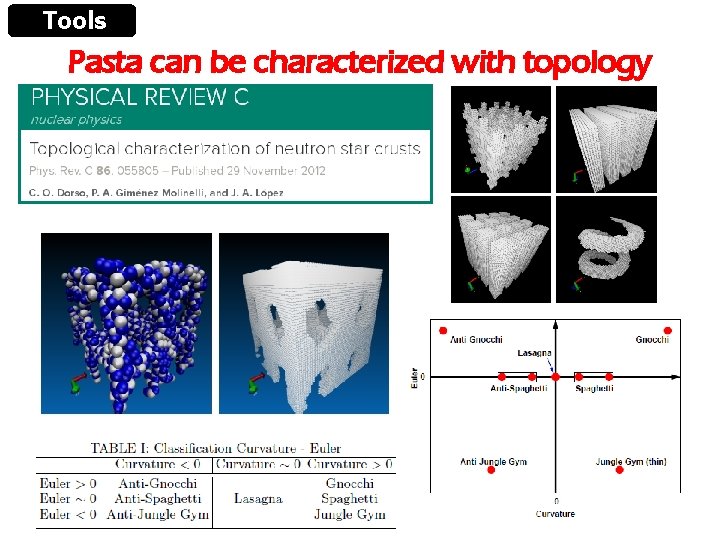
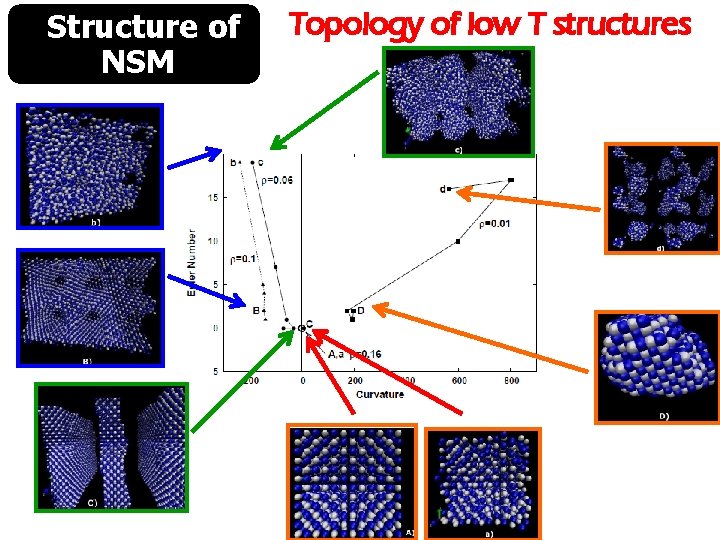
Tools Euler characteristic How to use the Euler number with the “pasta”

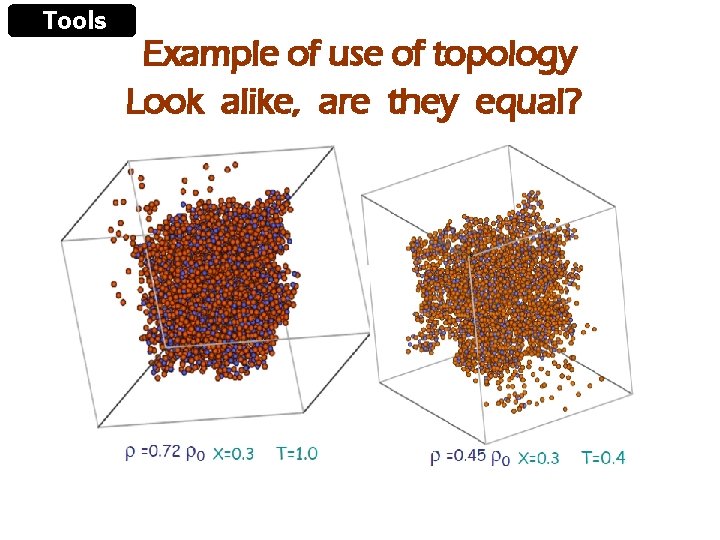
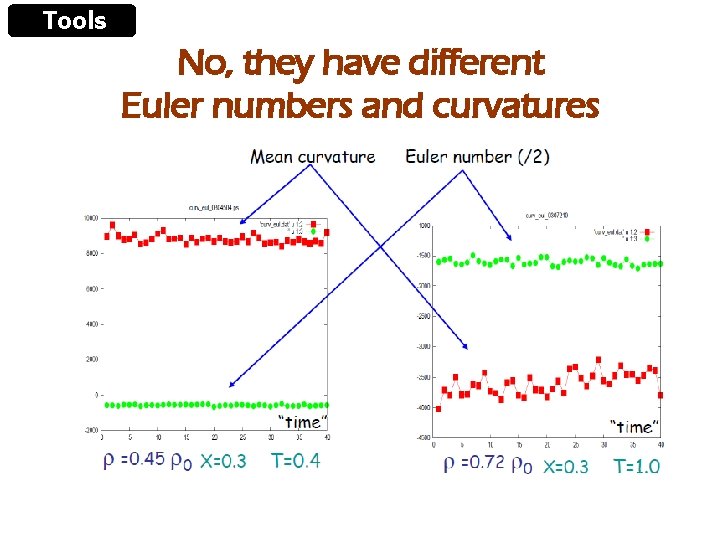
Tools Example of use of topology Look alike, are they equal?

Tools No, they have different Euler numbers and curvatures

Tools Pasta can be characterized with topology

Tools

MOTIVATION CLASSICAL MOLECULAR DYNAMICS TOOLS STRUCTURE OF NEUTRON STAR MATTER CONCLUSIONS

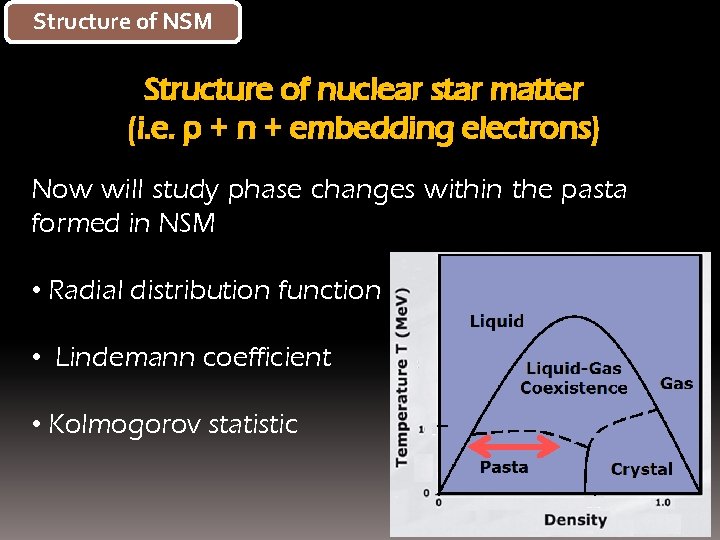
Structure of NSM The structure of the nuclear star matter will be studied using the following tools: • Radial distribution function • Minkowski functionals • Volume, Surface, Curvature • Euler characteristic • Lindemann coefficient • Kolmogorov statistic

Structure of NSM Pasta structures 4000 nucleons, x = 0. 5, T = 0. 2 Me. V Pasta structures for neutron star matter (with screened Coulomb potential) systems with ρ = 0. 05, 0. 06, 0. 07 and 0. 085 fm− 3. Protons are represented in orange, and neutrons in blue.

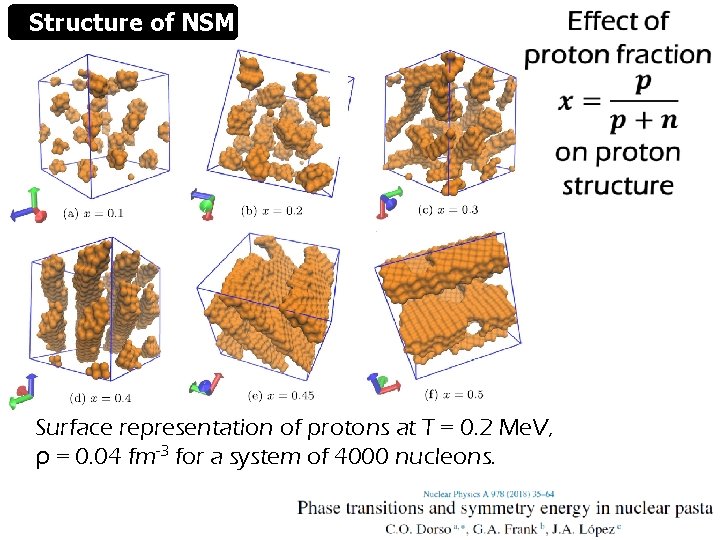
Structure of NSM Surface representation of protons at T = 0. 2 Me. V, ρ = 0. 04 fm-3 for a system of 4000 nucleons.

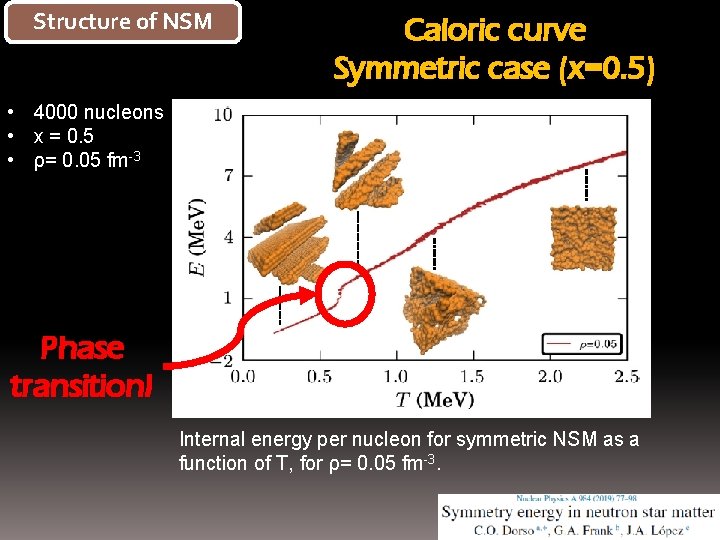
Structure of NSM Caloric curve Symmetric case (x=0. 5) • 4000 nucleons • x = 0. 5 • ρ= 0. 05 fm-3 Phase transition! Internal energy per nucleon for symmetric NSM as a function of T, for ρ= 0. 05 fm-3.

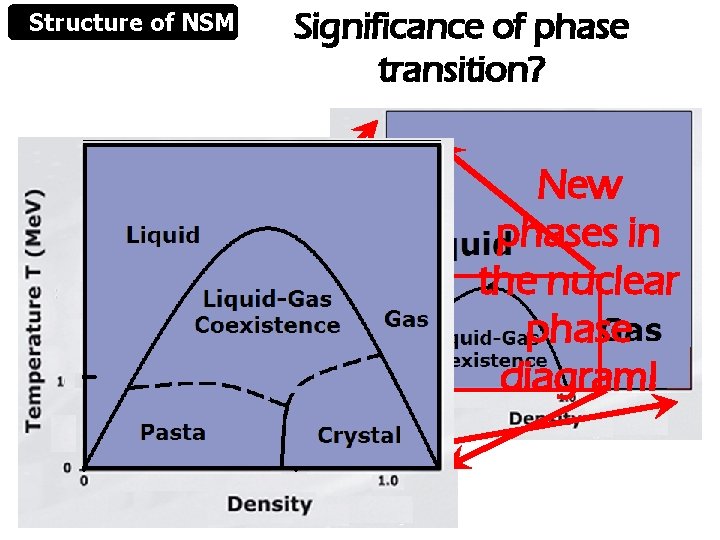
Structure of NSM Significance of phase transition? New phases in the nuclear phase diagram!

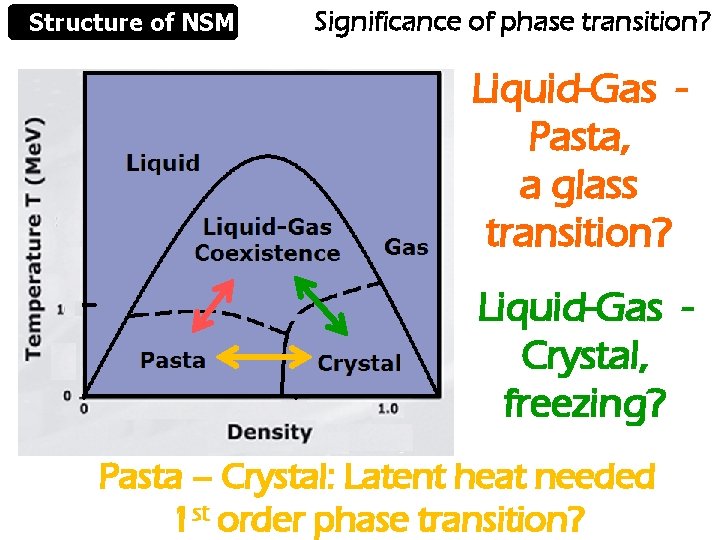
Structure of NSM Significance of phase transition? Liquid-Gas Pasta, a glass transition? Liquid-Gas Crystal, freezing? Pasta – Crystal: Latent heat needed 1 st order phase transition?

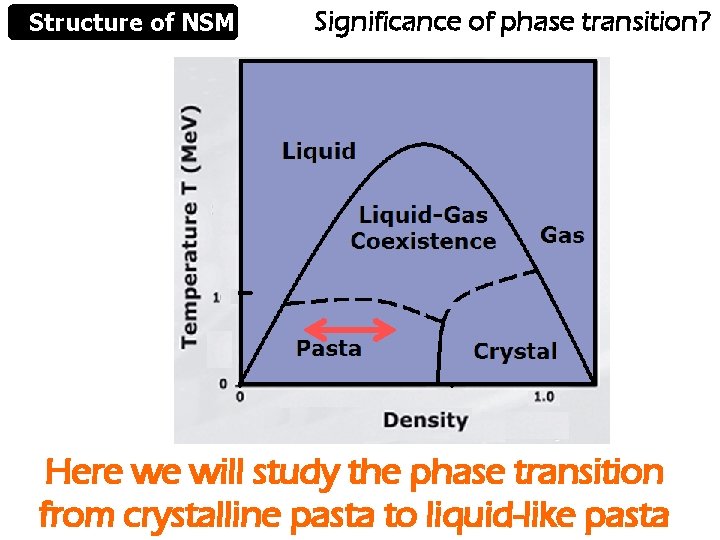
Structure of NSM Significance of phase transition? Here we will study the phase transition from crystalline pasta to liquid-like pasta

Structure of NSM Structure of nuclear star matter (i. e. p + n + embedding electrons) Now will study phase changes within the pasta formed in NSM • Radial distribution function • Lindemann coefficient • Kolmogorov statistic

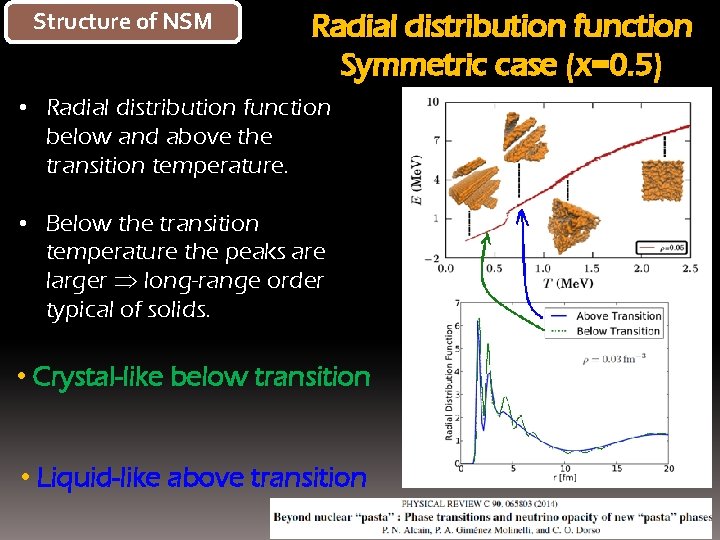
Structure of NSM Radial distribution function Symmetric case (x=0. 5) • Radial distribution function below and above the transition temperature. • Below the transition temperature the peaks are larger long-range order typical of solids. • Crystal-like below transition • Liquid-like above transition

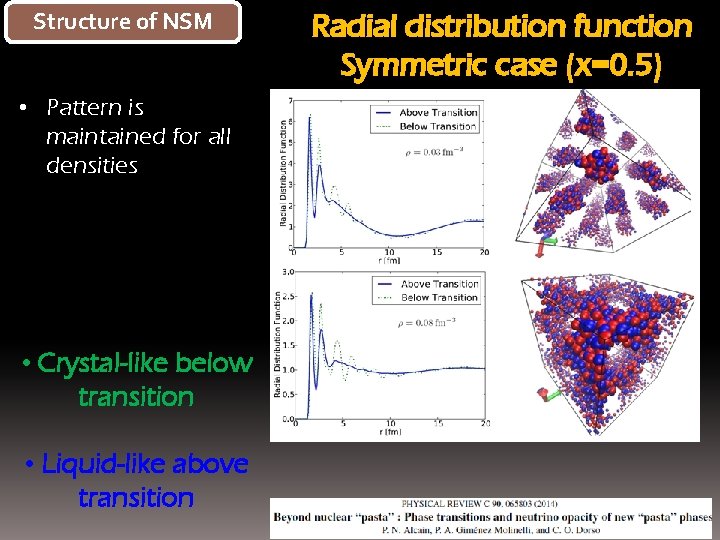
Structure of NSM • Pattern is maintained for all densities • Crystal-like below transition • Liquid-like above transition Radial distribution function Symmetric case (x=0. 5)

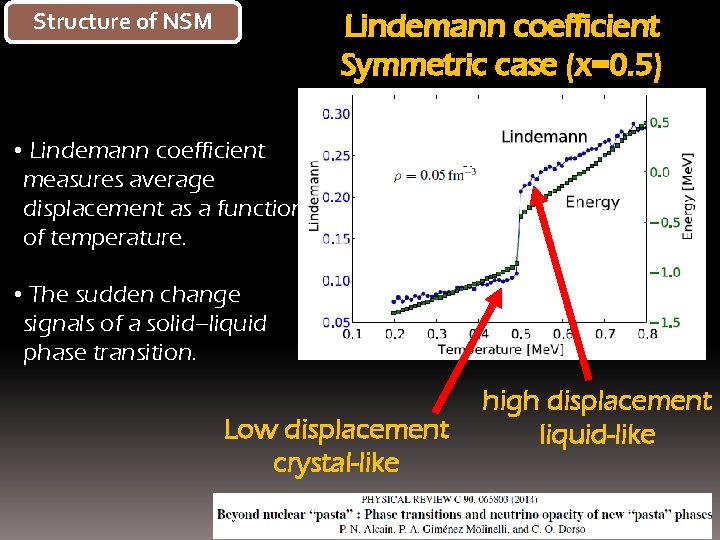
Structure of NSM Lindemann coefficient Symmetric case (x=0. 5) • Lindemann coefficient measures average displacement as a function of temperature. • The sudden change signals of a solid–liquid phase transition. Low displacement crystal-like high displacement liquid-like

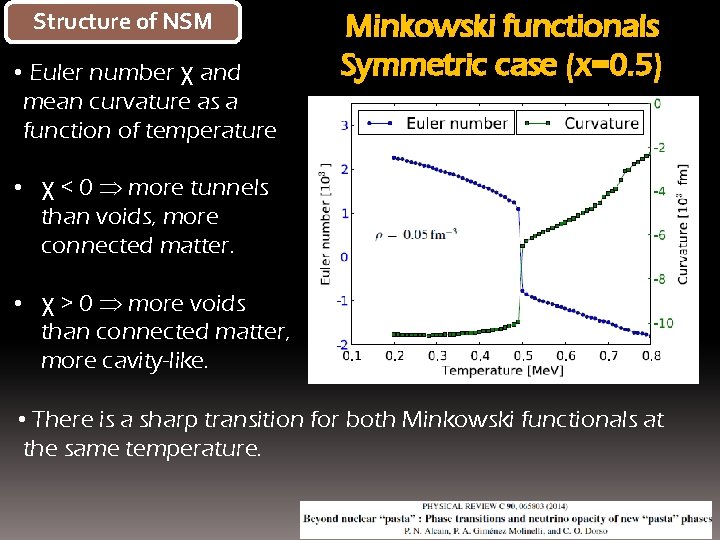
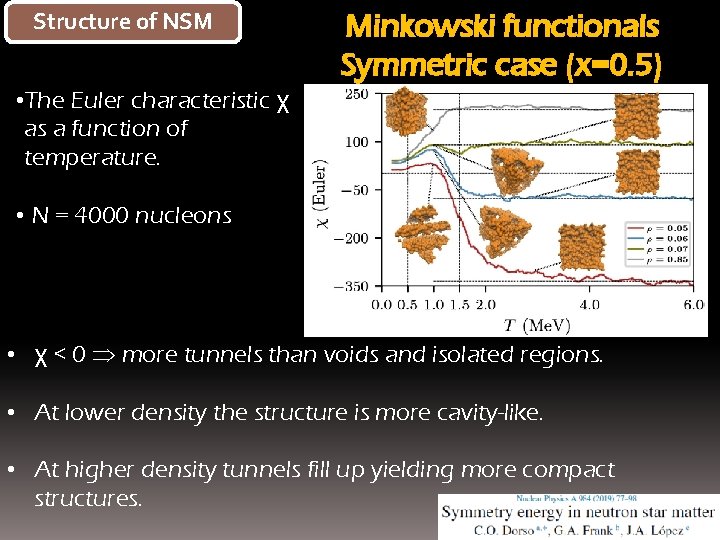
Structure of NSM • Euler number χ and mean curvature as a function of temperature Minkowski functionals Symmetric case (x=0. 5) • χ < 0 more tunnels than voids, more connected matter. • χ > 0 more voids than connected matter, more cavity-like. • There is a sharp transition for both Minkowski functionals at the same temperature.

Structure of NSM Minkowski functionals Symmetric case (x=0. 5) • The Euler characteristic χ as a function of temperature. • N = 4000 nucleons • χ < 0 more tunnels than voids and isolated regions. • At lower density the structure is more cavity-like. • At higher density tunnels fill up yielding more compact structures.

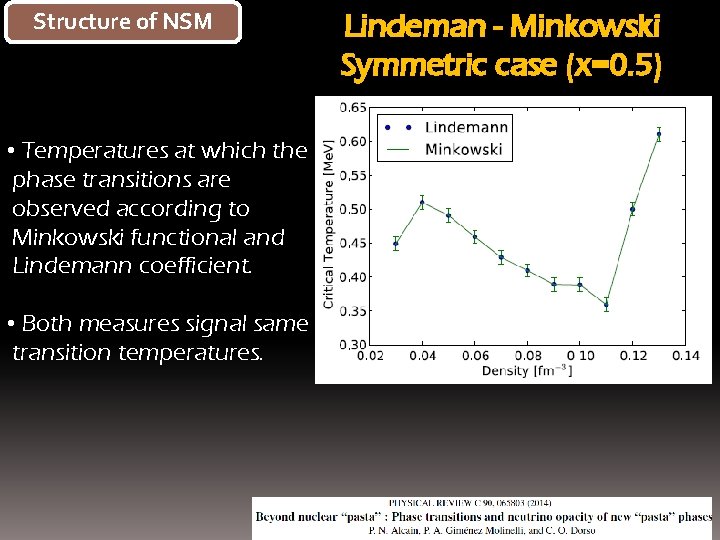
Structure of NSM • Temperatures at which the phase transitions are observed according to Minkowski functional and Lindemann coefficient. • Both measures signal same transition temperatures. Lindeman - Minkowski Symmetric case (x=0. 5)

Structure of NSM Now will study phase changes within the pasta formed in NSM with x = 0. 1, 0. 2, 0. 3, 0. 4, 0. 5 • Radial distribution function • Euler characteristic • Kolmogorov statistic

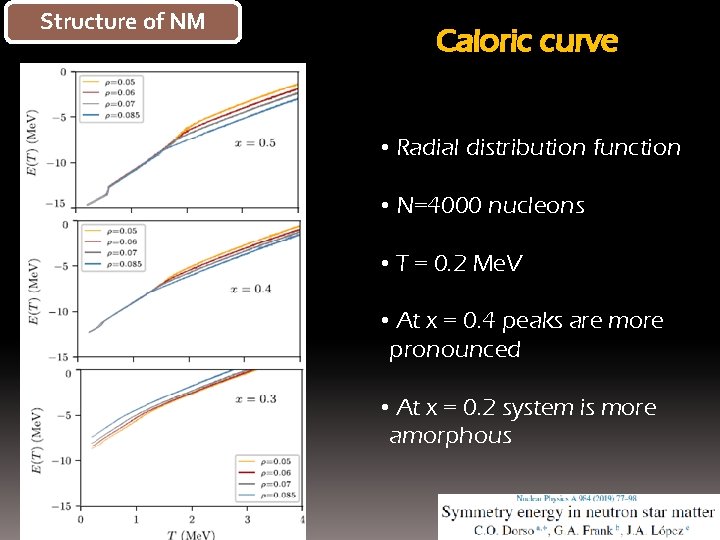
Structure of NSM Radial Distribution function • Radial distribution function • N=4000 nucleons • T = 0. 2 Me. V • At x = 0. 4 peaks are more pronounced • At x = 0. 2 system is more amorphous

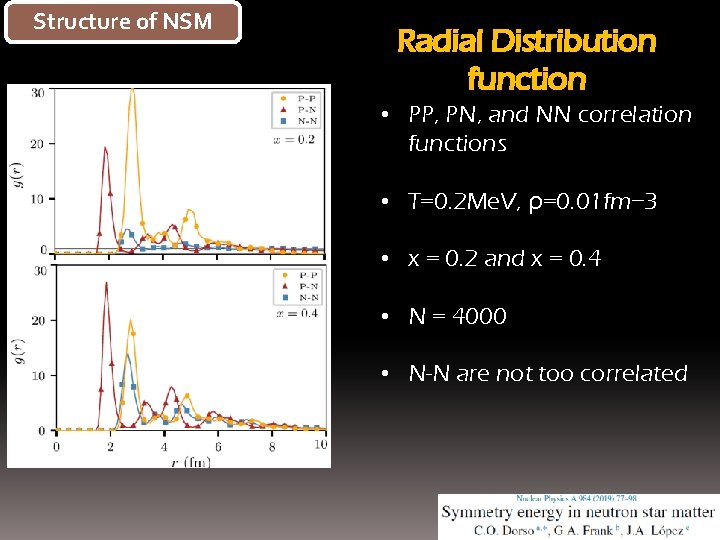
Structure of NSM Radial Distribution function • PP, PN, and NN correlation functions • T=0. 2 Me. V, ρ=0. 01 fm− 3 • x = 0. 2 and x = 0. 4 • N = 4000 • N-N are not too correlated

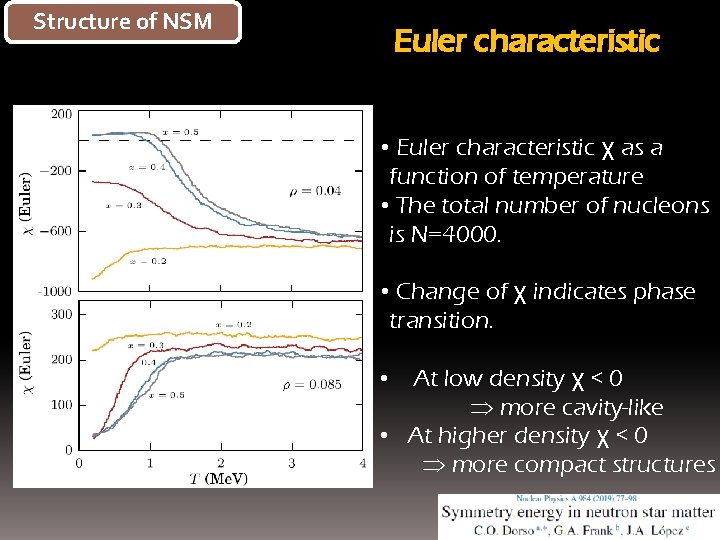
Structure of NSM Euler characteristic • Euler characteristic χ as a function of temperature • The total number of nucleons is N=4000. • Change of χ indicates phase transition. • At low density χ < 0 more cavity-like • At higher density χ < 0 more compact structures

MOTIVATIONS CLASSICAL MOLECULAR DYNAMICS TOOLS STRUCTURE OF NEUTRON STAR MATTER CONCLUSIONS

- Pasta structures are formed at low temperatures and subcritical densities - Topology helps to study shapes of pasta

- Pastas show liquid-solid and solid-crystal phase transitions within the pastas. - A morphological re-arrangement of the pasta structures occurs as the proton fraction diminishes.

- The lowest explored proton fraction x = 0. 1 attains a gnocchi-like structure. - Gnocchis themselves experience (inner) topological changes during its formation process.

Current work: • Isospin-dependent phase diagram of nuclear matter • Momentum-dependent potentials • introduction of Pauli exclusion principle

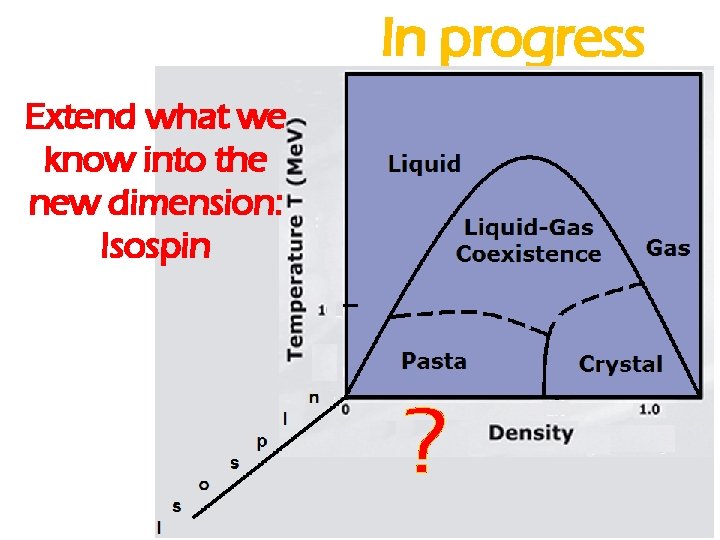
In progress Extend what we know into the new dimension: Isospin ?

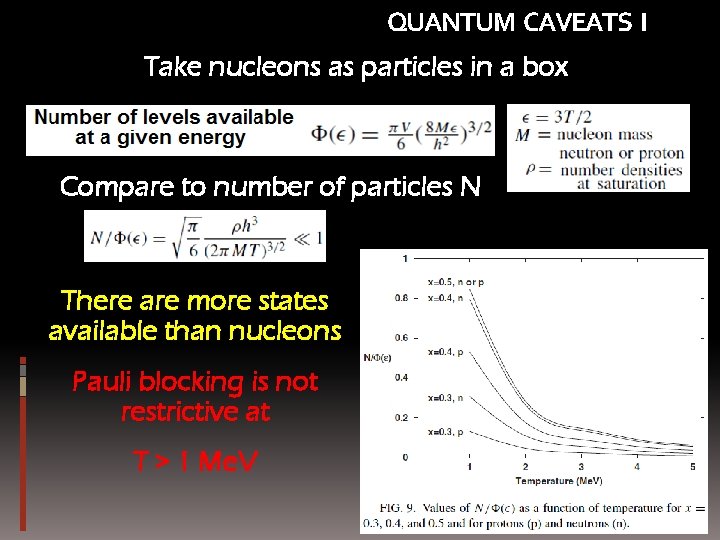
QUANTUM CAVEATS I Take nucleons as particles in a box Compare to number of particles N There are more states available than nucleons Pauli blocking is not restrictive at T > 1 Me. V

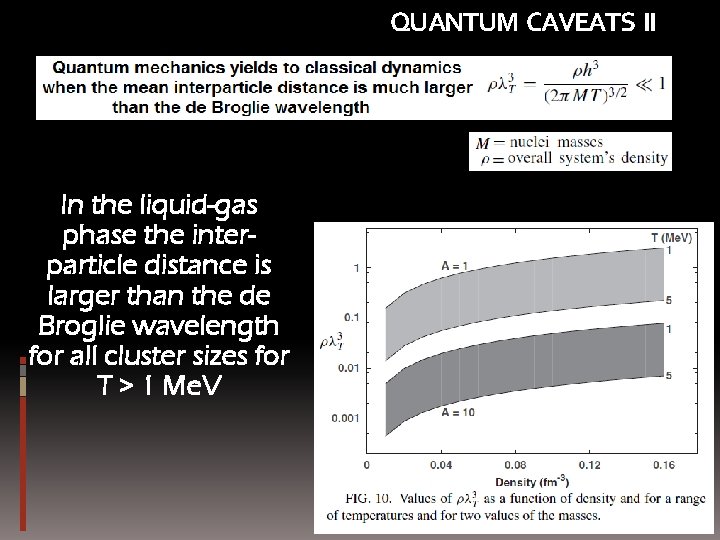
QUANTUM CAVEATS II In the liquid-gas phase the interparticle distance is larger than the de Broglie wavelength for all cluster sizes for T > 1 Me. V

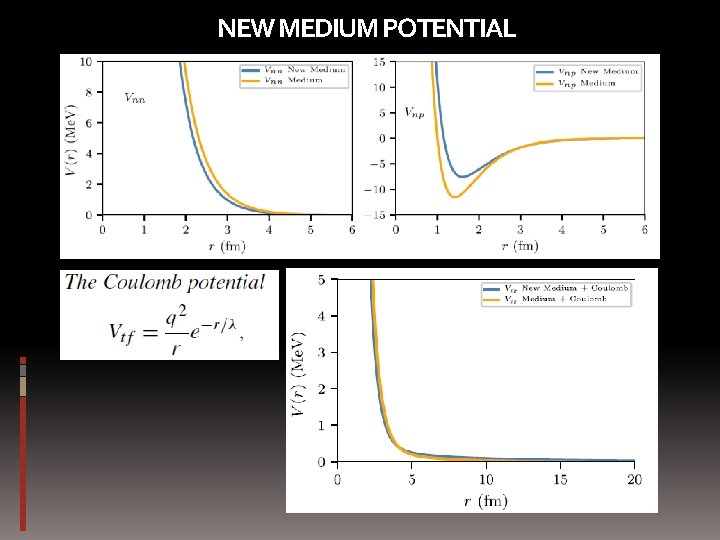
NEW MEDIUM POTENTIAL

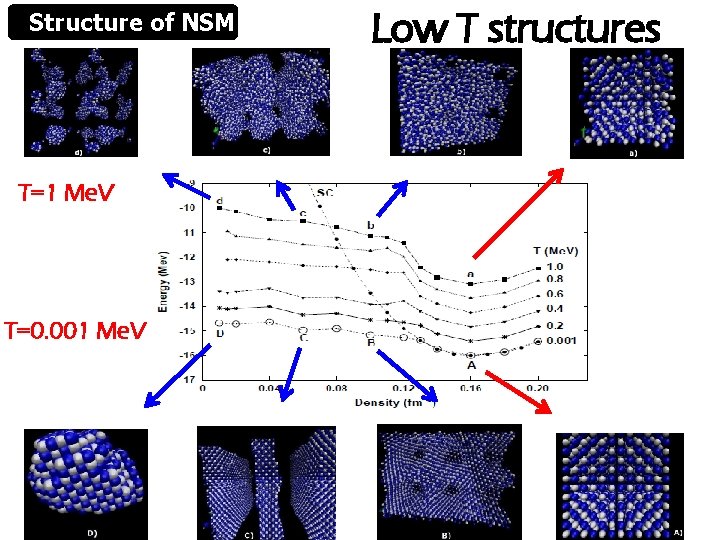
Structure of NSM Topology of low T structures

Structure of NSM T=1 Me. V T=0. 001 Me. V Low T structures

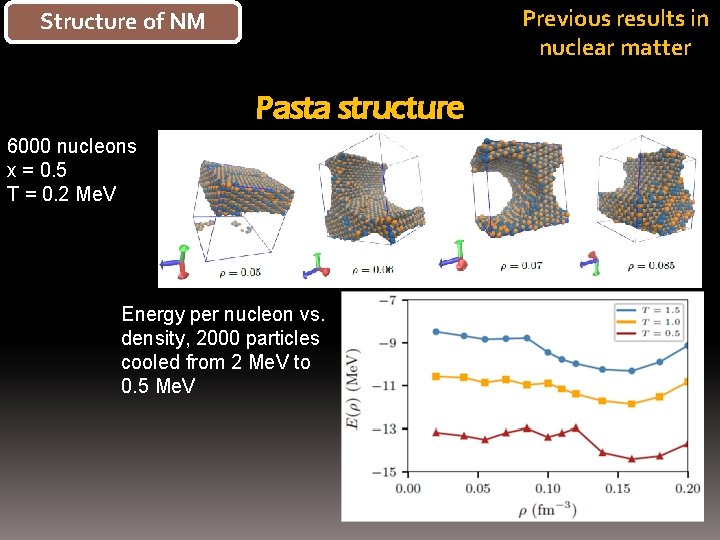
Structure of NM Previous study of nuclear matter (i. e. no embedding electrons)

Previous results in nuclear matter Structure of NM Pasta structure 6000 nucleons x = 0. 5 T = 0. 2 Me. V Energy per nucleon vs. density, 2000 particles cooled from 2 Me. V to 0. 5 Me. V

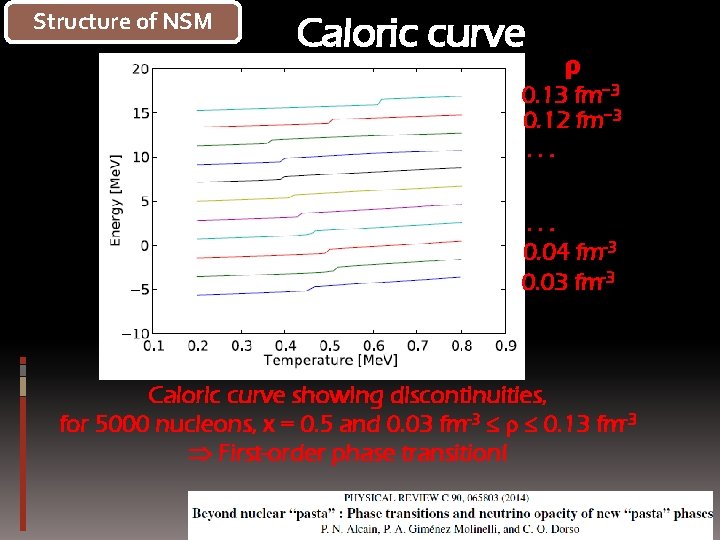
Structure of NSM Caloric curve ρ 0. 13 fm− 3 0. 12 fm− 3. . . 0. 04 fm-3 0. 03 fm-3 Caloric curve showing discontinuities, for 5000 nucleons, x = 0. 5 and 0. 03 fm-3 r 0. 13 fm-3 First-order phase transition!

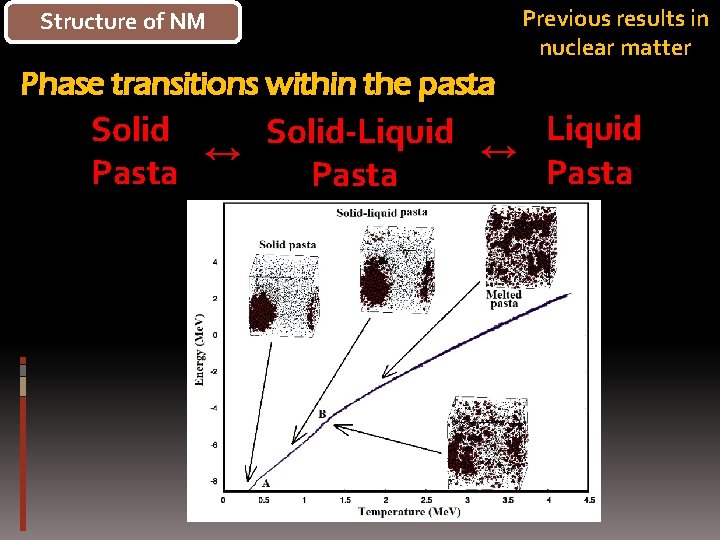
Structure of NM Previous results in nuclear matter Phase transitions within the pasta Liquid Solid-Liquid ↔ ↔ Pasta

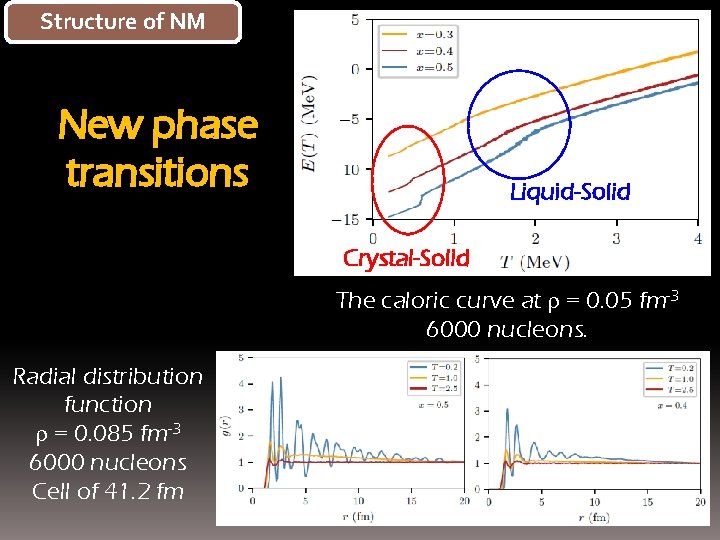
Structure of NM New phase transitions Liquid-Solid Crystal-Solid The caloric curve at r = 0. 05 fm-3 6000 nucleons. Radial distribution function r = 0. 085 fm-3 6000 nucleons Cell of 41. 2 fm

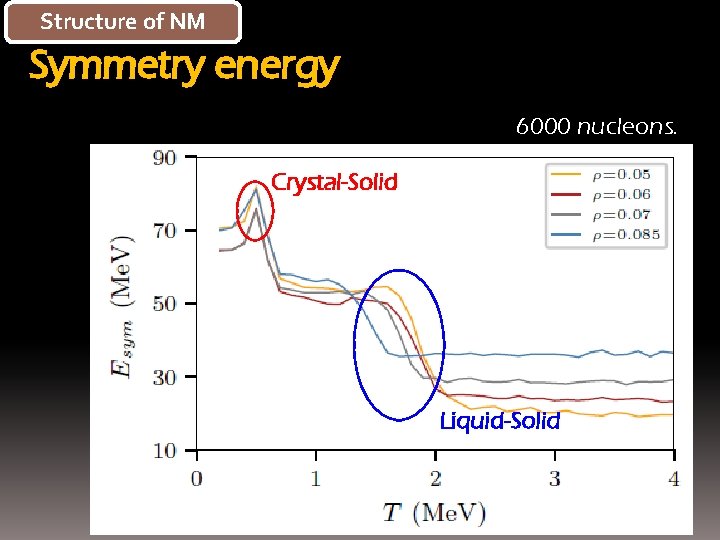
Structure of NM Symmetry energy 6000 nucleons. Crystal-Solid Liquid-Solid

Structureof of. NSM NM Caloric curve • Radial distribution function • N=4000 nucleons • T = 0. 2 Me. V • At x = 0. 4 peaks are more pronounced • At x = 0. 2 system is more amorphous