Outline Linear Shiftinvariant system Linear filters Fourier transformation

Outline • Linear Shift-invariant system • Linear filters • Fourier transformation – Time and frequency representation • Filter Design 10/31/2020 Visual Perception Modeling 1

Linear System Theory • What is a system? – A system is anything that accepts an input and produces an output in response y[n] = T{x[n]} where x[n] is the input sequence and y[n] is the output sequence in responses to x[n] – How to represent a sequence? 10/31/2020 Visual Perception Modeling 2

Linear System • Linearity – y 1[n] = T{x 1[n]} – y 2[n] = T{x 2[n]} – Then – y 1[n]+y 2[n] = T{x 1[n]+x 2[n]} 10/31/2020 Visual Perception Modeling 3

Shift-Invariant System • Shift invariance – y[n] = T{x[n]} – y[n-T] = T{x[n-T]} • LSI system – A LSI system is completely characterized by its impulse response h[n] – For any other input, we can obtain the response through convolution 10/31/2020 Visual Perception Modeling 4

Filtering • Closely related to convolution • Filter examples – Smoothing by averaging – Smoothing by Gaussian 10/31/2020 Visual Perception Modeling 5

Multi-scale Representation • Scale in the Gaussian function – is the standard deviation of the Gaussian distribution – When is small, no smoothing or very little – When is large, the noise will be largely disappear. However, the image detail will disappear along with the noise 10/31/2020 Visual Perception Modeling 6

Gaussian Pyramid 10/31/2020 Visual Perception Modeling 7

Why Gaussian Smoothing? • Scale space – If we convolve a Gaussian with a Gaussian, it will also be a Gaussian – Efficiency • A small kernel is generally enough • Separable – Central limit theorem 10/31/2020 Visual Perception Modeling 8

Spatial Frequency Analysis • Filter response analysis – For example, why does smoothing reduce noise? – What is the difference between the discrete image representation and a continuous surface representation? – Is there any way we can design the best filter for a certain task? • For smoothing, how can we have the best smoothing kernel? 10/31/2020 Visual Perception Modeling 9

Fourier Transforms • Fourier transform – The transformation takes a complex valued function x, y and returns a complex valued function of u, v – U and v determine the spatial frequency and orientation of the sinusoidal component 10/31/2020 Visual Perception Modeling 10

Inverse Fourier Transform • Inverse Fourier transform – It recovers a signal from its Fourier transform 10/31/2020 Visual Perception Modeling 11

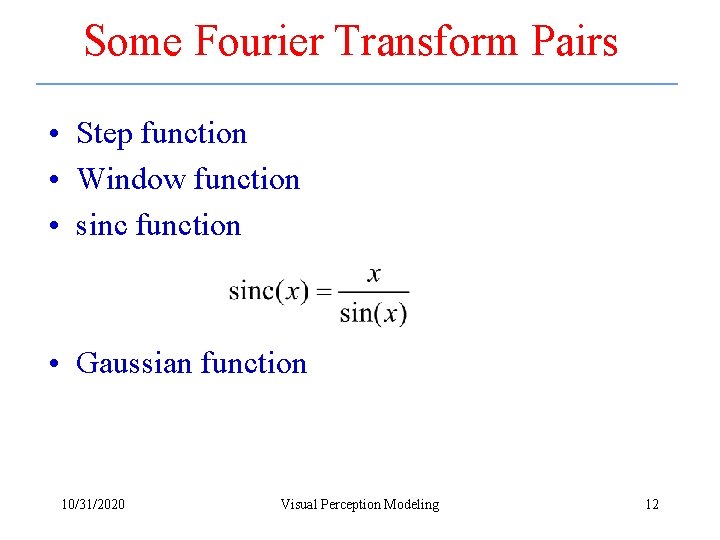
Some Fourier Transform Pairs • Step function • Window function • sinc function • Gaussian function 10/31/2020 Visual Perception Modeling 12

Filter Design • Design filters to accomplish particular goals • Lowpass filters – Reduce the amplitude of high-frequency components – Can reduce the visible effects of noise – Box filter – Triangle filter – High-frequency cutoff – Gaussian lowpass filter 10/31/2020 Visual Perception Modeling 13

Filter Design – cont. • Bandpass and bandstop filters • Highpass filters • Optimal filter design – In some sense, optimal of doing a particular job – Establish a criterion of performance and then maximize the criterion by proper selection of the impulse response – Wiener estimator – Wiener deconvolution 10/31/2020 Visual Perception Modeling 14

Other Transformations • Fourier transform is one of a number of linear transformations that are useful in image processing • Basis functions – How to represent an image by weighted sum of some functions of our choice? 10/31/2020 Visual Perception Modeling 15

Principal Component Analysis • Optimal representation with fewer basis functions – We want to design a set of basis functions such that we can reconstruct the original image with smallest possible error with a given number of basis functions 10/31/2020 Visual Perception Modeling 16

PCA for Face Recognition 10/31/2020 Visual Perception Modeling 17

PCA for Face Recognition – cont. First 20 principal components 10/31/2020 Visual Perception Modeling 18

PCA for Face Recognition – cont. Components with low eigenvalues 10/31/2020 Visual Perception Modeling 19

PCA for Face Recognition – cont. 10/31/2020 Visual Perception Modeling 20