Outline Introduction Signal random variable random process and

Outline Introduction Signal, random variable, random process and spectra Analog modulation Analog to digital conversion Digital transmission through baseband channels Signal space representation Optimal receivers Digital modulation techniques Channel coding Synchronization Information theory Communications Engineering 1

Signal, random variable, random process and spectra Communications Engineering 2

Signal, random variable, random process and spectra Signals Review of probability and random variables Random processes: basic concepts Gaussian and White processes Selected from Chapter 2. 1 -2. 6, 5. 1 -5. 3 Communications Engineering 3

Signal In communication systems, a signal is any function that carries information. Also called information bearing signal Communications Engineering 4

Signal Continuous-time signal vs. discrete-time signal Continuous-valued signal vs. discrete-valued signal Continuous-time continuous-valued: analog signal Discrete-time and discrete-valued: digital signal Discrete-time and continuous-valued : sampled signal Continuous-time and discrete-valued: quantized signal Communications Engineering 5

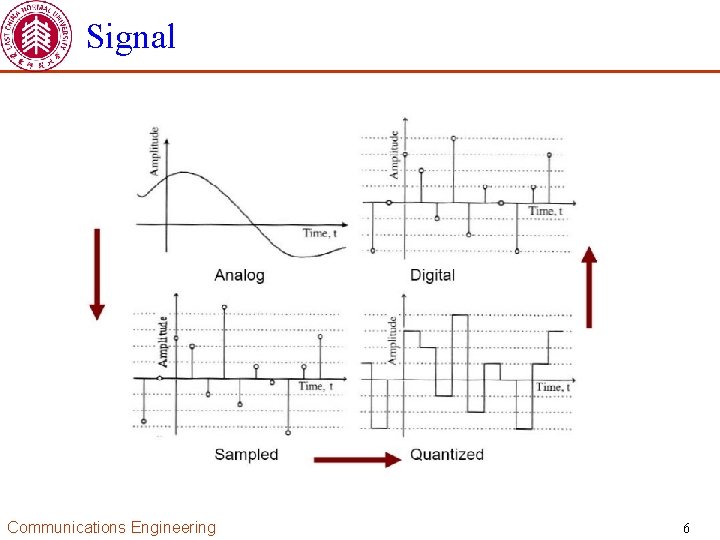
Signal Communications Engineering 6

Signal Energy vs. power signal Ø Energy Ø Power Ø A signal is an energy signal iff energy is limited Ø A signal is a power signal iff power is limited Communications Engineering 7

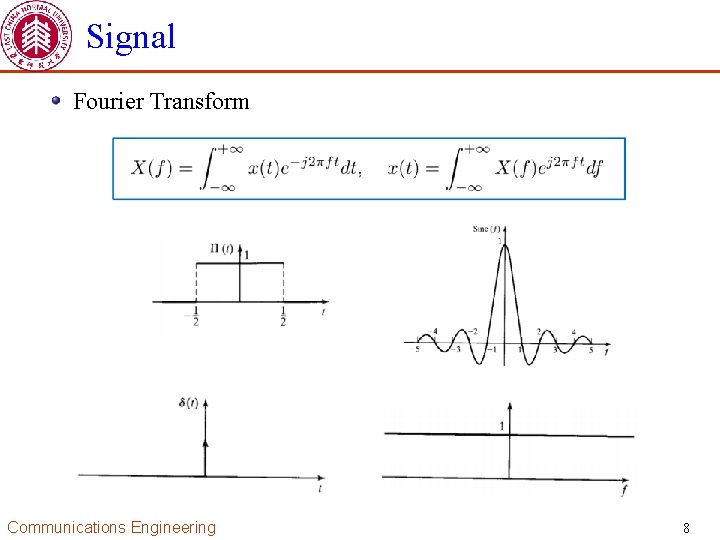
Signal Fourier Transform Communications Engineering 8

Random variable Review of probability and random variables Ø Two events A and B Ø Conditional probability P(A|B) Ø Joint probability P(AB)=P(A)P(B|A)=P(B)P(A|B) Ø A and B are independent iff P(AB)=P(A)P(B) Ø Let be mutually exclusive events with. Then for any event , we have Communications Engineering 9

Random variable Review of probability and random variables Ø Bayes’ Rule: Let be mutually exclusive such that. For any nonzero probability event B, we have Communications Engineering 10

Random variable Review of probability and random variables Consider a binary communication system Communications Engineering 11

Random variable Review of probability and random variables Ø A random variable is a mapping from the sample space to the set of real numbers Ø Discrete r. v. : range is finite ({0, 1}) or countable infinite ({0, 1, …}) Ø Continuous r. v. : range is uncountable infinite (real number) Communications Engineering 12

Random variable Review of probability and random variables Ø The cumulative distribution function (CDF) of a r. v. X is Ø The key properties of CDF Communications Engineering 13

Random variable Review of probability and random variables Ø The probability density function (PDF) of a r. v. X is Ø The key properties of PDF Communications Engineering 14

Random variable Review of probability and random variables Ø Common random variables: Bernoulli, Binomial, Uniform, and Gaussian Ø Bernoulli distribution: Ø Binomial distribution: the sum of n independent Bernoulli r. v. Communications Engineering 15

Random variable Review of probability and random variables Ø Suppose that we transmit a 31 -bit sequence with error correction capability up to 3 bit errors Ø If the probability of a bit error is p=0. 001, what is the probability that the sequence received is in error? Ø On the other hand, if no error correction is used, the error probability is Communications Engineering 16

Random variable Review of probability and random variables Ø Uniform distribution: Ø The random phase of a sinusoid is often modeled as a uniform r. v. between 0 and Ø The mean or expected value of X is first moment of X Communications Engineering 17

Random variable Review of probability and random variables Ø The n-th moment of X Ø If n=2, we have the mean-squared value of X Ø The n-th central moment is Ø If n=2, we have the variance of X Ø is called the standard deviation Communications Engineering 18

Random variable Review of probability and random variables Ø Gaussian distribution: Ø A Gaussian r. v. is completely determined by its mean and variance, and hence usually denoted as The most important distribution in communications! Communications Engineering 19

Random variable Review of probability and random variables Ø Q-function is a standard form to express error probabilities without a closed-form Ø The Q-function is the area under the tail of a Gaussian pdf with mean 0 and variance 1 Extremely important in error probability analysis! Communications Engineering 20

Random variable Review of probability and random variables Ø Some key properties of Q-function 1. Q-function is monotonically decreasing 2. 3. Craig’s alternative form of Q-function 4. Upperbound 5. For a Gaussian variable Communications Engineering 21

Random variable Review of probability and random variables Ø Joint distribution of two r. v. s X and Y is And joint PDF is Communications Engineering 22

Random variable Review of probability and random variables Ø Marginal distribution Ø Marginal density Ø X and Y are said to be independent iff Communications Engineering 23

Random variable Review of probability and random variables Ø Correlation of the two r. v. s X and Y is Ø Correlation of the two centered r. v. s X-E[X] and YE[Y] is called the covariance of X and Y Ø If called uncorrelated. Communications Engineering then X and Y are 24

Random variable Review of probability and random variables Ø The covariance of X and Y normalized w. r. t. referred to the correlation coefficient of X and Y is Ø If X and Y are independent, then they are uncorrelated. Ø The converse is not true except for the Gaussian r. v. Communications Engineering 25

Random variable Review of probability and random variables Ø Functions of random variable. Ø How to obtain the PDF of r. v. ? Ø Two steps: 1. Calculate the CDF of Y through 2. Take the derivative of CDF Ø For r. v. s , generally Communications Engineering 26

Random variable Review of probability and random variables Ø are jointly Gaussian iff Communications Engineering 27

Random variable Review of probability and random variables Ø In case of n=2, we have Communications Engineering 28

Random variable Review of probability and random variables Ø And if X 1 and X 2 are uncorrelated, i. e. , If X 1 and X 2 are Gaussian and uncorrelated, they are independent. Communications Engineering 29

Random variable Review of probability and random variables Ø If n random variables are jointly Gaussian, then any set of them is also jointly Gaussian. Ø Jointly Gaussian r. v. s are completely characterized by mean vector and the covariance matrix. Ø Any linear combination of the n r. v. s is Gaussian. Communications Engineering 30

Random variable Review of probability and random variables Ø Law of large numbers Consider a sequence of r. v. , let if the r. v. s are uncorrelated with the same mean variance , then , , and The average r. v. converges to the mean value Communications Engineering 31

Random variable Review of probability and random variables Ø Central limit theorem If variance are i. i. d. r. v. s with same mean , then , and Thermal noise results from the random movements of many electrons is well modeled by a Gaussian distribution. Communications Engineering 32

Random variable Review of probability and random variables Ø Consider for example a sequence of uniform distribution r. v. s with mean 0 and variance 1/12, then n=2 n=1 n=4 n=8 Dashed line: Solid line: Communications Engineering 33

Random variable Review of probability and random variables Ø Rayleigh distribution: Rayleigh distribution is usually used to model fading for nonline-of-sight (NLOS) signal transmissions. Very important distribution for analysis in mobile and wireless communications. Communications Engineering 34

Random variable Review of probability and random variables Ø Consider for example h=a+jb, where a and b are i. i. d. Gaussian r. v. s with mean 0 and variance , then the magnitude of h follows Rayleigh distribution and the phase follows uniform distribution. Communications Engineering 35

Random process and spectra Random processes: basic concepts Ø A random process (stochastic process, or random signal) is the evolution of random variables over time. Ø A random process is a function defined over time and sample space with value at a specific time corresponding to a sample value. Ø Given , are the random variables. Ø Given , is the sample path function. Communications Engineering 36

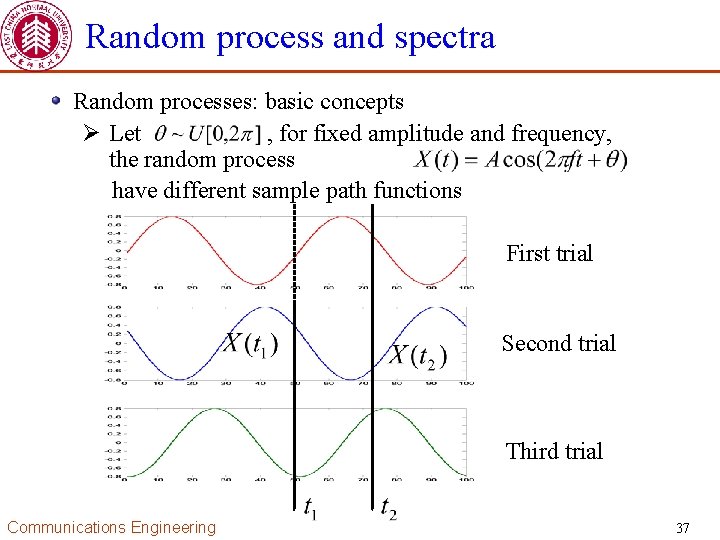
Random process and spectra Random processes: basic concepts Ø Let , for fixed amplitude and frequency, the random process have different sample path functions First trial Second trial Third trial Communications Engineering 37

Random process and spectra Random processes: basic concepts Ø The statistics of random variables at different times Ø CDF Ø Expectation function Ø Auto-correlation function Ø Covariance Communications Engineering 38

Random process and spectra Random processes: basic concepts Ø Consider for example the with , we have Ø Expectation function: Ø Auto-correlation function (assume Communications Engineering ): 39

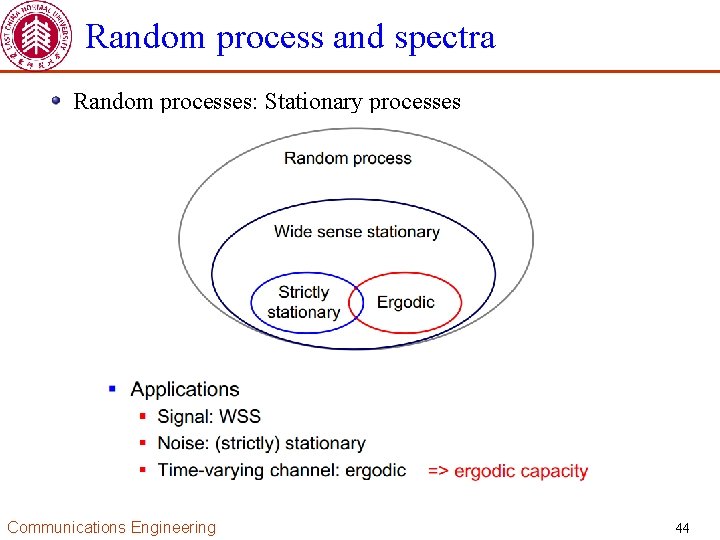
Random process and spectra Random processes: Stationary processes Ø A stochastic process is said to be stationary if for any n and The expectation function is independent of time The auto-correlation function only depends on the time difference Communications Engineering 40

Random process and spectra Random processes: Stationary processes Ø A random process is said to be Wide sense stationary (WSS) if Ø A strict stationary process satisfies for any n and Communications Engineering 41

Random process and spectra Random processes: Stationary processes Ø Some properties of WSS 1. 2. 3. 4. If , then Communications Engineering 42

Random process and spectra Random processes: Stationary processes Ø Statistical averaging Ø Time averaging Ø If time averaging = statistical averaging, then the process is said to be ergodic. (what does it mean? ) Communications Engineering 43

Random process and spectra Random processes: Stationary processes Communications Engineering 44

Random process and spectra Random processes: Stationary processes Ø Frequency domain characteristics Communications Engineering 45

Random process and spectra Random processes: Stationary processes Ø Given a deterministic signal , the power is Ø Truncate to get an energy signal Ø Parseval’s theorem Ø Hence Communications Engineering 46

Random process and spectra Random processes: Stationary processes Ø Consider as a sample path function of a random process X(t) , the average power of X(t) is Ø Power spectral density of X(t) Communications Engineering 47

Random process and spectra Random processes: Stationary processes Ø Consider a binary semi-random signal with Ø Find its power spectral density? Communications Engineering 48

Random process and spectra Random processes: Stationary processes Ø Wiener-Khinchin theorem Ø Property Communications Engineering 49

Random process and spectra Random processes: Stationary processes Ø Consider for instance the random process , we have Ø Then, Communications Engineering 50

Random process and spectra Random processes: Stationary processes Ø Given a binary random signal with Communications Engineering 51

Random process and spectra Random processes: Stationary processes Ø Then, we have Communications Engineering 52

Random process and spectra Random processes: Stationary processes Ø Random process transmission through linear systems Ø Mean of the output Communications Engineering 53

Random process and spectra Random processes: Stationary processes Ø Auto-correlation of the output Ø If the input is a WSS, then the output is also a WSS. Ø Ø PSD of the output Communications Engineering 54

Random process and spectra Random processes: Stationary processes Ø Comparison between deterministic and random signal Communications Engineering 55

Random process and spectra Random processes: Stationary processes Ø Consider for example Communications Engineering 56

Random process and spectra Random processes: Gaussian and White processes Ø Gaussian process Ø Some properties 1. If it is WSS, it is strictly stationary. 2. If the input to a linear system is a Gaussian process, the output is also a Gaussian process. Communications Engineering 57

Random process and spectra Random processes: Gaussian and White processes Ø Consider for example the noise, which is often modeled as Gaussian and stationary with zero mean Ø White noise Communications Engineering 58

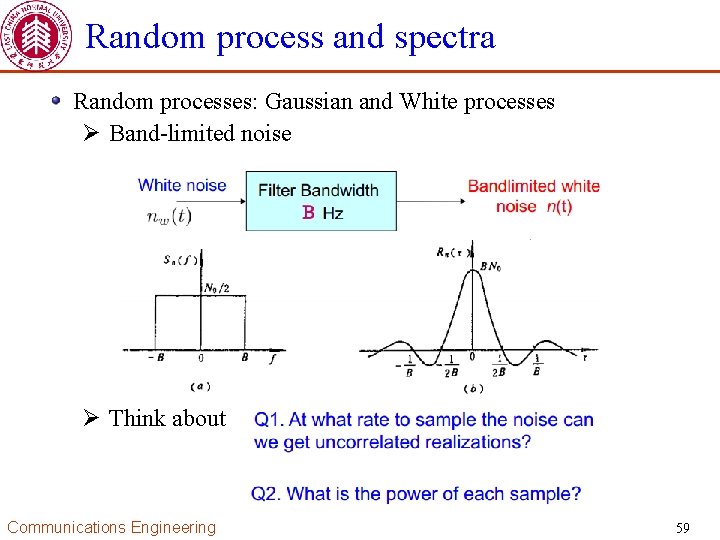
Random process and spectra Random processes: Gaussian and White processes Ø Band-limited noise Ø Think about Communications Engineering 59

Random process and spectra Random processes: Gaussian and White processes Ø Band-pass noise Ø Canonical form of a band-pass noise process Communications Engineering 60

Random process and spectra Random processes: Gaussian and White processes Ø Consider the band-pass noise. Ø If n(t) is a zero-mean, stationary and Gaussian noise, then nc(t) and ns(t) satisfy the following properties: 1. nc(t) and ns(t) are zero-mean, jointly stationary and Gaussian process. 2. Communications Engineering 61

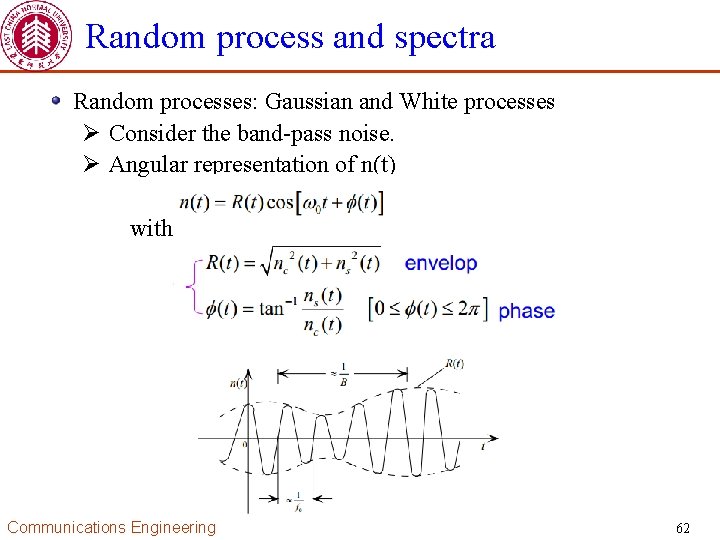
Random process and spectra Random processes: Gaussian and White processes Ø Consider the band-pass noise. Ø Angular representation of n(t) with Communications Engineering 62

Random process and spectra Random processes: Gaussian and White processes Ø Find the statistics of the envelop and phase of the angular representation of n(t). Communications Engineering 63

Random process and spectra Random processes: Gaussian and White processes Ø Overview Communications Engineering 64

Signal, random variable, random process and spectra Suggested reading & Homework Ø Chapter 2. 1 -2. 6, Chapter 5. 1 -5. 3 of the textbook Communications Engineering 65